Abstract
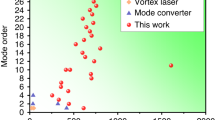
We demonstrate the generation of an intense femtosecond optical vortex (OV) pulse by employing an OV converter set between two laser amplifiers in a chirped-pulse amplification (CPA) system of a Ti:sapphire laser. The OV converter is composed of a liquid-crystal spatial light modulator (LC-SLM) exhibiting a blazed-phase computer-generated hologram, a concave mirror, and a flat mirror in the 4f setup. Owing to the intrinsic nature of the 4f setup, the OV converter is free from chromatic and topological-charge dispersions, which are always induced in a spiral phase plate conventionally used to convert an intense Gaussian laser pulse to an OV pulse, while we can avoid damage to the LC-SLM by the irradiation of a low-energy pulse before the second amplifier. We have increased the throughput of the OV converter to 42% by systematically investigating the diffraction efficiency of the blazed-phase hologram on the LC-SLM, which relaxes the gain condition required for the second amplifier. The combination of the high-throughput OV converter and the two-stage amplification enables us to generate OV pulses with an energy of 1.63 mJ and a pulse duration of 60 fs at a wavelength of ~720 nm, at which the gain of the Ti:sapphire laser is only 60% of the peak gain around 800 nm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the past few decades, optical vortices (OVs) have attracted increasing interest owing to their distinct properties of the helical phase term, \(\exp (-i \ell \phi )\), and the null center distribution, where \(\phi \) is the azimuthal angle and \(\ell \) is the topological charge [1]. The twisted wavefront of an OV suggests that it possesses a well-defined orbital angular momentum (OAM), which was verified in 1992 by Allen et al. [1]. Since the validation of the OAM in an OV, numerous promising applications [2–7] have been reported. Many studies have been carried out on monochromatic OVs, which have been widely used in the optical manipulation of molecules and nanoparticles [8–10]. More recently, scientists have been attempting to generate multichromatic OVs with high energy and ultrashort temporal profiles [11–17]. Such an OV pulse exhibits a high peak power, which is the key to inducing nonlinear phenomena such as filamentation [18], supercontinuum [19], and high-harmonic generation [20, 21]. Although the light source is important for studying these fascinating phenomena, there have so far been few experimental realizations owing to the lack of accessibility.
So far, several approaches have been adopted to generate a monochromatic OV from a TEM00 Gaussian beam, including the employment of astigmatic lenses [22], spiral phase plates [23], optical wedges [24], and computer-generated holograms (CGHs) [25, 26]. Unlike a monochromatic OV, an ultrabroadband OV should be conducted carefully to ensure that all the wavelength components are well embedded with the phase singularity. Undesirable effects such as spatial, temporal, and topological-charge dispersion are common issues arising from the above methods. To obtain a dispersion-free scheme, a variety of achromatic techniques have been proposed, for instance, employing the prism [27, 28], 2f–2f [14], and 4f configurations [13, 15] or space-variant waveplates [11, 12]. In particular, the combination of achromatic methods and laser amplifiers opens new possibilities for the generation of OVs with not only an ultrashort temporal profile but also a fairly high output energy [11, 12]. Yamane et al. have recently generated an intense OV of 1.3 mJ and a duration of 27 fs by utilizing a chirped-pulse amplification (CPA) system of a Ti:sapphire laser with a 4f OV converter comprising a liquid-crystal spatial light modulator (LC-SLM) [29]. This provides a promising means of generating an intense broadband OV with a programmably controlled topological charge. However, the output energy in their work was severely limited by the low throughput (less than several percent) of the 4f setup.
In this work, we effectively solve the limitation of the efficiency for the 4f setup and successfully generate an intense ultrashort OV by employing the combination of a lab-built two-stage CPA system and a blazed-phase hologram displayed by an LC-SLM in the 4f setup. The two-stage CPA system consists of a regenerative amplifier and a five-pass amplifier with the 4f converter placed between them. To precisely control the phase modulation of the LC-SLM in the 4f setup, we carefully calibrate the LC-SLM by determining the phase value with respect to the pixel level. Employing the calibrated relationship, we further investigate the throughput of the 4f setup with different numbers of phase steps in the blazed-phase hologram. The measurement shows that a throughput of up to 42% can be obtained for the 4f system in the case of 10 phase steps, which is considerably higher than the previous result [29]. The improved efficiency enables the generation of a 75 μJ OV seed pulse for the second multipass amplifier. Owing to the high throughput of the OV converter, only five passes are sufficient to efficiently extract the energy from the second amplifier even though the wavelength of the OV seed pulse is much shorter than 800 nm. Through the second-stage amplification and chirp compensation, we finally obtain OVs with energy of up to 1.63 mJ and a duration of 60 fs. To the best of our knowledge, the presented result is the largest energy ever reported in ultrashort singular optics generated using a 4f OV converter. It is expected that such a light source can provide new prospects in high-intensity-field physics, as we have already demonstrated in Ref. [30].
2 Front end of the CPA system
The concept of our experimental configuration is based on the work by Yamane et al. [29], in which a 4f OV converter was positioned between two Ti:sapphire-based amplifiers. Figure 1 depicts our experimental setup. Initial pulses were generated by a Ti:sapphire oscillator (Rainbow, Femtolasers–Spectra-Physics) with an average power of 280 mW, a repetition rate of 78 MHz, and a duration of less than 10 fs. The wavelength of the oscillator ranges from 650 to 1030 nm. We added a positive chirp to the output pulse from the oscillator to increase the pulse duration to \(\sim 300\) ps using an Öffner stretcher. The central wavelength of the output beam from the Öffner stretcher was tuned to approximately 720 nm, and the spectral width was limited to \(\sim 80~\hbox {nm}\). This wavelength range was designed for an application other than the generation of OV pulses. After the stretcher, the pulse was amplified by a lab-built first-stage Ti:sapphire regenerative amplifier pumped by the second-harmonic pulse of a diode-pumped Nd:YLF laser (Darwin, Quantronix-Continuum) with an energy of 5.36 mJ at a repetition rate of 200 Hz. The output of the regenerative amplifier was sent to a pulse slicer consisting of a pair of crossed polarizers and a Pockel’s cell set between them to isolate the regenerative amplifier from the following multipass amplifier. The pulse energy behind the pulse slicer was measured to be 200 μJ.
(Color online) a Setup for the calibration of the phase modulation. b Phase modulation, \(\varPhi \), for various wavelengths as a function of the input pixel level. The measurements are in good agreement with the fitting curve \(\varPhi =0.027V\pm 0.1\). The spectrum of the light pulse is shown in the inset
3 Mode conversion
After the first amplification, we injected the light pulse into the 4f OV converter with nearly normal incidence (\(\theta \sim 1.5^{\circ }\)), as depicted in Fig. 1. The 4f setup is composed of a concave mirror C1, flat mirrors, and an LC-SLM (Hamamatsu Photonics X10468-01, \(600\times 792\) pixels) as the key device for the mode conversion from a Gaussian to an OV. The light beam impacts on the LC-SLM twice during the transformation, as shown in the inset of Fig. 1. The input beam is first converted into the OV by a forklike blazed-phase grating [15, 26] in the upper part of the LC-SLM and then Fourier transformed using concave mirror C1 with a curvature of 1 m. Flat mirror M1 was placed at the focal plane of C1 and an aperture was set in front of M1 to selectively transmit the first-order diffraction light. The beam was then reflected back to the blazed-phase grating without a forklike pattern in the lower part of the LC-SLM to compensate the angular dispersion caused by the upper part. Note that the incident beam to the 4f system was magnified in advance to ~3 mm at the 1/e2 level to prevent damage to the LC-SLM. The phase describing the blazed grating with a spiral phase modulation, \(\varPhi \), which was projected onto the xy plane of the LC-SLM, can be written as [15, 26]
where \({\text {mod}}(a, b)=a-b\,\, {\text {Int}}(a/b)\) is the modulus function, \(\varLambda =(DS)/600\) is the period of the grating, \(D=10\) mm is the width of the grating, S is the number of phase steps in a period, and 600 is the number of pixels. The Cartesian coordinates (x, y) on the LC-SLM are transformed to cylindrical coordinates \((r=\sqrt{x^2+y^2},\phi =\arctan (y/x))\). An example of a blazed-phase grating with 10 steps is illustrated in Fig. 2, where Fig. 2a shows the forklike blazed-phase grating, and Fig. 2b shows the phase distribution corresponding to the red line marked in Fig. 2a. \(\delta \varPhi \) is the phase difference between the waves in two neighboring levels. Each phase modulation level \(\varPhi \) is controlled by the spatial variation of the refractive index \(n(r,\phi )\) of the liquid-crystal (LC) layer in the LC-SLM. \(n(r, \phi )\) is adjusted to obtain the desired phase profile for the LC layer with a fixed thickness, T, by applying a voltage to it. The voltage is determined by the input pixel value, which ranges from 0 to 255. In addition, the variation of the incident angle of the light also changes the phase profile. The light beam diffracted by the blazed-phase structure with incident angle \(\theta \) and difference \(\delta n\) between the refractive indices of two neighboring levels is schematically depicted in Fig. 3, where W is the width of a pixel. \(\delta \varPhi \) can be obtained geometrically by calculating the difference between the optical paths, \(2a_2+b_2-(2a_1+b_1)\), of the two rays and is obtained as \(\delta \varPhi =(2\pi /\lambda ) [2T n_1\delta n/(n_1^2-\sin ^2\theta )^{1/2}]\), where we have neglected \(\delta n^2\) by assuming a large number of levels in a grating period, and \(\lambda \) is the wavelength of the incident light. For normal incidence with \(\theta =0\), the phase difference is simplified to \(\delta \varPhi =(2\pi /\lambda )2T\delta n\). We conducted the experiment with the scheme having nearly normal incidence, in which the effect of \(\theta \) can be neglected.
To generate predictable pulse shapes, the relationship between \(\varPhi \) and the input pixel value should be carefully calibrated in advance. Figure 4a depicts the setup used to determine \(\varPhi \) by measuring the intensity modulation by the LC-SLM. The LC molecules in the LC-SLM were horizontally aligned, and the polarization of the incident light beam was adjusted to \(45^{\circ }\) to the molecules. The incident angle of the light was aligned to nearly normal to the surface of the LC layer. The LC-SLM introduced a phase shift \(\varPhi \) for only the horizontal component of the incident light and then reflected it back through the \(\lambda \)/2-plate and the polarizer, as shown in Fig. 4a. The resultant intensity of the horizontal component can be expressed as
where \(I_{\text {max}}\) and \(I_{\text {min}}\) are the maximum and minimum light intensity, respectively. The setup measures the intensity variation within 256 pixel levels. Therefore, Eq. (2) can be used to calculate the relationship between \(\varPhi \) and the input pixel level, as illustrated in Fig. 4b. Here, we focus on the range between 700 and 740 nm, corresponding to the bandwidth of the measured spectrum of the incident beam, as shown in the inset of Fig. 4b. The curves scarcely change with the wavelength and can be fitted with the relationship \(\varPhi =0.027\,V\pm 0.1\) rad, where V is the pixel level. The maximum phase modulation is adjusted to 2.19\(\pi \pm 0.1\) rad; thus, the phase resolution is \(0.0086\pi \pm 0.0004\)/digit. The calibration enables us to precisely control the phase value \(\varPhi \) by assigning the correct pixel level, which is important for producing an OV with high throughput via the 4f system.
Figure 5a shows measured and theoretical values of the efficiency in the case of first-order diffraction light through the 4f system with various numbers of phase steps, S. The efficiency is defined as the first-order diffraction intensity divided by the incident light intensity and can be analytically expressed as [31]
where \(\Delta =(S-1)\delta \varPhi /2\pi \) is the total change in the phase depth in a period. \(\eta \) represents the efficiency of the first-order diffraction obtained after the light beam is reflected once by the blazed-phase grating. Note that \(\eta \) can be changed by varying the incident angle, \(\theta \), since \(\delta \varPhi \) of \(\Delta \) is a function of \(\theta \), as we mentioned previously. Here, we use the same incident angle as that for the calibration setup in Fig. 4a. Therefore, we are able to use the fitting result \(\varPhi =0.027V\pm 0.1\) to obtain \(\delta \varPhi \) for the determination of \(\Delta \) in \(\eta \). \(\Delta \) is given by \(\Delta =1\pm [0.1(S-1)/\pi ]\) for \(\delta \varPhi =[2\pi /(S-1)]\pm 0.2\), where \(\pm 0.2\) originates from the phase calibration error. Through the 4f converter, the simulated efficiency in Fig. 5a is thus obtained by considering the phase calibration error, the utilization efficiency of the LC-SLM of 79.2%, and the average reflectivity of the mirrors of 98%, i.e., \((\eta \times 0.792)^2\times 0.98^5\). It is shown in Fig. 5a that the efficiency increases with increasing number of phase steps. The experimental results show good agreement with the simulation. We are able to obtain high throughput exceeding 40% by applying 10 steps, as shown in Fig. 5a. Figure 5b illustrates the Fourier-transformed patterns from the blazed-phase grating. It is clearly shown that the light intensity of the first-order diffraction increases with increasing number of phase steps and dominates the total intensity distribution when the number of phase steps reaches five. Moreover, the spacing of each order of the diffraction light decreases with increasing number of phase steps owing to the increase in the grating period, \(\varLambda \).
4 Second-stage amplification and pulse compression
In the following experiment, we used 10 phase steps as an example to generate OV pulses. The throughput of the 4f setup was obtained to be 42% for 10 steps, as shown in Fig. 5a. The first-order diffraction light from the 4f system was then collimated with a 4/5 telescope composed of two convex lenses for mode matching to the following five-pass amplifier, as shown in Fig. 1. The incident angle to the convex lenses should be carefully adjusted to reduce the astigmatism in the output beam from the telescope. In this stage, the pulse energy of the resultant OV was measured to be 75 and 72 μJ for \(\ell =1\) and \(\ell =2\), respectively. The pulse energy was then amplified to 3.73 and 3.1 mJ for \(\ell =1\) and \(\ell =2\), respectively, through the five-pass amplifier pumped with an energy of 12.7 mJ. Thus, the energy extraction efficiency was 29.3 and 24.4% for \(\ell =1\) and \(\ell =2\), respectively. The high efficiency at the wavelength of ~720 nm, at which the gain of the Ti:sapphire laser is reduced to approximately 60% of the peak gain around 800 nm, is due to the fact that the careful calibration of the 4f system in the previous stage enables the generation of a 100-μJ-level seeding OV pulse to the multipass amplifier. Figure 6 depicts the experimental evolution of the pulse energy for \(\ell =0, \ell =1\), and \(\ell =2\) with respect to the number of passes in the five-pass amplifier. It is shown that the efficiency of the five-pass amplifier for \(\ell =1\) is comparable to that for \(\ell =0\). The efficiency for \(\ell =2\), which has a larger beam profile than the \(\ell =1\), is slightly lower since the mode-matching condition between the pump beam and the seed deteriorates.
In the final procedure for chirp compensation, the beam size of the output OV from the five-pass amplifier was first magnified by a 5/1 telescope to avoid the damaging the following grating-pair (2000 lines/mm) compressor, which had a damage threshold of \(100\hbox { mJ/cm}^2\). The OV pulses of \(\ell =1\) and \(\ell =2\) were then compensated for frequency chirp by the compressor, and the outputs were obtained to be 1.63 and 1.35 mJ, respectively. The low throughput (\(\sim 43.6\%\)) of the grating-pair compressor is due to the degradation of the gold coating on the gratings with prolonged use. The spectrum of the output pulses from the compressor was also measured by a calibrated spectrometer (Ocean Optics, USB2000), as shown in Fig. 7a. The measured spectrum is slightly redshifted during the five-pass amplification, resulting in the central wavelength shifting from 715 to 722 nm. The spectral width is ~14 nm (FWHM). We measured the autocorrelation trace of the pulse using a single-shot autocorrelator set behind the compressor. The measured trace is depicted as circles in Fig. 7b and is in good agreement with the autocorrelation trace calculated from the Fourier limit pulse of the measured spectrum, as shown in Fig. 7b. Thus, we conclude that the pulse behind the compressor is near the Fourier limit and has a pulse duration of ~60 fs.
(Color online) a Measured spectra for the light pulses before and after five-pass amplification. b Fourier limit pulse (filled curve) and autocorrelation of the Fourier limit pulse (solid line) calculated from the spectrum in (a). The autocorrelation trace measured using a single-shot autocorrelator is also shown (circles). FL Fourier limit, AC autocorrelation
(Color online) Determination of the topological charge for the OV using a cylindrical lens. a Experimental scheme for the beam transformation via the cylindrical lens. b, d, and f Beam profiles for \(\ell =0, \ell =1\), and \(\ell =2\), respectively. Their corresponding Fourier-transformed patterns at the focal plane of the cylindrical lens are shown in (c), (e), and (g), respectively
Furthermore, Fig. 8b, d, and f displays the beam profiles for \(\ell =0, \ell =1\), and \(\ell =2\), respectively. To confirm the topological charge, we adopted the astigmatic transformation, which is a simple technique commonly used for determining \(\ell \) for multichromatic OVs [32]. In the technique, the OVs are converted through a cylindrical lens with a focal length of \(f_{\text {cyl}}\) to obtain their Fourier-transformed images at the focal plane of the cylindrical lens (\(z=f_{\text {cyl}}\)), as schematically illustrated in Fig. 8a. The resultant pattern of the OV features tilted dark stripes and their number indicates the modulus of the topological charge, \(|\ell |\). Using this method, we verify the topological charges for the generated OV pulses, as shown in Fig. 8c, e, and g. Though it is sufficient to determine the topological charge using a cylindrical lens [32], one more cylindrical lens can also be employed to compensate the astigmatism induced by the first cylindrical lens to generate a well-defined Hermite–Gaussian mode [33]. Thus, the topological charge of the OV can be clearly determined using the relations \(\ell =m-n\), and \(p=\text {min}(m,n)\), where m and n are the transverse indices of the Hermite–Gaussian mode and p is the radial index of the OV [33].
5 Conclusions
We experimentally generated intense ultrashort OV pulses with energy up to 1.63 mJ and a pulse duration of 60 fs in the near-infrared region by employing a 4f OV converter placed between two amplifiers in a CPA system of a Ti:sapphire laser. To obtain a high throughput for the 4f converter, we systematically calibrated the phase modulation, \(\varPhi \), for the LC-SLM in the 4f setup to find the value of \(\varPhi \) as a function of the pixel level, V. The careful calibration enabled us to precisely determine \(\varPhi \) by designating the corresponding V. Using the relationship between \(\varPhi \) and V, we displayed the blazed-phase gratings on the LC-SLM to investigate the throughput of the 4f setup with various numbers of phase steps, S. For S = 10, we were able to obtain a reasonably high throughput of up to 42% for the 4f system. The preamplification and the improved efficiency of the 4f setup led to the generation of a 100-μJ-level OV, which
enabled us to extract the pulse energy from the second multipass amplifier with an efficiency of 29.3%. Finally, we utilized a cylindrical lens to clarify the topological charge of the generated OVs. It is considered that the light source will be useful for the study of nonlinear singular optics.
References
L. Allen, M.W. Beijersbergen, R.J.C. Spreeuw, J.P. Woerdman, Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, 8185 (1992)
M.S. Soskin, M.V. Vasnetsov, Singular optics. Prog. Opt. 42, 219 (2001)
K. Toyoda, F. Takahashi, S. Takizawa, Y. Tokizane, K. Miyamoto, R. Morita, T. Omatsu, Transfer of light helicity to nanostructures. Phys. Rev. Lett. 110, 143603 (2013)
A. Mair, A. Vaziri, G. Weihs, A. Zeilinger, Entanglement of the orbital angular momentum states of photons. Nature 412, 313 (2001)
J. Wang, J.-Y. Yang, I.M. Fazal, N. Ahmed, Y. Yan, H. Huang, Y. Ren, Y. Yue, S. Dolinar, M. Tur, A.E. Willner, Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 6, 488 (2012)
K.I. Willig, S.O. Rizzoli, V. Westphal, R. Jahn, S.W. Hell, STED microscopy reveals that synaptotagmin remains clustered after synaptic vesicle exocytosis. Nature 440, 935 (2006)
H. He, M.E.J. Friese, N.R. Heckenberg, H. Rubinsztein-Dunlop, Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett. 75, 826 (1995)
K.T. Gahagan, G.A. Swartzlander Jr., Optical vortex trapping of particles. Opt. Lett. 21, 827 (1996)
N.B. Simpson, K. Dholakia, L. Allen, M.J. Padgett, Mechanical equivalence of spin and orbital angular momentum of light: an optical spanner. Opt. Lett. 22, 52 (1997)
H. Adachi, S. Akahoshi, K. Miyakawa, Orbital motion of spherical microparticles trapped in diffraction patterns of circularly polarized light. Phys. Rev. A 75, 063409 (2007)
Y. Tokizane, K. Oka, R. Morita, Supercontinuum optical vortex pulse generation without spatial or topological-charge dispersion. Opt. Express 17, 14517 (2009)
K. Yamane, Y. Toda, R. Morita, Ultrashort optical-vortex pulse generation in few-cycle regime. Opt. Express 20, 18986 (2012)
K. Bezuhanov, A. Dreishuh, G.G. Paulus, M.G. Schätzel, H. Walther, Vortices in femtosecond laser fields. Opt. Lett. 29, 1942 (2004)
I.G. Mariyenko, J. Strohaber, C.J.G.J. Uiterwaal, Creation of optical vortices in femtosecond pulses. Opt. Express 13, 7599 (2005)
I. Zeylikovich, H.I. Sztul, V. Kartazaev, T. Le, R.R. Alfano, Ultrashort Laguerre-Gaussian pulses with angular and group velocity dispersion compensation. Opt. Lett. 32, 2025 (2007)
V.G. Shvedov, C. Hnatovsky, W. Krolikowski, A.V. Rode, Efficient beam converter for the generation of high-power femtosecond vortices. Opt. Lett. 35, 2660 (2010)
M. Bock, S.K. Das, C. Fischer, M. Diehl, P. Börner, R. Grunwald, Reconfigurable wavefront sensor for ultrashort pulses. Opt. Lett. 37, 1154 (2012)
P. Polynkin, C. Ament, J.V. Moloney, Self-focusing of ultraintense femtosecond optical vortices in air. Phys. Rev. Lett. 111, 023901 (2013)
D.N. Neshev, A. Dreischuh, G. Maleshkov, M. Samoc, Y.S. Kivshar, Supercontinuum generation with optical vortices. Opt. Express 18, 18368 (2010)
G. Gariepy, J. Leach, K.T. Kim, T.J. Hammond, E. Frumker, R.W. Boyd, P.B. Corkum, Creating high-harmonic beams with controlled orbital angular momentum. Phys. Rev. Lett. 113, 153901 (2014)
R. Géneaux, A. Camper, T. Auguste, O. Gobert, J. Caillat, R. Taïeb, T. Ruchon, Synthesis and characterization of attosecond light vortices in the extreme ultraviolet. Nat. Commun. 7, 12583 (2016). doi:10.1038/ncomms12583
M.W. Beijersbergen, L. Allen, H. Vanderveen, J.P. Woerdman, Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 96, 123 (1993)
M.W. Beijersbergen, R.P.C. Coerwinkel, M. Kristensen, J.P. Woerdman, Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 112, 321 (1994)
Y. Izdebskaya, V. Shvedov, A. Volyar, Generation of higher-order optical vortices by a dielectric wedge. Opt. Lett. 30, 2472 (2005)
N.R. Heckenberg, R. McDuff, C.P. Smith, A.G. White, Generation of optical phase singularities by computer-generated holograms. Opt. Lett. 17, 221 (1992)
J. Arlt, K. Dholakia, L. Allen, M.J. Padgett, The production of multiringed Laguerre-Gaussian modes by computer-generated holograms. J. Mod. Opt. 45, 1231 (1998)
A. Schwarz, W. Rudolph, Dispersion-compensating beam shaper for femtosecond optical vortex beams. Opt. Lett. 33, 2970 (2008)
A.J. Wright, J.M. Girkin, G.M. Gibson, J. Leach, M.J. Padgett, Transfer of orbital angular momentum from a super-continuum, white-light beam. Opt. Express 16, 9495 (2008)
K. Yamane, A. Honda, Y. Toda, R. Morita, Over 1-mJ intense ultrashort optical-vortex pulse generation with programmable topological-charge control by chirped-pulse amplification, Ultrafast Phenomena XIX. Springer International Publishing (2015)
Y.-C. Lin, Y. Nabekawa, K. Midorikawa, Conical third-harmonic generation of optical vortex through ultrashort laser filamentation in air. Opt. Express 24, 14857 (2016)
G. J. Swanson, Binary optics technology: the theory and design of multi-level diffractive optical elements, No. TR-854. Massachusetts Inst. Tech. Lexington Lincoln Lab (1989)
V. Denisenko, V. Shvedov, A.S. Desyatnikov, D.N. Neshev, W. Krolikowski, A. Volyar, M. Soskin, Y.S. Kivshar, Determination of topological charges of polychromatic optical vortices. Opt. Express 17, 23374 (2009)
J. Courtial, M.J. Padgett, Performance of a cylindrical lens mode converter for producing Laguerre-Gaussian laser modes. Opt. Commun. 159, 13 (1999)
Acknowledgements
We thank Dr. K. Isobe for providing the spatial light modulator and Dr. K. Yamane for the useful discussion on the amplification of OVs. This work was financially supported by the Advanced Photon Science Alliance commissioned by MEXT and partly contributed to the objectives of CREST studies commissioned by JST. Y. N. and K. M. gratefully acknowledge the financial support from Grant-in-Aid for Scientific Research (A) No. 26247068 and Grant-in-Aid for Scientific Research (S) 26220606 from MEXT, Japan.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lin, YC., Nabekawa, Y. & Midorikawa, K. Generation of intense femtosecond optical vortex pulses with blazed-phase grating in chirped-pulse amplification system of Ti:sapphire laser. Appl. Phys. B 122, 280 (2016). https://doi.org/10.1007/s00340-016-6557-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00340-016-6557-y