Optimized weak measurement for spatial spin-dependent shifts at Brewster angle

Abstract

As Brewster law goes, the polarization selectivity when a light beam reflected at Brewster angle is feasible. We find that this polarization selectivity is still effective incorporated with weak measurement. So we realize an optimized weak measurement technique without preselection polarizer. This scheme is exploited to observe the spatial spin-dependent shifts when a linearly polarized beam is reflected at Brewster angle. The theoretical and experimental results show that by changing the polarization orientation of incident beam, the in-plane spin-dependent shift direction can be reversed, while the out-of-plane spin-dependent shift direction keeps unchanged. Our results may enrich the application of weak measurement.

1 Introduction

According to geometric optics, the incident and reflected beams meet at one point upon the interface between two media. However, in physical optics, a bounded light beam actually experiences a different reflection behavior from that prediction in geometric optics. For a beam with definite diameter, it has been extensively identified that in-plane and out-of-plane (namely, perpendicular to the incident plane) shifts occur in the interaction of light with interface. The in-plane shift in total internal reflection is initially presented as the Goos–Hänchen (GH) shift [1]. The out-of-plane one is also well known as Imbert–Fedorov (IF) shift [2], which performs as the out-of-plane spin-dependent shift (SDS) of the barycenter of circularly polarized beam. Based on the IF shift, an intriguing dynamic behavior, the separation of right-handed (RH) and left-handed (LH) circularly polarized components of the incident beam, can be observed for a linearly polarized beam with bounded width [3, 4]. This phenomenon can be considered as a photonic analog of the electric spin Hall effect occurring in solid-state systems, generally named spin Hall effect of light (SHEL) [5, 6]. Furthermore, these two kinds of shifts can be presented in spatial and angular domains (see, e.g., [7] and the references therein for a review).

More generally, the magnitude of the SDSs is only on the nanoscale and is hard to achieve accurate measurement. In 2008, Hosten et al. firstly introduced the weak measurement technique to precisely characterize the tiny out-of-plane SDS associated with SHEL [5, 8]. This unique method allows significant magnification of beam shifts and paves a useful way to observe this SDS and GH shift in optical reflection [9–15] and identify the polarization chirality of light beam [16]. In principle, this weak measurement technique employs two appropriate pre- and post-selection states to achieve an enhancement shift. In considerable amount of measurements, the pre- and post-selection processes are implemented by using two nearly crossed Glan–Taylor polarizers (GTPs) [5–7, 9–12], of which we can choose the optimal pre- and post-selection to acquire the maximum weak value [17]. Nevertheless, Kong et al. present an effective solution consisting of two polarizers with an angle of 45$^{\circ }$ to measure the SHEL around the Brewster angle [18, 19]. In the past few years, it has aroused considerable amount of investigations to manipulate the magnitude and direction of spin splitting [19–24] and drive the development of other effective measurement techniques, such as, lock-in amplifier [25], interferometry [26, 27]. Particularly, due to the special reflection and refraction properties at Brewster angle, the performance of out-of-plane and in-plane SDS around Brewster angle has attracted lots of attention [18–20, 22, 23]. However, most of these techniques just deal with SHEL around the Brewster angle for horizontally or vertically polarized incident beam. Most recently, Qiu et al. reported a large in-plane spin-dependent splitting at Brewster angle and demonstrated that the spin-dependent splitting direction can be switched by slightly adjusting the polarization orientation of the incident beam [19].

Our work combines the weak measurement technique with the polarization selectivity of Brewster angle incidence, which converts a linearly polarized incident beam into a vertically polarized beam after reflection [28]. Thus, the Brewster angle incidence can be viewed as the role of preselection in weak measurement technique. Under this scheme, we experimentally realize the optimized weak measurement for characterizing the out-of-plane and in-plane SDSs by using one almost horizontally polarized post-selection GTP. In such a case, the out-of-plane and in-plane SDSs almost have identical magnitude and can be manipulated separately. Additionally, the in-plane SDS direction can be switched by adjusting the polarization angle of the incident beam.

2 Theory analysis

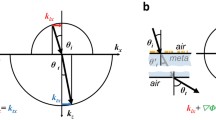
Here, we suppose that a linearly polarized Gaussian beam impinges upon the air–glass interface and is reflected, as illustrated in Fig. 1a. A Cartesian coordinate system (x, y, z) is attached to the air–glass interface ($z =0$), where $z <0$ denotes the air space and $z >0$ signifies the glass side. Two Cartesian coordinate systems ($x _i$, y, $z _i$) and ($x _r$, y, $z _r$) are aligned with the incident and reflected beams, respectively. The transverse electric field of incident Gaussian beam propagating along $z _i$-axes can be expressed as

$$\begin{aligned} {\mathbf {E}}_i=E_{ix}{\mathbf {e}}_{ix}+E_{iy}{\mathbf {e}}_{iy}. \end{aligned}$$

(1)

where ${\mathbf {e}}_{ix}$ and ${\mathbf {e}}_{iy}$ denote the unit vectors along $x_i$ and y-axes, respectively; $E_{ix}=E_i \cos \gamma _i$, $E_{iy}=E_i\sin \gamma _i$, $\gamma _i$ denotes the polarization angle, which is defined as the angle between the electric field vector $\mathbf{E }_i$ and $x_i$ axes as shown in Fig. 1a; thus, ${\mathbf {e}}_{ix}$ and ${\mathbf {e}}_{iy}$ also, respectively, correspond to the p-, s-polarization states; the amplitude $E_{i}= C \alpha \mathrm{exp}[\beta (x _i^2 + y ^2)]$, with C is the constant electric field amplitude, $\alpha = \omega _0\mathrm{exp}[i(k _iz _i-\tan ^{-1}(z _i/z _0))]/\omega (z _i)$, $\beta = 1/\omega (z _i)+ik _i/[2\hbox {R}(z _i)]$; $\omega (z _i)=\omega _0[1+(z _i/z _0)^2]^{1/2}$ is the beam radius; $\hbox {R}(z _i)=z _i[1+(z _0/z _i)^2]$ is the radius curvature of the wave front; $\omega _0$ is the waist radius of the Gaussian beam; $z _0=k _i\omega _0^2/2$ is the Rayleigh length, and $k _i=2\pi /\lambda$ is the wave number with $\lambda$ being the wavelength of light in vacuum.

Fig. 1

a Schematic illustration of a bounded beam reflected at air–glass interface. The incident beam (green) spits into RH (red) and LH (blue) circularly polarized components, both of which perform in-plane ($\delta _x$) and out-of-plane ($\delta _y$) SDSs. b The side view of (a) shows the in-plane SDSs occurring along $x_r$ axes. c The top view of (a) illustrates the out-of-plane SDSs occurring along y-axes

The incident Gaussian beam with bounded width can be viewed as a wave packet containing a series of plane wave components, each of which has different propagation direction and incident angle. Hence, in our calculation, we first decompose the incident beam into plane wave components. After Fourier transform, the angular spectrum of the incident beam can be written as

$$\begin{aligned} {\tilde{E}}_i=\frac{C \alpha }{2\beta }\mathrm{exp}\left[ -\left( k _{ix }^2+k _{iy }^2\right) \big /4\beta \right] . \end{aligned}$$

(2)

We then apply accurate Fresnel coefficients to each plane wave component and obtain the reflected angular spectra. Via inverse Fourier transform, the complex amplitude of the reflected beam, can be expressed as $E _r(x_r, y_r, z_r) = \int \int \tilde{E}_r(k _{rx}, k _{ry}) \exp [i(k _{rx}{} x _r)+k _{ry}{} y _r)+ k _{rz}{} z _r)] \hbox {d}{} k _{rx}\hbox {d}{} k _{ry}$, where $\tilde{E}_r(k _{rx}, k _{ry})$ is the reflected angular spectrum, $k _{rz}=[k _r^2-(k _{rx}^2+k _{ry}^2)]^{1/2}$ is the longitudinal wave vector. By means of the boundary condition of electric field distribution, we can obtain the angular spectrum of reflected beam [29]

$$\begin{aligned} \left[ \begin{array}{cc} \tilde{E}_{rx}\\ \tilde{E}_{ry} \end{array}\right] =\left[ \begin{array}{cccc} r_p&{}\frac{k_{ry}(r_p+r_s)\mathrm{cot}\theta _i}{k_0}\\ -\frac{k_{ry}(r_p+r_s)\mathrm{cot}\theta _i}{k_0}&{}r_s \end{array}\right] \left[ \begin{array}{cc} \tilde{E}_{ix}\\ \tilde{E}_{iy} \end{array}\right] . \end{aligned}$$

(3)

where $r _p$ and $r _s$ are the Fresnel coefficients of horizontal and vertical polarizations, respectively. In (3), according to the transverse boundary condition, the transverse wave vectors have relations as: $k _{ix}=-k _{rx}$ and $k _{iy}= k _{ry} = k _y$. Note that, for a bounded width incident wave packet, different angular spectra experience varied rotation to satisfy the transverse boundary condition. Hence, the Fresnel reflection coefficients $r_p$ and $r_s$ in (3) should be expanded as Taylor series around the central wave vector, and their first-order approximation can be expressed as: $r _{p/s} = r _{p/s}(\theta _i) + (\partial r _p/\partial r _s)k _{ix}/k _i$.

Next, we suppose that a linearly polarized Gaussian beam with arbitrary polarization orientation is reflected. According to (2) and (3), as well as the inverse Fourier transform, we can obtain the reflected field consisting of two orthogonal polarization components. Furthermore, to intuitively present the SDSs, according to the relationship between linear polarization basis states ($|{\mathbf {e}}_x\rangle$ and $|{\mathbf {e}}_y\rangle$) and spin basis states: $|+ \rangle = (|{\mathbf {e}}_x + i|{\mathbf {e}}_y)/\sqrt{2}$ and $|-\rangle = (|{\mathbf {e}}_x- i|{\mathbf {e}}_y)/\sqrt{2}$, ($| + \rangle$ and $| - \rangle,$ respectively, correspond to RH and LH circular polarizations), we transform the reflected field into the expression of two opposite spin components, which can be expressed as

$$\begin{aligned} E_{r|\pm \rangle }&=\frac{C }{\sqrt{2}\alpha ^{\prime }}\left( {\mathbf {e}}_{rx}\pm{\mathrm{i}}{\mathbf {e}}_{ry}\right) {\mathrm{exp}}\left[ -\beta ^{\prime }\left( x _r^2+y _r^2\right) \right] \\ &\quad\left[ c {} r _p\mp {\mathrm{i}}{} s {} r _s\mp \frac{x _r}{z _R+{\mathrm{i}}{} z _r}\left( s \frac{\partial r _s}{\partial \theta _i}\pm {\mathrm{i}}{} c \frac{\partial r _p}{\partial \theta _i}\right) \right. \\ &\quad\left. \mp \frac{y _r}{z _R+{\mathrm{i}}{} z _r}(r _p+r _s){\mathrm{cot}}\theta _i(c \mp {\mathrm{i}}{} s )\right] . \end{aligned}$$

(4)

where the shorthands $c = \cos \gamma _r$ and $s = \sin \gamma _r$, ${\mathbf {e}}_{rx}$ and ${\mathbf {e}}_{ry}$ denote the unit vectors along $x _r$ and y-axes, respectively, $\gamma _r$ is the polarization angle of the reflected beam with $\mathrm{cos}\gamma _r = r _p\mathrm{cos}\gamma _i/(r _p^2 \mathrm{cos}\gamma _i^2 + r _s^2 \mathrm{sin}\gamma _i^2)^{1/2}$ and $\mathrm{sin}\gamma _r = r _s \mathrm{sin}\gamma _i/(r _p^2 \mathrm{cos}\gamma _i^2 + r _s^2 \mathrm{sin}\gamma _i^2)^{1/2}$ (caused by the difference between the reflection of p- and s-polarizations), $\alpha ^{\prime }= \omega _0\mathrm{exp}[i(k _rz _r-\mathrm{tan}^{-1}(z_r/z_0))]/\omega (z_r), \beta ^{\prime }=1/\omega (z _r)+ik _r/[2R(z _r)]$.

According to (4), it is clear that the RH and LH circular polarizations composing the reflected beam have the same intensity, and the intensity distributions are closely related not only to the incident angle $\theta _i$ but also to the polarization angle $\gamma _i$. However, it is difficult to draw a visible conclusion about the spatial shifts of spin components with the closed-form expression. For further exploring this relationship, we compare the intensity barycenter of spin components, which can be expressed as

$$\begin{aligned} \delta _{x(y)|\pm \rangle }=\frac{\int \int A {} I _{r|\pm \rangle }(x _r, y _r, z _r)dx _rdy _r}{\int \int I _{r|\pm \rangle }(x _r, y _r, z _r)dx _rdy _r}. \end{aligned}$$

(5)

where $A = x _r$ and y, $\delta _x$ and $\delta _y$ separately denote the in-plane SDS along $x _r$ axes (as shown in Fig. 1b) and the out-of-plane SDS along y-axes (as shown in Fig. 1c), $I _r(x _r$, $y _r$, $z _r)\propto {\mathbf {p}}_r\cdot {\mathbf {e}}_{rz}$ is the intensity of reflected spin components, ${\mathbf {p}}_r\propto \hbox {Re}({\mathbf {E}}_r\times {\mathbf {H}}_r^*)$ is the linear momentum density with ${\mathbf {H}}_r=-ik _r^{-1}\nabla \times {\mathbf {E}}_r$. It is worthy noting that the spatial and angular SDSs for the whole beam and its polarization components in three different bases have been discussed explicitly in [30]. The experimental scheme described in the next only responses to the linear shifts in the position space [5, 9, 31], i.e., spatial shifts. Hence, the angular shifts in the momentum space do not be presented here.

From (4) to (5), it is evident that the SDSs are dependent on the incident angle $\theta _i$ and the polarization angle $\gamma _i$. Here, we focus on the Brewster incident situation, i.e., $\theta _i=\theta _B$. Based on (4) and (5), the out-of-plane and in-plane SDSs can thus be separately expressed as

$$\begin{aligned} \delta _{x|\pm \rangle }= & {} \pm \mathrm{sin}\gamma _r\mathrm{cos} \gamma _r[1-r_s/r_s(\theta _B)]/k _{ix}, \end{aligned}$$

(6)

$$\begin{aligned} \delta _{y|\pm \rangle }= & {} \mp \mathrm{sin} \gamma _r^2\mathrm{cot}\theta _B/k _{i}. \end{aligned}$$

(7)

Note that the out-of-plane and in-plane SDSs are both closely dependent on the polarization angle $\gamma _i$ for a fixed incident angle. This provides a convenient way to manipulate the out-of-plane and in-plane SDSs, by altering the incident polarization angle $\gamma _i$. In addition, as discussed above, the incident beam with elliptical polarization can also be decomposed into the p- and s-polarized components, then deduce the reflected field, and obtain the reflected field represented by two circularly polarized basis states, as shown in (4).

3 Optimized weak measurement scheme

According to Brewster law, for an arbitrarily linearly polarized beam incident at $\theta _B$, the reflected beam only includes the s-polarized component, so the reflection process naturally acts on the role of preselection. This means that the preselection GTP in weak measurement can be removed. That is to say, we can optimize the weak measurement by using only one GTP to implement the post-selection procedure. In practice, although the reflected field actually is not null because of its finite size, and the transformation from s-polarization to p-polarization has been demonstrated, the p-polarization component is still much smaller than the s-polarization component [32]. It is still effective to take the polarization selectivity of Brewster angle incidence as the preselection procedure in weak measurements. Therefore, it just needs to insert one nearly p-polarized GTP in the reflected beam to magnify the SDSs when the incident beam is reflected at Brewster angle. Figure 2 shows the schematic process, where $A _{\omega }$ is the amplifying factor. Based on this guideline, we configure our experimental scheme as follows.

Fig. 2

Weak measurement scheme with preselection and post-selection. $A _\omega$ denotes the amplifying factor

Figure 3 illustrates the experimental setup. The Ar$^{3+}$ laser generates a vertically polarized Gaussian beam at 514.5 nm with beam waist radius of 1 mm. The polarization orientation of the Gaussian beam is changed by passing through a half wave plate (HWP) and then is focused at the interface between the air and a standard right angle prism (K9, $n = 1.516$) by lens $L_1$. By rotating the HWP, it is convenient to change the polarization angle $\gamma _i$ of the incident beam. The prism is mounted on a precision rotation stage guaranteeing the exact Brewster incident angle. And then, the reflected beam orderly passes through the GTP and a collimated lens $L_2$. Eventually, a charge coupled device (CCD) is placed behind lens $L_2$ to measure the profile and centroid of the reflected beam. In this setup, the out-of-plane and in-plane SDSs occur at the hypotenuse plane of the prism, which can be inferred from the magnified shift obtained by numerical analysis of the recorded images. Note that, quite different from the setup in [3, 9] and [12], only one post-selection GTP is employed in our solution to simultaneously characterize the out-of-plane and in-plane SDSs. In our experiment, the polarization direction of the post-selection GTP has a tiny angle with respect to the $x _r$ direction, denoted as $\varepsilon$; thus, the weak value amplifying factor is $A _{\omega } = F /\varepsilon$, with $F = 4\pi y _{L2}^2/(\lambda f )$, where f is the focal length of lens $L_2$, and $y _{L2}^2$ is the variance of the y-direction transverse distribution of reflected beam profile after lens $L_2$ [3, 4].

Fig. 3

Experimental setup for characterizing the out-of-plane and in-plane SDSs of beam incident at $\theta _B$. Ar$^{3+}$ laser: 514.5 nm; $\lambda$/2: half wave plate; GTP: Glan–Taylor polarizer; $L_1$ and $L_2$: lenses with both 50-mm focal lengths; CCD: charge coupled device; insets: theoretical and experimental intensity distributions of p-polarized incident beam reflected at $\theta _B$

4 Experiment results and discussion

In our experiment, incidence with Brewster angle is a prerequisite. To achieve this condition, the polarization direction of incident beam is firstly set along $x _i$ axes. It is well known that none of the light energy is reflected for such a p-polarized beam incoming exactly at Brewster angle. However, for the p-polarized beam with bounded width, such as a Gaussian beam, which contains a series of plane wave components, only the components with $k _{ix}=0$ and $k _y=0$ (i.e., the central plane wave component) are exactly launched at $\theta _B$, and experience the extinction in the reflection field. The non-central plane wave components ($k _{ix}\ne 0$) still partially survive after reflection. Accordingly, the intensity pattern of the reflected beam presents vertically symmetric intensity profile, with a linear dip in the center region, similar to the $\hbox {TEM}_{10}$ mode [22]. In such a case, the numerically simulated intensity distribution of reflected field based on (4) is depicted in the insets in Fig. 3. This intuitive phenomenon can be used to determine the incident angle [22]: When the linear dip is adjusted to the center of the reflected beam pattern by rotating the prism, the central plane wave component of the input beam is exactly incident at $\theta _B$, and the incident angle for the input Gaussian beam with bounded width can also be considered as $\theta _B$. The experimentally measured intensity distribution of such a case is also shown in the inset in Fig. 3. Furthermore, although the input beam is p-polarized, a weak s-polarized component still appears in the reflection field due to cross polarization effect [32]. According to [33], the ratio of the s-component to the p-component for Brewster incidence is about $\rho =0.2$.

Fig. 4

Theoretical and experimentally measured intensity profiles of the reflected light after passing through $L_2$. The incident polarization angle is $\gamma _i =30^{\circ }$

From our theoretical prediction, the out-of-plane and in-plane SDSs are strongly dependent on the polarization angle $\gamma _i$. In the following, utilizing the developed weak measurement scheme, we determine the relationship between spatial SDSs and polarization angle $\gamma _i$ of a Gaussian beam incident at Brewster angle. Figure 4 depicts the theoretical and experimentally measured intensity profiles of the reflected beam after lens $L_2$ when $\gamma _i=30^{\circ }$. The left, middle, and right columns correspond to the cases of $\varepsilon =-1^{\circ }$, $0^{\circ }$, and $1^{\circ }$, respectively. The solid red point denotes the barycenter of the beam profile. Due to the destructive interference of the two splitting spin components, the reflected beam intensity behind GTP redistributes. As a result, the barycenter of the spots moves away from geometric center when $\varepsilon \ne$0. Comparing the barycenter of the beam with $\varepsilon =-1^{\circ }$ or $\varepsilon =1^{\circ }$ to $\varepsilon =0^{\circ }$, we can directly obtain the magnified in-plane SDS ($\Delta _x = A _{\omega }\delta _x$) and out-of-plane SDS ($\Delta _y = A _{\omega }\delta _x$). The metrical shifts are approximately enhanced $5.7\times 10^3$ times compared with original shifts, where $\varepsilon \approx 1.75 \times 10^{-2}$rad (approximately 1$^{\circ }$) and $F \approx 100$ for both in-plane and out-of-plane shifts. As a consequence, the magnified displacements can be confirmed accurately.

Fig. 5

a Out-of-plane SDS ($\delta _{y|+\rangle }$) and b in-plane SDS ($\delta _{x|+\rangle }$) of the $|+\rangle$ spin component versus the polarization angle $\gamma _i$ at Brewster angle. The curves and dots denote the theoretical and experiment results, respectively

The out-of-plane and in-plane shifts of the two spin components ($|+\rangle$ and $|-\rangle$) have the same magnitude but opposite sign. Figure 5 gives the close dependence of out-of-plane and in-plane shifts of $|+\rangle$ spin component on the polarization angle $\gamma _i$ at Brewster angle incidence, where the solid curves and dots correspond to the theoretical and experiment results, respectively. We measure the shifts every 10$^{\circ }$. It is clear that the out-of-plane SDS of $|+\rangle$ spin component along y-direction increases from 0 to 55.9 nm with $\gamma _i$ varying from 0$^{\circ }$ to 90$^{\circ }$; then, as $\gamma _i$ further varies from 90$^{\circ }$ to 180$^{\circ }$, the shift analogously decreases from 55.9 nm to 0. Similarly, the in-plane SDS of $|+\rangle$ spin component along $x _r$ direction increases from 0 to 55.9 nm with $\gamma _i$ varying from 0$^{\circ }$ to 57.36$^{\circ }$; then, the shift decreases to 0 with $\gamma _i$ varies from 57.36$^{\circ }$ to 90$^{\circ }$. Nevertheless, when $\gamma _i$ further varies from 90$^{\circ }$ to 180$^{\circ }$, the shift changes analogously, but along opposite direction. Those distinct change rules can be theoretically explained, that the in-plane SDS is mainly determined by factor sin(2$\gamma _r$) [according to (6)], which covers both negative and positive values. i.e., when $\gamma _i$ changes from 90$^{\circ }$ to 180$^{\circ }$, the in-plane SDS experiences the same variation rule but opposite direction. As a result, we can reverse the spin-dependent shift direction by changing the incident polarization angle $\gamma _i$, while, based on (7), the out-of-plane SDS is related to sin$\gamma _r^2$, which only obtains negative or positive value. Thus, the out-of-plane SDS direction keeps unchanged. In addition, the two kinds of shifts almost have the same maximum value.

5 Conclusion

In summary, we demonstrate experimentally the optimized weak measurement incorporated with polarization selectivity of Brewster angle incidence. This modified scheme is still effective when the Brewster angle incidence is warranted. In such a case, we measure the spatial spin-dependent shifts of a linearly polarized beam reflected upon the air–glass interface. The out-of-plane and in-plane SDSs almost have the same magnitude of maximum value albeit at different incident polarization angle. The experiment results show that it is convenient to reverse the in-plane SDS direction by adjusting the incident polarization angle and to control the out-of-plane and in-plane SDSs direction separately. This may possess potential applications in polarization modulator based on SHEL, which can be used to design nano-optical devices and realize precision metrology. In addition, this scheme may enrich the application of weak measurement.