1 Introduction

Laser systems can produce on-target intensities of the order of 1022 W/cm2 and peak powers beyond 1 PW [1–8]. At these power and intensity levels, the discrete prepulses and incoherent pedestal can induce target expansion or melting. The resulting target modification can have an effect on the interaction efficiency of the main pulse with the target [9–15]. Characterizing the contrast of the short optical pulses delivered by these systems has therefore become increasingly important. The incoherent fluorescence generated by laser or parametric amplifiers is a major source of contrast degradation. Reducing and characterizing the amount and temporal extent of the resulting incoherent pedestal is an active subject of investigation [16–19]. The temporal contrast of laser pulses is commonly measured with fast photodetection and nonlinear cross-correlators [9, 20–22]. Performing and interpreting high-dynamic-range temporal contrast measurements are difficult tasks. When the photodetection and nonlinear interactions are performed in the near field or are spatially averaged, the diagnostic typically measures the power contrast, i.e., the ratio of the peak power of the main pulse to the power of prepulse features such as discrete coherent pulses and incoherent pedestal, and there is no simple link between the measured power versus time and the intensity contrast. Because the local interaction of light with matter is intensity dependent, it is more relevant to determine the intensity contrast, i.e., the ratio of the main-pulse intensity to the prepulse intensity, for example, at the center of the focused beam. This is especially important when the prepulse features and the main pulse have different spatial coherence properties leading to nonidentical on-target focal spots. Such information is even more relevant for some particular interaction or target geometries, e.g., those associated with cone-in-shell implosions in the context of fast ignition [23]. One approach to determining the intensity contrast via optical means requires one to isolate a relevant (small) region of interest of the focused beam, then precisely characterize the temporally resolved power in that particular region. Although this is conceptually simple, this is not commonly done in practice. When the laser system properties are stable, another approach consists in characterizing the spatial and temporal properties of the fluorescence generated by each amplifier operated in unseeded conditions [19].

A formalism to predict the on-shot intensity contrast is presented and experimentally validated on the OMEGA EP Laser System [6]. Each OMEGA EP short-pulse beamline has an optical parametric chirped pulse amplification (OPCPA) front end that seeds large-scale Nd:glass amplifiers [6, 22]. The optical components following the front end, including the amplifiers, mirrors, and diffraction gratings, have aberrations that can only be partially corrected by deformable mirrors, in particular at high spatial frequencies. The front-end parametric amplifiers generate incoherent contrast-deteriorating fluorescence that has a significantly extended far field compared to the coherent amplified signal beam, which is typically close to the diffraction limit. In these conditions, the on-target incoherent and coherent focal spots can differ significantly, but we demonstrate that the incoherent focal spot and the relative intensity contrast can be determined from the on-shot coherent focal spot and power contrast. This approach is applicable to other laser systems where determining the incoherent focal spot is nontrivial, for example, when the overall laser system is far from the diffraction limit and the incoherent fraction of the pulse has spatial properties different from the coherent pulse. Expressions for the incoherent focal spot and the intensity-contrast based on coherence theory are derived in Sect. 2. Section 3 presents validation experiments and the on-shot intensity-contrast measurement on a short high-energy pulse.

2 Determination of the incoherent focal spot and intensity contrast

2.1 Incoherent focal-spot determination

A high-energy laser system is a complex optical system that includes amplifiers, image relays, stretching and compression elements, and a focusing element. For this work, the system is divided into two sections: a high-gain front end in which the incoherent pedestal is generated and a low-gain main section (Fig. 1). We restrict our analysis to the situation where the spatial properties of the incoherent and coherent fraction of the pulse are significantly different and the main laser section is highly aberrated. When the main section is not highly aberrated, it is straightforward to link the spatial properties of the incoherent pedestal after the front end and in the target plane. When the temporally incoherent fluorescence and the temporally coherent main pulse have similar spatial properties, e.g., when they originate from an amplifier having a single spatial mode [19], their spatial properties in the target plane are not expected to be significantly different.

Fig. 1
figure 1

System description and definitions. Linear propagation between an input focal plane after the high-gain front end generating the incoherent pedestal and an output focal plane is considered

Full size image

The on-shot incoherent focal spot is calculated using the on-shot coherent focal spot and spatial properties of the incoherent pedestal measured in the front end. Linear optical propagation is described using mutual-intensity functions to provide a general formalism that can be applied to coherent and incoherent sources [24]. The propagation between an input focal plane, chosen between the front end and main laser section, and an output focal plane, where the target is located, is described with an amplitude spread function. This assumes that the state of the system is identical for the coherent and incoherent fraction of the pulse, in particular, that the propagation is linear for the high-energy coherent pulse. The derivation remains valid as long as nonlinear effects such as self-phase modulation do not significantly modify the propagation. Safe operation of these systems precludes intensity levels that significantly modulate the spatial phase of the beam and induce self-focusing. The derivation assumes that a one-to-one imaging condition exists between these two planes because magnification, rotation, and symmetries are easily taken into account numerically.

Laser systems contain polarization-dependent components (e.g., polarizers, diffraction gratings) and processes (e.g., laser amplification, parametric amplification) that constrain the field to a well-defined polarization state represented by a scalar quantity. These systems are in general optimized to minimize the spatial variations of spectral/temporal properties of the optical pulse that lead to detrimental spatiotemporal coupling and decrease the achievable peak power. In the absence of spatiotemporal coupling, the electric field and intensity are separable functions of the spatial and temporal coordinates. In this subsection, we focus on determining the spatial distribution of the focal spot in the output plane, i.e., a quantity proportional to the fluence (time-integrated intensity); therefore, no attempt is made to derive absolute physical values of the field, fluence, or intensity. The field distributions in the input and output planes are represented by scalar quantities \(E_{\text{in}} \left( {\vec{r}} \right)\) and \(E_{\text{out}} \left( {\vec{R}} \right)\) without explicitly stating the temporal dependence. Following the definitions of Ref. [24], the mutual intensity functions in the input and output planes are given by

$$J_{\text{in}} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right) = E_{\text{in}} \left( {\vec{r}_{1} } \right)E_{\text{in}}^{ *} \left( {\vec{r}_{2} } \right)$$
(1)

and

$$J_{\text{out}} \left( {\vec{R}_{1} ,\vec{R}_{2} } \right) = E_{\text{out}} \left( {\vec{R}_{1} } \right)E_{\text{out}}^{ * } \left( {\vec{R}_{2} } \right).$$
(2)

The field fluences in these two planes are

$$F_{\text{in}} \left( {\vec{r}} \right) = E_{\text{in}} \left( {\vec{r}} \right)E_{\text{in}}^{*} \left( {\vec{r}} \right) = J_{\text{in}} \left( {\vec{r},\vec{r}} \right)$$
(3)

and

$$F_{\text{out}} \left( {\vec{R}} \right) = E_{\text{out}} \left( {\vec{R}} \right)E_{\text{out}}^{ *} \left( {\vec{R}} \right) = J_{\text{out}} \left( {\vec{R},\vec{R}} \right).$$
(4)

The amplitude spread function \(K\left( {\vec{R},\vec{r}} \right)\) is by definition the output field amplitude at coordinates \(\vec{R}\) resulting from a δ-function input field amplitude at coordinates \(\vec{r}.\) It links the input and output mutual-intensity functions via a superposition integral consisting of a double integration in the input space (i.e., four single-dimensional variables):

$$J_{\text{out}} \left( {\vec{R}_{1} ,\vec{R}_{2} } \right) = \iint {{\text{d}}\vec{r}_{1} {\text{d}}\vec{r}_{2} J_{\text{in}} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right)K\left( {\vec{R}_{1} ,\vec{r}_{1} } \right)K^{*} \left( {\vec{R}_{2} ,\vec{r}_{2} } \right)}.$$
(5)

For target interaction experiments, the interest lies in the spatial distribution of the output intensity given by

$$F_{\text{out}} \left( {\vec{R}} \right) = \iint {{\text{d}}\vec{r}_{1} }{\text{d}}\vec{r}_{2} J_{\text{in}} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right)K\left( {\vec{R},\vec{r}_{1} } \right)K^{ * } \left( {\vec{R},\vec{r}_{2} } \right).$$
(6)

For a coherent diffraction-limited field located at \(\vec{r} = \vec{0},\) the input correlation function can be approximated in Eq. (6) by \(J_{\text{in}} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right) = F_{\text{in}}^{\text{coh}} \delta \left( {\vec{r}_{1} } \right)\delta \left( {\vec{r}_{2} } \right)\) and the output fluence is

$$F_{\text{out}}^{\text{coh}} \left( {\vec{R}} \right) = F_{\text{in}}^{\text{coh}} \left| {K\left( {\vec{R},\vec{0}} \right)} \right|^{2} .$$
(7)

For a spatially incoherent field distribution, there is no correlation between two distinct spatial points, and the mutual intensity in the input plane is \(J_{\text{in}} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right) = F_{\text{in}}^{\text{inc}} \left( {\vec{r}_{1} } \right)\delta \left( {\vec{r}_{1} - \vec{r}_{2} } \right).\) This simplifies Eq. (6) to

$$F_{\text{out}}^{\text{inc}} \left( {\vec{R}} \right) = \int {{\text{d}}\vec{r}F_{\text{in}}^{\text{inc}} \left( {\vec{r}} \right)\left| {K\left( {\vec{R},\vec{r}} \right)} \right|^{2} .}$$
(8)

If \(\left| {K\left( {\vec{R},\vec{r}} \right)} \right|^{2}\) is known for all \(\vec{r}\) and \(\vec{R},\) the output incoherent fluence distribution can be determined by a superposition integral of that function with the input incoherent fluence distribution [Eq. (8)]. This is practically difficult to achieve because the point-spread function in the output plane must be measured for a Dirac input field distribution at every input point. The condition \(\left| {K\left( {\vec{R},\vec{r}} \right)} \right|^{2} = \left| {K\left( {\vec{R} - \vec{r},\vec{0}} \right)} \right|^{2}\) is fulfilled for an isoplanatic (space-invariant) system. This is generally the case for a laser system in which the tightest far-field pinholes are in the front end and far-field pinholes in the main laser section do not restrict the propagation of the main laser pulse. This relation simplifies Eq. (8) into a convolution that can be combined with Eq. (7) to give

$$F_{\text{out}}^{\text{inc}} \left( {\vec{R}} \right) \propto \int {{\text{d}}\vec{r}F_{\text{in}}^{\text{inc}} } \left( {\vec{r}} \right)F_{\text{out}}^{\text{coh}} \left( {\vec{R} - \vec{r}} \right).$$
(9)

Equation (9) shows that the output fluence distribution for an incoherent source propagating through the laser system, \(F_{\text{out}}^{\text{inc}} ,\) is proportional to the convolution of the output fluence distribution of a coherent Dirac input field \(F_{\text{out}}^{\text{coh}}\) with the input incoherent fluence distribution \(F_{\text{in}}^{\text{inc}} .\) This relation is consistent with the fact that an incoherent imaging system is linear in fluence and has the coherent point spread function for impulse response [24]. The focal spot of the incoherent fraction of the pulse cannot be directly measured on-shot because the coherent fraction of the pulse typically has much more energy than its incoherent counterpart, but Eq. (9) allows for its indirect determination using directly measured quantities. Equation (9) is primarily useful when the main laser section is aberrated and the coherent focal spot is much smaller than the incoherent focal spot after the front end. For a non-aberrated system, the incoherent focal spot has the same shape in the input and output plane.

The on-shot focal spot of the main laser pulse can be determined either directly or via near-field intensity and wavefront measurements [25], yielding \(F_{\text{out}}^{\text{coh}}\) up to a proportionality constant. An on-shot measurement with high-energy amplification in seeded conditions is crucial to ensure the accuracy and relevance of the determined incoherent focal spot if the coherent focal spot is fluctuating from shot to shot because of wavefront distortions. The incoherent contribution to the main amplified pulse is dominated by the high-gain front end. For a parametric or laser amplifier operated close to saturation, the amount of generated fluorescence can be much larger in unseeded conditions than in seeded conditions [16–18]. Because Eq. (9) only describes the shape, but not the physical value, of the far-field fluence distribution, the incoherent focal spot directly measured in unseeded conditions is used as \(F_{\text{in}}^{\text{inc}}\) in Eq. (9). This measurement is relevant as long as the spatial far-field fluence distributions are similar in seeded and unseeded conditions up to a proportionality constant. An uncertainty is introduced when that is not the case, but the effect is assumed to be small considering that far-field distributions are typically set by system geometry, e.g., pinhole size, or nonlinear interaction geometry, e.g., phase matching.

Fluorescence, either from stimulated emission or a parametric nonlinear interaction, is composed of amplified noise photons. When the signal is amplified in the far field, i.e., in a plane that is reimaged to the target plane, the relation \(J_{\text{in}}^{\text{inc}} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right) = F_{\text{in}}^{\text{inc}} \left( {\vec{r}_{1} } \right)\delta \left( {\vec{r}_{1} - \vec{r}_{2} } \right)\) indicates that there is no spatial coherence between two distinct far-field points. When the amplifiers operate in the signal near field, the front-end fluorescence is expected to be spatially uncorrelated in that plane. This can be expressed in terms of mutual intensity by \(J_{\text{in,nf}}^{\text{inc}} \left( {\vec{\rho }_{1} ,\vec{\rho }_{2} } \right) \propto F_{\text{in,nf}}^{\text{inc}} \left( {\vec{\rho }_{1} } \right)\delta \left( {\vec{\rho }_{1} - \vec{\rho }_{2} } \right),\) where the subscript nf and the variables \(\vec{\rho }_{1}\) and \(\vec{\rho }_{2}\) relate to the near field and \(F_{\text{in,nf}}^{\text{inc}} \left( {\vec{\rho }_{1} } \right)\) is the fluorescence beam profile. The mutual intensities calculated in two planes related by a Fourier transform, e.g., in the near field and far field of the beam, are a Fourier transform pair (see “Focal-Plane to Focal-Plane Coherence Relationships” in Ref. [24], p. 292). For an incoherent near field, this leads to the expression \(J_{\text{in}}^{\text{inc}} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right) = \int {F_{\text{in,nf}}^{\text{inc}} \left( {\vec{\rho }_{1} } \right)\exp \left[ {i\vec{\rho }_{1} \cdot \left( {\vec{r}_{1} - \vec{r}_{2} } \right)} \right]d\vec{\rho }_{1} }\). When the incoherent and coherent near-field beam profiles are similar, that expression shows that correlations between two far-field points at coordinates \(\vec{r}_{1}\) and \(\vec{r}_{2}\) are only expected for points separated by a distance smaller than the coherent focal-spot size. In the framework of this derivation, where the main laser section has significant aberrations leading to an amplitude spread function K much larger than the diffraction-limited focal-spot size, the far-field mutual intensity function \(J_{\text{in}}^{\text{inc}} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right)\) can be simplified to \(F_{\text{in}}^{\text{inc}} (\vec{r}_{1} )\delta \left( {\vec{r}_{1} - \vec{r}_{2} } \right)\) to derive Eq. (8) from Eq. (6).

2.2 Intensity-contrast determination

Equation (9) determines the shape of the incoherent focal spot, but absolute or relative intensity information cannot be determined without some knowledge of the temporal features of the coherent pulse and incoherent pedestal. The main-pulse intensity is obtained using the on-shot focal spot, on-shot energy, and on-shot pulse duration (or, more generally, the pulse shape). The on-shot incoherent intensity can be predicted with a similar set of data, where the on-shot focal spot is obtained from Eq. (9) and knowledge of the incoherent energy and instantaneous power versus time provided by a temporal power-contrast diagnostic. In the absence of spatiotemporal coupling in the coherent and incoherent field distributions, the output physical intensities are written as

$$I^{\text{coh}} \left( {\vec{R},t} \right) = I_{\text{peak}}^{\text{coh}} \cdot F_{\text{out}}^{\text{coh}} \left( {\vec{R}} \right) \cdot P^{\text{coh}} \left( t \right),$$
(10)
$$I^{\text{inc}} \left( {\vec{R},t} \right) = I_{\text{peak}}^{\text{inc}} \cdot F_{\text{out}}^{\text{inc}} \left( {\vec{R}} \right) \cdot P^{\text{inc}} \left( t \right),$$
(11)

where \(I^{\text{coh}}\), \(I^{\text{inc}}\), \(I_{\text{peak}}^{\text{coh}} \;\), and \(I_{\text{peak}}^{\text{inc}} \;\) are in units of W/cm2, and F and P are dimensionless representations of the fluence and instantaneous power distributions peak-normalized to 1. A temporal contrast diagnostic integrating over the entire beam yields signals proportional to

$$S^{\text{coh}} \left( t \right) = I_{\text{peak}}^{\text{coh}} \cdot P^{\text{coh}} \left( t \right) \cdot \int {{\text{d}}\vec{R}F_{\text{out}}^{\text{coh}} \left( {\vec{R}} \right)}$$
(12)

and

$$S^{\text{inc}} \left( t \right) = I_{\text{peak}}^{\text{inc}} \cdot P^{\text{inc}} \left( t \right) \cdot \int {{\text{d}}\vec{R}F_{\text{out}}^{\text{inc}} \left( {\vec{R}} \right)} .$$
(13)

A nonlinear scanning cross-correlator generally measures an experimental trace that contains the two signals described by Eqs. (12) and (13). When using a photodiode to measure the on-shot power contrast, only the signal of Eq. (13) is measured on-shot and the signal of Eq. (12) heavily saturates the photodetection system. The latter is typically determined from precalibration of the diagnostic or via another photodetection system operating with less energy. The on-shot intensity contrast \(I_{\text{peak}}^{\text{coh}} /I_{\text{peak}}^{\text{inc}}\) is determined using the signals of Eqs. (12) and (13) and the integrals \(\int {{\text{d}}\vec{R}F_{\text{out}}^{\text{coh}} \left( {\vec{R}} \right)}\) and \(\int {{\text{d}}\vec{R}F_{\text{out}}^{\text{inc}} \left( {\vec{R}} \right)}\) calculated, respectively, with the measured coherent output focal spot and determined incoherent output focal spot [Eq. (9)]. The intensity contrast is the product of the measured spatially integrated power contrast and the ratio of these two integrals. When the incoherent focal spot has much larger spatial extent than the coherent focal spot, one has \(\int {{\text{d}}\vec{R}F_{\text{out}}^{\text{inc}} \left( {\vec{R}} \right)} \gg \int {{\text{d}}\vec{R}F_{\text{out}}^{\text{coh}} \left( {\vec{R}} \right)}\), i.e., the relative intensity contrast is much higher than the relative power contrast.

3 Experimental results

Equation (9) was experimentally verified on the OMEGA EP laser [6, 22]. For short-pulse operation, the 5-Hz OPCPA front end produces 100-mJ pulses in an apodized beam that seeds a series of large-scale Nd:glass amplifiers. The front-end gain is typically 108. The gain in the subsequent amplification stages is of the order of 104. The input focal plane is chosen between the high-gain OPCPA stages and the main beamline that introduces most of the spatial aberrations. The amplified beam is re-imaged multiple times throughout the laser system by propagation in transport spatial filters that incorporate a far-field pinhole. The front end contains the tightest pinholes (properly scaled in terms of f number); therefore, beamline pinholes do not break the isoplanarity assumption between the input and output far-field planes.

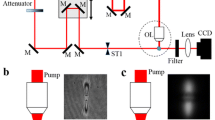
For experimental validation of Eq. (9), the incoherent input focal spot \(F_{\text{in}}^{\text{inc}}\) is measured with a camera located at the focal plane of a lens when the OPCPA seed is blocked (Fig. 2a). The OPCPA system is based on two stages of lithium triborate (LBO) pumped at 526.5 nm in a slightly noncollinear configuration for amplification around 1053 nm. Therefore, the incoherent input far field is a fraction of a parametric fluorescence arc centered at the OPCPA pump far field after clipping by various pinholes. The output far fields were directly measured using a focal-spot microscope at the focus of the off-axis parabola focusing the OMEGA EP pulse in the OMEGA target chamber [25]. This was performed with the seeded OPCPA to determine the coherent far field \(F_{\text{out}}^{\text{coh}}\) for application in Eq. (9) and with the unseeded OPCPA for comparison to the focal spot \(F_{\text{out}}^{\text{inc}}\) determined using Eq. (9). These measurements were made within a few minutes of each other for a given correction state of deformable mirrors in the laser system because of practical operational limitations.

Fig. 2
figure 2

Data measured for output incoherent focal-spot calculation: a input incoherent far field; b output coherent far field

Full size image

The coherent output far field is shown in Fig. 2b. The incoherent output far field calculated using the data plotted in Fig. 2 and Eq. (9) is plotted in Fig. 3 alongside the directly measured far field. All far fields are scaled to the output-plane far-field axes to facilitate comparison. The good agreement between measurement and calculation is confirmed in Fig. 4, where the lineouts of the calculated incoherent focal spot along x and y are compared to the lineouts of 20 consecutive incoherent focal-spot acquisitions.

Fig. 3
figure 3

Measured and calculated output incoherent far fields on a linear scale and log scale

Full size image
Fig. 4
figure 4

Lineouts of calculated incoherent focal spot (circles) and of 20 consecutively measured incoherent focal spots (continuous lines) in a x and b y direction

Full size image

The full width at half maximum (FWHM) along x and y of the predicted lineouts are 27.1 and 43.7 μm, respectively, while the FWHM’s of the lineouts of the measured focal spots are 36.1 and 43.2 μm, respectively, with a standard deviation of 2.3 and 1.2 μm, respectively. This agreement is satisfactory considering that there are multiple factors that could influence the accuracy of this experimental validation. First, the coherent and incoherent focal spots cannot be measured simultaneously. The coherent focal spot was measured after optimization of the large-scale OMEGA EP deformable mirror for best focus, after which the focal-spot measurement configuration was modified to measure the incoherent focal spot in the target chamber. Shot-to-shot variations of the coherent focal spot are observed even with the deformable mirror at an optimal setting because of turbulence, and deterioration of the coherent focal spot quality is typically observed over the few minutes that were required to switch the measurement system between the coherent and incoherent measurements. The x direction corresponds to the diffraction direction for the grating compressor. A small amount of residual angular dispersion (e.g., because of slight compressor misalignment) would lead to more elongation of the focal spot in that direction for the broadband parametric fluorescence than for the 8-nm-bandwidth OPCPA pulse. These effects impact the experimental validation but have no practical consequences on the ability to determine the on-shot incoherent focal spot because this determination is based on the on-shot coherent focal spot and the parametric fluorescence experiences the same gain narrowing as the signal.

The intensity prepulse contrast on a 1-kJ, 10-ps OMEGA EP shot has been determined. The on-shot focal spot of the main pulse is predicted using the measured on-shot near field and wavefront [25]. The temporally resolved power contrast of the pulse is obtained using a set of calibrated photodiodes [22] and the incoherent pedestal is maximal approximately 1.2 ns before the main pulse, where it is 66 dB down from the main pulse (Fig. 5a). The coherent focal spot is shown in Fig. 5b, where a single high-intensity peak culminating at \(I_{\text{peak}}^{\text{coh}} =\) 5.9 × 1019 W/cm2 is visible. High-frequency wavefront modulations that are not compensated by the deformable mirror lead to far-field features at a distance up to 20 μm from the main peak. The determined incoherent focal spot is clearly much broader than the coherent focal spot; it has a peak intensity equal to \(I_{\text{peak}}^{\text{inc}} =\) 1.6 × 1012 W/cm2 (Fig. 5c). The intensity contrast is 76 dB—a decade better than the power contrast—because of the poorer focusability of the incoherent pedestal (Fig. 5d).

Fig. 5
figure 5

a Measured instantaneous power of the incoherent pedestal of an OMEGA EP 1-kJ, 10-ps shot scaled to the peak power of the pulse; b intensity distribution determined at the peak of the pulse; c intensity distribution determined at the peak of the incoherent pedestal (~1.2 ns before the main pulse) on the same shot. d Determined relative intensity contrast at the point in the beam where the peak intensity is the highest

Full size image

4 Conclusions

In conclusion, a formalism has been developed to describe the propagation of the incoherent fraction of an optical pulse in a laser system. The incoherent focal spot in the target plane is predicted from the coherent focal spot in that plane and the incoherent far-field distribution in the front end. The resulting on-shot prediction of the incoherent focal-spot shape and intensity contrast using quantities that are commonly and directly measured is particularly useful when the laser system is aberrated. An experimental validation on the OMEGA EP Laser System using the front-end parametric amplifiers showed that the calculated incoherent focal spot agrees well with the focal spot directly measured at the center of the target chamber. An on-shot determination of the intensity contrast on a 1-kJ, 10-ps OMEGA EP pulse showed that the intensity contrast is ~10× higher than the power contrast, demonstrating the importance of characterizing the intensity contrast to significantly improve the understanding of experimental laser–matter intensity-dependent interactions.