1 Introduction

The study of high-order nonlinearities (HON) in transparent media has been attracting large interest because of its association with beam self-focusing, spectral broadening, spatial soliton excitation, and filamentation, among other nonlinear (NL) phenomena [1–3]. It is currently known that for peak powers below but near the critical power for self-focusing, the NL response is dominated by saturation of the Kerr effect and free-carriers generation, sometimes referred to as plasma formation by analogy with the case of gases [4, 5]. The balance between self-focusing and saturation or defocusing due to free-carriers leads to filamentation in gases which is a process that maintains a narrow beam diameter and high peak intensity all along the light beam propagation.

Recently, it was discussed that the saturation of Kerr effect associated with multiphoton absorption (MPA) plays an important role below the onset of filamentation and laser-induced damage in solids [6]. More recently, it was demonstrated that saturation of the Kerr effect, associated with NL absorption, could explain filamentation in liquid CS2 [7]. It was also shown that the usual way to describe the NL dynamics of a light beam in CS2 using the NL Schrödinger equation (NLSE), possibly modified by high-order terms, is not sufficient to describe experiments made at very high intensities near the onset of filamentation. Accurate measurements of the effective NL refractive index, n 2eff, have shown a specific behavior which describes filamentation [7] and self-trapping of vortex beams [8] in CS2 showing good agreement between theory and experimental observations.

However, with respect to toluene (C7H8), another important organic solvent studied since the early days of NL optics, nothing was reported concerning its HON neither filamentation.

In the present paper, we report on NL experiments in toluene and show that two regimes exist, one where HON play a key role, and the other which is dominated by free-carriers generation. Measurements of the NL refractive index as well as the NL absorption allow to determine, in the first regime, values of the higher-order NL indexes, and in the second regime values of the multiphoton ionization coefficient, for both wavelengths at 532 and 1064 nm in the ps range. As in the case of CS2 [7], we show that the usual description of n 2eff increasing linearly with the intensity is valid up to 2 × 1014 W/m2 in the green and up to 9 × 1014 W/m2 for the infrared (IR). For intensities larger than these values the solvent shows saturation that may be attributed to free-carriers generation, which is evidenced by the arising of high-order NL absorption and by changes in the slope of the transmitted beam phase-shift versus the incident intensity. As in Ref. [9] to explain the experimental observations, the mechanism proposed involves multiphoton ionization of the toluene molecules as a consequence of the self-focusing of the laser beam inside the cell.

2 Experimental details

Liquid toluene (C7H8) was obtained from Merck (purity >99.9) and contained in 2-mm-thick quartz cell for the experiments. The measurements were made using a Nd:YAG laser emitting at 1064 nm with 17-ps pulse duration (FWHM) at a repetition rate of 1 Hz and its second harmonic at 532 nm (12 ps, FWHM). The D4σ method [10, 11] was applied to characterize the intensity-dependent refractive index, and the usual open-aperture 4f-Z-scan technique [12] was used to determine the NL absorption coefficients. All measurements were performed with linearly polarized light.

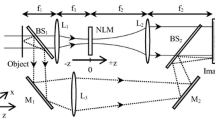
The setup used to implement the Z-scan D4σ measurements is similar to the one presented in [13] (see Fig. 1). The sample was mounted on a translation stage and moved along the beam direction (z axis) in the focus region. For each step of the motor (1 mm), a shutter was open to acquire an image of the pulse transmitted by the sample that was recorded by a CCD camera. The response behavior of the CCD sensor to optical power was checked to be linear. A second arm was used to monitor the energy fluctuation of the incident laser pulses (via lens L3). The 4f imaging system composed of two 20-cm focusing lenses is described with basis on Fourier optics [14]. The induced NL phase-shift and/or absorption originate changes in the transmitted beam in the image plane while moving the sample in the focal region, and this allows determination of the related NL parameters. The optical imaging system is aligned carefully to obtain a magnification equal to 1 such that it is possible to characterize accurately the profile of the beam at the entry in the linear regime which is a very important information. By using the optical transfer function related to the free-space propagation over a finite distance and considering the phase transformations due to the lenses composing the 4f-system, we simulate the propagation of the beam from the object to the image plane taking into account the transmittance of the NL medium positioned at each motor step used for the Z-scan measurement [14]. The transmittance of the NL medium is considered according to the evolution equations for the NL phase-shift and intensity in the thin sample approximation (see Eqs. (1), (3) below). Fits of the Z-scan profiles provide the NL refraction index and NL absorption coefficient of the medium by comparing numerical and experimental data. For each measurement, two sets of acquisitions were performed. The first set is in the NL regime and the second one in the linear regime, obtained by reducing the incident laser intensity; this was necessary to remove from the NL measurement results the diffraction, diffusion, and/or imperfection contributions due to sample inhomogeneity. Moreover, an image of the entry plane of the 4f-system allows the characterization of the circular aperture object that will be considered in the computer simulation; at 532 nm we measured a radius equal to 1.4 mm, and at 1064 nm the radius was 1.9 mm. As shown in [10] this procedure allows high-accuracy measurements even for relatively high absorption and large phase-shift when the signal is no more linear with the signal determined by the beam waist relative variation (BWRV) at the output measured by the CCD. The main source of uncertainty comes from the absolute measurement of the laser pulse energy because the accuracy of the joulemeter is about 10 %. In summary, the classical closed-aperture Z-scan method is based on the measurements of the Gaussian beam waist that passes through a circular aperture placed in the far-field region. The method is sensitive to point-beam stability because of the hard aperture. In the D4σ method we use a top-hat beam in a 4f imaging system and we acquire, on the CCD, the intensity profile I(x, y) after the interaction of the light with the NL material. The acquisitions obtained at z allow to compute the first- and the second-order moments of I(x, y). The method gives four times the standard deviation of the spatially limited intensity distribution. The reading of the image through a CCD allows to correct for point-beam instability following the centroid of the image position (first-order moment). The simulation of the whole process of image formation gives the NL parameters even in the presence of high NL absorption. No simplified formulas are used. More details on the D4σ method are given in Refs. [10, 13].

Fig. 1
figure 1

The 4f imaging system. The sample is scanned along the beam direction around the focal plane (Z = 0). The labels refer to: lenses (L1, L2, and L3), beam splitters (BS1 and BS2), CCD camera (CCD), and mirrors (M1 and M2)

Full size image

To take into account the contributions of the cells’ walls and the toluene inside the cell, one can consider the total NL phase-shift \( \Delta \varphi_{\text{tot}} = \Delta \varphi_{c} + \Delta \varphi_{t} \), that leads to the effective NL refractive index of toluene alone: \( n_{{2{\text{eff}}}} = {{\left[ {\left( {{{\lambda \Delta \varphi_{\text{tot}} } \mathord{\left/ {\vphantom {{\lambda \Delta \varphi_{\text{tot}} } {2\pi I_{0} }}} \right. \kern-0pt} {2\pi I_{0} }}} \right) - n_{2c} L_{c} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {{{\lambda \Delta \varphi_{\text{tot}} } \mathord{\left/ {\vphantom {{\lambda \Delta \varphi_{\text{tot}} } {2\pi I_{0} }}} \right. \kern-0pt} {2\pi I_{0} }}} \right) - n_{2c} L_{c} } \right]} L}} \right. \kern-0pt} L}_{t} \), where the subscript c stands for cell and t for toluene. The contribution of the walls is important when the liquid nonlinearity is comparable to the silica nonlinearity, as in water [13]. However, in the present case we observed that the induced NL phase-shift in the silica walls can be neglected when compared to the one induced in toluene that presents a NL refraction coefficient one order of magnitude larger. Therefore, we considered \( \Delta \varphi_{\text{tot}} \approx \Delta \varphi_{t} \).

3 Results and discussion

3.1 Nonlinear polarization versus multiphoton regimes

At relatively high intensity different phenomena may contribute to induce the losses which are observed at the output of the NL material. For experimental tractability, we assume that, under the slowly varying envelope and thin sample approximations, the evolution of the optical intensity, I, as a function of z′, the longitudinal-propagation axis inside the material, obeys a differential equation of the form:

$$ \frac{{{\text{d}}{\rm I}}}{{{\text{d}}z^{\prime } }} = - C_{N} I^{N}, $$
(1)

where N is an integer to be determined. Equation (1) is identical to the evolution equation for the intensity when the losses are due to N-photon absorption (NPA). However, in the present case, NPA is not the only mechanism present, but we use Eq. (1) to give a global macroscopic and phenomenological account of all losses. On the other hand, when free-electrons generation occurs, C N is nothing but the coefficient for multiphoton ionization, sometimes denoted by βK (with K = N). Taking into account the boundary conditions [\( I\left( {z^{'} = 0} \right) = I_{0} \left( {z,u,v,t} \right) \); \( I\left( {z^{'} = L} \right) = I_{L} \left( {z,u,v,t} \right) \)], with L denoting the thickness of the sample, the solution writes:

$$ I_{L} \left( {z,u,v,t} \right) = \frac{{I_{0} \left( {z,u,v,t} \right)}}{{\left[ {1 + \left( {N - 1} \right)C_{N} LI_{0} \left( {z,u,v,t} \right)^{N - 1} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {N - 1}}} \right. \kern-0pt} {N - 1}}}} }}, $$
(2)

where z represents the position of the sample in the focus region, u = x/λf and v = y/λf are the normalized spatial frequencies, and \( I(z,u,v,t) \) denotes the intensity of the laser beam inside the sample. For the open-aperture Z-scan profile (see Fig. 2), Eq. 2 is integrated numerically over space and time (over u, v, and t) using a Gaussian temporal profile and the real spatial profile of the beam at the entry (after propagation to the z position in the focal region). Indeed, the total energy at the output of the sample can be obtained without having to include the rest of propagation up to the image plane. The numerical integration at this level for each z position using Eq. 2 is advantageous because it avoids the approximations involved by the approach which takes analytically into account the relatively low NL absorption correction in the far-field (i.e., \( \left| {\left( {N - 1} \right)C_{N} LI_{0} \left( {z,u,v,t} \right)^{N - 1} } \right| \le 1 \)). Thus, once the open-aperture Z-scan is performed the effective losses coefficient C N can be deduced, for any regime by fitting the normalized transmittance data profile.

Fig. 2
figure 2

(Color online): Dependence of C3 (m3/W2), the measured effective 3PA coefficient in toluene at 532 nm (green circle) and 1064 nm (red stars) as a function of the intensity. The inset is a zoom showing C 3 versus I 0 (in the IR) for an y-axis scale 20 times smaller

Full size image

To illustrate our numerical procedure, Fig. 2 shows the evolution of this coefficient as a function of the incident intensity (the choice of N = 3 is discussed in sect. 3.3 below and does not mean that the measured NL losses are due to three-photon absorption). A steep discontinuity for the green wavelength data at about 3 × 1014 W/m2 can be noticed. We attribute this behavior to the molecule multiphoton ionization intensity threshold. A smoother variation and lower values characterize the losses in the IR. As shown in the inset, a small increase of C 3 is observed at intensities higher than 1.3 × 1015 W/m2 remaining at a mean value about 20 times lower than that obtained in the green. The origin of the difference between the results obtained at both wavelengths is related to the ratio between band gap energy and incident photon energy, in relation with Keldysh theory [15].

For intensities smaller than 3 × 1014 W/m2 for the green and 13 × 1014 W/m2 for the IR, no absorption was detected which indicates that in this range of intensities no free-carriers are generated, and the electronic nonlinearities corresponding to the NL polarization of molecules, as described by the usual formalism of NL susceptibilities, are responsible for the observed Kerr effect and its saturation. For intensities larger than the values mentioned above, it is believed that NL absorption mainly results from photoionization and plasma formation.

3.2 NL refraction and n4 measurements

Our classical measurement procedure is built to consider the response of the material described by an effective cubic nonlinearity defined by C 2 (m/W), the second-order NL absorption coefficient, and \( n_{{2{\text{eff}}}} \left( {{\text{m}}^{2} /{\text{W}}} \right) \), the effective NL refractive index. In these conditions, the transmittance of the sample is described by \( T\left( {z,u,v} \right) = \left[ {1 + q\left( {z,u,v} \right)} \right]^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} \exp \left[ {j\Delta \varphi_{{_{\text{NL}} }}^{\text{eff}} \left( {z,u,v} \right)} \right] \), where \( q\left( {z,u,v} \right) = C_{2} LI\left( {z,u,v} \right) \). The NL phase-shift is represented by \( \Delta \varphi_{\text{NL}}^{\text{eff}} \left( {z,u,v} \right) = {{2\pi n_{{2{\text{eff}}}} LI_{{{\text{ef}}f}} \left( {z,u,v} \right)} \mathord{\left/ {\vphantom {{2\pi n_{{2{\text{eff}}}} LI_{{{\text{ef}}f}} \left( {z,u,v} \right)} \lambda }} \right. \kern-0pt} \lambda } \), where we define the effective intensity as \( I_{\text{eff}} \left( {z,u,v} \right) = I\left( {z,u,v} \right){{\log \left[ {1 + q\left( {z,u,v} \right)} \right]} \mathord{\left/ {\vphantom {{\log \left[ {1 + q\left( {z,u,v} \right)} \right]} {q\left( {z,u,v} \right)}}} \right. \kern-0pt} {q\left( {z,u,v} \right)}} \). The peak on-axis NL phase-shift at the focus is \( \phi_{{0{\text{eff}}}} = \Delta \varphi_{{_{\text{NL}} }}^{\text{eff}} (0,0,0) \). The latter can be deduced from the signal of the BWRV (for more details, see [10]). To obtain n 2eff, it is necessary to take into account the real absorption encountered by the material measured at this level considering C 2.

Figure 3 shows the effective phase-shift measured by using the BWRV method as a function of the incident intensity for both wavelengths. Notice the change of the slopes, which coincides exactly with the points where the NL absorption appears, at an intensity higher than 3 × 1014 W/m2 in the green and ~1.4 × 1015 W/m2 in the IR. Moreover, Fig. 4 demonstrates that at the same intensity levels n 2eff changes its behavior showing saturation in the green with noisy fluctuation and decreasing in the IR after reaching a maximum value. The results can be analyzed considering that generally the NL response of a material excited by high laser intensities could be due to self-focusing, NL absorption, and multiphoton ionization. Other contributions may be due to loss mechanisms, such as scattering, diffraction, and reflection due to the local presence of plasma, as well as thermal heating induced by the linear plasma absorption (free-electrons absorption). In principle, these mechanisms compete and the one which dominates depends on the laser intensity, the pulse width, band gap of the material, and the laser wavelength [16]. According to [16] for high laser intensities, the amount of ionized molecules would be relatively large; we refer to them as a “plasma” according to the common use; however, the density of free-carriers remains smaller than the density of neutral molecules (as we will see hereafter), and that no phase transitions is involved. The free-carriers would then contribute to the losses due to linear mechanisms, such as scattering, diffraction, and reflection due to the local presence of plasma, as well as thermal heating induced by the linear plasma absorption (free-electrons absorption). The plasma also contributes to the NL index n 2eff. Here, the contribution of the plasma negative nonlinearity is more important and the slope of the curve illustrating the effective phase-shift decreases for higher irradiance. Thus, we believe that the saturation of the effective NL refractive index is due to free-carriers generation inside the liquid. Indeed, the NL losses appear at the same intensities where the saturation of n 2eff occurs, as it can be seen by comparing Figs. 2 and 4, corroborating this interpretation.

Fig. 3
figure 3

(Color online): The effective phase variation as a function of the incident intensity. The green circles (red stars) are the results for 532 nm (1064 nm). The dotted vertical lines show the intensities for which the NL losses become relevant

Full size image
Fig. 4
figure 4

(Color online): The measured effective NL refraction coefficient in toluene at 532 nm (green circles) and 1064 nm (red stars) as a function of the intensity. The solid and the dashed lines are the fitting at relatively low intensity in order to obtain n 2 and n 4 values

Full size image

Figure 4 summarizes the results of the measured effective NL refractive indices n 2eff versus I 0, the laser intensity. n 2eff for toluene at both wavelengths increases with a relatively moderate intensity before saturation. Below the intensity threshold for plasma formation, we observe that n 2eff increases linearly with intensity. Such linear dependence indicates that high-order susceptibilities are contributing to the response of the tested material and that the contribution of the fifth-order is important even at these moderate NL phase-shifts (<π). The corresponding NL index n 4 is positive because its sign depends on the third harmonic frequency of the incident light with respect to the resonances of the medium [17]. The straight lines drawn in Fig. 4 represent the fitting using \( n_{{2{\text{eff}}}} = n_{2} + n_{4} I_{0} \), a relation valid when the NL absorption is negligible which is the case for the considered data (see Fig. 3). The fitting to the experimental data give \( n_{2} = \left( {7.7 \pm 1.5} \right) \times 10^{ - 20} {\text{ m}}^{ 2} / {\text{W}} \) and \( n_{4} = \left( {4.5 \pm 1.3} \right) \times 10^{ - 35} {\text{ m}}^{ 4} / {\text{W}}^{ 2} \) for λ = 1064 nm; at λ = 532 nm we obtained \( n_{2} = \left( {1.8 \pm 0.4} \right) \times 10^{ - 19} {\text{ m}}^{ 2} / {\text{W}} \) and \( n_{4} = \left( {5.2 \pm 1.5} \right) \times 10^{ - 34} {\text{ m}}^{ 4} / {\text{W}}^{ 2} \). The obtained n2 values here are in very good agreement with the measurement published in [18] using spectral shearing interferometry with 100-femtosecond pulses at 800 nm and low repetition rate (20 Hz). Note that the intensities used were in the range of 8.5–33 GW/cm2 which is comparable with our experimental conditions.

From 9 × 1014 W/m2 to 15 × 1014 W/m2 at 1064 nm and between 2 × 1014 W/m2 and 3 × 1014 W/m2 at 532 nm, the NL losses are not strong enough to be measured, while the saturation of Kerr effect involves higher-order NL susceptibilities where the reliability of the measurement is poor when considering the thin sample approximation.

Generally, when considering a response up to the fifth-order nonlinearity [19], under the same hypothesis of the previous subsection, the optical intensity I(W/m2) and the NL phase-shift, denoted by \( \varphi = \Delta \varphi_{\text{NL}} \) for readability, satisfy the equation:

$$ \frac{{{\text{d}}\varphi }}{{{\text{d}}z^{'} }} = k\left( {n_{2} I + n_{4} I^{2} } \right), $$
(3)

where \( k = 2\pi /\lambda \), \( n_{ 2} \) (m2/W) is the third-order refractive index, and \( n_{4} \) (m4/W2) is the fifth-order refractive index. Of course, if we consider the linear UV–Visible absorption spectrum of toluene that ends at 276 nm, NL absorption due to two-photon transition could occur at 532-nm incident wavelength. At 1064 nm, four-photon transition is required to match the absorption spectrum. However, the experimental acquisitions do not show any apparent “valley” in the open-aperture Z-scan profiles for intensities below the saturation limit defined previously. Increasing the incident intensity in order to increase the depth of the valley when compared to the noise of the normalized transmittance, self-focusing may occur inside the cell and the signal due to losses in the induced plasma because of the beam collapse takes over the signal due to NL absorptions. This observation indicates that the related C N coefficients are negligible, anyway under the experimental detection limit of the setup which is estimated to be around \( q_{0,\lim } = C_{2} LI_{0} = 0.2 \). For instance, considering the intensity level where the plasma appears at 532 nm, a rough estimation shows that \( C_{2} < {{q_{0,\lim } } \mathord{\left/ {\vphantom {{q_{0,\lim } } {\left( {LI_{0} } \right)}}} \right. \kern-0pt} {\left( {LI_{0} } \right)}} \approx 3 \times 10^{ - 13} {\text{ m/W}} \) which is a very low value. Under these conditions, Eq. 3 is solved giving the expression of the NL phase-shift:

$$ \varphi = k\left( {n_{2} I + n_{4} I^{2} } \right)L. $$
(4)

The BWRV data and the simulation of the D4σ Z-scan profile are shown in Fig. 5 for two incident intensities below the NL absorption level in the green and in the IR.

Fig. 5
figure 5

(Color online) (a) BWRV versus z for a 2-mm cell filled with toluene measured at \( \lambda = 532{\text{ nm}} \) with \( I_{0} = 1.7 \times 10^{14} {\text{W/m}}^{ 2} \)(empty circles in green) and \( \lambda = 1064{\text{ nm}} \) with \( I_{ 0} = 1.09 \times 10^{15} {\text{ W/m}}^{ 2} \) (stars in red). The solid (green) and dashed (red) lines are the simulation according to Eq. 4 using the measured values of n 2 and n 4

Full size image

The green solid line is the simulation using Eq. 4 obtained with the measured NL parameters: \( n_{2} = 1.8 \times 10^{ - 19} {\text{ m}}^{ 2} / {\text{W}} \) and \( n_{4} = 5.2 \times 10^{ - 34} {\text{ m}}^{ 4} / {\text{W}}^{ 2} \) in the absence of NL absorption. The red dashed line was obtained from the simulation with \( n_{2} = 7.7 \times 10^{ - 20} {\text{ m}}^{ 2} / {\text{W}} \) and \( n_{4} = 4.5 \times 10^{ - 35} {\text{ m}}^{ 4} / {\text{W}}^{ 2} \). The BWRV theoretical profiles show very good agreement with the experimental ones validating our approach for all the acquisitions where the absorption is insignificant as the one shown in Fig. 5. However, because the thin sample approximation was used, the values for the NL parameters may be over-estimated due to the self-focusing which increases the effective irradiance while the beam propagates inside the sample. We estimated this increase, in the worst case, at 532 nm using an input intensity of \( 2 \times 10^{14} {\text{ W/m}}^{ 2} \) (before the NL absorption appears) by performing numerical resolution of a NL Schrödinger-type equation (see Ref. [7] for details). From the increase of the output intensity after 2-mm propagation in toluene, we can conclude that the value of the average irradiance along the sample is underestimated for about 45 % in this extreme case. Taking into account this average irradiance values for intensity lower than 2 × 1014 W/m2 in the green and 9 × 1014 W/m2 in the IR, the fitting lines drawn in Fig. 4 give an estimation of the NL parameters related to toluene summarized in Table 1. This correction is not significant for n2 at both wavelengths and for n4 in the IR, but the n4 value in the green is about 60 % lower, although remaining in the same order of magnitude as before. Note that when the absorption becomes high at about 3 × 1014 W/m2 in the green (where is situated the steep variation of C 3 due to plasma generation) the values of n 2eff and C 3 become noisy. Probably also, self-focusing becomes important contributing to higher irradiance inside the material and to higher rate of plasma generation. When the electron density becomes large due to ionization, the NL properties of the medium cannot be described by a Taylor expansion of the polarization density as a power series of the field amplitude (susceptibility model) any more. Above some intensity level, free-carriers are generated and the saturation of the effective Kerr nonlinearity is mainly due to the plasma response. This is indeed known as an important mechanism inducing a negative change in the NL refractive index limiting the self-focusing action [9]. Assuming that self-focusing is limited by multiphoton excitation, the change of the slope in the effective phase which is visible in Fig. 3 for both wavelengths (vertical lines at about 14 × 1014 W/m2 for the IR and 3 × 1014 W/m2 for the green) is due to partial canceling of the Kerr effect.

Table 1 Estimated nonlinear refraction coefficients of toluene, at 532 and 1064 nm in the picosecond regime for intensities lower than 2 × 1014 W/m2 in the green and 9 × 1014 W/m2 in the IR (column 2 and 3)
Full size table

3.3 NL absorption and multiphoton ionization

Figure 6 shows an example of the open-aperture Z-scan normalized transmittance measured with the 2-mm-thick cell of toluene. The black filled circles display the experimental data obtained at 532 nm for \( I_{0} = 5.6 \times 10^{14} {\text{ W/m}}^{ 2} \), where I 0 is the focal (at z = 0) on-axis peak intensity at t = 0. As already mentioned, the object is 1.4 mm radius approximately circular aperture defining the shape and the width of the absorption “valley.” The sample thickness was smaller than the confocal parameter of the focused laser beam. The (blue) dashed dotted line represents the second-order NL absorption fitting according to Eq. 2 with \( C_{2} = \left( {1.2 \pm 0.3} \right) \times 10^{ - 12} {\text{m}} {\text{W}}^{ - 1} \). The (red) dashed line represents the third-order fitting with \( C_{3} = \left( {1.0 \pm 0.4} \right) \times 10^{ - 26} {\text{m}}^{ 3} \,{\text{W}}^{ - 2} \). The (green) solid line is the fourth-order fitting for \( C_{4} = \left( {7.9 \pm 4.5} \right) \times 10^{ - 41} {\text{m}}^{ 5} \,{\text{W}}^{ - 3} \), and the (black) dotted line is the fifth-order one considering \( C_{5} = \left( {5.9 \pm 4.4} \right) \times 10^{ - 55} {\text{m}}^{ 7} \,{\text{W}}^{ - 4} \). Obviously, Fig. 6 shows that the second-order fit is far from giving convincing result. Further, this conclusion is supported quantitatively: if we compute the distance between the data and the different theoretical fitting curves, it is found that this distance decreases significantly between N = 2 and N = 3. As shown in Fig. 6, for \( 3 \le N \le 5 \) the theoretical curves are very close to each other and the calculated distances remain inside the fluctuations of the normalized transmission. From Eq. 2, one can easily show that: \( {{\Delta C_{N} } \mathord{\left/ {\vphantom {{\Delta C_{N} } {C_{N} }}} \right. \kern-0pt} {C_{N} }} = \left( {N - 1} \right){{\Delta C_{2} } \mathord{\left/ {\vphantom {{\Delta C_{2} } {C_{2} }}} \right. \kern-0pt} {C_{2} }} \) indicating that the precision of the measurement decreases with N. Hence, as the order of the NL losses increases, it becomes more and more difficult to determine it unambiguously even if the data are close to the fittings. Moreover, the observed valley could be the result of higher-order NL absorption by the free-carriers generated at the relatively high intensities used. Although Fig. 6 suggests that the order of the nonlinearity is higher than 5, since the accuracy of the measurement is not sufficient for \( N \ge 4 \) we consider that the third-order fitting is quite acceptable and suitable to describe the experimental observations. Then the C3 parameter is expected to account phenomenologically for the effective NL losses, including MPA and other loss phenomena in the sample, although is unlikely that three-photon absorption occurs here.

Fig. 6
figure 6

(Color online): Open-aperture Z-scan normalized transmittance at 532 nm. The black filled circles represent the experimental data. The (blue) dashed dotted line represents the second-order NL absorption fitting. The (red) dashed, (green) solid and (black) dotted lines represent the third-, fourth-, and fifth-order fitting, respectively

Full size image

Indeed, assuming that all the NL losses correspond to multiphoton ionization at the lowest order and approximating the spectrum of toluene as two electronic bands separated by an energy gap, the coefficient \( C_{N} \) can be estimated by means of Keldysh theory [15, 20]. The MPA coefficient \( \beta_{m} \) is defined by

$$ \frac{{{\text{d}}N_{\text{e}} }}{{{\text{d}}t}} = \beta_{\text{m}} \left( {I_{0} } \right)^{\text{m}} . $$
(5)

\( N_{\text{e}} \) is the electron density and m the order of the MPA, if avalanche effect and relaxation are neglected. Here I 0 is the maximum internal intensity. To estimate \( \beta_{\text{m}} \) we considered the sample as a solid with E g = 4.5 eV (corresponding to 276 nm, obtained from the absorption spectrum of toluene). Then \( \beta_{\text{m}} \) is given by

$$ \beta_{\text{m}} = \frac{\omega }{9\pi }\left( {\frac{{m_{\text{r}} \omega }}{\hbar }} \right)^{{\frac{3}{2}}} \left[ {\frac{{\exp \left( 2 \right)q^{2} }}{{8\omega^{2} m_{\text{r}} c\varepsilon_{0} n_{0} E_{\text{g}} }}} \right]^{\text{m}}, $$
(6)

where c is the speed of light in vacuum, ω the angular frequency, q the elementary charge, \( m_{\text{r}} = 0.5m_{\text{e}} \), the electron reduced mass (\( m_{\text{e}} \) the electron mass), \( \hbar \) is the Planck’s constant, \( \varepsilon_{0} \) the dielectric permittivity in vacuum. \( n_{0} \) is the linear index and \( E_{\text{g}} \) the band gap energy. Measurement of the UV transmission spectrum of toluene gives a value of 276 nm for the wavelength corresponding to \( E_{\text{g}} \). The order of the photoionization is \( m = 1 + E\left[ {{{E_{\text{g}} } \mathord{\left/ {\vphantom {{E_{\text{g}} } {\hbar \omega }}} \right. \kern-0pt} {\hbar \omega }}} \right] \) where E[] holds for the integer part function. Computation gives \( m = 2 \) and \( \beta_{2} = 1.6 \times 10^{7} {\text{mW}}^{ - 2} {\text{s}}^{ - 1} \) at 532 nm, \( m = 4 \) and \( \beta_{4} = 1.6 \times 10^{ - 27} {\text{m}}^{ 5} {\text{W}}^{ - 4} {\text{s}}^{ - 1} \) at 1064 nm. Straightforward analysis shows that when assuming the NL absorption entirely due to m-photon, excitation process described by \( \beta_{m} \), the m-photon absorption coefficient is then expressed as \( C_{\text{m}} = \beta_{\text{m}} {{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } m}} \right. \kern-0pt} m} \), which yields \( C_{2} = 3 \times 10^{ - 12} {\text{m/W}} \) at 532 nm and \( C_{4} = 7.4 \times 10^{ - 47} {\text{m}}^{ 5} / {\text{W}}^{ 3} \) at 1064 nm. While the value measured in the green is of the same order than the estimated one by Keldysh theory, in the IR the measured value is much higher. The reasons for this discrepancy are multiple. On the one hand, Keldysh theory is in principle valid in solids presenting a well-defined energy gap only. On the other hand, it can be thought that, at these wavelengths, NL losses processes other than two- or four-photon ionization occur such as higher-order multiphoton ionization, NL losses of the generated plasma itself, other ionization processes as avalanche ionization based on a cascaded process involving transitions above 276 nm. Likely, using Z-scan, as the intensity increases while moving the sample in the focal region, all these processes and possibly other ones are progressively involved, which results in a faster increase of losses.

Moreover, a rough estimate of the density \( N_{\text{e}} \) of free electrons can be derived from the refraction measurements. The number \( N_{\text{r}} \) of toluene molecules by unit volume is straightforwardly computed from its molecular weight (about 92 g/mol) and density (866.9 kg/m3). Assuming that the change of the slope in the effective phase is due to partial canceling of the Kerr effect which is visible in Fig. 3 for both wavelengths (vertical lines at about 1.4 × 1015 W/m2 for the IR and 0.3 × 1015 W/m2 for the green), the generation of free-electrons as given by the Drude approximation induces a negative change in the index of refraction that becomes noticeable when the electron density satisfies [9]:

$$ N_{\text{e}} = \frac{{2\varepsilon_{0} n_{0} {\text{cm}}_{e} \omega }}{{q^{2} L}}\phi_{{0{\text{eff}}}} . $$
(7)

Taking into account the values of \( \phi_{{0{\text{eff}}}} \) (vertical lines in Fig. 3) in the green (~3.5 rad) and in the IR (~2.1 rad) the calculation gives \( N_{\text{e}} = 1.7 \times 10^{24} {\text{m}}^{ - 3} \); i.e., the proportion of ionized molecules is \( {{N_{\text{e}} } \mathord{\left/ {\vphantom {{N_{\text{e}} } {N_{\text{r}} }}} \right. \kern-0pt} {N_{\text{r}} }} = 3 \times 10^{ - 4} \), and \( N_{\text{e}} = 0.5 \times 10^{24} {\text{m}}^{ - 3} \); i.e., \( {{N_{\text{e}} } \mathord{\left/ {\vphantom {{N_{\text{e}} } {N_{\text{r}} }}} \right. \kern-0pt} {N_{\text{r}} }} = 0.9 \times 10^{ - 4} \), for both wavelengths, respectively. This estimation gives a slightly higher density of generated plasma in the green when compared to the IR.

When taking into account the results obtained previously at both wavelengths the mean estimation of the generated free-electrons density in toluene \( N_{\text{e}} \approx 10^{24} {\text{ m}}^{ - 3} \) is of the same order of magnitude than that obtained in water [8, 21–23]. It is reasonable to assume that multiphoton excitation occurs and is largely responsible of the observed NL losses.

4 Conclusion

In the present paper, we reported on NL experiments in toluene under high irradiance at 1064 and 532 nm in the picosecond regime. We have shown that a description of the effective NL refractive index increasing linearly with the intensity is valid up to a defined limit, 2 × 1014 W/m2 in the green and about 9 × 1014 W/m2 in the IR. Above these intensities the description of the optical response in terms of NL susceptibilities is not valid. Estimation of NL refraction indices is provided and summarized in Table 1. The second- and the fourth-order indices measured below the intensity limits mentioned above are shown in second and third columns, while for higher intensities (see Table 1) NLA appears estimated in fourth column using C 3 coefficient which accounts phenomenologically for the effective total NL losses inside the sample. Notice that all measured NL refraction indices decrease with increasing wavelengths as expected following the normal dispersion behavior.

A saturation phenomenon of the NL refractive index is evidenced occurring together with high-order NL losses that can be attributed to free-carriers generation. The estimation of the free-electrons density (\( N_{\text{e}} \approx 10^{18} {\text{ cm}}^{ - 3} \)) agrees with other published results.