Optimal control for Rydberg quantum technology building blocks

Abstract

We consider a platform for quantum technology based on Rydberg atoms in optical lattices where each atom encodes one qubit of information and external lasers can manipulate their state. We demonstrate how optimal control theory enables the functioning of two specific building blocks on this platform: We engineer an optimal protocol to perform a two-qubit phase gate and to transfer the information within the lattice among specific sites. These two elementary operations allow to design very general operations like storage of atoms and entanglement purification as, for example, needed for quantum repeaters.

1 Introduction

For quantum communication over large distances, high key rates require the use of quantum repeaters [1, 2] since the noise in quantum communication scales exponentially with the length of the channel. Here, we focus on one particular possible implementation of quantum repeaters, namely one based on Rydberg atoms. A number of proposals have been made to design a quantum repeater based on Rydberg atoms: using collective Rydberg gates [3, 4], fiber-coupled cavities containing Rydberg superatoms [5] and with Rydberg atoms in optical lattices [6, 7].

The quantum repeater scheme that we want to study here is sketched in Fig. 1. Each node consists of an interface that converts flying qubits into atomic qubits and vice versa, as well as of a register that can store qubits and a bus that allows to transfer qubits between the register and the interface.

The qubit conversion can be done in two steps. The first step is to map the (atomic) qubit onto a collective state of an ensemble of Rydberg atoms (gray) [8], and the second step is to use this ensemble to create a single photon [9, 10] which can then be coupled into a fiber. The ensemble of Rydberg atoms can be used as a qubit exploiting the Rydberg blockade mechanism [11]. If all atoms of the ensemble are within one blockade radius, only one of the atoms can be excited to the Rydberg state and the dynamics is then confined to the collective ground state $|g\rangle _c=|g \ldots g\rangle$ and the superposition state $|e,{\mathbf {k}}\rangle _c=\frac{1}{\sqrt{N}}\sum _i e^{i\alpha _i}|e\rangle _i$, where the sum is over all N atoms of the ensemble, $\alpha _i$ is a known phase and $|e\rangle _i$ means that atom i is excited to some excited state $|e\rangle$ and all other atoms are in $|g\rangle$.

If the excitation is done properly, the phases $\alpha _i$ are determined by the position of the atom and the wave vector of the exciting lasers, namely $\alpha _i={\mathbf {k}}{\mathbf {r}}_i$ where ${\mathbf {k}}$ is the effective wave vector and ${\mathbf{r}}_i$ is the position of atom i. If now the population of the Rydberg state is transferred to a fast decaying state, e.g., $5p_{{1/2}}$ in $^{87}$Rb, the phase information transforms into the directionality of the collectively emitted photon [9, 12, 13]. This was demonstrated for ultracold atoms [10], but also a room-temperature implementation was proposed [14]. If the pulse that transfers the population to the fast decaying state is time-modulated, one can also manipulate the shape of the emitted photon as a function of time. By engineering a time-symmetric shape, the photon can be reabsorbed by a second ensemble of the same kind [15], e.g., located in another repeater node.

To encode an atomic qubit on the ensemble, one can map $c_0|0\rangle +c_1|1\rangle$ on the ensemble state $c_0|e,{\mathbf {k}}\rangle +c_1|e,{\mathbf {k'}}\rangle$ similar to [4, 8]. The decay of the collective state then yields a flying qubit $c_0|{\mathbf {k}}\rangle +c_1|{\mathbf {k'}}\rangle$ that can be transformed into a superposition of two photonic polarizations by linear optics as suggested by [4].

Fig. 1

Left panel Two neighboring rows in an optical lattice can serve as bus and memory: At $t=0$ the yellow qubit (e.g., an interface qubit where one can read and write information, coupled to an ensemble (gray) that does the actual conversion between atomic and flying qubits) is in state $|\psi \rangle$. We want to store $|\psi \rangle$ in the red atom without affecting the state of the other atoms in the memory. This is done by first bringing the blue atom into the state $|\psi \rangle$ via the bus operation. Then, a similar bus transformation is applied to write $|\psi \rangle$ from the blue atom onto the red atom. For readout we first prepare the bus in the ground state and then transfer $|\psi \rangle$ to the yellow atom via the blue atom. If needed we can apply entangling operations between two neighboring atoms, e.g., to entangle $|\phi _4\rangle$ and $|\phi _5\rangle$. Right panel We consider atoms as three-level atoms with two stable qubit states $|0\rangle$ and $|1\rangle$ that are coupled to a highly excited Rydberg state $|r\rangle$ by two-photon transitions with Rabi frequencies $\varOmega _0$ and $\varOmega _1$ via intermediate states that are never populated (and thus don’t appear neither in the numerical treatment nor in the graph). Atoms that are excited to the Rydberg state $|r\rangle$ interact with one another

In this article, we first present a way to implement an optimal control enabled Rydberg phase gate which is to a large extent based on the previous works of some of the authors [16, 17]. Each qubit is represented by one atom, where the two atoms are placed on neighboring sites of an optical lattice. The Rydberg phase gate can be used directly to generate entanglement. For example, if we prepare the two qubits in the ground state $|00\rangle$ and drive it to the superposition state

$$\frac{|0\rangle -i|1\rangle }{\sqrt{2}}\otimes \frac{|0\rangle -i|1\rangle }{\sqrt{2}}$$

(1)

by a local $3\pi /2$ pulse on both qubits and then apply the phase gate $U_T={\mathrm {diag}}(-1,1,1,1)$, we obtain the entangled state

$$-\frac{\left.|00\right\rangle +i\left.|01\right\rangle +i\left.|10\right\rangle +\left.|11\right\rangle }{2}$$

(2)

Another local $\pi /2$ pulse on the second qubit finally yields the Bell state

$$-\frac{|00\rangle +|11\rangle }{\sqrt{2}}.$$

(3)

We can also use the proposed phase gate together with local transformations to perform a CNOT gate that can be used for error correction, e.g., against bit flip errors [1, 18].

We further consider an optical lattice filled with one $^{87}$Rb atom per site as in the experiment of Schauß et al. [19, 20]. We present a way to move qubits around within the optical lattice which is based on the proposal [21]. Our approach, though, is based on optimal control rather than exploiting Rydberg crystals and further adapted to the quantum repeater platform requirements. This building block can be used to store qubits and move close to each other qubits that have to be linked by gates.

In particular, we want to study how optimal control theory [22] can improve these elementary quantum operations within the Rydberg quantum repeater. That is, we consider a possible implementation for the two building blocks on the optical lattice, and we define quantitatively the fidelity of the desired operations and optimize external laser pulses that control these operations.

In conclusion, the components studied here, together with an interface, enable the possibility not only to send and receive qubits in a quantum repeater node, but also to store them while waiting for more qubits, and eventually link them to perform error correction and produce high-fidelity entangled pairs shared by the neighboring nodes, the necessary fundamental ingredients to perform long-distance quantum communication.

2 Rydberg phase gate

To perform the Rydberg phase gate, two atoms—each encoding one qubit—are trapped at close distance so that by their interaction an entangling phase can be acquired [12, 16, 17, 23–28]. The qubit levels $|0\rangle$ are coupled to the Rydberg state $|r\rangle$ via a two-photon transition and $|1\rangle$ is not coupled to any other state. The interaction is thereby occurring only when both atoms are in the Rydberg state and thus can be tuned by driving the level transitions with external lasers. At the same time, the evolution matrix in the logical basis $\{\vert 00 \rangle,\vert 01 \rangle,\vert 10 \rangle,\vert 11 \rangle \}$ is always diagonal since $|1\rangle =|e\rangle$ does not couple to any other state, see Fig. 2. A maximally entangling gate requires an entangling phase of $\pi$, and such a maximally entangling phase gate is locally equivalent to the CNOT gate: Together with local operations, it allows for universal quantum circuits [34]. In the simplest form, the matrix representation of the gate in the canonical basis $\{|00\rangle,|01\rangle,|10\rangle,|11\rangle \}$ is

$$U_{T}=\begin{pmatrix} -1&&{}0&&{}0&&{}0\\ 0&&{}1&&{}0&&{}0\\ 0&&{}0&&{}1&&{}0\\ 0&&{}0&&{}0&&{}1 \end{pmatrix},$$

(4)

where the entangling phase by the factor $-1=e^{i\pi }$ is completely attached to the state $|00\rangle$. Note that the entangling phase can also be distributed over the diagonal (e.g., diag$(e^{i\pi /4},e^{-i\pi /4},e^{-i\pi /4},e^{i\pi /4})$ is also a maximally entangling phase gate) and that up to local phase transformations all these cases are equivalent [35].

Fig. 2

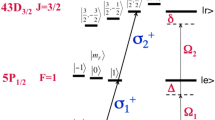
The level scheme and transitions exploited for the phase gate. The qubit is encoded by the states $|g\rangle =|0\rangle$ and $|e\rangle =|1\rangle$. The gate operation is achieved by coupling $|g\rangle$ to the Rydberg state $|r\rangle$ by a two-photon transition via the intermediate state $|i\rangle$. If both atoms are in the Rydberg state, they exhibit van der Waals interaction, contributing the entangling term $H_I=u|rr\rangle \langle rr|$ to the Hamiltonian

The Rydberg phase gate goes back to a proposal of Jacksch et al. [23] who suggested two pulse sequences to construct the gate: One for the limit of high interaction where the phase is acquired by the fact that the interaction blockades the excitation of $|00\rangle$ to the double Rydberg state $|rr\rangle$ and another sequence for the limit of small interaction where the excitation is not affected by the interaction but the state $|rr\rangle$ acquires the entangling phase due to the interaction energy. The first scheme has been demonstrated experimentally by [24, 26, 27], and a slightly different scheme leading to a CNOT gate has been demonstrated [25, 28] as well. Optimal control offers a way to access also the case when none of the two limits strictly holds [16, 17].

2.1 Implementation

We propose an implementation of the Rydberg gate similar to the experimental setup of [24, 26, 27] and similar to the previous gate proposals [29–33], and especially [17]. In the experiments, $^{87}$Rb atoms are trapped by optical tweezers. Alternatively, the atoms could also be trapped by magnetic microtraps on atom chips [16, 36]. Instead, here we consider two sites of an optical lattice as possible in the experiments [19, 20, 37]. Each atom encodes two-qubit states $\vert 0 \rangle =|g\rangle = \vert 5s_{1/2}, F=2,\;M_{F}=2\rangle$ and $\vert 1 \rangle =| e\rangle = \vert 5s_{1/2}, F=1,\;M_{F}=1 \rangle$. Additionally the ground state $|0\rangle$ is coupled to the Rydberg state $|r\rangle =|43s\rangle$ via a two-photon transition making use of the intermediate level $|i\rangle = \vert 5p_{3/2}\rangle$, see Fig. 2. We consider the qubit states to be stable while the excited states’ lifetimes are $\tau _r = 42.3\,{\mathrm {\mu s}}$ for $|r\rangle$, and $\tau _i=26.2\,$ns for $\vert i\rangle$ [38].

We study a simplified case where we neglect the loss from the intermediate level. This can be realistic, e.g., when high laser powers and detunings allow to adiabatically eliminate the intermediate level [39]. Under the rotating wave approximation, the local Hamiltonian reads

$$\begin{aligned} H_{\text {loc}}=&\frac{\varOmega _R(t)}{2}(|g\rangle \langle i| +|i\rangle \langle g|) + \frac{\varOmega _B(t)}{2}(|i\rangle \langle r| +|r\rangle \langle i|)\nonumber \\&+\delta _\mathrm{{gi}} |i\rangle \langle i| + \delta _{ir} |r\rangle \langle r|, \end{aligned}$$

(5)

where $\varOmega _{R}(t)$, $\delta _\mathrm{{gi}}$ are the Rabi frequency and detuning for the transition from $|g\rangle$ to $|i\rangle$ and $\varOmega _B$, $\delta _{ir}$ for the transition from $|i\rangle$ to $|r\rangle$, respectively.

The two atoms exhibit van der Waals interaction when both atoms are excited to the Rydberg state:

$$ H_\mathrm{{int}}=-\frac{C_6}{a^6}|rr\rangle \langle rr| $$

(6)

with a the distance between the atoms and $C_6=-1.697 10^{19}\,$au [38]. If we put the atoms on an optical lattice with lattice spacing $a=0.532\,{\mathrm {\mu m}}$ as in the experiments [19, 20], this translates into

$$ H_\mathrm{{int}}=u|rr\rangle \langle rr| $$

(7)

with $u=108.15\,h\,{\mathrm {GHz}}$. The total Hamiltonian (summing the local Hamiltonian over atoms $j=1,2$ and including the interaction between the two atoms) then reads

$$ H=\sum _j H_{\text {loc}}^{(j)} + H_\mathrm{{int}}. $$

(8)

2.2 Quasi-adiabatic gate

We now parametrize the laser pulse by four parameters: The detunings $\delta _\mathrm{{gi}}$ and $\delta _{ir}$ and the maximum Rabi frequencies $\varOmega _{R,0}$ and $\varOmega _{B,0}$, where we choose the red laser to have Gaussian shape

$$ \varOmega _R(t) = \varOmega _{R,0} \;e^{-\left( \frac{t-T/2}{\tau }\right) ^2}, $$

(9)

with total time T and $\tau = 0.2T$, while we set $\varOmega _B(t)=\varOmega _{B,0}=const$. We optimize these parameters to maximize the fidelity

$$ F=\frac{1}{16}\Bigg \vert \sum _{m,n\in \{00,01,10,11\}} \langle m|U_T^\dagger {\mathcal {U}}(T)|n\rangle \Bigg |^2\, $$

(10)

where ${\mathcal {U}}(t)$ is the time evolution of the system that depends on the control parameters. The parameters are then optimized by the Nelder–Mead simplex method [40] yielding a Fidelity $F=0.9996$ with the parameters $\varOmega _{R,0}=2\pi \cdot 332.45\,\text {MHz}$, $\varOmega _{B,0}=2\pi \cdot 323.6\,\text {MHz}$, $\delta _\mathrm{{gi}}=2\pi \cdot 1063.58\,\text {MHz}$ and $\delta _{ir}=0$. Figure 3 shows the resulting populations of the electronic levels for the optimal pulse. We can clearly see that the gate operates deep in the blockade mode where the doubly excited Rydberg state $|rr\rangle$ is never populated. The population transfer from the ground state to the excited states and back thereby allows for the relative phases to be built up. Also the population of the intermediate level $|i\rangle$ is very small which justifies the omission of the finite lifetime of the state.

Now we could go one step further and include the motion of the atoms in the trap. This increases the operation error due to a spreading of the wave function and random phases due to the motion of the atoms in the laser field. We can also consider the finite lifetimes of $|i\rangle$ and $|r\rangle$ which decreases the fidelity due to loss, especially from the intermediate state. This has been studied in [16, 17]. Both effects decrease for shorter gate times, and it could be shown that more sophisticated optimal control techniques, namely the Krotov algorithm [22, 41–43], can lead to shorter gate times and can further suppress the loss from the intermediate state by an additional penalty term in the control objective [16].

Fig. 3

The population of the electronic levels for ${\mathcal {U}}(t)|gg\rangle$ (left panel) and ${\mathcal {U}}(t)|ge\rangle$ (right panel). The population is smoothly transferred from the ground state to the Rydberg state and back down. A two-qubit phase is accumulated by the interaction while the atoms are excited. Note that ${\mathcal {U}}(t)|eg\rangle$ is not shown for symmetry reasons and ${\mathcal {U}}(t)|ee\rangle$ is not coupled to the other levels

3 Rydberg quantum bus

Rubidium atoms on an optical lattice as achieved in the experiment of [19, 20, 37] (with one atom per site and single addressing) can be used to encode one qubit per atom, that is, one qubit per lattice site. We can use this optical lattice as a quantum memory equipping the optical lattice with an interface that allows input and output of information, e.g., via photon emission and absorption, and if we are also able to transport a quantum state from the interface to any desired atom on the lattice. Furthermore, if we want to entangle two qubits, we can move them to neighboring sites of the lattice and apply our phase gate (which is universal together with local transformations [28]) to complete the requirements of the quantum repeater node.

The interface is discussed in Introduction (in this case several lattice sites form one such ensemble as needed for the interface), and the phase gate is discussed in the previous section. Here we want to analyze the transport of a quantum state to a desired site via a Rydberg quantum bus. This was first discussed by Weimer et al. [21] using a crystalline phase of the bus and adiabatic excitation schemes. Here we present an optimal control version tailored especially for the purpose of this quantum repeater building block.

3.1 The effective $2^N$ level system

The setup is described more in detail in Figs. 1 and 4. For our calculations, we consider thus a chain of N atoms with two levels each, namely $|g\rangle =|0\rangle$ and $|r\rangle$. We drive the transition between the two levels with a laser—technically this could be a two-photon transition as in the previous section where this time the lasers are far off-resonant from the intermediate level so that it can be adiabatically eliminated [39]—while there is also a nonlocal contribution to the Hamiltonian due to the two-body interaction between excited atoms:

$$ H=\sum _i H_{\text {loc}}^{(i)} + \sum _{i\ne j} H_\mathrm{{int}}^{(i,j)}\,$$

(11)

where the local Hamiltonian due to the laser driving with Rabi frequency $\varOmega _0(t)$ and detuning $\Delta$ in the RWA is

$$ H_{\text {loc}}^{(i)}=\frac{\varOmega _0(t)}{2}(|g_i\rangle \langle r_i| +|r_i\rangle \langle g_i|)+\Delta |r_i\rangle \langle r_i|. $$

(12)

If we choose $|r\rangle =|43s\rangle$, we have van der Waals interaction between the atoms i and j:

$$ H_\mathrm{{int}}^{(i,j)}=-\frac{C_6}{r_{ij}^6}|r_i r_j\rangle \langle r_i r_j| $$

(13)

with $r_{ij}$ the distance between the atoms and $C_6=-1.697 10^{19}\,$au [38]. If we put the atom on an optical lattice with lattice spacing $a=0.532\,{\mathrm {\mu m}}$ as in the experiments [19, 20] for an atom on site i and an atom on site j of a chain, this translates into

$$ H_\mathrm{{int}}^{(i,j)}=-\frac{\tilde{C}_6}{|i-j|^6}|r_i r_j\rangle \langle r_i r_j| $$

(14)

with $\tilde{C}_6= -108.15\,h\,{\mathrm {GHz}}$.

We choose the Rabi frequency $\varOmega _0$ to be of the order of a few GHz and the detuning $\Delta$ to be a few hundred MHz. The total time is set to $T=10\,$ns.

Fig. 4

Atoms on an optical lattice. By addressing only certain atoms by the exciting lasers, we can restrain the dynamics to a specific 1D chain of atoms within the optical lattice (gray): We first transfer all the population from $|1\rangle$ to $|r\rangle$ by a fast $\pi$-pulse on $\varOmega _1$ (only addressing atoms in the chain; see Fig. 1 for the level scheme) and then on this chain work on the space $|0=g\rangle$, $|r\rangle$ where the transition is driven by $\varOmega _0$. Interaction between two atoms only takes place when both atoms are in the Rydberg state $|r\rangle$, and thus interaction takes place only for atoms in the chain. After the operation a fast $\pi$-pulse on the atoms in the chain transfers the population from $|r\rangle$ back to $|1\rangle$

3.2 The control task

Our control target is described in Fig. 5. At $t=0$ we start from a product state $|\psi \rangle \otimes |g\rangle \otimes \dots \otimes |g\rangle =\vert \psi \rangle \otimes \vert G \rangle$ (where we introduce the shorthand $\vert G \rangle =\vert g \rangle \otimes \dots \otimes \vert g \rangle$ to denote a $(n-1)$-sites state with all sites in the ground state $\vert g \rangle$) and want to transfer this state to the final time product state $|\Psi \rangle \otimes |\psi \rangle$. Hereby $|\psi \rangle$ represents the qubit that we want to store at the last site of the chain and $|\Psi \rangle$ represents the state of the rest of the chain after the operation.

Fig. 5

Bus operation. At $t=0$ the yellow atom is in state $|\psi \rangle$, while the rest of the bus is prepared in the ground state $|g\rangle$. We want to transfer the state $|\psi \rangle$ to the blue atom by an optimal laser pulse on the atoms. At $t=T$, after the application of the pulse, the blue atom is in state $|\psi \rangle$. This bus operation can be constructed for bridging the distance between 1 to 6 atoms with high fidelity. We distinguish between two approaches depending on the final state of the rest of the bus. First, the rest of the bus is in the ground state after the transfer to be ready for the next operation (upper panel). Note that during the bus operation though the atoms in the bulk can be excited. Second, the rest of the bus is in an unknown state which has to be cooled down to the ground state before the next operation (lower panel)

It is useful to realize the bus in such a way that the chain gets restored to the ground state, i.e., $|\Psi \rangle =\vert G \rangle$, so that afterward the next bus operation can immediately be performed without cooling the system back to the ground state (see upper panel in Fig. 5). For that case to work for any $|\psi \rangle$, we choose the fidelity of our operation as

$$ F_1=\frac{1}{4}\left |\langle g|\otimes \langle G| {\mathcal {U}}(T)\vert G \rangle \otimes |g\rangle + \langle r|\otimes \langle G \vert {\mathcal {U}}(T)\vert G \rangle \otimes \vert r \rangle \right |^2\,. $$

(15)

Note that this operation disregards the global phase but preserves the relative phase between $|g\rangle$ and $|r\rangle$.

However, sometimes it might not be necessary to put such a narrow constraint on the bus operation, and we can treat $|\Psi \rangle$ to be any kind of state not entangled with the state of interest $|\psi \rangle$ on the last site (see lower panel in Fig. 5). In other words, we want

$$ {\mathcal {U}}(T)\vert \psi \rangle \otimes \vert G \rangle \mathop {=}\limits ^{!}\vert \Psi \rangle \otimes \vert \psi \rangle, $$

(16)

or with $\vert \psi \rangle =\alpha \vert g \rangle +\beta \vert r \rangle$ we want

$$ \alpha {\mathcal {U}}(T)\vert g \rangle \otimes \vert G \rangle \mathop {=}\limits ^{!}\alpha \vert \Psi \rangle \otimes \vert g \rangle,$$

(17)

$$ \beta {\mathcal {U}}(T)\vert r \rangle \otimes \vert G \rangle \mathop {=}\limits ^{!}\beta \vert \Psi \rangle \otimes \vert r \rangle.$$

(18)

Introducing the raising operator $(|r\rangle \langle g|)_n=I\otimes \dots \otimes I\otimes \vert r \rangle \langle g \vert$ on the last site, the first condition reads

$$\alpha (|r\rangle \langle g|)_n{\mathcal {U}}(T)\vert g \rangle \otimes \vert G \rangle \mathop {=}\limits ^{!}\alpha \vert \Psi \rangle \otimes \vert r \rangle. $$

(19)

Now these conditions can be recast into the fidelity

$$F_2={\mathfrak{R}}(\langle r | \otimes \langle G | {\mathcal{U}}^{\dagger}(T) (|r\rangle \langle g |)_n {\mathcal{U}}(T)| g \rangle \otimes | G \rangle), $$

(20)

where taking the real part ensures phase preservation between $\vert g \rangle$ and $\vert r \rangle$. After such an operation $|\Psi \rangle$ can be cooled down to the ground state by dissipative dynamics.

3.3 Results

For the transfer of the state $|\psi \rangle$, we simulate the time dynamics using matrix product states and Trotter time steps [44, 45]. We use bond dimensions of 2, 4 and 8 for 2, 4 and 6 particles, respectively, and 10000 Trotter time steps. The single operators were applied by multiplying matrices on the MPS sites, the interaction by a combination of site swapping (to bring two interacting sites close to each other), contracting one link (to create a two-body tensor) and applying the two-body operator on this tensor. We then use the simulation to optimize the driving laser field $\varOmega _0(t)$ and the constant detuning $\Delta$ with the chopped random basis (CRAB) algorithm [46, 47]. This algorithm uses a truncated basis of trigonometric functions to represent the optimal driving pulse. This way the infinite-dimensional optimal control problem transforms into a low-dimensional one where the coefficients are optimized by the Nelder–Mead simplex method.

A recent extension, the dCRAB algorithm [48], improves the convergence of the algorithm by iteratively applying CRAB—each times with a different truncated basis and building up on the current best pulse. The trigonometric basis functions can then be bandwidth-limited by choosing frequencies out of an interval $[0,\omega _\mathrm{{max}}]$ where the classical channel capacity of the control pulse (i.e., the information contained in the pulse) has to be adapted to the dimensionality D of the control problem as $\omega _{\ rm {max}} T\ge D$ [48, 49].

For the optimization of the Rydberg quantum bus for each single run of CRAB, we used 10 frequencies to modulate the shape of $\varOmega _0(t)$ as well as $\Delta$ as an additional parameter to be optimized by the Nelder–Mead simplex method. In the following, we show results achieved for different lengths of the quantum bus including 2, 4 or 6 sites. The bandwidths we used are of $\omega _\mathrm{{max}}=40\cdot 2\pi /T$ for 2 and 4 sites and $\omega _\mathrm{{max}}=160\cdot 2\pi /T$ for 6 sites. First, we perform the optimization using the fidelity $F_1$ shown in Eq. 15.

We can see the transfer of the Rydberg state $|r\rangle$ from the first site to the final site of the atom chain in Fig. 6 (the transfer of $|g\rangle$ is not shown but behaves in a similar way). For the transfer of the state from one site to its neighbor or to the fourth site, high fidelities of $F_1>0.99$ could be achieved in the proposed time of $10\,$ns. The shape of the transfer for 2 sites implies that a faster transfer would also be possible with a very high fidelity.

Fig. 6

To illustrate the transfer operation, we show how the state $|\psi \rangle =|r\rangle$ is transferred over the bus. The graphs show the population p(t) of the Rydberg state for the first site of the chain (yellow) and the target site (blue) for 2 sites (left panel), 4 sites (middle panel) and 6 sites (right panel). The results were obtained by maximizing $F_1$

For the transfer to the sixth site of the chain, we see a drop of the fidelity down to about 95 % in the right panel of Fig. 6. The reason for this might be that the pulse time is not long enough for the state to be transferred, i.e., that the proposed time is below the quantum speed limit [50]. In Fig. 7, we see the result for a six-particle transfer in $40\,$ns. The additional time made it possible to achieve a transfer fidelity of about 98%. The pulse for the laser field is shown in the right panel of Fig. 7.

Fig. 7

Left panel The population p(t) of the Rydberg state for the first site (yellow) and at the last site (blue) for the 6 sites chain and an operation time of $40\,$ns is illustrated for the basis state $|\psi \rangle =|r\rangle$. Right panel The shape of the corresponding driving laser field $\varOmega _0(t)$ that maximizes $F_1$

The previous results have shown that we can perform a fast state transfer using the Rydberg quantum bus. But we were working with the limitation that after the operation we return to the ground state ready to start the next transfer. This limitation leads to the fact that we had to increase the transfer time in order to achieve good fidelities for a six-site transfer.

But, as we show in Fig. 8, lifting this constraint and using the fidelity $F_2$ defined in Eq. 20 allows for better results of the optimization. On the left panel in Fig. 8, we see the state transfer of the Rydberg state $|r\rangle$ for 6 sites in only $10\,$ns. As we see in comparison with Fig. 6, the state transfer could be improved drastically to a fidelity well above 99%. The corresponding pulse for the driving laser field is shown in the right panel of Fig. 8. The absolute laser power remains below $2\,$GHz throughout the pulse keeping it to a regime that is well accessible for lasers used in current experimental setups. In an actual experiment, however, the bandwidth of the pulse could cause problems that we will just discuss shortly in this purely theoretical article. The bandwidth of the pulse in Fig. 8 is about $\omega _\mathrm{{max}}=2\pi \cdot 16\,$GHz which is problematic in two ways: Firstly, standard electro- or acousto-optical modulators allow only for a bandwidth of a few hundred MHz (nanosecond timescale). Secondly, also the model for the Hamiltonian breaks down at this high frequencies, since, for example, the two ground states are separated only by $6.83\,$MHz [51]. Luckily, there is a way to overcome this problem. One obvious way is to scale down the Rabi frequency by a factor $\alpha$ and scale up the operation time by the same factor $\alpha$, while the distance between the atoms is scaled up by a factor $\alpha ^{1/6}$ to adjust the van der Waals interaction to the smaller Rabi frequencies. Furthermore, we need such high frequencies in the control field to put enough information into the system to perform the system operation [48, 49]. However, we can put the same information into the system by using multiple control fields with a lower bandwidth each. For example, if we time-modulate not only the Rabi frequency, but also the phase and the detuning of the control pulse, we can encode the same amount of information with one third of the bandwidth. The ultimate limit is given by the inequality [49]

$$n_c \omega _\mathrm{{max}}T\ge D,$$

(21)

where $n_c$ is the number of control fields and D is the (real) dimension of the system space (in the case of 6 qubits $D=128$). In this way, we can estimate that for the mentioned three independent controls and an operation time of $100\,$ns we enter the experimentally accessible range.

Summarizing, we could provide a method for a fast quantum bus using Rydberg atoms. The protocol obtained by maximizing $F_1$ returns the involved sites to the ground state after the transfer allowing another operation just when the previous one has finished. This constraint, though, reduces the achievable fidelity of the transfer. Higher fidelities in shorter times are achieved if an explicit ground-state cooling step is introduced and the more flexible fidelity $F_2$ is introduced.

Fig. 8

Left panel The population p(t) of the Rydberg state for the first site (yellow) and at the last site (blue) for the 6 sites chain and an operation time of $10\,$ns illustrated for the basis state $|\psi \rangle =|r\rangle$. Right panel The shape of the driving laser field $\varOmega _0(t)$ that maximizes the fidelity $F_2$

4 Conclusions

We have designed Rybderg quantum repeater elements on an optical lattice with special focus on the entangling gate operation and the transport of qubit states within a quantum memory platform. Both processes were optimized with optimal control tools. Under optimal conditions, the gate can be achieved with $99.96\,\%$ fidelity. Analogously, we studied two different methods to achieve qubit transport, demonstrating how pulses with higher bandwidth and a more flexible control objective could increase the distance bridged by the transport operation. In conclusion, we have presented an approach to enabling the fundamental operations to implement a Rydberg atom quantum repeater infrastructure compatible with current experimental setups which we hope will be experimentally implemented in the near future.