1 Introduction

In physics, the classical harmonic oscillator is one of the fundamental model systems. Despite its simplicity, it captures the essence of resonance phenomena occurring in a variety of systems, such as in mechanical oscillators, in electrodynamic integrated circuits, or in the absorption and scattering of light of an atom or a molecule. Although for these systems the harmonic oscillator often constitutes a lowest order approximation, for example for small amplitudes, the model very well describes the main features of the response to external stimuli.

Another system that recently attracted a lot of attention and that also exhibits harmonic oscillations are plasmonic nanoantennas [1–5]: When light close to a resonance impinges on a metal nanoantenna, collective oscillations of the conduction electrons can be excited, so-called localized surface plasmons. At resonance, the electron oscillation causes enhancement of the absorption and scattering of light as well as the local electric fields [6, 7]. The latter in particular is interesting for boosting nonlinear optical effects at the nanoscale [8–10]. Hence, in recent years scientists searched for different complex plasmonic nanostructure geometries, such as dipole and bow-tie nanoantennas [11–14], T- or L-shaped structures [15–18], split-ring-resonators [19–22], plasmonic oligomers [23, 24], and hybrid dielectric plasmonic nanostructures [25–27], to boost second-harmonic or third-harmonic (TH) generation. In these nonlinear optical effects, two or three incoming photons are combined and upconverted to one outgoing photon at two or three times the incoming energy, respectively.

In this Letter, we investigate in detail the polarization-resolved linear and TH optical response of two orthogonally coupled plasmonic oscillators [28, 29]. We find that despite the complexity of the nanostructures and the corresponding electrodynamic processes, the linear and the TH response can be described and understood by a classical coupled oscillator model. This model not only describes the polarization-resolved lineshapes of the linear and the nonlinear response, but also explains the relative TH intensities and the phase behavior for excitation and TH emission under different polarization directions.

2 Linear optical response of coupled plasmonic oscillators

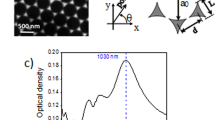
To experimentally investigate the optical response of coupled plasmonic nanoantennas, we fabricated gold nanostructure arrays with an area of \(100 \times 100\, \mathrm {\upmu m}^2\) on a fused silica substrate. The unit cell of the arrays consists of two orthogonally coupled gold nanorods. In Fig. 1, corresponding tilted scanning electron micrographs are shown. The nominally identical gold nanorods have a length, width, and height of about 220, 60, and \(40\, \mathrm {nm}\), respectively, and the gap distance, which describes the shortest distance between the two gold nanorods, is on the order of about \(10\, \mathrm {nm}\). The lattice constant in both directions is \(600 \, \mathrm {nm}\).

Fig. 1
figure 1

Scanning electron micrographs of the investigated plasmonic nanoantenna array, which consists of orthogonally coupled gold nanoantennas on a fused silica substrate. The scale bar is 500 and \(100\, \mathrm {nm}\) in the overview and the inset, respectively. In the upper left, the coordinate system used in the manuscript is shown (\(\mathbf {E}\): polarization vector of the external electric field, \(\beta\): angle between the x-axis and the external electric field)

Full size image

Owing to the small distance between the nanorods, the plasmonic modes can exchange energy via their optical near-fields. Hence, the plasmonic modes couple, hybridize, and form two new eigenmodes at lower and higher energies [30].

When shining light polarized at an angle \(\beta\) of \(+45^{\circ }\) or \(-45^{\circ }\) (see Fig. 1) under normal incidence onto the nanoantenna array, the higher or lower energy eigenmode is excited. The resulting plasmonic mode features a symmetric or antisymmetric charge oscillation with a phase difference of the two antennas of 0 or \(\pi\), respectively.

In contrast, if the incoming light polarization is oriented at an arbitrary angle \(\beta\), in particular also along one of the nanorods (\(\beta = 0^{\circ }\)), the resulting oscillation will be a superposition of the two eigenmodes. In the particular case when \(\beta\) is equal to \(0^{\circ }\), the phase between the plasmonic modes of the two antennas varies with excitation wavelength and increases from 0 to \(\pi\) with decreasing excitation wavelength, and corresponds to \(\pi /2\) at the resonance frequency \(\omega _0\) of the two antennas.

Fig. 2
figure 2

a Simulated absorbance spectra of the coupled plasmonic oscillator nanoantenna array for excitation along \(0^\circ\), \(-45^\circ\), and \(+45^\circ\). b, c Simulated surface charge density distributions \(\sigma\) on the surface of the gold nanoantennas as well as simulated electric field distributions \(E_z\) of the z-component of the electric field in a plane \(5\, \mathrm {nm}\) below the nanostructures for excitation along \(-45^\circ\) (b) and \(+45^\circ\) (c), respectively

Full size image

To illustrate the modes of the coupled plasmonic oscillators and to predict the linear optical response of the nanostructures, we performed finite element simulations using Comsol Multiphysics. In the simulations we utilized the geometrical parameters from above, the substrate has been modeled with a constant refractive index of \(n = 1.45\), and for the optical properties of gold we used the data of Johnson and Christy [31]. The resulting simulated absorbance spectra for excitation at \(\beta\) equal to \(-45^{\circ }\), \(+45^{\circ }\), and \(0^{\circ }\) are shown in Fig. 2a. As expected for excitation at \(-45^{\circ }\) and \(+45^{\circ }\), we observe two distinct eigenmodes, whereas for \(0^{\circ }\) excitation an equal superposition of these modes is excited. In Fig. 2b, c, simulated surface charge density distributions and electric field distributions for excitation of the lower and higher energy eigenmode are shown, each plotted at their corresponding spectral peak position marked in Fig. 2a.

By comparing the simulated absorbance spectra to the experiment, we can see that these predict the optical response of the plasmonic nanoantenna arrays precisely. However, the main features can be described by a classical coupled oscillator model, and we will see that this simple model allows to gain unexpectedly deep insight into the origin of the linear and nonlinear response.

2.1 Harmonic coupled oscillator model

In the following, we develop such an oscillator model in detail. At first, we consider the linear optical response and hence neglect anharmonicities in the differential equations. They will be introduced later as a small perturbation to account for the third-order response.

The equations of motion of two identical coupled harmonic oscillators are

$$\begin{aligned}&\ddot{x}^{(0)} + 2 \gamma \dot{x}^{(0)} + {\omega _\mathrm {0}}^2 x^{(0)} + \kappa y^{(0)} = -\frac{e}{m} E_x(t) \end{aligned}$$
(1)
$$\begin{aligned}&\ddot{y}^{(0)} + 2 \gamma \dot{y}^{(0)} + {\omega _\mathrm {0}}^2 y^{(0)} + \kappa x^{(0)} = -\frac{e}{m} E_y(t), \end{aligned}$$
(2)

where

\(x^{(0)}, y^{(0)}\) :

are the amplitudes of the two plasmonic modes oriented along the x- and y-direction, respectively,

\(\gamma\) :

is a damping constant,

\(\omega _0\) :

is the resonance frequency of the uncoupled oscillators,

\(\kappa\) :

describes the coupling strength of the two oscillators, which is mediated by the electric near-fields of the antennas,

e :

is the charge of the oscillators,

m :

is the mass of the oscillators, and

\(E_x, E_y\) :

are the cartesian components of the incident electric field.

The solution to the coupled equations (1, 2) is most easily found by Fourier transformation. In frequency space and matrix notation, the two equations read

$$\begin{aligned} \underbrace{ \begin{bmatrix} 1/g&\kappa \\ \kappa&1/g \\ \end{bmatrix} }_{M} \underbrace{ \begin{bmatrix} x^{(0)}(\omega )\\ y^{(0)}(\omega )\\ \end{bmatrix} }_{\mathbf {x}^{(0)}(\omega )} = - \frac{e}{m} \underbrace{ \begin{bmatrix} E_x (\omega ) \\ E_y (\omega ) \\ \end{bmatrix} }_{\mathbf {E}(\omega )}, \end{aligned}$$
(3)

where \(g = - 1 /(\omega ^2 - \omega _0^2 + 2 i \gamma \omega )\) is the linear response function of an individual oscillator.

To solve the system of equations (3), one can either invert the oscillator matrix M or transform to the normal coordinates \(\mathbf {x}_n^{(0)}\) of the system, in which the matrix M exhibits only nonzero values on the diagonal. The latter case also directly delivers the eigenmodes of the system. The corresponding transformation is carried out here, using the ansatz \(\mathbf {x}^{(0)} = Q \mathbf {x}_n^{(0)}\), where Q is an orthogonal transformation matrix, and by multiplication of equation (3) with the inverse of Q [32]:

$$\begin{aligned} \underbrace{Q^{-1} M Q}_{M_n} \mathbf {x}_n^{(0)}&= - \frac{e}{m} \underbrace{Q^{-1} \mathbf {E}}_{\mathbf {E}_n} \end{aligned}$$
(4)
$$\begin{aligned} \Rightarrow \mathbf {x}_n^{(0)}&= - \frac{e}{m} M_n^{-1} \mathbf {E}_n \end{aligned}$$
(5)

Here, \(M_n=Q^{-1} M Q\) and \(\mathbf {E}_n = Q^{-1} \mathbf {E}\) are the oscillator matrix M and the external electric field \(\mathbf {E}\) represented in the normal mode coordinate system, respectively. To determine these quantities, we calculate the eigenvalues \(\lambda\) of the matrix M, which are given by

$$\begin{aligned} \lambda _l = \frac{1}{g} - \kappa&= - (\omega ^2 - (\omega _0^2 - \kappa ) + 2 i \gamma \omega ) \end{aligned}$$
(6)
$$\begin{aligned} \lambda _h = \frac{1}{g} + \kappa&= - (\omega ^2 - (\omega _0^2 + \kappa ) + 2 i \gamma \omega ), \end{aligned}$$
(7)

where the indices l and h denote the lower and higher energy eigenmode. The eigenvalues show that we obtain new eigenfrequencies at \(\omega _l = \sqrt{\omega _0^2 - \kappa }\) and \(\omega _h = \sqrt{\omega _0^2 + \kappa }\). Furthermore, the corresponding normalized eigenvectors point in the direction of \(\mp 45^{\circ }\) and can be calculated as \(\mathbf {u}_l = 1/\sqrt{2} [1;-1]\) and \(\mathbf {u}_h = 1/\sqrt{2} [1;1]\). The eigenvectors \(\mathbf {u}_{l,h}\) allow to calculate the transformation matrix \(Q = [\mathbf {u}_l, \mathbf {u}_h]\), and the eigenvalues \(\lambda _{l,h}\) determine the oscillator matrix \(M_n\) in the normal mode coordinate system:

$$\begin{aligned} M_n= \begin{bmatrix} \lambda _l&0 \\ 0&\lambda _h \\ \end{bmatrix} = \begin{bmatrix} 1/g_l&0 \\ 0&1/g_h \\ \end{bmatrix}, \end{aligned}$$
(8)

Here, \(g_l\) and \(g_h\) correspond to the linear response function of the lower and the higher energy eigenmode, and exhibit the same functional behavior as the linear response function g of the original oscillators, except that the resonance frequency \(\omega _0\) has to be replaced by the corresponding eigenfrequency \(\omega _{l,h}\).

To link our model to optically measurable quantities, we relate the electric polarization \(\mathbf {P}_n\) similar to the Drude–Lorentz model to the oscillator amplitudes \(\mathbf {x}_n^{(0)}\) within the normal mode coordinate system by

$$\begin{aligned} \mathbf {P}_n&= \epsilon _0 \chi _{_n}^{(1)} \mathbf {E}_n = - e N \mathbf {x}_n^{(0)} = \frac{e^2 N}{m} M_n^{-1} \mathbf {E}_n&\end{aligned}$$
(9)
$$\begin{aligned}&\Rightarrow \quad \chi _{_n}^{(1)} = \frac{e^2 N}{\epsilon _0 m} M_n^{-1} = \frac{e^2 N}{\epsilon _0 m} \begin{bmatrix} g_l&0 \\ 0&g_h \\ \end{bmatrix} , \end{aligned}$$
(10)

where N is the number density of the plasmonic oscillators. Furthermore, we introduced the first-order susceptibility tensor \(\chi _{_n}^{(1)}\), which is directly related to the inverse of the oscillator matrix \(M_n\), and therefore also only has diagonal elements.

Fig. 3
figure 3

Measured (colored) and modeled (yellow dashed) absorbance spectra for different angles \(\beta\) of the incoming polarization direction

Full size image

Ultimately, the absorbance spectra A for light polarized along the coordinate axes are related to the imaginary part of the diagonal components of the susceptibility tensor \(\chi _{_{n;ii}}^{(1)}\) (\(i=1,2\)) [33]:

$$\begin{aligned} A \propto \omega \cdot {\text {Im}}\left\{ \chi _{_{n;ii}}^{(1)}\right\} \end{aligned}$$
(11)

2.2 Linear optical spectroscopy

To experimentally determine the linear optical response of the orthogonally coupled plasmonic oscillators and to test the validity of our model, we measured the transmittance spectra T and the reflectance spectra R of the sample under normal incidence for various polarization angles \(\beta\) ranging from \(-45^{\circ }\) to \(+45^{\circ }\) and calculated via \(A=1-R-T\) the corresponding absorbance spectra A, which are depicted in Fig. 3. Furthermore, to determine the parameters for the oscillator model we used the derived formulas for the absorbance spectra for excitation at \(\beta\) equal to \(-45^{\circ }\) and \(+45^{\circ }\) as fitting functions for the corresponding measured absorbance spectra. Subsequently, the absorbance spectra for excitation at arbitrary polarization directions \(\beta\) can be obtained by rotating the susceptibility tensor \(\chi _{_{n}}^{(1)}\) to the corresponding coordinate system using an appropriate rotation matrix. The resulting modeled absorbance spectra are shown together with the corresponding measured absorbance spectra in Fig. 3, where we find an excellent agreement.

Hence, the coupled plasmonic oscillator model captures the linear optical response of the investigated plasmonic nanoantenna array conclusively. In the following, we will extend this model to the anharmonic regime, which becomes important when high-intensity ultrashort laser pulses are focused onto the nanoantenna arrays.

3 Third-order optical response of coupled plasmonic oscillators

As the external light field increases in intensity, the harmonic approximation of the last section does no longer describe the optical response of the coupled plasmonic oscillators in a satisfactory fashion. At high light intensities, nonlinear optical effects appear that are not accounted for in the harmonic approximation.

However, second-order nonlinear optical effects vanish in the bulk of centrosymmetric media, and hence, the second-order response of the coupled plasmonic oscillators is weak compared to the third-order one, for which there are less symmetry restrictions [34, 35]. In fact, in the nonlinear experiments described below we also observe a distinct second-harmonic response, which we find to be about an order of magnitude weaker when compared to the measured TH signal intensities. Hence, the strongest contribution to the nonlinear optical response of the coupled plasmonic oscillators is governed by a third-order optical nonlinearity, leading to strong TH generation.

3.1 Anharmonic coupled oscillator model

In order to describe the third-order response of the coupled plasmonic oscillators, we include in the coupled differential equations anharmonic terms, which are proportional to the third power of the amplitudes x(t) and y(t) of the plasmonic oscillators [12, 25, 35–37]:

$$\begin{aligned} \ddot{x} + 2 \gamma \dot{x} + {\omega _\mathrm {0}}^2 x + \kappa y + a x^3&= -\frac{e}{m} E_x(t) \end{aligned}$$
(12)
$$\begin{aligned} \ddot{y} + 2 \gamma \dot{y} + {\omega _\mathrm {0}}^2 y + \kappa x + a y^3&= -\frac{e}{m} E_y(t) \end{aligned}$$
(13)

Here, we introduced the anharmonicity parameter a, which describes the overall strength for third-order nonlinear optical effects. This parameter is assumed to be identical for the two polarizations, since the two orthogonally oriented antennas are nominally fabricated with identical geometrical parameters. As long as this parameter is small, i.e., the anharmonic contribution in equations (12, 13) is small compared to the other terms, it is possible to solve the coupled differential equations using perturbation theory [35]. Hence, we express the amplitudes as power series for the perturbation parameter a as

$$\begin{aligned} x&= x^{(0)} + a x^{(1)} + \mathcal {O}(a^2) \end{aligned}$$
(14)
$$\begin{aligned} y&= y^{(0)} + a y^{(1)} + \mathcal {O}(a^2), \end{aligned}$$
(15)

where \(x^{(0)}\) and \(y^{(0)}\) are the original unperturbed amplitudes of the plasmonic oscillators and \(x^{(1)}\) and \(y^{(1)}\) are the first-order corrections which describe the third-order response. When we insert the ansatz (14, 15) into the differential equations (12, 13) and compare terms of the same power of the perturbation parameter a, we find in zeroth order (\(a^0\)) as expected the linear coupled differential equations (1, 2) from the previous section. In first-order perturbation theory (\(a^1\)), we obtain:

$$\begin{aligned} \ddot{x}^{(1)} + 2 \gamma \dot{x}^{(1)} + {\omega _\mathrm {0}}^2 x^{(1)} + \kappa y^{(1)}&= - (x^{(0)}(t))^3 \end{aligned}$$
(16)
$$\begin{aligned} \ddot{y}^{(1)} + 2 \gamma \dot{y}^{(1)} + {\omega _\mathrm {0}}^2 y^{(1)} + \kappa x^{(1)}&= - (y^{(0)}(t))^3 \end{aligned}$$
(17)

The equations take the same form as equations (1, 2), yet, they are modified by a source term proportional to the cubed unperturbed amplitudes \(x^{(0)}\) and \(y^{(0)}\). This shows in a descriptive fashion that the plasmonically enhanced near-field amplitudes \(x^{(0)}\) and \(y^{(0)}\) drive the TH conversion [14].

As before, to solve the coupled differential equations we transform to the frequency domain, which leads to

$$\begin{aligned} \underbrace{ \begin{bmatrix} 1/g&\kappa \\ \kappa&1/g \\ \end{bmatrix} }_{M} \underbrace{ \begin{bmatrix} x_1(\omega )\\ y_1(\omega )\\ \end{bmatrix} }_{\mathbf {x}^{(1)}(\omega )} = - \mathcal {F} \begin{bmatrix} (x^{(0)}(t))^3 \\ (y^{(0)}(t))^3 \\ \end{bmatrix}, \end{aligned}$$
(18)

where \(\mathcal {F}\) describes a Fourier transform. In contrast to the linear optical case, the transformation of equation (18) to the normal mode coordinate system is not possible in a straightforward and satisfactory fashion. The right-hand side depends nonlinearly on the original plasmonic modes \(\mathbf {x}^{(0)}(t)\), and hence, after a coordinate transformation the equation will still show this nonlinear dependency of \(x^{(0)}(t)\) and \(y^{(0)}(t)\). This once more underlines that the original plasmonic modes \(\mathbf {x}^{(0)}\), and in particular not the normal modes \(\mathbf {x}_n^{(0)}\), drive the TH conversion. Therefore, this time we remain in the original coordinate system and obtain the solution for the TH amplitudes \(\mathbf {x}^{(1)}\) using a matrix inversion:

$$\begin{aligned} \begin{bmatrix} x^{(1)} \\ y^{(1)} \\ \end{bmatrix} = - \underbrace{ \frac{1}{1 - \kappa ^2 g^2} \begin{bmatrix} g&-\kappa g^2 \\ -\kappa g^2&g \\ \end{bmatrix} }_{M^{-1}} \mathcal {F} \begin{bmatrix} (x^{(0)}(t))^3 \\ (y^{(0)}(t))^3 \\ \end{bmatrix} \end{aligned}$$
(19)

The various matrix components of the inverse oscillator matrix \(M^{-1}\) describe different physical processes, which we would like to discuss briefly.

First, in the diagonal components we find the TH amplitudes weighted with the linear response function g. Unfortunately, the gold nanorods do not exhibit a plasmonic resonance at the TH frequency, and hence, in the TH spectral range the linear response function g is close to zero and spectrally flat. Hypothetically, if the nanorods exhibited also a plasmonic resonance at the TH frequency, this term could efficiently enhance the TH emission, as recently shown by several publications about two-photon- or doubly resonant plasmonic structures [24, 38–40].

Furthermore, the non-diagonal components describe the transfer of TH energy from one gold nanorod to the other. Therefore, the amplitudes are weighted with a factor of \(-\kappa g^2\). Here, the response function g enters once for the plasmonic nanorod at which the TH is generated and once for the nanorod to which it is transferred to, while the coupling coefficient \(\kappa\) accounts for the overall efficiency of the TH energy transfer.

As a reminder, the response function g at the TH frequency is small and spectrally flat, and as a result the absolute values of the non-diagonal components \(|\kappa g^2|\) are much smaller than the absolute values of the diagonal components |g|. Hence, TH energy transfer between the two plasmonic oscillators described by the non-diagonal components is negligibly small. Furthermore, the linear response function g and the pre-factors of the inverse matrix \(M^{-1}\) are at the TH spectrally flat. Therefore, the TH amplitudes \(x^{(1)}(\omega )\) and \(y^{(1)}(\omega )\) are in good approximation simply proportional to the Fourier transforms of \((x^{(0)}(t))^3\) and \((y^{(0)}(t))^3\). Finally, the x- and y-polarized TH electric field amplitudes \(E_{x,y}^{(1)}\) radiated to the far-field can be calculated by \(E_{x}^{(1)} \sim i\omega \cdot x^{(1)}\) and \(E_{y}^{(1)} \sim i\omega \cdot y^{(1)}\), respectively [41].

Fig. 4
figure 4

Experimental setup for TH spectroscopy: LMA-PCF large mode area photonic crystal fiber, SM silver mirror, AM aluminum mirror, AL achromatic lens, FL fused silica lens, S sample, A analyzer, and KG Schott KG filters

Full size image

3.2 Third-harmonic spectroscopy

In order to test whether the classical oscillator model is able to describe the TH response of the coupled plasmonic oscillators, we perform polarization-resolved TH spectroscopy. The corresponding experimental setup is shown in Fig. 4. We utilize a homebuilt Yb:KGW solitary mode-locked oscillator emitting \(175\, \mathrm {fs}\) laser pulses at a repetition rate of \(44\, \mathrm {MHz}\) and a central wavelength of \(1030\, \mathrm {nm}\) [42]. The oscillator laser pulses are sent into a nonlinear photonic crystal fiber for spectral broadening and subsequently into a 4f pulse shaper for amplitude and phase modulation. This setup allows to generate sub-\(30\, \mathrm {fs}\) laser pulses tunable from 900 to \(1180\, \mathrm {nm}\) [43]. For the TH spectroscopy experiments, the laser pulses from the pulse shaper are focused onto the sample under normal incidence using a 75-mm focal length achromatic lens with an average power of about \(15\, \mathrm {mW}\). The sample itself is mounted onto a rotation holder so that it can be rotated around the axis parallel to the propagation direction of the laser light; hence, effectively the light polarization is rotated with respect to the plasmonic oscillators. Subsequently, we collimate the TH signals radiated in forward direction using a fused silica lens, send the signals through an analyzer, filter the fundamental laser light using a stack of KG5 filters, and measure the TH signals with a Peltier-cooled CCD camera attached to a spectrometer. Following to the measurements, we integrate the TH spectra over all wavelength components to obtain a scalar value describing the TH intensity. Lastly, to eliminate the influence of the wavelength dependence of the optical components in the experimental setup, we normalize all TH signals from the nanostructures to TH signals generated at a 20-nm-thick gold film [14, 20].

Fig. 5
figure 5

Experimental (a) and modeled (b) absorbance spectra as well as polarization-resolved TH spectra plotted over the fundamental excitation wavelength. The top axis shows the corresponding TH wavelength. The first and second row depict the results for excitation under \(+45^\circ\) and \(-45^\circ\), respectively, while the third and fourth row depict the results for excitation under \(0^\circ\), but with different output polarizations of the TH light, namely along \(0^\circ\) and \(90^\circ\) as well as \(\pm 45^\circ\), respectively

Full size image

3.3 Results and discussion

The results of the TH spectroscopy experiments and the corresponding modeled spectra using the anharmonic coupled oscillator model are shown in Fig. 5a, b, respectively.

In the first row, the absorbance spectrum for excitation of the higher energy eigenmode, i.e, for the incident light polarization being parallel to \(+45^{\circ }\) (cyan), is shown, as well as the corresponding TH spectra, which were measured and modeled for an analyzer angle of \(-45^{\circ }\) (magenta) and \(+45^{\circ }\) (cyan). We find the TH signals polarized parallel to the fundamental laser light peaking close to the higher energy mode resonance frequency \(\omega _h\). Furthermore, perpendicular to the incoming polarization direction very weak TH signals are detected. The TH signals found in this polarization direction in the experiment can most likely be attributed to small structure imperfections and alignment uncertainties of the analyzer and the rotation angle of the sample.

Furthermore, in the second row we show the absorbance spectrum for excitation at \(-45^{\circ }\) as well as the corresponding polarization-resolved TH intensities. As before, we find a pronounced TH signal in the polarization direction which is oriented parallel to the fundamental exciting laser polarization, and it peaks close to the excited lower energy eigenmode resonance frequency \(\omega _l\). Remarkably, the peak of the TH generation efficiency is for the excitation at \(-45^{\circ }\) by about a factor of two stronger when compared to the excitation at \(+45^{\circ }\), which will be discussed below (note the different scaling of the TH intensity axis).

Hence, we find that when an eigenmode of the coupled system is excited, the TH signals at frequency \(3\omega\) exhibit the same light polarization as the fundamental exciting laser light at frequency \(\omega\). The origin for this polarization behavior can be easily understood: Since the TH near-field amplitudes \(x^{(1)}\) and \(y^{(1)}\) are proportional to the cubed fundamental amplitudes \(x^{(0)}\) and \(y^{(0)}\), the TH amplitudes exhibit the same symmetric or antisymmetric oscillatory behavior when one of the eigenmodes is excited.

In the third row, the results for excitation at \(\beta\) equal to \(0^{\circ }\) (black) together with the corresponding TH spectra, which were measured at a TH polarization angle \(\beta\) of \(0^{\circ }\) (green) and \(+90^{\circ }\) (orange), are shown. The TH spectrum polarized parallel to the exciting laser light exhibits two peaks due to the excitation of the two eigenmodes. Furthermore, nonlinear polarization conversion of the TH can be observed, which is caused by efficient transfer of energy at frequency \(\omega\) to the perpendicularly oriented nanorod and by a subsequent TH generation at this nanorod. We find this perpendicularly polarized TH to peak in between the two eigenmodes and close to the original resonance frequency \(\omega _0\), as reproduced by the model.

Finally, in the fourth row the polarization angle \(\beta\) of the incident laser light still is equal to \(0^{\circ }\); however, the radiated TH signals are analyzed in the polarization directions of the eigenmodes, at \(-45^{\circ }\) (magenta) and \(+45^{\circ }\) (cyan). Most interestingly, in the two TH spectra two spectral positions which lie symmetrically around \(\omega _0\) can be identified, at which one of the two TH polarization components approaches zero intensity. Hence, here the TH is purely polarized in the corresponding perpendicular eigenmode polarization direction.

The reason for this polarization behavior can be comprehended by realizing that the phase between the two plasmonic oscillators varies in the TH by \(3\pi\) when the laser is spectrally tuned over the resonance, rather than over \(\pi\) as in case of the fundamental field: In the fundamental field, the phase between the two plasmonic oscillators \(\Delta \varPhi _{xy}\) amounts to \(\pi /2\) at the resonance frequency \(\omega _0\) of the plasmonic nanorods, i.e., at the dip between the two eigenmodes. Furthermore, at slightly shorter and longer wavelength this phase difference will acquire \(\pi /3\) and \(2\pi /3\). Hence, in the TH the phase difference at these spectral positions will be \(\pi\) and \(2\pi\), corresponding to an antisymmetric and a symmetric TH oscillation, respectively.

Remarkably, the modeled TH spectra shown in Fig. 5b display all features of the linear and the TH response. In particular, the lineshape of the TH spectra is modeled in a precise fashion. Furthermore, the relative TH signal strength can be predicted, since all depicted TH spectra are scaled with only one global parameter relative to the measured ones. This fact also allows to understand the higher efficiency for TH generation of the lower energy eigenmode: A lower eigenfrequency corresponds to a reduced restoring force of the plasmonic oscillation, which leads to a higher effective field enhancement and hence to more efficient generation of TH light [27].

4 Conclusion

To summarize, we investigated the linear and the TH response of plasmonic nanoantenna arrays that consist of orthogonally coupled gold nanorods. We find that a classical anharmonic coupled oscillator model is able to capture almost all features of the linear and the nonlinear optical response. In particular, we find that when an eigenmode of the coupled plasmonic system is excited, no nonlinear polarization conversion takes place. In contrast, when a superposition is excited, TH energy efficiently can be converted to the perpendicular polarization direction. Furthermore, the interference of the generated TH signals from both nanorods shows that the phase difference in the TH near-field amplitudes varies over \(3\pi\) when the laser is spectrally tuned over the resonance, rather than over \(\pi\) as in the case of the fundamental field.

We believe that this work extends the understanding of the ultrafast nonlinear optical processes in plasmonic nanostructures and hence can pave the way toward applications in the field of more complex nonlinear plasmon optics.