Site-selective measurement of relaxation properties at 980 nm in Er$^{3+}$-doped congruent and stoichiometric lithium niobate crystals

Abstract

A pump-probe-type saturation spectroscopic experiment has been performed at 980 nm to measure the homogeneous linewidth of the $^4$I$_{11/2}$–$^4$I$_{15/2}$ transition and the lifetime of the $^4$I$_{11/2}$ state of erbium embedded into lithium niobate single crystals. There are several non-equivalent Er$^{3+}_{\mathrm{Li}^+}$–V$_{\mathrm{Li}^+}$ sites with differently oriented defect structure for charge compensation. These non-equivalent centers differ in their transition energies. Hence, our measurements have been done at two nearby frequencies, addressing groups of erbium ions located at non-equivalent sites. The results are compared with lifetime calculations and measurements found in the literature and with the predictions of our simple model calculation.

1 Introduction

Recently, several coherent quantum optical processes were studied in erbium (Er$^{3+}$)-doped dielectric crystals: The primary motivation of choosing Er$^{3+}$ dopant ions is that it’s $^4$I$_{13/2} \leftrightarrow ^4$I$_{15/2}$ transition is resonant with the frequency of the telecommunication laser field with wavelength ~1.5 μm. In order to achieve coherent quantum dynamics in an atom/ion driven by an external light field, a long dephasing time associated with the transition under consideration is of paramount importance. Several crystals have been tested as a host of erbium dopants to find long coherence time in the telecommunication wavelength range [1]. Even for a given host crystal, the concentration of the dopant ions, the temperature of the sample, and the applied external magnetic field influence significantly the value of the coherence time. Among others, there are detailed studies to explore these effects in Y$_2$SiO$_5$:Er$^{3+}$ [2–4], and in LiNbO$_3$:Er$^{3+}$ [5].

The coherent quantum dynamics in the dopant erbium ions induced by an infrared light field has many applications, ranging from diode laser frequency stabilization [6], electromagnetically induced transparency [7], ultraslow light propagation via coherent population oscillations [8], control of dispersion and group velocity [9], interference of spontaneous emission of light from two solid-state atomic ensembles [10], and optical quantum memories [11–15].

Besides the telecommunication wavelength range, there are some other wavelength ranges which have proved to be relevant in practical applications. One of them is the near infrared (NIR) range between 980–1100 nm: the ytterbium-doped crystal and fiber lasers radiate in the wavelength range 1030–1080 nm and may be pumped with ~980 nm light. There are several optical devices optimized to this wavelength domain. The $^4$I$_{11/2} \leftrightarrow ^4$I$_{15/2}$ transition of the trivalent erbium ion is resonant with the NIR light of wavelength $\sim$980 nm. Therefore, we choose to study the quantum mechanical coherence time of erbium embedded into lithium niobate crystals (erbium-doped lithium niobate, LiNbO$_3$:Er$^{3+}$). As a NIR light source, we used a diode laser tuned to $\approx$980 nm. In a previous paper [16], we have reported the homogeneous linewidth and population relaxation time measurements in ytterbium-doped lithium niobate crystals. The excitation wavelength was also around 980 nm.

The paper is organized as follows: In Sect. 2, the optical spectra of erbium-doped lithium niobate is discussed. Then in Sect. 3 the physical background of our model calculation is presented. The results of our measurements are shown in Sect. 4. Some conclusion is drawn in Sect. 5.

2 The optical spectra of sLN/cLN:Er

The energy levels of Er$^{3+}$ (4$f^n$ ion with n = 11) in congruent LiNbO$_3$ were first determined by Gabrielyan et al. [17] at T = 77 K. They identified the Stark levels due to crystal field splitting from the $^4$I$_{15/2}$ ground state up to the $^4$G$_{11/2}$ manifold in the ultraviolet. Dierolf and Koerdt [18] studied the optical transitions of Er$^{3+}$ ions in stoichiometric LiNbO$_3$ crystals prepared from congruent one by the vapor transport equilibration technique. From our laser-spectroscopic point of view, the $^4$I$_{11/2}$ excited level at about 970–980 nm is of great importance. Figure 1 shows the absorption spectra of congruent and stoichiometric LiNbO$_3$:Er$^{3+}$ crystals at $T = 9$ K. At this temperature, only the lowest energy level of the $^4$I$_{15/2}$ ground state is occupied; hence, the absorption spectra reveal only the split of the $^4$I$_{11/2}$ excited level. Er$^{3+}$ ions occupy Li$^{+}$ sites in LiNbO$_3$ crystals with C₃ symmetry, as concluded from the results of several techniques such as X-ray standing waves (XSW) [19], extended X-ray fine structure (EXAFS) [20], X-ray absorption and wide angle X-ray scattering spectroscopy [21], Rutherford back-scattering (RBS) [22] and electron paramagnetic resonance (EPR) spectroscopies [23–25]. Thus the $^4$I$_{11/2}$ excited level splits into six components in the crystal field, as shown in the figure in agreement with earlier observations [17, 18]. It is clearly seen, however, that the absorption bands related to the six components are broader and less resolved for congruent crystal than for stoichiometric one. Such effect has been observed for most of the spectroscopic signals in LiNbO$_3$ and is generally attributed to the higher disorder present in the congruent crystal [26]. Despite the more ordered structure of stoichiometric LiNbO$_3$ the six lines of the $^4$I$_{11/2}$ level further split as shown for the lowest $^4$I$_{11/2}$ level at about 10,200 cm$^{-1}$ in the inset of Fig. 1. Site-selective spectroscopic measurements attributed this splitting to Er$^{3+}$ ions located in Li$^{+}$ sites with differing arrangements of their local charge compensation [27–29]. Differently oriented Er$^{3+}_{\mathrm{Li}^{+}}$–V$_{\mathrm{Li}^+}$ complexes have been identified by the EPR technique [23].

Fig. 1

Absorption spectra of the $^4$I$_{15/2}$ $\leftrightarrow$ $^4$I$_{11/2}$ transition of Er$^{3+}$ in cLN:Er (red, solid) and sLN:Er (blue, dashed) crystals measured at $T = 9$ K. The inset shows the split of the lowest energy excited level due to the occupation of non-equivalent sites by Er$^{3+}$ ions

3 Physical model

The Hamiltonian of the valence electrons of the dopant ions embedded into the host crystal reads

$$\begin{aligned} H_\mathrm{tot}=H_\mathrm{ion}+H_\mathrm{ion-lat}+H_\mathrm{ion-ion}, \end{aligned}$$

(1)

where $H_\mathrm{ion}$ is the triply ionized free ion Hamiltonian for f-electron ions [30, 31]; the ion-lattice interaction $H_\mathrm{ion-lat}$ includes the interaction of the valence electrons with the crystal field, and this term is responsible for the crystal field splitting [31]; the operator $H_\mathrm{ion-ion}$ describes the quasi-static interaction between the dopant ions (e.g. which cause small level shifts and splittings). The short timescale interaction between the dopant ion spins—lattice ion spins [32], and between the dopant ions—lattice phonons are treated as dephasing [33]. The Er$^{3+}$ ions have 11 valence electrons, hence in the LiNbO$_3$ crystal, the crystal field states of the dopant ions are doubly degenerate (Kramer’s degeneracy).

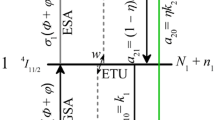
In our model calculation the Er$^{3+}$ ions are treated as three level systems: as we mentioned in Sect. 2, the crystal field splits the $^{2S+1}L_J$ states of the Er$^{3+}$ ions. The $^4$I$_{15/2}$, $^4$I$_{13/2}$, and the $^4$I$_{11/2}$ manifolds split to 8, 7, and 6 Stark-levels, respectively. The separation of the crystal field states is a few dozens of cm$^{-1}$; hence, any occupation from the higher laying crystal field states relaxes rapidly to the lowest one of the manifold via non-radiative phonon-assisted decay processes in a timescale much shorter than a nanosecond. Hence, those crystal field states which participate in a radiative decay process (and subject to phonon-assisted decay as well) can be merged to a single energy level; therefore, we can treat the Er$^{3+}$ ion as a three level system. The interaction with the external light pulses are described by a dipole interaction Hamiltonian [34]. For a complete description, dissipating effects should also be included. There are two types of dissipations: (a) population relaxation from the excited state $^4$I$_{11/2}$ and (b) dephasing of the transition dipole moment between the coherently coupled states $^4$I$_{15/2}$–$^4$I$_{11/2}$. The population relaxation from the state $^4$I$_{11/2}$ occurs in two paths: (I) a direct relaxation to the ground state; (II) in a relaxation chain through the state $^4$I$_{13/2}$ to the ground state. The (theoretical) branching ratio between the two channels is around 89:11 [35–38]. In Fig. 2, we show the relevant part of the Er$^{3+}$ energy diagram. The thick lines are the lowest levels of the crystal field level manifolds, whereas the dashed lines represent higher energy levels in the band, separated by few dozens of cm$^{-1}$ from the bottom of the band. Inside a band, the population from a higher energy level descends quickly to the bottom level via non-radiative decay mechanisms. For convenience, the relevant levels are labeled by 1,2, and 3. The population relaxation rates are denoted by $\varGamma _i$ and $\varGamma _{ij}$, so that the total population relaxation rate from state 1 is $\varGamma _1=\varGamma _{12}+\varGamma _{13}=T_1^{-1}$.

In our experiment, the coherent driving occurs between the states 1 and 3. Hence, coherence builds up only between these two states. Therefore, in the model coherence relaxation takes place only between the states 1 and 3. The associated coherence (dipole) relaxation time is denoted by $T_2$. The coherence relaxation time is related to the homogeneous linewidth $\gamma _\mathrm{h}$ through the relation $\gamma _\mathrm{h}=1/(\pi \,T_2)$. The homogeneous linewidth can be decomposed to several terms on physical basis

$$\begin{aligned} \gamma _\mathrm{h} = \gamma _0+\gamma _\mathrm{ion-lat}+\gamma _\mathrm{ion-ion}+\gamma _\mathrm{ion-phon}, \end{aligned}$$

(2)

where $\gamma _0=1/(2\pi \,T_1)$ is the radiative decay rate of the ground- to excited-state coherence, this is the ultimate lowest limit of $\gamma _\mathrm{h}$. The decay rate $\gamma _\mathrm{ion-lat}$ includes the contribution from the magnetic dipole interaction between the ion spin—lattice spins. The rate $\gamma _\mathrm{ion-ion}$ originates from the dopant ion–ion interactions [41]. The last term $\gamma _\mathrm{ion-phon}$ is the contribution from the various electron–phonon processes, such as the direct one-phonon process, the two-phonon Raman process, the two-phonon Orbach process, and the multiphonon relaxation [42]. These processes are responsible for the temperature dependence of the homogeneous linewidth, although only some of them contribute significantly.

Fig. 2

The relevant part of the Er$^{3+}$ ion energy level diagram, including the radiative population relaxation paths

One can use the master equation formalism to describe the pump-probe measurement process. The pump pulse prepares a subset of the Er$^{3+}$ ions, only those ions interact significantly with the pump pulse for which the detuning from resonance is not more than a few times of the homogeneous linewidth. Right after the pump pulse ceases, the population difference between the states 1 and 3 reads

$$\begin{aligned} W(0)=P_1(0)-P_3(0)=-\frac{\delta ^2+1/T_2^2}{\delta ^2+ \frac{1}{T_2^2}+\frac{T_1}{T_2}\varOmega _\mathrm{w}^2} \end{aligned}$$

(3)

Then, a free evolution is allowed, the populations from the states $^4$I$_{11/2}$ and $^4$I$_{13/2}$ of the Er$^{3+}$ ions relax to the ground state $^4$I$_{15/2}$. It is assumed that the coherence between the lowest levels of the $^4$I$_{11/2}$ and $^4$I$_{15/2}$ manifolds decays much more rapidly than the population, which is justified by our observations. Under these conditions, the time development of the population inversion Eq. (3) can be determined by solving the rate equations for the three involved states. The resulting time-dependent population inversion between states 1 and 3 is given by

$$\begin{aligned} W(t)&=\left[ \left( \frac{2\varGamma _2}{2\varGamma _2+\varGamma _{12}}+ \frac{\varGamma _{12}\varGamma _2}{(2\varGamma _2+\varGamma _{12}) (\varGamma _2-\varGamma _1)}\right) e^{-\varGamma _1t_d}\right. \nonumber \\&\quad \left. -\frac{\varGamma _{12}\varGamma _1}{(2\varGamma _2+\varGamma _{12}) (\varGamma _2-\varGamma _1)}e^{-\varGamma _2t_d} \right] (1+W(0))-1 \nonumber \\&\equiv F(t_d)(1+W(0))-1, \end{aligned}$$

(4)

where $t_d$ is the time delay, the symbol $F(t_d)$ for the time dependence is introduced for later convenience. Finally, the interaction with the subsequent probe pulse can be calculated [16]. The susceptibility of the Er$^{3+}$-doped LN crystal for the probe pulse can be determined from the obtained density matrix elements. The result is given by

$$\begin{aligned} \chi ^+(\Delta )=&\frac{\mathcal{N}|d_{eg}|^2}{\varepsilon _0\hbar }\pi g(0) \left[ \frac{\frac{T_1}{T_2}\varOmega _\mathrm{w}^2\Delta }{\varGamma \left( (\frac{1}{T_2}+\varGamma )^2+\Delta ^2\right) } \right. \\&\left. +i\left( 1-\frac{\frac{T_1}{T_2}\varOmega _\mathrm{w}^2(\frac{1}{T_2}+\varGamma )}{\varGamma \left( (\frac{1}{T_2}+\varGamma )^2+\Delta ^2\right) }F(t_d) \right) \right], \nonumber \end{aligned}$$

(5)

where $\varGamma ^2=\frac{1}{T_2^2}+\frac{T_1}{T_2}\varOmega _\mathrm{w}^2$. The real part of $\chi ^+(\Delta )$ describes a phase shift for the probe pulse, whereas the imaginary part contributes to attenuation. For $\Delta =0$, i.e., when the pump and probe pulses have the same frequency, the attenuation is minimal. Therefore, the imaginary part of the susceptibility in Eq. (5) describes a spectral hole.

In the Eq. (5) the quantity $(T_1/T_2)\varOmega _\mathrm{w}^2$ corresponds to power broadening. For a low intensity pump (write) pulse, the result of the convolution can be expanded, in lowest order of $\varOmega _\mathrm{w}^2$ one finds

$$\begin{aligned} \text {Im}(\chi ^+(\Delta ))=\frac{\mathcal{N}|d_{eg}|^2}{\varepsilon _0\hbar } \pi g(0)\left( 1-\frac{2\frac{T_1}{T_2}\varOmega _{\mathrm{w}^2}}{\Delta ^2+\frac{4}{T_2^2}}F(t_d)\right). \end{aligned}$$

(6)

The exponential terms in $F(t_d)$ describe the vanishing of the spectral hole due to population relaxation. The angular frequency difference is defined as $\Delta = 2\pi \, \Delta '$, where $\Delta '$ is a frequency difference, which is measured directly in the experiment. Hence, the full width at half maximum of the spectral hole is $\sigma _\mathrm{sph}= 2/(\pi \, T_2)$. The homogeneous linewidth $\gamma _\mathrm{h}$ is half of the spectral hole width

$$\begin{aligned} \gamma _\mathrm{h}= \frac{\sigma _\mathrm{sph}}{2}=\frac{1}{\pi \,T_2}. \end{aligned}$$

(7)

We obtained a simple expression which relates the measured spectral hole width to the coherence relaxation time of the transition under study.

4 Experimental results

We performed a pump-probe-type saturation spectroscopic measurement, the experimental setup is essentially the same as in Ref. [16]. In this section, we present the systematically measured relaxation parameters of sLN/cLN:Er for the transition between the lowest levels of the ground $^4\mathrm{I}_{15/2}$ and the excited $^4\mathrm{I}_{11/2}$ state manifolds. The frequency of this transition is around 10,200 cm$^{-1}$. It was discussed in the introduction that the Er$^{3+}$ ions occupy non-equivalent sites in the LN host matrix, resulting in observable shift in the transition frequency. It can be seen in the inset of Fig. 1. that in sLN:Er there are three well resolved absorption peaks around 10,200 cm$^{-1}$. For one of the measured transitions, we chose the one with the highest absorption at 10,198 cm$^{-1}$. In case of the cLN:Er crystal, the fine details of this spectral line are smeared. One can fit Gaussian line profiles to reproduce the measured spectrum. The far right Gaussian is centered at 10,205 cm$^{-1}$, so it was chosen as a second transition for comparison.

4.1 Homogeneous linewidth of the $^4\mathrm{I}_{11/2}$–$^4\mathrm{I}_{15/2}$ transition at 9 K

Fig. 3

Shape of a typical spectral hole in cLN:Er. The dots are the measured values, whereas the solid curve is a fitted Lorentzian curve

In the first series of measurements, we have determined the homogeneous linewidth of the $^4\mathrm{I}_{11/2}$–$^4\mathrm{I}_{15/2}$ transition of Er in cLN and sLN at 9 K temperature. We have used Eqs. (5), (6), and (7) for evaluating the measurement results. The spectral holes were created by a long, typically 22–29 ms pulse with approximately 3–30 W/cm$^2$ peak intensity at the focal point of the focusing lens. A subsequent pulse with monotonous frequency chirp was used to scan the spectral hole, with approximately 0.4–5 W/cm$^2$ peak intensity. A typical frequency scan result is shown in Fig. 3. In contrast to our earlier measurements on sLN:Yb and cLN:Yb [16], here there is no sign of a double spectral hole structure; hence, a single Lorentzian curve was fitted to the observed spectral hole.

Fig. 4

Outcome of a typical z-scan measurement in sLN:Er: the spectral hole width is depicted as a function of lens position from sample. The power broadening is the highest at the focal point, while it vanishes far from the focus

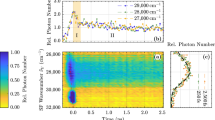
We have explained after Eq. (5) that there appears power broadening in the observed spectral hole originating from the writing pulse. We exploited this effect to estimate the weak field limit of the spectral hole width by applying the z-scan method explained in our previous work [16]. The result of a typical z-scan is shown in Fig. 4. The frequency scanning of the second pulse have been realized by the built in piezo scanner of the laser head. We inserted the estimated spectral hole widths into Eq. (7) to obtain the $T_2$ relaxation times.

Table 1 Experimental parameters for the pump-probe spectral hole width measurements

The measurements were performed for cLN:Er and for sLN:Er: the parameters of the crystal samples and the most important settings for the measurements are summarized in Table 1. Most of the parameters are self-explaining; here, we describe only three of them: Er conc. in melt (mol%): Stoichiometric LiNbO$_3$ single crystal was grown by the HTTSSG (high temperature top seeded solution growth) method, using a computer-controlled resistance heated crystal growth apparatus, from the high temperature solution containing 13.5 mol% K$_2$O, 0.05 mol% Er$_2$O$_3$ and [Li$_2$O]/[Nb$_2$O$_5$] = 1 ratio in the starting liquid. Congruent LiNbO$_3$ single crystal was grown by the Czochralski method using diameter-controlled resistance heated crystal growth apparatus from the melt of congruent composition [Li$_2$O]/[Nb$_2$O$_5$ ] = 0.9455 containing 0.05 mol% Er$_2$O$_3$. As raw materials, Starck LN grade Nb$_2$O$_5$, Merck Suprapure Li$_2$CO$_3$, and Merck p.a. K$_2$CO$_3$, Er$_2$O$_3$ 99.9 % were used. For spectroscopic measurements, z-cut samples in thickness of 1.85 mm (sLN:Er) and 1.89 mm (cLN:Er) were prepared. The amount of Er applied in the melt resulted in similar absorption coefficients for the absorption spectra of the $^4$I$_{11/2}$–$^4$I$_{15/2}$ transition in both crystals, as seen in Fig. 1. The parameter relaxation time means the time delay between the ceasing of the pump pulse and starting of the scanning pulse (blank period). No laser light falls to the sample during this time. For the piezo scanning, the blank period should be several dozens of microseconds because of the inertia of the piezo-driven grating mirror in the laser head. The parameter scanning time means the time duration of the linear voltage ramp applied to the piezo-driven frequency shifter of the laser head. However, for the piezo scanning the realized scanning time could be quite different from the scanning time which would follow from the time dependence of the driving voltage. The difference is due to the inertia and nonlinear response of the flexible mount which holds the grating. The time–frequency characteristics of the piezo scanner has been measured with a high resolution Fabry–Pérot interferometer [43]. During the evaluation of the spectral hole shapes, the frequency dependence of the absorption curves (see e.g. Fig. 3) have been corrected with the time–frequency characteristics.

We have performed a careful error analysis on the measured data to estimate the overall error of the spectral hole shape measurements: we have taken into account the accuracy of the Lorentzian fit, the estimated error due to calibration error of piezo frequency scanning, the effect of transmittance change due to laser wavelength instability. In Figs. 4, 5, and 6, the error bars represent the total estimated error. The measured homogeneous linewidths and the calculated $T_2$ relaxation times are summarized in Table 2. They are close to each other, however, the differences are larger than the measurement errors; hence, one can conclude that the Er$^{3+}$ ions at different sites exhibit perceptible difference in coherence time.

Table 2 Summary of the measured coherence relaxation times at 9 K

4.2 Lifetimes of the states $^4\mathrm{I}_{11/2}$ and $^4\mathrm{I}_{13/2}$ at 9 K

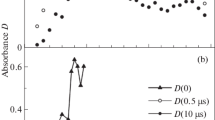
We have explained after Eq. (6) that the population relaxation rate can be estimated from the vanishing of the spectral hole. To this end, a series of spectral hole depth measurements has been performed, in which the time delay $t_d$ between the ceasing of the pump pulse and the center of probe pulse is increased. In Fig. 5, the graph of a typical lifetime measurement is shown. The beginning of the curve is slightly bent, indicating that the decay process is not purely exponential. We have fitted the sum of two exponential functions

$$\begin{aligned} F_\mathrm{fit}(t_d)=A\exp (-\varGamma _1t_d)+B\exp (-\varGamma _2t_d)+C, \end{aligned}$$

(8)

corresponding to the time dependence function $F(t_d)$ defined in Eq. (4). We have identified a fast and a slow decay process, the retrieved lifetime values for both samples are summarized in Table 3. The relative error for the fast decay process is rather high. This results from the fact that the ratio of the obtained coefficients A and B is in the range $A/B=0.09\ldots 0.21$; hence, the weight of the rapid decay is small. The ratio can be calculated by inserting our measured decay times into the expression for $F(t_d)$ defined in Eq. (4). The result is $A_\mathrm{calc}/B_\mathrm{calc}\approx 1.75$; hence, there is a large difference between theory and experiment. There are a number of papers [29, 35–38] which report theoretical predictions for the radiative lifetime of the $^4$I$_{11/2}$ and $^4$I$_{13/2}$ states of Er in LiNbO$_3$. In some cases, measured values are also published [29, 35, 36]. In Table 4. these values are summarized for comparison. Our measured fast relaxation process lifetimes are quite close to those found in fluorescence lifetime measurements for the $^4$I$_{11/2}$ level. However, the theoretical predictions are an order of magnitude longer. The difference can be well described by a multiphonon relaxation process of the excited-state electrons in the rare earth ions [39, 40]. In [35], this phenomenological theory is used to explain the temperature dependence of the Er$^{3+}$ ion excited-state lifetimes in cLN host crystal in the temperature range 5–300 K. In case of the $^4$I$_{11/2}$ state the multiphonon process correction to the radiative decay rate is given by

$$\begin{aligned} \varGamma _1=\varGamma _1^\mathrm{rad}+ \varGamma _1^\mathrm{phon}\left( \frac{\exp \frac{\hbar \omega }{kT}}{\exp \left( \frac{\hbar \omega }{kT}\right) -1 }\right) ^p, \end{aligned}$$

(9)

where $\varGamma _1^\mathrm{rad}$ is the radiative decay rate obtained from the Judd-Ofelt theory (see [35] for summary), the phonon frequency is $\omega$, k is the Boltzmann constant, T is the temperature of the crystal, p is the number of phonons in the multiphonon process. At low temperature, the above formula reduces to the form $\varGamma _1=\varGamma _1^\mathrm{rad}+\varGamma _1^\mathrm{phon}$, from which the spontaneous multiphonon transition rate $\varGamma _1^\mathrm{phon}$ can be determined by comparing the calculated radiative and measured decay rates.

Our slow lifetimes are in the same range as those found in fluorescence lifetime measurements for the $^4$I$_{13/2}$ level. Hence, we can conclude that our measurement indicates that the population decay process from the $^4$I$_{11/2}$ of Er$^{3+}$ in cLN:Er and sLN:Er is not a pure exponential decay. The influence of the intermediate $^4$I$_{13/2}$ is clearly visible. Our measured lifetime values are in good agreement with those found in time-resolved fluorescence lifetime measurements.

Table 3 Summary of the measured population lifetimes at 9 K

Table 4 Summary of lifetimes for the $^4$I$_{11/2}$ and $^4$I$_{13/2}$ states of Er in LiNbO$_3$ found in the literature

Fig. 5

Time dependence of the spectral hole depth in sLN:Er. The vertical axis is logarithmic

4.3 Temperature dependence of the homogeneous linewidth of the $^4\mathrm{I}_{11/2}$–$^4\mathrm{I}_{15/2}$ transition

We have measured the temperature dependence of the spectral hole widths too. To this end, we used the lowest intensity position of z-scan measurement described in Sect. 4.1, for increasing sample temperatures. It practically coincides with the limiting values of the z-scan curves that were accepted as spectral hole widths for vanishing power broadening effect. A typical result for sLN:Er is shown in Fig. 6. We have fitted an exponential function to the measured points, which describes the effect of thermally excited phonons (a direct one-phonon process) to the spectral hole width [42]. The characteristic energy differences for the direct one-phonon process extracted from the exponential fits both for sLN:Er and cLN:Er are listed in Table 5. In this model, the homogeneous linewidth depends linearly on the phonon occupation number, which leads to the observed exponential temperature dependence of the spectral hole width.

Fig. 6

Temperature dependence of the spectral hole width in cLN:Er

Table 5 Characteristic energy difference in the exponential function of the phonon occupation number for cLN:Er and sLN:Er.

5 Summary

We have performed a pump-probe-type saturation spectroscopic experiment to measure the relaxation rates associated with the $^4$I$_{11/2}$–$^4$I$_{15/2}$ transition of erbium embedded into congruent and stoichiometric lithium niobate single crystals. The erbium ions may occupy non-equivalent sites in the lithium niobate crystal by replacing the lithium ions, and simultaneously generating defects for charge compensation. We have done our measurements at two nearby frequencies which are the resonant transition frequencies of two non-equivalent erbium sites. First we have measured the spectral hole widths for the transition $^4$I$_{11/2}$–$^4$I$_{15/2}$, and using a simple theory, we have calculated the corresponding coherence relaxation time. We have obtained clearly distinguishable coherence times for the two different Er sites. Next, we have examined the dynamics of the population relaxation from the state $^4$I$_{11/2}$. We have found that the observed time dependence can be described by the sum of two exponential functions. The retrieved decay rates are close to earlier fluorescence spectroscopic measurements for the decay of the $^4$I$_{11/2}$ and that of the intermediate $^4$I$_{13/2}$ states. However, there is an order of magnitude difference between the theoretically predicted radiative and experimentally observed lifetimes for the $^4$I$_{11/2}$ level. The difference can be well described by a multiphonon relaxation process of the excited-state electrons in the rare earth ions. In our simple model calculation for the pump-probe experiment, based on a three level system furnished with dipole relaxation mechanism, the weights of the two exponential decay functions describing the total population relaxation process can be determined. This ratio can also be calculated from the actual measured decay time values, and the two ratios are different. Hence, this is also an indication that even though the simple three-state model seems to capture the essential physics, but it should be further elaborated to get better agreement between the measured and predicted lifetime values for the $^4$I$_{11/2}$ state. This was also the conclusion of earlier experimental works, where the decay process have been studied by time-resolved fluorescence.