1 Introduction

As is known from basic textbooks of optics, temporal coherence of a scalar beam of light leads to intensity fringes in Michelson’s interferometer when the path difference is varied [1, 2]. The temporal degree of coherence is directly given by the visibility of the intensity fringes and the coherence time can be deduced from the width of the fringe pattern. However, for a random, partially polarized light beam electromagnetic coherence does not appear only as intensity variation but also, or only, as polarization modulation [3]. Recently, this fact was used to relate spatial electromagnetic coherence to the modulation contrasts (visibilities) of the traditional spectral polarization (one-point) Stokes parameters in Young’s interferometer [4, 5]. For each parameter, the modulation contrast was shown to be given by the corresponding coherence (two-point) Stokes parameter [6] at the pinholes, establishing an illustrative connection between polarization and electromagnetic coherence.

In this Letter, we consider Michelson’s interferometer with partially polarized electromagnetic light and show that temporal coherence shows up at the output as time-domain intensity and polarization-state modulations. Specifically, we show that the temporal electromagnetic degree of coherence of a stationary, quasi-monochromatic beam is given by the visibilities of the Stokes-parameter variations on the observation screen. We also outline how the polarization modulations are transformed into intensity changes with quarter-wave plates in the arms, allowing one to measure the degree of coherence and the related coherence time. The theoretical formulation in this work is in terms of the classic polarization and temporal coherence (or two-time [7]) Stokes parameters, illuminating the interplay of polarization and electromagnetic coherence.

2 Michelson’s interferometer with electromagnetic light

A realization of a random, statistically stationary, uniformly partially polarized and partially temporally coherent electromagnetic beam, at time t, is given by column vector \({\mathbf {E}}(t) = [E_{x}(t), E_{y}(t)]^{\mathrm{T}}\), where T denotes the transpose. The wave field is taken to propagate along the z axis. The coherence properties of the field, at instants of time \(t_1\) and \(t_2\), are represented by the \(2\times 2\) mutual coherence matrix \(\varvec{{\varGamma }}(\tau ) = \langle {\mathbf {E}}^*(t){\mathbf {E}}^{\mathrm {T}}(t+\tau )\rangle\) [1, 8], where \(\tau = t_2-t_1\) and the angle brackets and asterisk denote ensemble average and complex conjugate, respectively. The temporal electromagnetic degree of coherence of the beam (in squared form) is given as [5, 9]

$$\begin{aligned} \gamma ^2(\tau ) = \frac{\mathrm{tr}\,\left[ \varvec{{\varGamma }}(\tau ) \varvec{{\varGamma }}(-\tau )\right] }{\mathrm {tr}^2[\varvec{{\varGamma }}(0)]}, \end{aligned}$$
(1)

where \({\mathrm {tr}}[\varvec{{\varGamma }}(0)]\) is the intensity of the field. The degree of coherence \(\gamma (\tau )\) is real and bounded within \(0\le \gamma (\tau )\le 1\), with the lower and upper limit corresponding to temporally incoherent and coherent fields, respectively.

Instead of describing temporal electromagnetic coherence using the mutual coherence matrix, one may employ an alternative but fully equivalent formulation in terms of the coherence (two-time) Stokes parameters defined as [5–7, 10]

$$\begin{aligned} {\mathcal {S}}_0(\tau )&= {\varGamma }_{xx}(\tau )+{\varGamma }_{yy}(\tau ),\end{aligned}$$
(2a)
$$\begin{aligned} {\mathcal {S}}_1(\tau )&= {\varGamma }_{xx}(\tau )-{\varGamma }_{yy}(\tau ),\end{aligned}$$
(2b)
$$\begin{aligned} {\mathcal {S}}_2(\tau )&= {\varGamma }_{xy}(\tau )+{\varGamma }_{yx}(\tau ),\end{aligned}$$
(2c)
$$\begin{aligned} {\mathcal {S}}_3(\tau )&= i\left[ {\varGamma }_{yx}(\tau )-{\varGamma }_{xy}(\tau )\right] , \end{aligned}$$
(2d)

where \({\varGamma }_{ij}(\tau ) = \langle E_i^*(t)E_j(t+\tau )\rangle\), \((i,j) \in (x,y)\), are the elements of \(\varvec{{\varGamma }}(\tau )\). Setting \(\tau = 0\), the coherence Stokes parameters reduce to the conventional (time-averaged) Stokes parameters as [1]

$$\begin{aligned} S_0&= J_{xx}+J_{yy},\end{aligned}$$
(3a)
$$\begin{aligned} S_1&= J_{xx}-J_{yy},\end{aligned}$$
(3b)
$$\begin{aligned} S_2&= J_{xy}+J_{yx},\end{aligned}$$
(3c)
$$\begin{aligned} S_3&= i\left[ J_{yx}-J_{xy}\right] , \end{aligned}$$
(3d)

where \(J_{ij} = {\varGamma }_{ij}(0)\), \((i,j) \in (x,y)\), are the elements of the polarization matrix \({\mathbf {J}}=\varvec{{\varGamma }}(0)\) describing the polarization properties of the field. The parameter \(S_0\) is the intensity, while \(S_1\), \(S_2\), and \(S_3\) characterize the (partial) polarization state, or more precisely, the state of polarization of the fully polarized part of the beam [11]. The use of coherence Stokes parameters makes the connection between electromagnetic coherence and polarization more transparent, as has been demonstrated in [4, 5, 12, 13].

By introducing the intensity-normalized coherence Stokes parameters via the formulas

$$\begin{aligned} \gamma _n(\tau ) = \frac{{\mathcal {S}}_n(\tau )}{S_0}, \qquad n \in (0,\ldots ,3), \end{aligned}$$
(4)

the electromagnetic degree of coherence of Eq. (1) can be shown to take on the form

$$\begin{aligned} \gamma ^2(\tau ) = \frac{1}{2}\sum _{n=0}^3\vert \gamma _n(\tau )\vert ^2. \end{aligned}$$
(5)

This expression follows on expanding \(\varvec{{\varGamma }}(\tau )\) in terms of the Pauli spin matrices [4, 7], or simply after some algebra using Eq. (2). We recall that the normalized (spectral) coherence Stokes parameters at the apertures of Young’s interferometer determine the modulation contrasts of the usual Stokes parameters on the observation screen [3]. The contrasts (or visibilities) of the intensity and polarization variations together specify the spatial electromagnetic degree of coherence, consistently with Eq. (5), and analogously to the traditional scalar result where, of course, only the intensity modulations occur [1, 14].

Fig. 1
figure 1

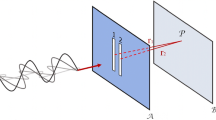
Illustration of Michelson’s interferometer. Input beam \({\mathbf {E}}^{({\mathrm {i}})}(t)\) is divided into two equal-intensity parts by beam splitter BS. The beams propagate distances \(L_1\) and \(L_2\) in the interferometer arms, reflect from mirrors M, and are recombined at BS to produce output beam \({\mathbf {E}}(t)\). The delay introduced by the length difference of the arms is \(\tau = 2(L_2-L_1)/c\), where c is the speed of light

Full size image

Let us now focus our attention on Michelson’s interferometer, as shown in Fig. 1. An electromagnetic beam \({\mathbf {E}}^{({\mathrm {i}})}(t)\) is incident on a 50:50 non-polarizing beam splitter, which divides the beam into two arms, where the beams propagate distances \(L_1\) and \(L_2\) to mirrors. The beams reflect and propagate back to the beam splitter, where they are recombined and the field at the output port is investigated. The optical path length in one of the arms can be varied by translating the mirror, resulting in a delay \(\tau = 2(L_2-L_1)/c\), with c being the speed of light. The output field is given as

$$\begin{aligned} {\mathbf {E}}(t)= \frac{1}{2}\left[ {\mathbf {E}}^{({\mathrm {i}})}(t)+{\mathbf {E}}^{({\mathrm {i}})}(t+\tau )\hbox {e}^{{\mathrm {i}}{\Delta }\phi }\right] , \end{aligned}$$
(6)

where the factor 1/2 originates from the fact that in two traversals across the beam splitter 1/4 of the energy is retained. The phase terms common to both fields are omitted. We have further denoted by \({\Delta }\phi\) the relative phase shift between the fields from the two arms, resulting from reflections and transmissions at the beam splitter.

After straightforward developments of Eqs. (2)–(6) the time-domain Stokes parameters at the output of the interferometer assume the forms

$$\begin{aligned} S_n(\tau ) = \frac{1}{2}S_n^{(\mathrm i)}+\frac{1}{2}S_0^{(\mathrm i)}\left| \gamma _n^{({\mathrm {i}})}(\tau )\right| \cos \{{\mathrm {arg}}[\gamma _n^{({\mathrm {i}})}(\tau )]+{\Delta }\phi \}, \end{aligned}$$
(7)

for all \(n \in (0,\ldots ,3)\). Above, the superscript \(({\mathrm {i}})\) refers to quantities associated with the incoming field and \({\mathrm {arg}}[b]\) is the phase of complex number b. Due to quasi-monochromaticity, \(\vert \gamma _n^{({\mathrm {i}})}(\tau )\vert\) is a slowly varying function of \(\tau\) (cf. [1]). Further, \({\mathrm {arg}}[\gamma _n^{({\mathrm {i}})}(\tau )]=\alpha _n(\tau )-\omega \tau\), where \(\omega\) is the center frequency and \(\alpha _n(\tau )\) likewise is slowly varying with \(\tau\). It follows that when the time delay is varied by translating the mirror in one of the arms, all Stokes parameters \(S_n(\tau )\) on the observation plane are sinusoidally modulated. The constant phase term \({\Delta }\phi\) affects the position of the variations.

Equation (7) can be regarded as the temporal interference law for the Stokes parameters. It demonstrates the fact that the relations among coherence and polarization can, in some cases, be made transparent in terms of the usual (polarization) Stokes parameters and the two-time (coherence) Stokes parameters. The visibilities of the modulations are given as

$$\begin{aligned} V_n(\tau ) = \frac{{\mathrm {max}}[S_n(\tau )]-{\mathrm {min}}[S_n(\tau )]}{{\mathrm {max}}[S_0(\tau )]+{\mathrm {min}}[S_0(\tau )]} = \left| \gamma _n^{({\mathrm i})}(\tau ) \right| , \end{aligned}$$
(8)

where max and min denote the maximum and minimum value in the neighborhood of delay \(\tau\), respectively. Hence, the visibilities of the Stokes-parameter modulations in a Michelson interferometer (equipped with a 50:50 non-polarizing beam splitter) are directly specified by the magnitudes of the normalized coherence Stokes parameters of the input field. Applying Eq. (8) to (5), the temporal electromagnetic degree of coherence of the input field is given as

$$\begin{aligned} \gamma ^{({\mathrm {i}})}(\tau ) = \left[ \frac{1}{2}\sum _{n=0}^3 V_n^2(\tau )\right] ^{1/2}. \end{aligned}$$
(9)

We therefore find that the visibilities of the time-domain intensity and polarization-state modulations in a Michelson interferometer characterize in a straightforward manner the temporal electromagnetic degree of coherence of a beam field. This result is a counterpart to that found earlier for spatial coherence in Young’s interferometer [4].

3 Detection of polarization modulations

According to Eq. (9), the temporal electromagnetic degree of coherence is obtained by recording the visibilities of the Stokes-parameter modulations. To this end, the polarization-state variations expressed by \(S_1(\tau )\), \(S_2(\tau )\), and \(S_3(\tau )\) are transferred into directly measurable intensity (\(S_0(\tau )\)) fringes. This is achieved by placing quarter-wave plates in the arms of the interferometer, as is shown in Fig. 2. We proceed to analyze the conversion of each polarization-state Stokes parameter separately.

Fig. 2
figure 2

Arrangements for transferring the polarization-state modulations into time-domain intensity variations. The Jones matrix \({\mathbf {Q}}(\theta )\) refers to a quarter-wave plate with \(\theta\) being the angle between the fast axis (f) and the x axis. a By inserting a quarter-wave plate with fast axis parallel to x axis in arm 2 and no elements in arm 1, the visibility of the intensity fringes gives \(V_1(\tau )\). b Polarization visibility \(V_2(\tau )\) is obtained from the intensity variations when the quarter-wave plate in arm 2 is rotated into angle \(\pi /4\). c Adding quarter-wave plates with fast axes parallel to x axis in both arms leads to the visibility of the intensity modulation giving \(V_3(\tau )\)

Full size image

It is convenient to express the effect of a quarter-wave plate in the Jones matrix formalism as [15]

$$\begin{aligned} {\mathbf {Q}}(\theta )&= \left( \begin{array}{cc} \cos ^2\theta -i\sin ^2\theta &\quad (1+i)\cos \theta \sin \theta \\ (1+i)\cos \theta \sin \theta &\quad \sin ^2\theta -i\cos ^2\theta \end{array} \right) , \end{aligned}$$
(10)

where \(\theta\) is the angle measured from the x axis to the fast axis of the wave plate. Note that the field propagates twice through the elements in the arms, first forwards and then, after mirror reflection, backwards. We present the field before and after the reflections (from mirrors and beam splitter) in a right-handed coordinate system [16]. Consequently, the Jones matrix of the wave plate in backward propagation is obtained by replacing \(\theta\) with \(-\theta\).

In order to transform the polarization modulations into the intensity variations, the required quarter-wave plates in the two arms are as follows. The visibility \(V_1(\tau )\) is accessed by inserting a quarter-wave plate with \(\theta =0\) into either arm, e.g., the arm with variable length (arm 2 in Fig. 2a). The fields from the two arms, denoted by \({\mathbf {E}}_1(t)\) and \({\mathbf {E}}_2(t)\) , respectively, are

$$\begin{aligned} {\mathbf {E}}_1(t)&= \frac{1}{\sqrt{2}} \hbox {e}^{i\phi _2}{\mathbf {C}}\frac{1}{\sqrt{2}}{\mathbf {C}}\hbox {e}^{i\phi _1}{\mathbf {E}}^{({\mathrm {i}})}(t) \nonumber \\&= \frac{1}{2}\hbox {e}^{i(\phi _1+\phi _2)}\left[ E_x^{({\mathrm {i}})}(t), E_y^{({\mathrm {i}})}\right] ^{\mathrm {T}},\end{aligned}$$
(11)
$$\begin{aligned} {\mathbf {E}}_2(t)&= \frac{1}{\sqrt{2}}{\mathbf {C}}\hbox {e}^{i\phi _4}{\mathbf {Q}}(0){\mathbf {C}}{\mathbf {Q}}(0)\frac{1}{\sqrt{2}}\hbox {e}^{i\phi _3}{\mathbf {E}}^{({\mathrm {i}})}(t+\tau )\nonumber \\&= \frac{1}{2}\hbox {e}^{i(\phi _3+\phi _4)}\left[ E_x^{({\mathrm {i}})}(t+\tau ),-E_y^{({\mathrm {i}})}(t+\tau )\right] ^{\mathrm {T}}, \end{aligned}$$
(12)

where \(\phi _j\), \(j \in (1,\ldots ,4)\), are the phase shifts in transmissions and reflections on the different sides of the beam splitter and \({\mathbf {C}} = {\mathrm {diag}}[-1,1]\) is a matrix that represents reflection from a mirror or the beam splitter; it takes into account the coordinate change and a \(\pi\) phase shift. The total field at the output of the interferometer is thus

$$\begin{aligned} {\mathbf {E}}(t) = \frac{1}{2}\left[ \left( \begin{array}{c} E_x^{({\mathrm {i}})}(t) \\ E_y^{({\mathrm {i}})}(t) \end{array} \right) + \left( \begin{array}{c} E_x^{({\mathrm {i}})}(t+\tau ) \\ -E_y^{({\mathrm {i}})}(t+\tau ) \end{array} \right) \hbox {e}^{i{\Delta }\phi }\right] , \end{aligned}$$
(13)

where \({\Delta }\phi = \phi _3+\phi _4-\phi _1-\phi _2\) and a constant phase term has been dropped. The related output intensity is given by

$$\begin{aligned} S_0(\tau ) = \frac{1}{2}S_0^{(\mathrm i)}+\frac{1}{2}S_0^{(\mathrm i)}\left| \gamma _1^{({\mathrm {i}})}(\tau )\right| \cos \{{\mathrm {arg}}[\gamma _1^{({\mathrm {i}})}(\tau )]+{\Delta }\phi \}. \end{aligned}$$
(14)

We see that \(V_1(\tau )\) related to the polarization modulations is obtained from the visibility of the intensity fringes by inserting a quarter-wave plate into one of the arms.

By rotating the quarter-wave plate in arm 2 by \(\theta =\pi /4\) and keeping arm 1 empty (see Fig. 2b), we find

$$\begin{aligned} {\mathbf {E}}_2(t)&= \frac{1}{\sqrt{2}}{\mathbf {C}} \hbox {e}^{i\phi _4}{\mathbf {Q}}(-\pi /4){\mathbf {C}}{\mathbf {Q}}(\pi /4)\frac{1}{\sqrt{2}}\hbox {e}^{i\phi _3}{\mathbf {E}}^{({\mathrm {i}})}(t)\nonumber \\&= \frac{1}{2}\hbox {e}^{i(\phi _3+\phi _4)}\left[ E_y^{({\mathrm {i}})}(t), E_x^{({\mathrm {i}})}(t)\right] ^{\mathrm {T}}, \end{aligned}$$
(15)

while \({\mathbf {E}}_1(t)\) is as in Eq. (11). The total output field becomes

$$\begin{aligned} {\mathbf {E}}(t) = \frac{1}{2}\left[ \left( \begin{array}{c} E_x^{({\mathrm {i}})}(t) \\ E_y^{({\mathrm {i}})}(t) \end{array} \right) + \left( \begin{array}{c} E_y^{({\mathrm {i}})}(t+\tau ) \\ E_x^{({\mathrm {i}})}(t+\tau ) \end{array} \right) \hbox {e}^{i{\Delta }\phi }\right] , \end{aligned}$$
(16)

and, in analogy to Eq. (14), the visibility of the intensity fringes now gives \(V_2(\tau )\) of the polarization modulations.

Finally, keeping the quarter-wave plate with \(\theta =\pi /4\) in arm 2 but adding into both arms quarter-wave plates with \(\theta =0\) (as in Fig. 2c) results in

$$\begin{aligned} {\mathbf {E}}_1(t)&= \frac{1}{\sqrt{2}} \hbox {e}^{i\phi _2}{\mathbf {Q}}(0){\mathbf {C}}{\mathbf {Q}}(0)\frac{1}{\sqrt{2}}{\mathbf {C}}\hbox {e}^{i\phi _1}{\mathbf {E}}^{({\mathrm {i}})}(t)\nonumber \\&= \frac{1}{2}\hbox {e}^{i(\phi _1+\phi _2)}\left[ E_x^{({\mathrm {i}})}(t), -E_y^{({\mathrm {i}})}(t)\right] ^{\mathrm {T}}, \end{aligned}$$
(17)
$$\begin{aligned} {\mathbf {E}}_2(t)&= \frac{1}{\sqrt{2}}{\mathbf {C}} \hbox {e}^{i\phi _4}{\mathbf {Q}}(0){\mathbf {Q}}\left( -\pi /4\right) {\mathbf {C}}\nonumber \\&\quad\times {\mathbf {Q}}\left( \pi /4\right) {\mathbf {Q}}(0)\frac{1}{\sqrt{2}}\hbox {e}^{i\phi _3}{\mathbf {E}}^{({\mathrm {i}})}(t+\tau )\nonumber \\&= -\frac{i}{2}\hbox {e}^{i(\phi _3+\phi _4)}\left[ E_y^{({\mathrm {i}})}(t+\tau ),E_x^{({\mathrm {i}})}(t+\tau )\right] ^{\mathrm {T}}. \end{aligned}$$
(18)

The total field then is

$$\begin{aligned} {\mathbf {E}}(t) = \frac{1}{2}\left[ \left( \begin{array}{c} E_x^{({\mathrm {i}})}(t) \\ -E_y^{({\mathrm {i}})}(t) \end{array} \right) -i \left( \begin{array}{c} E_y^{({\mathrm {i}})}(t+\tau ) \\ E_x^{({\mathrm {i}})}(t+\tau ) \end{array} \right) \hbox {e}^{i{\Delta }\phi }\right] , \end{aligned}$$
(19)

and, as above, the related intensity-fringe visibility is found to be \(V_3(\tau )\). From the measured values of \(V_n(\tau )\), \(n \in (0,\ldots ,3)\), the temporal electromagnetic degree of coherence \(\gamma ^{(i)}(\tau )\) of the input beam is obtained as shown by Eq. (9).

4 Summary and conclusions

In summary, we have demonstrated that the temporal electromagnetic coherence can appear as time-domain intensity or polarization-state modulation, or both. More specifically, for a stationary, quasi-monochromatic, uniformly partially polarized and temporally partially coherent beam of light, the electromagnetic degree of coherence in the time domain is given by the visibilities of the variations of the Stokes parameters in Michelson’s interferometer and it can straightforwardly be measured through the use of standard wave plates. This result opens up a way to evaluate the coherence time of a random, partially polarized light beam. In general, our work provides further physical evidence of the fact that the relationship between polarization and electromagnetic coherence can be quite transparent when assessed in terms of the conventional Stokes parameters and the newer coherence (two-point or two-time) Stokes parameters.