Free charge carrier absorption in silicon at 800 nm

Abstract

The transmission of a Ti:sapphire laser beam (c.w. and fs pulsed operation at 800 nm) through a 10-μm-thin oxidized silicon membrane at 45° angle of incidence at first increases with the incident laser power, then shows a maximum, and finally decreases considerably. This nonlinear transmission behavior is the same for c.w. and pulsed laser operation and mainly attributed to free charge carrier absorption (FCA) in Si. A simple FCA model is developed and tested.

1 Introduction

Today silicon (Si) continues to be a prominent material in microelectronics, optoelectronics, micromechanics, solar cells, and increasingly in photonics. To prepare, modify, and/or shape Si material and delicate Si devices, a broad spectrum of techniques has been established. In particular, laser technology provides a manifold of remote, contactless, spatially confined and time-controlled methods for, e.g., doping, annealing, crystallization, and ablation. These require, however, a proper control and understanding of the linear and nonlinear optical properties of Si. Typically, laser light shows a narrow spectral bandwidth, high intensity as well as spatial and temporal confinement. Therefore, particularly the nonlinear optical properties of Si are of utmost importance including their laser-induced changes by heating and/or electronic excitation.

Some of the nonlinear optical properties of Si may occur simultaneously and be difficult to discriminate like coherent two-photon absorption (TPA), free carrier absorption (FCA), and thermally induced absorption enhancement (TAE) [1]. Moison et al. argue that TAE is dominant over FCA for probe photon energies $h\nu \ge 2$ eV, whereas FCA dominates for $h\nu < 2$ eV. Coherent TPA, on the other hand, is unlikely for photon energies below half of the bandgap for the direct optical interband transition, i.e., $h\nu <1.7$ eV ($\lambda >730$ nm). This statement is important because many laser experiments with Si nowadays are performed with Ti:sapphire femtosecond (fs) lasers operating in this wavelength range at high intensity. The above findings were, however, obtained at a low laser pulse repetition rate of 20 Hz only [1], whereas fs lasers typically provide repetition rates of 1 kHz with amplifiers or even 80 MHz in the oscillator mode.

The lifetime of thermalized electrons in the conduction band (CB) of Si or, equivalently, of thermalized electron–hole (eh) pairs ranges around $\tau _\mathrm{eh}\approx 10\,\upmu{\hbox{s}}$ for intrinsic and weakly doped Si samples [2–4]. This relatively long lifetime reflects the indirect character of the optical interband transition in Si and is much longer than the typical duration of ultrashort (fs to ps) or even short (ns to μs) laser pulses. Therefore, eh pairs can accumulate in Si during long laser pulses and/or during a pulse train of about 100 kHz or higher repetition rate. This leads to increasingly strong absorption of the laser beam by free charge carriers in two ways: (1) FCA is possible within the same laser pulse (a) by “hot” charge carriers (directly after generation) and (b) by “cold” carriers in relatively long laser pulses (“cooling” within about 100 fs [6]). (2) FCA by “cold” carriers occurs in the subsequent laser pulse if its delay is shorter than the eh pair lifetime.

FCA has a long history of more than half a century (cf., e.g., [5]) and was at first investigated by standard spectroscopy and conventional free charge carrier generation. With the advent of lasers, however, the contactless and well-confined photogeneration of free carriers has become amenable, convenient, and increasingly important in both laser processing and diagnostics.

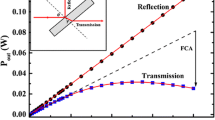
In this paper, the same Ti:sapphire laser is applied in both operational modes continuous wave (c.w.) and fs pulse trains, to investigate the nonlinear optical behavior of the same 10-μm-thin Si sample by measuring the average laser power reflected from and transmitted through this membrane as a function of the incident laser power (Fig. 1). The main experimental findings, independently obtained in two laboratories under slightly different conditions, are essentially identical for c.w. and pulsed operation at 800 nm (1.55 eV). They are discussed in terms of FCA and compared to previous findings in the literature.

2 Experiments

For the transmission measurements, two similar experimental setups at two institutes, the IPHT (Leibniz Institute of Photonic Technology) and the LRI (Laser Research Institute), are used. Both setups feature a Ti:sapphire laser beam ($\lambda \approx 800$ nm) to irradiate the Si sample at an external angle of incidence $\theta = 45{^{\circ }}$ (Fig. 1). Commercial oscillators (IPHT: Coherent Mira 900F, LRI: Spectra Physics, 3941-M3S, Tsunami) provide average powers up to 1 W at 76 and 80 MHz repetition rate, respectively. The pulse durations of 130 (IPHT) and 75 fs (LRI) are determined by APE Pulse Scope autocorrelator (IPHT) or a custom-built autocorrelator (LRI). At both research facilities, pulsed and c.w. laser irradiation is applied. The beam polarization (p-polarization) is defined by polarizing beam splitters (PBS) combined with two half-wave plates for power adjustment and polarization control.

Fig. 1

Scheme of the experiments to compare laser beam reflection from and transmission through thin silicon membranes; external angle of incidence $\theta =45{^\circ }$; propagation angle within silicon $\gamma \approx 11 {^{\circ }}$

At the IPHT, the 130 fs pulses are prolonged to about 138 ± 4 fs by the calcite PBS as confirmed by the autocorrelation measurements. The incident laser light is focused onto the sample surface by a combination of $f_1 = -50$ mm and $f_2 = 35$ mm lenses to a focal spot diameter of 13 ± 2 μm. The focal plane position is controlled by a z-scan-like measurement. The transmitted light is collimated by a $f_3 = 100$ mm lens. Two identical photomultiplier tubes (PMT, Hamamatsu H10720P-110) with neutral density filters (OD > 4) are connected to two identical photon counters (SRS, SR430) for simultaneous signal recording in transmission and reflection directions. Furthermore, simple air flushing is optionally applied for sample cooling.

At the LRI, the 75 ± 5 fs laser pulses are prolonged to about 90 fs by the optical components including the PBS. The beam is collimated, focused by two lenses ($f_4 = -50$ mm and $f_5 = 35$ mm) to a focal diameter of 13 ± 2 μm. The transmitted light is collected by a lens with $f_6 = 125$ mm. Power meters are used to measure the transmitted and reflected average powers.

The samples are prepared from commercial $\left\langle 100\right\rangle$-Si wafers by chemical etching using tetramethylammonium hydroxide (TMAH) to produce thin membranes of $3\times 3\hbox { mm}^{\text {2}}$ area and a thickness of $z_\mathrm{m} \approx 10\,\upmu$m. The wafers are slightly p-doped (3…6 × 10¹⁴ cm⁻³). Prior to investigations, the membranes are cleaned by using acetone and hydrofluoric acid to remove dirt and old oxide layers, respectively. In contact with air, the clean surfaces oxidize under dark room conditions reaching an equilibrium thickness of 2.5 ± 0.5 nm within 48 h (cf., e.g., [7]).

3 Results and discussion

Continuous wave and pulsed laser radiation ($\lambda = 800$ nm) were applied at 45° external angle of incidence onto thin, naturally oxidized Si membranes of about 10 μm thickness. Figure 2 shows the results of laser beam reflection from (part A) and transmission through the membrane (part B) as a function of the incident average laser power $P_\mathrm{in}$ up to about 0.8 W on the sample, equivalent to average intensities of up to $4.3\times 10^5\,{\text {W/cm}^2}$ (IPHT and LRI). It is pointed out that the same transmission values are measured for rising or decreasing laser power $P_\mathrm{in}$ (i.e., no hysteresis).

Fig. 2

Average laser power reflected from (a) and transmitted through (b) a 10-μm-thin Si membrane as a function of the incident average laser power measured at IPHT and LRI in c.w. and fs laser pulsed operation at 800 nm with and without air flushing of the sample (cf. text)

Laser beam reflection $P_\mathrm{re}$ displays a nearly perfect linear dependence on the incident laser power $P_\mathrm{in}$ (part A, Fig. 2). This finding is in agreement with previous reports (cf., e.g., [8]) and confirms the validity of the Fresnel equations using the optical constants of the sample under ambient conditions. The transmitted laser power $P_\mathrm{tr}$ deviates, however, considerably from linearity (part B, Fig. 2) for both pulsed and c.w. laser irradiation: Starting with an initial linear increase of $P_\mathrm{tr}$ for low power $P_\mathrm{in}<0.3$ W, the transmission reaches a maximum value at $P_\mathrm{in}\approx 0.5$ W for c.w. and at 0.6 W for pulsed irradiation. For higher laser power $P_\mathrm{in}$, the transmission signal $P_\mathrm{tr}$ decreases again. This behavior is slightly affected by air flushing of the sample, yielding higher $P_\mathrm{tr}$ values (Fig. 2, part B). Contributions from internally reflected beams to the transmitted laser power $P_\mathrm{tr}$ are negligible ($\le$ about 2 %) because of the high reflection losses at the interfaces, even without any account for laser beam attenuation by absorption and/or scattering. The average pulse peak intensities on the sample amount to 41 (IPHT) and 59 GW/cm$^2$ (LRI) averaged over the beam cross section and the pulse duration.

Following the essence of many articles on laser interactions with Si, the discussion at first is focused on FCA as the dominant effect controlling the above experimental findings (cf., e.g., [1, 4, 6, 8–21]). Afterward, possible contributions from coherent TPA and/or multi-photon excitation will be discussed which, however, can result in a saturation of the laser beam transmission only, but not in its observed decrease with increasing incident power (part B, Fig. 2). Furthermore, laser-induced sample heating will be considered as well to obtain a consistent picture of the new results.

Laser-induced FCA has been investigated in many laboratories under very different conditions (cf., e.g., [1, 8, 15, 18–26]). It typically depends on the sample thickness and irradiation details like the wavelength, c.w. or pulsed laser operation, pulse repetition rate, temporal and spatial pulse shapes. Furthermore, the detection method of the transmitted light is of importance like time or individual pulse-resolved detection or pulse train-averaged records. As a result, different functionalities between the incident and the transmitted laser light are observed and in many cases prohibit their direct comparison as is easily verified if looking at the many different ways of data presentation in the literature.

Looking at the related literature, such a transmission behavior, i.e., with a maximum in the transmitted power (intensity, fluence) followed by a pronounced decrease, was implicitly reported by Yamada et al. [15] for the irradiation of a 0.6-μm-thin Si layer on sapphire by $\tau _p=250$ ns dye laser pulses at 590 nm: After transformation of their experimental transmission coefficients (Fig. 3 in [15]) to the transmitted intensity $I_\mathrm{tr}$ (Fig. 3), a maximum of $I_\mathrm{tr}=3$ a.u. is observed at the incidence fluence $\varPhi _\mathrm{in}\approx 0.35 {\hbox {J/cm}^{2}}$ and a steep decrease of $I_\mathrm{tr}$ toward higher incident fluences. For large $\varPhi _\mathrm{in}$ values, a constant transmission level of $I_\mathrm{tr}\approx 1.5$ a.u. is observed (Fig. 3).

It is challenging to find suitable fitting curves for the laser transmission data in part B of Fig. 2 and in Fig. 3 and to rationalize these findings. To begin with, it is assumed that the effective absorption coefficient of the sample $\alpha _\mathrm{eff} = \alpha _1 + \alpha _\mathrm{FCA}$ is composed of $\alpha _1$, the linear, small signal absorption coefficient of unperturbed Si and the FCA contribution $\alpha _\mathrm{FCA}$. Usually, the FCA coefficient $\alpha _\mathrm{FCA}$ is set proportional to the absorption cross section $\sigma _\mathrm{eh}$ and the density of eh pairs $n_\mathrm{eh}=n_\mathrm{e}=n_\mathrm{h}$ upon photogeneration: $\alpha _\mathrm{FCA}=n_\mathrm{eh}\cdot \sigma _\mathrm{eh}$ (cf., e.g., [1, 18, 20]). The eh pair distribution along the optical pathway in Si is here assumed to be approximately homogeneous because charge carrier diffusion is relatively fast in Si [1] and a stationary $n_\mathrm{eh}$ value builds up during the measurement time. The measured transmitted laser power then is in both cases, c.w. or pulsed laser operation, related to the homogeneous stationary $n_\mathrm{eh}$ concentration and therefore a z-independent constant $\alpha _\mathrm{FCA}$ value. Both depend, however, on $I_0$ i.e., $n_\mathrm{eh}=n_\mathrm{eh}\left( I_0\right)$ and $\alpha _\mathrm{FCA}=\alpha _\mathrm{FCA}\left( I_0\right)$, with $I_0$ being the intensity directly behind the entrance Si/SiO$_{\text {2}}$ interface. In addition, $\sigma _\mathrm{eh}$ depends on $n_\mathrm{eh}$ [6, 10], i.e., $\sigma _\mathrm{eh}=\sigma _\mathrm{eh}\left( n_\mathrm{eh}\left( I_0\right) \right)$. As a result, the relation between the intensities $I\left( z_\mathrm{m}\right)$ directly in front of the exit Si/SiO$_{2}$ interface and a given $I_0$ value follows the relation

$$\begin{aligned} I\left( I_0,z_\mathrm{m}\right)&=I_0\cdot \exp \left( -\alpha _\mathrm{eff}z_\mathrm{m}\right) \\ \nonumber&=I_0\cdot \exp \left( -\alpha _1 z_\mathrm{m}\right) \cdot \exp \left( -n_\mathrm{eh}\sigma _\mathrm{eh} z_\mathrm{m}\right) . \end{aligned}$$

(1)

The geometric laser path length through the Si membrane $z_\mathrm{m}$ is given by $z_\mathrm{m}=d_\mathrm{Si}/\cos \gamma$. For fixed $z_\mathrm{m}$, the calculated and measured intensities at $z=z_\mathrm{m}$ depend on $I_0$, $n_\mathrm{eh}$ and $\sigma _\mathrm{eh}$ while $z_\mathrm{m}$, $\alpha _1$ are constant values. The $n_\mathrm{eh}$ value is dominated by the optical generation of free carriers, their ambipolar diffusion within and out of the probed volume, and eh pair recombination [1]. The increase of $\sigma _\mathrm{eh}$ with $n_\mathrm{eh}$ is due to increasing carrier–carrier scattering taking place at $n_\mathrm{eh}>2\times 10^{17}{\hbox {cm}^{-3}}$ [6]. As a first approach, $\alpha _\mathrm{FCA}=n_\mathrm{eh}\sigma _\mathrm{eh}\left( n_\mathrm{eh}\right) =\kappa _n I_0^n$ is selected with $n=1$ or 2, implemented into Eq. 1 and tested in Fig. 3 using the transformed data of Yamada et al. [15] (cf. curves i and ii). Obviously, curves i (for $n=1$) and ii (for $n=2$) fail to reproduce the steep $I_\mathrm{tr}$ increase, the position of the $I_\mathrm{tr}$ maximum and the steep $I_\mathrm{tr}$ decrease to the plateau of nearly constant $I_\mathrm{tr}$ values for large $\varPhi _\mathrm{in}$ values. This failure is reflected by the small correlation coefficient below 0.5 for curves i and ii. It turns out necessary and sufficient, however, to introduce into Eq. 1 a further parameter $I_\mathrm{c}$ (cf. Eq. 2). For $I_0\ge I_\mathrm{c}$:

$$\begin{aligned} \nonumber I(I_0)&=\left( I_0-I_\mathrm{c}\right) F\cdot \exp \left( -E_n I^n_0\right) +F I_\mathrm{c}\\ \nonumber&= I_0 F\cdot \exp \left( -E_n I^n_0\right) - I_\mathrm{c} F\cdot \exp \left( -E_n I^n_0\right) +F I_\mathrm{c} \\&= I_0 F\cdot \exp \left( -E_n I^n_0\right) + I_\mathrm{c} F\cdot \left[ 1-\exp \left( -E_n I^n_0\right) \right] \end{aligned}$$

(2)

In Eq. 2, the abbreviations $F=\exp \left( -\alpha _1 z_\mathrm{m}\right)$ and $E_n=\kappa _n z_\mathrm{m}$ with $n=1$ or 2 are used. For $I_0<I_\mathrm{c}$, this Eq. 2, however, gives the physically unreasonable result that $I\left( I_0\right) >I_0\exp \left( -\alpha _1 z_\mathrm{m}\right)$, i.e., laser beam transmission larger than that expected from one-photon absorption. As too little data are available in this small range to determine the behavior accurately, we define for $I_0<I_\mathrm{c}$:

$$\begin{aligned} I\left( I_0\right) =I_0 F=I_0\cdot \exp {\left( -\alpha _1 z_\mathrm{m}\right) }. \end{aligned}$$

(3)

The resultant fit curves iii (for $n=1$) and iv (for $n=2$) nicely match the experimental findings as confirmed by their large correlation coefficients of 0.91 and 0.99, respectively. The preferred fit curve iv is based on the parameters $F=0.74$ for $\alpha _1=5000{\hbox { cm}^{-1}}$ [27, 28] and $z_\mathrm{m}=0.6\,\upmu$m [15], $I_\mathrm{c}=0.14{\hbox { J/cm}^2}$ together with the scaling factors $I_0/\varPhi _\mathrm{in}=0.80$ and $I\left( I_0,z_\mathrm{m}\right) /I_\mathrm{tr}\approx 0.05{\hbox {J/cm}^2}$ for the abscissa and ordinate scales in Fig. 3, respectively. The $I_0/\varPhi _\mathrm{in}$ value describes the laser beam attenuation ($\lambda =590$ nm) by Fresnel reflection at the air/sapphire and sapphire/silicon interfaces upon entering the Si sample.¹ The $I\left( I_0,z_\mathrm{m}\right) /I_\mathrm{tr}$ value implies that, for example, the maximum $\hbox {I}_{\mathrm{tr}}{[\hbox {a.u.}]}$ value corresponds to $I\left( I_0,z_\mathrm{m}\right) \approx 0.15$ J/cm$^2$, i.e., the laser beam value before leaving the Si sample through the Si/SiO₂ and SiO$_2$/air interfaces at the rear side (see footnote 1). The obtained parameter $I_\mathrm{c}$ can be understood as a constant amount of incident laser energy per pulse which contributes to the linear absorption ($\alpha _1$) but not to FCA. Such a behavior is expected if, for example, part of the generated eh pairs are out of resonance with the incident laser beam.

Fig. 3

Experimental transmission values $I_\mathrm{tr}$ from Yamada et al. [15] as a function of the incident laser pulse fluence $\varPhi _\mathrm{in}$ (590 nm, 250 ns) with the value pair ($\varPhi _\mathrm{in}=0$, $I_\mathrm{tr}=0$) added. The fitting curves i to iv are explained in the text

It appears attractive to compare the results by Yamada et al. (Fig. 3) to the data obtained at IPHT and LRI using Ti:sapphire lasers ($\lambda =800{\hbox { nm}}$) and 10-μm-thick Si membranes (Fig. 2, part B). Common features of both experimental series are their pronounced maxima of the transmitted power (pulse energy fluence) upon increasing the average incident power (fluence). The available and applied Ti:sapphire laser power seems to be insufficient to achieve a constant transmitted power in Fig. 2 B (plateau formation) in analogy to the finding in Fig. 3.

It is instructive to plot the experimental data of Fig. 2, part B in a different form by calculating the difference

$$\begin{aligned} \Delta I(I_0)=I^0(I_0)-I(I_0) \end{aligned}$$

(4)

with $I^0(I_0) \equiv I_0\cdot \exp \left( -\alpha _1 z_\mathrm{m}\right)$. $\Delta I(I_0)$ describes the FCA-related deviation from pure one-photon absorption and is calculated by subtracting the measured transmitted intensity $I_\mathrm{tr}\left( I_0\right)$ from the value $I^0\left( I_0\right)$ calculated using $\alpha _1=604\,{\hbox {cm}^{-1}}$ [29] and $z_\mathrm{m}=10{\upmu\hbox{m}}$. Plotting $\sqrt{\Delta I\left( I_0\right) }$ shows an approximately linear relation between $\sqrt{\Delta I\left( I_0\right) }$ and $P_\mathrm{in}\sim I_0$ in the investigated power range (Fig. 4). For all four data sets, the trend line intersects the abscissa at a value $P_\mathrm{in}>0$, indicating a threshold for the development of $\Delta I\left( I_0\right) \ge 0$ with the $P_\mathrm{in}$ threshold being related to the $I_\mathrm{c}$ term in Eq. 2. The small values $\sqrt{\Delta I\left( I_0\right) }$ measured below the threshold $P_\mathrm{in}$ value (Fig. 4) may be due to other contributing mechanisms (cf. below) as zero values are expected when Eq. 3 is considered for $I_0<I_\mathrm{c}$. The threshold in this model ($I_\mathrm{c}$ in Eq. 2) represents a constant part of $P_\mathrm{in}$ contributing to linear absorption only, but not to FCA (cf. above).

Fig. 4

The square root $(\Delta I)^{0.5}$ of the difference $\Delta I(I_0) = I^0(I_0) - I(I_0) \sim P_\mathrm{tr}^{calc}(P_\mathrm{in}) - P_\mathrm{tr}^{meas}(P_\mathrm{in})$ representing the FCA contribution as a function of the incident laser power $P_\mathrm{in}$ (cf. text)

The approximately linear plots $\sqrt{\Delta I\left( I_0\right) }$ versus $P_\mathrm{in}$ in Fig. 4 confirm that $\alpha _\mathrm{FCA}\sim I_0^n$ with $n=2$. Any other value of n results in significant deviations from linearity. The dependence of $\alpha _\mathrm{FCA}=n_\mathrm{eh}\sigma _\mathrm{eh}\left( n_\mathrm{eh}\right)$ on $I_0^2$ can be rationalized by using the recent paper of Meitzner et al. [6]: The dependence of $\sigma _\mathrm{eh}$ (called $\sigma _\mathrm{FCA}$ in [6]) on the free carrier concentration $n_\mathrm{eh}$ is graphed in Fig. 4 of [6]. Redrawing this graph with a linear abscissa scale $n_\mathrm{eh}\le 3\times 10^{20}{\hbox {cm}^{-3}}$ reveals to a first approximation that $\sigma _\mathrm{eh}\sim n_\mathrm{eh}$ or $\sigma _\mathrm{eh}=\sigma _0 n_\mathrm{eh}$ with the proportionality constant $\sigma _0$ yielding $\alpha _\mathrm{FCA}=n_\mathrm{eh}\sigma _\mathrm{eh}\left( n_\mathrm{eh}\right) =\sigma _0 n_\mathrm{eh}^2$. Assuming furthermore $n_\mathrm{eh}\sim P_\mathrm{in}$ or $I_0$, because eh pairs are generated by linear one-photon absorption, then $n_\mathrm{eh}=\kappa I_0$. This yields $\alpha _\mathrm{FCA}=\sigma _0 n_\mathrm{eh}^2 = \sigma _0\kappa ^2 I_0^2=\kappa _2 I_0^2$ as observed in both our results and those of Yamada et al. [15].

It is pointed out that the FCA contribution is based on two sequential one-photon absorption processes and essentially different from coherent two-photon absorption. In FCA, the first photon serves to generate an eh pair (interband transition) which in the second step undergoes a one-photon intraband excitation within the conduction band (electron) or the valence band (hole). The accumulation of an equilibrium density of eh pairs during pulsed or c.w. laser irradiation decouples the rate equations of the first and the second steps in FCA. The absence (or minor influence) of coherent 2- or multiphoton absorption is immediately evident from the very similar results obtained with c.w. and fs pulsed laser irradiation (Figs. 2, 4).

The effect of laser-induced sample heating can be fairly high as, for example, in case of 0.5-μm-thin Si layers on sapphire yielding $\Delta T\le 900\,{\text {K}}$ [26] or very small for Si wafers yielding $\Delta T\le 10\,{\text {K}}$ [30]. In our intermediate case of 10-μm-thin Si wafers, the laser-induced temperature rise was observed by an IR camera to be $\Delta T \approx 10\,{\text {K}}$. Application of the known temperature dependence $\alpha (T,800{\text {nm}})$ of the Si small signal absorption coefficient [28, 31] shows that this temperature rise reduces the laser beam transmission by about 1 % only (9 % in case of $\Delta T=100\,{\text {K}})$. Purging of the Si sample with ambient air increased the c.w. laser beam transmission by about 15 % or less (Fig. 2). The relation between the FCA contribution $\Delta I(I_0)$ and the incident laser power $P_\mathrm{in}$ (slope $d\Delta I(I_0)^{0.5}/dP_\mathrm{in})$, on the other hand, remains unaffected (Fig. 4).

The correlation between the fit parameters in Fig. 2b and the measurement values is established by the use of $\alpha _1=604 {\hbox {cm}^{-1}}$, $z_\mathrm{m}=10{\upmu \hbox {m}}$, and $I_0=0.845\cdot P_\mathrm{in}$ [Fresnel reflection at the air/SiO₂ and Si/SiO₂ interfaces (see footnote 1)]. Values of $0.15 {\hbox {W}\le I_\mathrm{c}\le 0.2{\hbox {W}}}$ are found for the c.w. and $0.24{\hbox {W}}\le I_\mathrm{c}\le 0.24{\hbox {W}}$ for the fs laser experiments in agreement with the plots in Fig. 4. Equation (2) and the above relation $\alpha _\mathrm{FCA}=\sigma _0 n_\mathrm{eh}^2=\kappa _2 I_0^2$ are used to estimate the stationary concentration of free charge carriers by $n_\mathrm{eh}=I_0\cdot \sqrt{E_2/\left( \sigma _0 z_\mathrm{m}\right) }$. The unknown value $\sigma _0$ is derived from ref. [20], for $\lambda =800{\hbox { nm}}$ (IPHT & LRI) and $\lambda =590{\hbox { nm}}$ (Yamada et al. [15]) in different ways. For $\lambda =800 {\hbox { nm}}$, the value $\sigma _\mathrm{eh}=\sigma _0 n_\mathrm{eh}\approx 10^{17}{\hbox { cm}^2}$ with $n_\mathrm{eh}=1.4\times 10^{18}{\hbox { cm}^{-3}}$ is derived from Figs. 2(c), 3(a) and 3(b) of Ref. [20]. This value $\sigma _\mathrm{eh}$ is roughly estimated to lie between the $\sigma _\mathrm{eh}$ values of nanocrystalline and bulk Si and leads to $\sigma _0\left( 800 {\hbox { nm}}\right) \approx 5\times 10^{-36}{\hbox { cm}^5}$ resulting in $1.7\times 10^{18}{\hbox { cm}^{-3}}\le n_\mathrm{eh}\left( I_0=0.1\hbox { W}\right) \le 2.1\times 10^{18}{\hbox { cm}^{-3}}$ and $1.5\times 10^{19}{\hbox { cm}^{-3}}\le n_\mathrm{eh}\left( I_0=0.9\hbox { W}\right) \le 2.0\times 10^{19}{\hbox { cm}^{-3}}$. These values are placed well below the Si damage threshold.

The value $\sigma _0\left( \lambda =590\hbox { nm}\right) \approx 1.2\times 10^{-39}{\hbox { cm}^5}$, on the other hand, is extrapolated using the relation $\sigma _\mathrm{FCA}(\lambda )=(5\pm 2)\times 10^{-9}\lambda ^{2.0\pm 0.3}{\hbox { cm}^2}$ [20] ($\sigma _\mathrm{FCA}(\lambda )$ corresponds to $\sigma _\mathrm{eh}(\lambda )$ in this paper). Using this value $\sigma _0(\lambda =590\hbox { nm})$, eh pair concentrations $7\times 10^{20}{\hbox { cm}^{-3}}\le n_\mathrm{eh}\le 2\times 10^{22}{\hbox { cm}^{-3}}$ at $I_0=0.1\,{\hbox{J\,cm}^{-2}}$ and $2.5\,{\hbox{J\,cm}^{-2}}$ are obtained, respectively. The high $n_\mathrm{eh}$ value at $2.5\,{\hbox {J\,cm}^{-2}}$ is in agreement with the reported laser damage of the sample.

To conclude, the applied approximations and fit procedures appear applicable. The fit curves in Fig. 2, part B and Fig. 3 were obtained using Eq. 2 and $n=2$. In case of the LRI data, a small abscissa scale offset of 0.025 W turned out helpful. Overall, the obtained results can be fitted and rationalized within a simple model of FCA. This finding is encouraging particularly as both laser wavelengths might generate a complex situation: FCA at these wavelengths can compete with the indirect optical transition of Si, i.e., the generation of eh pairs. The empirically found power law following the square of the incident average laser power (or pulse energy fluence) can be rationalized by a linear dependence of the eh pair absorption cross section $\sigma _\mathrm{eh}=\sigma _0 n_\mathrm{eh}$ on the density of eh pairs in the investigated $n_\mathrm{eh}$ region and by assuming a linear relation between the incident laser power and the stationary concentration $n_\mathrm{eh}$ of free carriers. Thus, a simple and consistent picture has been established. We expect an $I(I_0)$ plateau—like that in Fig. 3—corresponding to 40 ± 10 % of the maximum $I(I_0)$ values in part B of Fig. 2 in the so far experimentally non-accessible region $P_\mathrm{in}>1\hbox { W}$.

4 Summary and conclusion

In summary, the above results appear to pave the way for further well-designed experimental and theoretical investigations of the complex interactions between Ti:sapphire lasers and thin crystalline silicon samples. This combination of a technologically relevant and flexible laser system and a prominent semiconductor appears very promising in particular for sample thicknesses $z_\mathrm{m}\approx l_\mathrm{abs}(\lambda _L)$ lying in the range of the relevant absorption length $l_\mathrm{abs}(\lambda _L)$.

The absorption of Ti:sapphire laser light by slightly p-doped silicon was investigated under c.w. and fs pulsed laser operation using a 10-μm-thin membrane. The average laser power incident onto the sample was increased up to about 1 W. This variation revealed a strong nonlinear power (intensity) dependence of the beam transmission through the sample, whereas laser beam reflection remained a linear function. The nonlinearity observed with the laser beam transmission is essentially the same for c.w. and pulsed laser irradiation and mainly attributed to free carrier absorption (FCA) in silicon. Laser-induced sample heating and coherent two- and/or multi-photon absorption were shown to be of minor importance only.

Similar results previously obtained by using a pulsed dye laser at 590 nm irradiating a 0.6-μm-thick Si layer on sapphire [15] show a pronounced maximum followed by a lower constant transmission for further increasing input intensity (Fig. 3). This complex transmission behavior could nicely be fitted by a simple FCA model.

The FCA model has been applied to the only laser transmission measurements, which to our knowledge display the pronounced maximum in the transmitted laser power (energy fluence) as a function of the laser input power (energy fluence). This maximum is possibly due to the fact that both excitation wavelengths are in resonance with the indirect optical transition of Si. Most of the published FCA articles on Si refer to longer wavelengths.

The applied FCA model is based on several assumptions:

• constant Fresnel reflection factors for the laser beams at the Si membrane interfaces (e.g., no intensity dependence),

• a laterally and axially homogeneous distribution of eh pairs in the laser-irradiated and probed volume (e.g., independent on the local laser beam intensity), thus decoupling the two absorption processes of this FCA model,

• two optically linear absorption processes, i.e., for eh pair generation and their excitation with negligible coherent two- or multi-photon absorption,

• an effective absorption coefficient $\alpha _\mathrm{eff}=\alpha _1+\alpha _\mathrm{FCA}$ (e.g., independent on the Si sample temperature),

• a constant linear absorption coefficient $\alpha _1$ (Beer’s law),

• an empirical ansatz for the absorption coefficient $\alpha _\mathrm{FCA}=n_\mathrm{eh}\sigma _\mathrm{eh}$ for FCA with, for example, $\sigma _\mathrm{eh}$ being independent on the eh pair temperature (cf., e.g., [3]), but dependent on the eh pair density (cf., e.g., [10]), and

• negligible FCA in the $0\le I_0\le I_\mathrm{c}$ region with $I_\mathrm{c}$ being a critical minimum value up to which laser excitation possibly does generate eh pairs but no FCA.

As a result, fitting the experimental data with the above FCA model revealed a power law $n\approx 2$ of $\alpha _\mathrm{FCA}=\kappa _n\cdot I^n$, which is confirmed by the linear plots in Fig. 4. A physical interpretation of $n\approx 2$ is given by assuming that the stationary density $n_\mathrm{eh}$ of free charge carriers is proportional to the incident laser intensity $I_0$ and that the absorption cross section $\sigma _\mathrm{eh}=\sigma _0 n_\mathrm{eh}$ is proportional to $n_\mathrm{eh}$ [6] yielding the FCA absorption coefficient $\alpha _\mathrm{FCA}=\kappa _2 I_0^2$. However, there is a need for further experimental data to test the FCA model in more detail.