1 Introduction

During the last decade, very different systems demonstrating quantized behavior have been tested with respect to their suitability as hardware for implementation of quantum technologies [1]. The central problem is to find the balance between the possibilities of “closing” the quantum system as required for maintaining the coherence as good as possible, and “opening” it as needed for efficient manipulations and extracting information. The interest in solid-state systems has been triggered by potential advantages such as robustness, integrability, and scalability [2, 3]. Focusing on semiconductors has appeared particularly appealing because of established technology platforms to fabricate devices and the possibility to connect them to classical information processing components [4, 5].

The crystal environment offers a multitude of excitations that may be used as quantum bits [6, 7]. These excitations may exploit the crystal properties to their favor. For example, in exciton complexes (bound electron–hole pairs), the oscillator strength of an electron–hole transition is integrated over all unit cells within their extension, leading to a giant dipole matrix element and allowing efficient optical manipulation. Vice versa, as a downside of being “open” to the crystal, optically injected exciton complexes undergo fast radiative decay if the coupling to the vacuum light field is not suppressed. Consequently, by now they are considered mostly as intermediate states for ultrafast manipulation of quantum bits.

Alternatively, resident spin excitations are considered as quantum bit candidates due to their (in principle) “unlimited” lifetime. From bulk crystal studies, it is, however, well known that free motion leads to fast spin relaxation [8]. Therefore, the spins must be confined in a system that is “closed” as much as possible. This can be provided, e.g., by localization at defect sites or in quantum dots. Obviously, such localized spins still cannot be isolated as well as atoms or ions. They remain susceptible to their environment, for example the background of the nuclei in the crystal lattice with which the carrier spins interact. The system still remains “open” to some extent. Here, we focus on carrier spins in self-assembled (In,Ga)As quantum dots that have been addressed quite intensely in the recent past.

Initially, fast progress was made studying the coherence and manipulation of carrier spins in dot structures [9, 10]. On one hand, it has become evident that optical methods involving pulsed lasers—also in combination with microwave radiation—provide excellent tools for orienting and rotating electron spins. The work on hole spins is still incomplete in this respect [11, 12]. On the other hand, it is also clear that such quantum dots cannot be isolated “in a closed system” to an extent that would bring spin coherence times into a range comparable to atoms. This is due to the enhanced hyperfine interaction with the nuclei, limiting ultimately the coherence to the microseconds range [13]. Moreover, any manipulation may not only affect the targeted spin, but also the surrounding which can lead to detrimental back-action. For example, ultrafast optical manipulation can affect the nuclear spins through flip–flop processes with the carrier spins, and the optical carrier injection leads to a lattice distortion associated with phonon emission [14, 15].

Furthermore, progress has also been hampered by complications in introducing a robust controlled interaction between spins, as required for technologies based on entanglement. First attempts focused on exploiting the short-ranged Coulomb interaction in tunnel-coupled quantum dot molecules [16, 17]. However, these approaches are difficult to scale up and require advanced control concerning spin occupation, coupling, etc. Other complications are the difficulty to obtain ultrafast coupling control for the interacting levels that are narrow spaced in energy. Therefore, it is hard to address them separately, besides the inhomogeneity due to the molecule structure variations.

As a consequence, not too many efforts have been undertaken to go beyond this level and obtain a more advanced level of spin manipulation. This is the goal that we target here by first discussing hole spin rotations through laser pulses. Then, we turn to efforts to use these spin rotations for the implementation of dynamic decoupling protocols in order to extend the coherence of hole spins. Subsequently, we will turn to electron spins, for which we will discuss a complete optical spin tomography exploiting these spin rotations. Finally, we will turn to advanced manipulation techniques for electron spins involving sequences of multiple laser pulses.

The peculiarity of all studies described here is the involvement of ensembles of singly charged quantum dots. The related inhomogeneity can be partly compensated by the mode-locking effect, i.e., by the synchronization of the spin precession about a magnetic field with the periodically pulsed laser excitation; for details, see Ref. [18].

2 Experiment

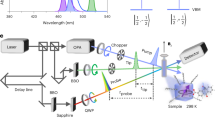
The basic experimental setting, which is then adjusted and extended for the specific needs of the different experiments, is based on a pump–probe setup in which a periodic train of circularly polarized pump pulses at time zero orients the spins parallel or antiparallel to the optical axis, chosen to coincide with the growth direction of the (In,Ga)As/GaAs quantum dot heterostructure and denoted here as z-direction. The spin orientation is measured by probe pulses with variable delay relative to the pump. These pulses—linearly polarized before transmission through the sample—are used to measure either ellipticity or Kerr rotation behind the sample, which is a measure for the spin polarization along the optical axis. Pump and probe are typically taken from the same laser oscillators.

The photon energy of the laser is in most cases tuned in resonance with the maximum of the inhomogeneous emission from the dot ensemble. As the dots carry an occupation of one resident electron or hole per dot, the laser drives the optical transition from the carrier to the corresponding charged exciton. The pulses taken from a Ti:Sapphire laser have a spectral width of 1 meV, corresponding to a pulse duration of about 2 ps. The pulse repetition rate is 75.8 MHz corresponding to a pulse separation of 13.2 ns. The pulse separation can be elongated by using the first diffraction order of an acousto-optical pulse picker. For studying the spin dynamics, a transverse magnetic field normal to the optical axis is applied. The field direction is denoted as the x-axis in the following.

For obtaining spin rotations about the optical axis, an additional Ti:Sapphire laser synchronized to the first one with an accuracy below 1 kHz is employed. The central wavelengths of the different oscillators can be tuned independently as can be the emitted intensity levels.

3 Hole spin rotations

First, we will show the implementation of optically induced rotations of resident hole spins in quantum dots. So far, spin rotation by laser pulses was mostly performed on quantum dots containing resident electron spins [19, 20]. The main strategy is that rotation pulses (RPs) with an area of \(\varTheta _{\text {RP}}= 2 \pi \) are used so that no trion population is generated when driving the optical transition from the resident carrier to the corresponding trion. Therefore, the resident carrier spin is left in its quantum bit space. Through varying the detuning of the RP photon energy from the carrier–trion transition, different geometric phases for rotation about the optical axis, taken as z-axis, can be obtained. In particular, for fully resonant excitation, the RP leads to a rotation by angle \(\varPhi = \pi \). Here, we want to transfer this concept to hole spins.

The experiments are performed on a sample containing 11 electronically decoupled layers of self-assembled (In,Ga)As/GaAs QDs separated by 100-nm GaAs barriers. These dots are mostly p-doped due to carbon impurities. The PL ground state emission has its maximum at 1.38 eV with a FWHM of 19 meV at \(T=6\) K.

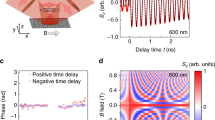
First, we seek for indications that hole spin rotation can be achieved. This is complicated by the fast dephasing of the spin coherent signal in the hole spin ensemble due to the strong inhomogeneity of the hole g-factor in combination with its small magnitude along the transverse field. In such an inhomogeneous spin ensemble with varying Larmor frequencies, successful spin rotation leads to spin polarization echoes if the rotation angle is greater than \(\pi /2\), because the dephasing process is inverted. Figure 1a demonstrates hole spin echoes as consequence of application of a RP at an applied magnetic field strength of 0.5 T. Shown is the ellipticity of the probe pulse as function of the delay relative to the pump pulse applied at time zero. Right after the pump which orients the spins along the optical axis, the spin coherent signal is given by a superposition of a fast oscillation component that we attribute to the electron spin precession about the magnetic field, and a slow component that arises from the resident hole spin precession [21]. Additional measurements of a full 3D behavior of the g-factor tensors support these assignments [22]. The signal disappears after about a nanosecond. This is a consequence of the fast dephasing due to the g-factor inhomogeneity, despite the small applied magnetic field applied on purpose to minimize the translation of g-factor variations into the precession frequency, \(\omega = g \mu _B B/\hbar \).

The fast dephasing can be seen also from the slowly oscillating signal at negative delays, which emerges from zero signal level before any additional pump pulse application and arises from mode-locking of hole spins to the laser repetition rate. As any optically pump-excited carriers have decayed at this time, this signal also demonstrates the resident doping of the quantum dots by hole spins.

Then, in addition, a rotation pulse is applied, whose separation \(\tau \) from the pump pulse is varied in the different traces. The photon energy in this case is resonant with that of pump and probe. The signature of a spin polarization echo is that after RP application at time \(\tau, \) a signal should be observed around delay \(2 \tau \). The different traces clearly confirm the formation of such an echo that shifts systematically with increasing \(\tau \).

Next, after hole spin rotation has been demonstrated, the power of the RP has to be adjusted to \(\varTheta _{\text {RP}} = 2 \pi \) such that it does not induce a trion population due to a full Rabi flop on the hole–trion Bloch sphere but only a geometric phase shift by an angle of \(\varPhi = \pi \) around the optical axis. Only then, hole spin rotations are performed without leaving the hole spin subspace [20]. Therefore, experiments are performed in which the average RP laser power is varied with fixed RP incidence time. The results are shown in Fig. 1b, where the photon energy of the RPs still coincides with that of pump and probe. The RP incidence is chosen to be at \(\tau =1.2\) ns delay, leading to echo formation at 2.4 ns.

The first signature would be a phase shift of the pump–probe trace by \(\pi \) relative to the trace without RP, which does not depend on the RP power in the ellipticity experiment as long as the spin rotation angle is larger than \(\pi /2\). This shift is, however, hard to assess due to the fast dephasing of the reference signal. The second signature is a maximum of the echo signal as any deviation from \(\varTheta _{\text {RP}} = 2 \pi \) reduces the signal due to the excited trion component and the corresponding reduction in the hole spin component. The data in Fig. 1b show no very pronounced dependence of the echo amplitude on RP power as a consequence of the strong hole spin inhomogeneity, but still it has a maximum for 80 mW power. In the following, we keep the RP power fixed at this level.

Fig. 1
figure 1

a Pump–probe ellipticity traces with additional rotation pulses arriving at different delays \(\tau \) marked by arrows. The spin rotation by an angle \(\varPhi > \pi /2\) leads to hole spin echoes at \(2\tau \). \(B=0.5\) T, \(T=6\) K. b Rotation pulses at \(\tau = 1.1\) ns with different laser powers \(P_{\text {RP}}\). The detuning between the pump–probe and the rotation laser was \(\varDelta =E_{\text {PuPr}}-E_{\text {RP}}=0\) meV so that for a pulse area of \(\varTheta _{\text {RP}}=2\pi, \) the echo is of maximal amplitude. This was found to be at \(P_{\text {RP}}=80\) meV

Full size image
Fig. 2
figure 2

a Detuning dependence of ellipticity traces with rotation pulses arriving at 0.3-ns delay when the hole spins are oriented perpendicular to the optical axis. The pulse area was chosen to be \(\varTheta _{\text {RP}}=2\pi \). For the degenerate case \(\varDelta =0\) meV, the rotation angle is \(\varPhi =\pi \) leading to an echo formation around 0.6-ns delay. For larger \(\varDelta, \) the rotation angle is reduced to \(\pi /2\) at ~1.3 meV. The upper trace shows a reference signal without application of rotation pulses. b Rotation angle \(\varPhi \) in dependence of the detuning \(\varDelta \). The data are obtained from the signal amplitudes at \(2\tau \) in a. The blue line is calculated according to \(\varPhi = 2 \arctan \left( \frac{\sigma }{\varDelta }\right) \) for a pulsewidth of \(\sigma =1\) meV

Full size image

The next step is to demonstrate hole spin rotations about the optical axis by an arbitrary angle. In combination with the hole spin precession about the magnetic field, it is then in principle possible to orient the hole spin vector along any arbitrary direction on the hole spin Bloch sphere. This shall be achieved by detuning the RP photon energy from the trion resonance [23]. This is shown in Fig. 2a. Due to the fast dephasing, the RP incidence \(\tau \) is chosen at 0.3 ns, shortly after the pump incidence at a delay where the net hole spin polarization is pointing along the y-direction, perpendicular to the optical axis z and the field axis x. For zero detuning (\(\varDelta =0\)) of the RP from the pump, the spin polarization echo therefore appears at \(2\tau =0.6\) ns.

By detuning the RP photon energy, the echo amplitude decreases because the net spin polarization is partly rotated out of the precession plane. At \(\varDelta = 1.5\) meV, the rotation angle is \(\pi /2,\) and the hole spins are rotated to point along the magnetic field direction so that they do not precess anymore. Hence, the hole spin oscillations vanish after rotation. For larger detunings, the rotation angle decreases below \(\pi /2\) so that no echo is formed, and the achieved rotation cannot be traced anymore. For rotation angle \(\varPhi < \pi /2\), however, the exact rotation angle can be determined by the normalized hole spin signal amplitude A at \(2\tau =0.6\) ns, assuming a full \(\pi \) rotation at zero detuning. The angle is then simply given by \(\varPhi = \arccos (A)\). These angles are plotted in panel (b) of Fig. 2 together with a calculated curve according to the model estimation \(\varPhi = 2 \arctan \left( \frac{\sigma }{\varDelta }\right) \) [23]. These results confirm that indeed hole spin rotations can be achieved, at least as long as the spin dephasing has not become too detrimental.

4 Dynamic decoupling of hole spins

In a next step, the potential of such hole spin rotations for more complex coherent operations shall be explored. One problem in this respect is the implementation of dynamic decoupling protocols. In general, such protocols lead in effect to a reduction in the coupling to the environment, so that the coherence of a quantum mechanical state is maintained over longer times. This is particularly interesting for quantum-dot-confined spins, for which transverse relaxation (coherence) times \(T_2\) in the microsecond range were measured, while the longitudinal relaxation time \(T_1\) may be in the millisecond range [24, 25]. Therefore, there is room for increasing the spin coherence time by orders of magnitude.

The basic idea of such protocols is to invert the spin orientation by repeated application of \(\pi \) rotation pulses so often that the spins in effect are no longer exposed to destructive effects from the environment. Applying multiple \(\pi \) rotations in short intervals compared to the coherence time \(T_2\), the coupling to the surrounding baths is in effect averaged to zero [26]. Dynamic decoupling methods are well established in NMR after the original proposal in Ref. [27] for microwave pulse sequences [28–31]. Here, quite some development has occurred moving from the original protocols involving periodically repeated single pulses to much more complex pulse sequences. Optically, however, until now no dynamic decoupling protocol could be implemented. The optical approach has the advantage of shorter pulses, so that the inversion pulses can be applied at a higher repetition rate. As a consequence, the gap of frequencies to which the spin quantum bit is insensitive is increased.

An implementation of such an optical dynamical decoupling protocol by repeated single pulses is demonstrated in Fig. 3. Panel (a) shows a schematic illustration of the pulse sequences used in the experiment. Between two subsequent pump pulses (black), an RP train (red) with a frequency that is an integer multiple of the pump pulse repetition rate is applied. For better illustration, the pump pulse period in the sketch is \(T_{\text {R}}=12\, T_{\text {RP}}=79.2\) ns, so that the individual RPs between two pump pulses can be recognized. In the experiment, we used \(T_{\text {R}} \ge 20\, T_{\text {RP}}=132\) ns. With a pulse area of \(2\pi \) and being in resonance with the pump excitation energy, the RP flip the spins’ y component and invert the dephasing process. This leads to an echo signal from the spin polarization induced either initially by the pump or from the last echo, respectively. The resulting echo pattern is given by the blue upper trace in panel (a). Due to the integer ration between pump and rotation pulse repetition rate, an echo appears also around the times of pump incidence. In addition, since the echo pattern is symmetric around any RP incidence, an echo appears 2.2 ns before pump incidence for an RP incidence 1.1 ns before the pump [32]. This is shown by the upper, blue trace in Fig. 3b where we focus on the 3-ns range before a pump pulse. Without RP application (lower, black trace), no echo emerges and only the signal of mode-locked resident hole spins (see next section) can be seen right before pump incidence.

Without RP application, the coherence time was determined to be 0.6 \(\mu \hbox {s}\), see the black dots in panel (c). This coherence time was extracted from the amplitude of the mode-locked hole spin signal right before the pump pulse. If the pump pulse separation is on the same scale as the hole spin coherence time, the amplitude of the mode-locked signal drops, and from the decay time (as determined by an exponential fit), the spin coherence time can be derived, see also next section.

In case of application of a dynamic decoupling sequence, the dependence of the amplitude of the last echo before pump incidence on the time elapsed after pump pulse separation can be used for estimating the coherence time. Also here a decay is observed which is plotted as blue squares in Fig. 3c for an RP separation of 6.6 ns. While without the RP pulse sequences the amplitude decay can be well described by an exponential decay, this is no longer the case when dynamical decoupling is targeted. Using nevertheless such a form gives a decay time of 1.2 \(\mu \hbox {s}\) which would correspond to an enhancement of the hole spin coherence time by a factor of 2. However, a better description of the data is achieved by a bi-exponential decay form consisting of a initial fast decay followed by a subsequent slow decay. For this slow component, the corresponding fit gives decay times on the order of \(10\mu \hbox {s}\). This would correspond to an extension of the spin coherence time by much more than an order of magnitude. The additional source of decoherence responsible for the fast decay is most probably provided by the laser pulses themselves. As it was found in Ref. [33], there is additional dephasing of the bound-exciton state proportional to applied pulse power. This dephasing may be due to local heating via background absorption of the laser, which induces some population of phonons or other excitations, such as excited impurity states.

On one hand, this shows the great potential that dynamic decoupling protocols implemented with optical pulses have for extending the spin coherence. On the other hand, at the moment, it seems hardly feasible to implement corresponding protocols that are composed of more complex laser pulse sequences than just periodic repetitions. It will be hard to achieve similarly complex multi-pulse sequences as in NMR.

Fig. 3
figure 3

a Schematic illustration of pump pulse incidences (black, at \(T_{\text {R}}=79.2\) ns), RP incidences (red), and echo appearances (blue). b Ellipticity traces at a pump repetition period of \(T_{\text {R}}=132\) ns with and without application of rotation pulses (RP) at a period of \(T_{\text {RP}}=6.6\) ns. The RP incidence within the monitored time range is marked by the red arrow at \(-1.1\) ns. A hole spin echo can be observed at \(-2.2\) ns delay (blue). c Normalized ellipticity amplitudes of the last echo before pump incidence (blue squares) and of the mode-locked signal amplitude right before pump incidence (black dots) in dependence of the pump pulse separation \(T_{\text {R}}\). The curves are fits to the data according to Eq. (2) providing coherence times of \(T_2=1.2\) \(\mu \hbox {s}\) and \(T_2=0.6\) \(\mu \hbox {s}\), respectively

Full size image

5 Spin coherence in magnetic field

As indicated in the previous section, the standard tool to measure spin coherence time \(T_2\) has been the mode-locking effect described in Ref. [18]. In short, when the spin coherence time is longer than the pump pulse period \(T_{\text {R}}\), the net spin polarization vanishes on the timescale of inhomogeneous dephasing but reemerges before the next pump excitation due to constructive interference of spin precession modes that fulfill the phase synchronization condition

$$\begin{aligned} \omega _\mathrm{{L}}= N \frac{2\pi }{T_\mathrm{{R}}} \, . \end{aligned}$$
(1)

If the pump pulse period \(T_\mathrm{R}\) becomes comparable to the coherence time \(T_2\), the amplitude of the mode-locked signal before pump incidence as function of \(T_\mathrm{R}\) is given by:

$$\begin{aligned} S_z (T_{\text {R}})= A \exp \left[ -\left( 2+\frac{1}{2\sqrt{3}+3}\right) \frac{T_{\text {R}}}{T_2} \right] \, . \end{aligned}$$
(2)

By increasing the pulse period and monitoring the spin signal amplitude, the coherence time can therefore be determined which has been used in the past to assess the \(T_2\) time for electron and hole spins, also for varying temperatures [24, 34]. In both cases, the limitations of \(T_2\) to the microsecond range are attributed to the interaction with the nuclei. In particular, the nuclear spin bath, which is frozen for shorter times, is expected to fluctuate on these timescales affecting also the carrier spin coherence.

Observation of mode-locking requires application of a magnetic field about which the spins precess. As shown before, the mode-locking effect is also contributed by nuclear focusing of spin precession modes onto the phase-synchronized modes by buildup of the required nuclear field [35]. This focusing works well for electron spins, while for the hole spins no indications of nuclear focusing could be observed [36]. This, however, should influence only the amplitude of the mode-locked signal and not its lifetime, as the required nuclear spin polarization for fulfilling mode-locking is quite small so that the nuclear system is not transferred to a strongly ordered state with correspondingly reduced fluctuations.

The field leads to a spin splitting of the nuclei, but without dedicated nuclear pumping, all nuclear spin levels should be thermally occupied equally at the used temperatures which are in the high-T limit. The larger the field, the stronger is the mismatch between the Zeeman splittings of nuclei and carrier spins, so that corresponding flip–flop processes could be suppressed more in a steady-state situation. However, after excitation, the carrier spins are anyway in a superposition state of the two eigenstates during their precession in a magnetic field. Therefore, the expected behavior is far from being trivially clear.

Figure 4 shows corresponding measurements of electron and hole spin coherence time as function of the applied magnetic field. The sample used for the studies on resident electron spins contains 20 layers of self-assembled (In,Ga)As/GaAs QDs separated by 80-nm wide GaAs barriers. A Si-\(\delta \)-doping sheet beneath each layer provides in average one resident electron per dot. The ground state emission of the PL spectrum is at 1.393 eV. For the hole spin studies, the sample is the same as used before. For both electron and hole spins, a decrease in the coherence time is observed with increasing magnetic field. The decrease is much more pronounced for the holes than for the electrons: For the electron spins, the decrease is by a factor of about 2, and for the hole spins, the reduction is given by a factor of 5. For sufficiently high fields, the coherence time tends to become constant.

In the standard description, at zero external field the carrier spins precess about the frozen nuclear spin fluctuation field (Overhauser field) with a typical strength of tens of mT [13]. Vice versa, the nuclear spins precess on a much slower timescale about the electron spins. In our situation, the effect of the external field has to be accounted for. The resulting precession of the nuclei about the external field leads to an accelerated fluctuation of the Overhauser field. We tentatively assign this fluctuation to the decrease in the carrier spin coherence time. At high fields, the nuclear precession is accelerated to an extent that the electron and hole spins are exposed to a constant average field and the field dependence in effect vanishes. The electron spins are likely less sensitive to the nuclear spin fluctuations due to precession, as their precession is about a factor of four faster than that of the holes. This could lead to a dynamical averaging of the nuclear spin fluctuations. However, clearly the details of the magnetic field dependence of the electron and hole spin coherence times are not understood yet.

Fig. 4
figure 4

Normalized spin coherence time \(T_2\) versus magnetic field B for electron (a) and hole spins (b)

Full size image

6 Electron spin tomography

Standard pump–probe techniques for measuring Faraday or Kerr rotation give access only to the spin component along the optical axis z. Through the coherent spin precession in a magnetic field normal to the optical axis, access to the spin components in the plane perpendicular to the field can be accessed. However, no information is available for the spin component along the magnetic field. Such information can be gained though, if a rotation pulse is applied rotating the component along the field into the plane normal to it so that it undergoes subsequently precession which can be traced through magneto-optical effects.

On the other hand, knowledge about any spin component along the magnetic field is not necessary in pump–probe experiments in a normal field, in which the pump orients the spin and the probe tests it. In such experiments, the corresponding component disappears. However, knowledge about a spin component along the magnetic field is necessary if an interaction between spins exists, which in many cases can be described by a Hamiltonian of Heisenberg- or Ising-type [37]. The presence of such an interaction will cause a precession of the spins about each other, even if the spins are oriented by the pump at time zero parallel to each other, as long as they precess at different frequencies about the external field. In such a case, a spin tomography measurement to determine all spin components is required. And as the carrier spin dynamics occurs on a nanosecond timescale or even faster, an all-optical approach is needed.

Let us consider the details of the tomography measurement in a bit more detail: Obviously, the measurements of the spin components have to be taken subsequently. Furthermore, all manipulations during the tomography need to be performed such that spin coherence is maintained. The z- and y-components of the spin vector are mapped by probe pulses applied at variable delay after the pump incidence. For tracing the x-component, an additional optical rotation pulse about the optical axis by an angle of \(\varPhi = \pi /2\) has to be applied between pump and probe. The moment of rotation has to be timed precisely with respect to the phase of precession. When the z-component is zero, the residual y-component is rotated in the x-component where it stops to precess. Then, only the former x-component contributes to the probed precession signal. When the net spin polarization in an ensemble has dephased completely, the situation is more simple. Since the x-component is not subject to inhomogeneous dephasing, the signal contrast does not depend on the exact moment of RP incidence. From previous experiments, parameters of the RP were chosen such that a \(\pi \)/2-rotation is achieved by appropriate detuning of the photon energy in combination with a \(2\pi \) intensity to perform pure rotations.

Such a tomography experiment is performed on a subset within an ensemble of negatively charged QDs [38]. This subset is interacting with another spin subset in the same QD ensemble [39]. Both subsets are oriented antiparallel to each other by 1-meV wide pump pulse trains spectrally separated by 6 meV, to avoid any spectral overlap. As a consequence of this, a Heisenberg-like interaction is established between the two spin subsets, so that each spin vector describing a subset develops a spin vector component along the magnetic field. For details on the characteristics of this interaction, please refer to Ref. [39].

Figure 5a shows two time-resolved ellipticity traces testing the precessing spin polarization of subset 1. The blue (dark) reference trace shows the case without optically generated spin polarization in subset 2. In the measurement provided by the red (bright) trace, the second subset was spin-oriented along \(-z\) with a delay of 1.3 ns after the first one when the spins of subset 1 point long \(+z\). The probe photon energy is tuned in resonance with pump 1 and does not capture any direct influences from the spin subset 2.

Fig. 5
figure 5

a Time-resolved ellipticity measurement of the spin polarization oriented by pump 1 with an additional spin rotation about the optical axis by an angle of \(\varPhi =\pi /2\) at 7-ns delay for two cases: with application of a second pump orienting another spin subset at 1.3-ns delay antiparallel to the first subset (red) and without application of pump 2 (blue). \(B=0.3\) T, \(T=6\) K. b Time evolution of the x-component of spin subset 1 under the influence of a spin–spin interaction with the second spin subset oriented by pump 2

Full size image

During the first 6 ns after pump incidence at zero delay, both ellipticity signals look similar, albeit some differences in the signal amplitude. At 6.2-ns delay, the RP rotates the electron spins in both cases by \(\pi /2\) about the optical axis. The blue trace recorded for the single oriented spin subset 1 shows no signal as consequence to that rotation, as expected since the pump pulse orients the spin along the optical axis and afterward the spins precess in the plane normal to the magnetic field. The red trace, however, shows clearly pronounced oscillations after RP incidence which result from the spin component that was formerly oriented along the x-axis due to the interaction between spin subsets 1 and 2.

From varying the hit time of the RP relative to the optical orientation time of spin subset 2, the buildup of the spin component as consequence of the spin–spin interaction can be traced. This time evolution is shown in Fig. 5b. The x-component rises and tends to saturate for the delays accessible in our experiment which are limited by the length of the optical delay line. For greater delays, a drop of the spin component along the magnetic field is expected since action of a Heisenberg-like interaction is ultimately expected to result into a fully entangled Bell state of the two spins with zero total spin.

The described studies have shown that it is possible to perform a full spin tomography by all-optical tools. For the specific application for which we have implemented, one would have ideally also measured the spin vector of the second spin subset. Here, the limitations of the approach become clear as it involved already three synchronized Ti:sapphire laser oscillator, two for orienting the spin subsets 1 and 2 by pump pulses and the third one for providing the rotation pulse. Simultaneous spin tomography of the subset 2 would require a fourth laser oscillator to perform the required spin rotation. In addition, also the experimental conditions set limitations, as one cannot bring the photon energies of the different lasers too close as they would otherwise influence both spin subsets. Furthermore, care has to be taken that the laser do not excite, for example transition involving excited states in the quantum dots.

7 Multipulse spin manipulation

In pump–probe experiments, a rather simple dynamics is “imprinted” on the spin ensemble that can be perfectly well described by harmonic functions. This dynamics can be shaped in a much more complicated way by applying not only a single, circularly polarized pulse, but multiple of such pulses, for which we assume the same photon energy. Here, we consider pump pulse doublets. After a spin has been oriented by a first pulse, the possibility to perform another excitation by a second pulse depends strongly on the spin orientation of the resident carrier during precession. Let us consider a right circularly \(\sigma ^+\) polarized pulse which due to the optical selection rules would inject for a \(\pi \)-pulse intensity an electron–hole pair with electron spin down and hole spin up. However, if the resident spin of either electron in n-doped dots or hole in p-doped dots is identical to the one targeted through optical injection, Pauli blockade prevents this excitation. In all other cases, a superposition state of the non-excitable resident spin component and a trion state is created.

For a single spin, this leads to reorientation or reduction in the spin orientation. More interesting is the ensemble case when the second pulse hits the ensemble at time where ensemble dephasing has occurred. Let us consider the time exactly between two first pump pulses in the pump sequences. Simply speaking the resident spins can be divided then into those with projection onto the optical axis such that it can no longer be excited due to Pauli principle, while the other ones can be excited into trions and therefore the corresponding spin polarization is annihilated. The second pump pulse therefore acts as a rectifier on the spin polarization dephased ensemble as the component of particular sign is cut off. As a consequence, the spin polarization can be no longer described by a simple harmonic with some broadening, but the Fourier transform of the periodic signal is expected to contain higher harmonics.

This double-pump experiment was implemented such that the second rectified pulse was shifted in parallel with the probe relative to the first pump pulse. The black trace in Fig. 6b is a reference ellipticity without the rectifier applied in an external magnetic field of \(B=1\) T. The signal shows dephasing and rephases before the next pump pulse arrival at \(T_{\text {R}}=13.2\) ns due to mode-locking. The red trace shows the ellipticity with the rectifier applied. The signal between dephasing and rephasing is strongly changed when the rectifier pulses are applied. Clearly new coherent signals emerge. The lower panels show close-ups of the ellipticity around particular delays, demonstrating that indeed higher harmonics of the basic single spin precession frequency are observed. In particular, the double precession frequency is observed at times about half of the pump pulse separation. The triple frequency is seen at one-third and two-thirds of the pump separation. And at one-fourth and three-fourths of the separation, even the quadruple frequency is observed.

Fig. 6
figure 6

a Simplified sketch showing the spin precession of the lowest six modes synchronized with the laser repetition rate. The arrow arrangements illustrate the spin orientations around specific delays which turn out to be specific fractions of the repetition period \(T_{\text {R}}\). b Ellipticity measurements without (black, lower trace) and with rectifier application (red,upper trace). \(B=1\) T, \(T=6\) K. c–f Close-ups of the time ranges indicated in (b)

Full size image

The top panel gives a sketch aimed at explaining why the different harmonics appear at particular delay times. As described before, the precession frequencies are locked to particular modes. Around the times where strong coherent signal bursts occur, the mode-locked frequencies show interfere constructively and form particular patterns, as indicated by the arrow arrangements below in Fig. 6a. For demonstrational purposes, the oscillations of the six lowest possible mode-locked frequencies are shown. In experiment, the spins typically perform at least an order of magnitude more oscillations between two pump pulses. The spin patterns at the particular times of spin bursts resemble somewhat wind mills with varying number of blades, equal to the harmonics order that is observed in the spin precession. The reorientation of specific “blades” by the second pulse leading to the described rectification effect leads to the appearance of the harmonics in the precession of the whole spin ensemble [40].

8 Summary and outlook

We have given here particular examples of optical spin manipulation beyond the level of orienting spins and measuring coherence. While some progress has been achieved in advanced spin control, also the related difficulties have become clear due to the limited flexibility of tailoring laser pulse protocols with respect to the pulse frequency, power, duration etc. While steady progress is made in obtaining more powerful, versatile and compact lasers at the moments, it seems unlikely that a similar level of pulse control can be achieved as for microwaves. For example, it seems unlikely that the pulse sequences emitted by the laser oscillators can be altered in time on short timescales.

Therefore, one may seek for complementing the optical methods by “electrical” techniques. This has been done already partly by employing microwave pulses for spin manipulation. Another possibility would be to keep the pulsed laser oscillator operation fixed and use electric field gates such that the optical transition energy is varied with respect to the laser photon energy. Such a variation is necessary, for example, for obtaining spin rotations with variable rotation angle. The applied voltage protocols may be adjusted in a more flexible way and on shorter timescales then laser pulse sequences.

As a first step in that direction, we have fabricated structures in which the loading of the dot structures with resident carriers is not done stochastically by doping but in a deterministic fashion through the gates. The sample contains a single layer of (In,Ga)As/GaAs n-doped QDs surrounded by (Al,Ga)As barriers. It is covered by semitransparent titanium gates and gold contacts. By applying electrical gate voltages, it is possible to change the charging state of the QDs. The charging state is mapped out by pump–probe spectroscopy.

Figure 7 shows a series of Kerr rotation traces for different applied gate voltages U. At negative voltages \(U<-0.6\) V, no indications of significant spin oscillations are found, indicating that the dot structures are empty and photoexcited carriers also quickly tunnel out of the dots. With increasing voltage pronounced, long-lived oscillations appear and become more prominent up to voltages of \(U=-0.4V\). The precession frequency corresponds well to the electron g-factor expected in these structures. Namely, an electron spin g-factor \(g_{\text {e}}=0.544 \pm 0.001\) is derived. Increasing the gate voltage further leads to a rather abrupt switching from the fast oscillating precession to one with low frequency, indicating that the quantum dots are now loaded by holes at \(U= - 0.2\) V. For even higher applied gate voltages, the observed oscillations become weak again and are short-lived, so that any spin precession is due to optically excited carriers, while there is no resident spin occupation. Panel (b) shows a close-up of the spin precession signal at a voltage of \(U=-0.5\) V. The Kerr rotation signal shows in particular a pronounced oscillation from mode-locked spins at negative delays.

Fig. 7
figure 7

a Time-resolved Kerr rotation for different gate voltages U at \(B=2\) T, \(T=6\) K. The pump–pulse separation is \(T_{\text {R}}=13.2\) ns. b Signal recorded for longer integration times at a gate voltage of \(U=-0.5\) V. At negative pump–probe delays, the signal oscillations are due to mode-locked resident electron spins

Full size image

These results demonstrate the potential of applying gates to control spins in quantum dots, using hybrid optical-electrical techniques. However, in a next step, gate voltage pulses need to be applied to obtain a truly coherent manipulation. Ideally, these pulses should have durations down to 10 ps or even shorter, which represents a considerable technological challenge, if such pulses are guided from a pulse generator down to the semiconductor chip inside a cryostat.

If this can be achieved and if the possibilities for advanced coherent spin manipulation can be advanced in that way, spins in quantum dots may be relevant for quantum information technologies, even though their coherence times may remain too short to serve as long-lived quantum information storage. However, for short-lived storage such that the information is available in devices for entangling quantum bits or distilling quantum information as required in quantum relays or quantum repeaters, the coherence times may turn out to be sufficient.