Abstract
We study multi-parameter solutions of the inhomogeneous paraxial wave equation in a linear and quadratic approximation which include oscillating laser beams in a parabolic waveguide, spiral light beams, and other important families of propagation-invariant laser modes in weakly varying media. A “smart” lens design and a similar effect of superfocusing of particle beams in a thin monocrystal film are also discussed. In the supplementary electronic material, we provide a computer algebra verification of the results presented here, and of some related mathematical tools that were stated without proofs in the literature. We also demonstrate how computer algebra can be used to derive some of the presented formulas automatically, which is highly desirable as the corresponding hand calculations are very tedious. In numerical simulations, some of the new solutions reveal quite exotic properties which deserve further investigation including an experimental observation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this article, we study multi-parameter laser modes in (linear) paraxial optics with the help of computer algebra methods by using an analogy with quantum mechanics. In particular, the Ermakov-type system’s approach to generalized quantum harmonic oscillators is utilized to paraxial, or parabolic, wave equations in a weakly inhomogeneous lens-like medium. Although several different techniques are widely available for integrating the (scalar) parabolic equations (see, for instance, contemporary reviews [3, 74, 124, 131, 140, 152] and the references therein), we would like to explore a variant of the Fresnel integral and a certain generalization of the lens transformation [97] combined with explicit solutions of the Ermakov-type system introduced in [90] as an alternative to the traditional ABCD law of paraxial optics [73, 74].
Knowledge of solutions of this system is particularly useful as they describe the propagation of Gaussian beams through various optical elements and devices that are subject to a noisy environment. We demonstrate that this approach gives a natural mathematical description of other special laser modes in optical systems under consideration. In the spirit of a modern “doing science by a computer” paradigm, a computer algebra derivation of all main results is given in the form of a Mathematica notebook [80], with the aid of algorithmic tools presented in [75–77]. One specific aim of this paper is to advertise and propagate the usage of computer algebra methods in physics. Our intention is to convince the reader that, in many instances, tedious hand calculations and longish proofs can be replaced by “pressing a button”.
For example, today’s computer algebra systems—like Mathematica which we utilize in this work—are powerful enough to verify that the expression
which corresponds to Eq. (3.6) below, is a particular solution of the time-dependent Schrödinger equation \(i\psi _{t}+\psi _{xx}=0\). Note that this verification is done on a completely symbolic and rigorous level, working with the symbolic parameters \(\alpha , \beta , \delta ,\;{\text {and}}\;\varepsilon\). In this instance, it suffices to enter the definition of \(\psi (x,t)\) and the expression \(i\psi _t+\psi _{xx}\) into the computer and employ the command FullSimplify; the result is 0, as expected. In other examples, one needs to assist the computer algebra system in the simplification task, as explained in the main part of the paper. A different approach, which is also presented here, consists in automatically deriving a differential equation satisfied by a given expression. In our example, this means that from the input expression \(\psi (x,t)\) above, the computer is able to derive the equation \(i\psi _t+\psi _{xx}=0\), using algorithms implemented in the HolonomicFunctions package [76]; more details on this example are given in Sect. 4.
In general, (multi-parameter) laser modes describe the beam deviation from the optical axis and an oblique propagation in the optical system, which is usually not discussed in the literature. They also correspond to the maximal kinematical invariance groups of the paraxial wave equations. We believe that all these new features may help the reader to use this approach in numerical simulations, as well as in the future experiment design and observations. The computer codes for all fundamental laser modes in question are provided, which may stimulate a new interest to this classical topic in paraxial optics.
For a more traditional approach to the paraxial wave equations and for their numerous applications in optics and engineering, the reader can be referred to the classical accounts [3, 9, 12, 16, 27, 28, 48, 50, 55, 74, 124, 128, 141, 143, 144, 146, 147, 151, 152]. The interested reader is referred to [9, 44, 50, 61, 91, 103] for further details on the transition from Maxwell to paraxial wave optics; see also [5, 6, 82, 138], and [148] for different aspects of geometrical optics and paraxial approximation in the diffraction theory. Among contemporary topics, a modern status of the concept of photon, second quantization, photon spin, helicity, and angular momentum are discussed in [24, 25, 63–65, 81, 87, 112]; see also the references therein. Gaussian light packages, that are highly localized in space and time, are investigated in [69–71].
The article is organized as follows: In the next section, we discuss basics of our approach, including the Green’s Function and Fresnel Integrals, as well as the derivation of the above-mentioned Ermakov-type system. This is followed, in Sect. 3, by a review of various multi-parameter laser modes and some of their applications. In Sect. 4, we explain the computer algebra tools employed in this article. Useful vectorial solutions of Maxwell’s equations in paraxial approximation are derived in appendices. Our numerical simulations, see [80], reveal some quite exotic properties of the laser modes under consideration. We believe that they deserve an experimental verification in some spectacular 2D and 3D experiments on the beam propagation.
2 Green’s function and Fresnel integrals for inhomogeneous media
This section comprises a brief survey of results established in [33, 45, 90, 97, 100, 132, 133] (see also the references therein for the classical accounts) which are composed here in a compact form in order to make our presentation as self-contained as possible. In addition, we present independent proofs in the supplementary electronic material [80] for the reader’s benefits. In the context of paraxial optics, this approach, among other things, allows one to unify various laser modes introduced and studied by different authors (a detailed bibliography is provided below but we apologize in advance if an important reference is missing.)
2.1 Unidimensional case
Recent advances in quantum mechanics of generalized harmonic oscillators can be utilized in order to solve similar problems concerning the light propagation in a general lens-like medium [45, 48, 73, 74, 83, 86, 97, 100, 123].
2.1.1 Green’s function and generalized Fresnel integrals
In the context of quantum mechanics, the 1D linear Schrödinger equation for generalized driven harmonic oscillators,
(a, b, c, d, f, and g are suitable real-valued functions of the time t only), can be solved by the integral superposition principle:
where Green’s function G(x, y, t) is given by
for suitable initial data \(\psi (x,0) =\varphi (x)\) (see [33, 90, 133] and the references therein for more details.)
The functions \(\alpha _{0}, \beta _{0}, \gamma _{0}, \delta _{0}, \varepsilon _{0}\), and \(\kappa _{0}\) are given by [33, 133]:
and
provided that \(\mu _{0}\) and \(\mu _{1}\) are the standard (real-valued) solutions of the characteristic equation:
with varying coefficients
subject to the initial conditions \(\mu _{0}(0) =0,\mu _{0}^{\prime }(0) =2a(0) \ne 0\;{\text{and}}\;\mu _{1}(0) \ne 0,\mu _{1}^{\prime }(0) =0.\) The Wronskian of these standard solutions is given by
Our coefficients (2.4)–(2.9) satisfy the so-called Riccati-type system, see the unidimensional case of Eqs. (2.41)–(2.46) below with \(c_{0}=0\) [90], subject to the following asymptotic expansions
as \(t\rightarrow 0.\) As a result,
Here, \(f\sim g\) as \(t\rightarrow 0,\) if \(\lim _{t\rightarrow 0}\left( f/g\right) = 1\). (For applications, say to random media [120, 136], the integrals are treated in the most general way which includes stochastic calculus; see, for example, [111].)
Note Most of these results were only stated in the original publications because its detailed calculations are pretty messy and time-consuming without use of algorithmic tools. In this article, for the reader’s benefits we present systematic computer algebra proofs of these results [80].
In the context of paraxial optics, when the time variable t represents the coordinate in the direction of the system optical axis, say s, for wave propagation, the expressions (2.2)–(2.3) can be thought of as a generalization of Fresnel integrals [8, 9, 27, 45, 55, 83–86, 100, 144]. The corresponding Schrödinger equation (2.1), with \(t\rightarrow s,\) can be referred to as a generalized paraxial or parabolic wave equation [97, 100].
2.1.2 Special beam modes in weakly inhomogeneous media
An important particular solution (generalized Hermite-Gaussian beams in optics) of the parabolic equation (2.1) is given by [90]:
where \(H_{n}(x)\) are the Hermite polynomials [110]. Here,
in terms of the fundamental solution subject to the arbitrary real or complex-valued initial data \(\mu (0) \ne 0,\, \alpha (0),\, \beta (0) \ne 0,\, \gamma (0),\, \delta (0),\, \varepsilon (0),\, \kappa (0)\). This solution was obtained in [90] by an integral evaluation, and its direct verification by substitution is provided in [80].
Note Equations (2.17)–(2.22) solve the one-dimensional case of the Ermakov-type system (2.41)–(2.46) below with \(c_{0}=1\) [90]; for the complex form of these solutions, see [81]; their verification is provided in [80].
By the superposition principle, (orthonormal) solutions (2.15) can be used for the corresponding eigenfunction expansions in the case of real-valued initial data. In our approach, the functions f and g are treated as two stochastic processes and Eqs. (2.7)–(2.9) and (2.20)–(2.22) can be analyzed by statistical methods [11, 120] (which may include random initial data.)
A solution in terms of Airy functions [50] (generalized Airy beams) has the form [98, 100]:
where
A direct verification is given in [80] for the reader’s benefits. Important special cases of Airy beams were found in [20, 125], and [126] (see also [98, 140] and the references therein; more details are given in Sect. 3.1 below.)
Note Equations (2.24)–(2.30) solve the one-dimensional case of the Riccati-type system (2.41)–(2.46) below with \(c_{0}=0\) [90]; a proof is provided in [80]. Moreover, in view of uniqueness of the Cauchy initial value problem for Schrödinger equation (2.1), the use of Green’s function (2.3) in Eq. (2.2) results in an integral evaluation for Airy functions which may have an independent value.
In general, one may interpret solutions (2.15)–(2.22) and (2.23)–(2.30), relating the initial and final parameters of the corresponding laser modes propagating in a certain element of optical device, as an alternative to the ABCD law which follows from the analogy between the laws for laser beams and the laws obeyed by the spherical waves in geometrical optics [73, 74]. As one can see, the corresponding composition laws will include a variant of linear fractional transformation when \(\alpha (0)\ne 0.\) A numerical example is discussed in Sect. 3.8. (Further details of this interpretation are left to the reader.)
2.2 Two-dimensional case
For the laser beam propagation in optics, the (co-dimensional) 2D case (with or without cylindrical symmetry) is of a great importance.
2.2.1 Separation of variables
In the paraxial approximation, a 2D coherent light field in a general lens-like medium with coordinates \(({\varvec{r}},s)=(x,y,s)\) can be described by the following equation for the complex field amplitude:
where \(H_{1,2}\) are the Hamiltonians in x and y directions similar to one in (2.1) but, in a general inhomogeneous medium model, with two different sets of suitable functions \(a_{1,2}(s),\, b_{1,2}(s),\, c_{1,2}(s),\, d_{1,2}(s),\, f_{1,2}(s),\;{\text {and}}\;g_{1,2}(s).\) (We assume, for simplicity, that the nondiagonal terms are eliminated by passing to normal coordinates.) The kernel of generalized Fresnel integral can be obtained as the product [100]:
where the kernels \(G_{1,2}\) are given by (2.3) with a simple change of notation: the coefficients \(\alpha _{0}^{(1,2)}\), \(\beta _{0}^{(1,2)}\), \(\gamma _{0}^{(1,2)}\), \(\delta _{0}^{(1,2)}\), \(\varepsilon _{0}^{(1,2)}\), \(\kappa _{0}^{(1,2)}\) are defined, in general, in terms of two sets of the fundamental solutions (2.4)–(2.9) with \(t\leftrightarrow s.\) The solution of the corresponding boundary value problem can be found by the integral superposition principle (2D generalized Fresnel integral):
for suitable initial data. (This integral determines the spatial beam evolution during the Fresnel diffraction.)
The corresponding 2D Hermite-Gaussian beams have the form
in terms of solutions of the Ermakov-type system (2.41)–(2.46) below with \(c_{0}=1,\) which are known in quadratures [90] (see also (3.9)–(3.14) for an important explicit special case). Equations (2.16)–(2.22) are valid with a similar change of notation for given initial data \(\mu ^{(1,2)}(0),\, \alpha _{1,2}(0),\, \beta _{1,2}(0)\ne 0,\, \gamma _{1,2}(0),\, \delta _{1,2}(0),\, \varepsilon _{1,2}(0),\, \kappa _{1,2}(0)\) (see also [10, 11, 55, 123, 144, 151, 152] for various special cases.)
In general, by the separation of variables, the product of any two 1D solutions (2.15) and (2.23), say
gives an important class of 2D solutions (Airy-Hermite-Gaussian beams in a weakly inhomogeneous medium; see also [58–60].)
2.2.2 Cylindrical symmetry
If \(a_{1}(s)=a_{2}(s)=a(s), \, b_{1}(s)=b_{2}(s)=b(s), \, c_{1}(s)=c_{2} (s)=c(s), \, d_{1}(s)=d_{2}(s)=d(s),\) the parabolic equation,
where \(f_{1,2}(s)\) and \(g_{1,2}(s)\) are real-valued functions of a coordinate in the direction of the optical axis s related to the wave propagation, can be reduced to the standard forms
by the following ansatz
(see Lemma 1 of [100], which is reproduced below in our notation with an independent computer algebra proof for the reader’s convenience).
Lemma 1
The nonlinear parabolic equation,
where a, b, c, d, \(f_{1,2}\) and \(g_{1,2}\) are real-valued functions of s, can be transformed to
by the ansatz (2.38), where \(\xi =\beta (s)x+\varepsilon _{1}(s)\), \(\eta =\beta (s)y+\varepsilon _{2}(s)\), \(\tau =\gamma (s)\), \(h=h_{0}a\beta ^{2}\mu ^{p}\,(h_{0}\) is a constant), provided that
Here,
and solutions of the system (2.41)–(2.46) are given by (2.24)–(2.30) and (2.16)–(2.22) for \(c_{0}=0\) and \(c_{0}=1,\) respectively.
Proof
For a computer algebra derivation, see the Mathematica notebook [80], which is available as a supplementary material on the article’s website. \(\square\)
In principle, our substitution (2.38) can be thought of as a generalized lens transformation in nonlinear paraxial optics (cf. [89, 107, 108, 135, 137, 146].) De facto, we have found a “proper” system of spatial coordinates \((\xi ,\eta ,\tau )\) which automatically takes into consideration “imperfections” of initial data and turbid medium in linear and quadratic approximations.
Note An algorithmic proof of the one-dimensional version of this lemma is given in [78].
3 Multi-parameter laser beams and their special cases
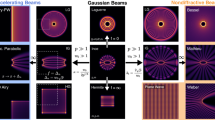
With the help of the generalized lens transformation described in Lemma 1 and available explicit solutions from quantum mechanics, one can analyze, in a unified form, a large class of multi-parameter modes for the corresponding linear parabolic wave equations in 1D and 2D weakly inhomogeneous media which are objects of interest in paraxial optics. Some of these solutions have been already demonstrated in recent laser experiments but others, which have quite exotic and spectacular properties according to our numerical simulations, yet deserve an observation.
3.1 Airy beams
In quantum mechanics, the time-dependent Schrödinger equation for a free particle (or the normalized paraxial wave equation in optics [45, 125] also known as the parabolic equation [50, 146]),
by the following ansatz
can be reduced to the Airy equation:
whose bounded solutions are the Airy functions \(F=k{\text {Ai}}(z)\) (up to a multiplicative constant k) with well-known asymptotics as \(z\rightarrow \pm \infty\) [50, 113].
The nonspreading Airy beams, which accelerate without any external force, were introduced by Berry and Balazs [20] (see also [21, 36, 57, 142] for further exploration of different aspects of this result). These nonspreading and freely accelerating wave packets have been demonstrated in both one- and two-dimensional configurations as quasi-diffraction-free optical beams [125, 126] thus generating a considerable interest to this phenomenon (see [1, 4, 13–15, 17, 18, 22, 30–32, 37, 38, 41, 66, 67, 92, 114, 116, 119, 140] and the references therein).
Equation (3.1) possesses a nontrivial symmetry [107]:
under the following transformation:
which is usually called the Schrödinger group, and/or the maximum (known) kinematical invariance group of the free Schrödinger equation (see also [16, 26, 36, 94, 95, 105, 108, 140] and the references therein; the subgroups and their invariants are discussed in [26, 98]; the group parameters \(\alpha (0),\, \beta (0),\, \gamma (0)=0,\, \delta (0),\, \varepsilon (0),\;{\text {and}}\;\kappa (0)=0\) are chosen as initial data of the corresponding Riccati-type system [94].)
As a result, in paraxial optics, the multi-parameter Airy modes are given by
as particular solutions of the parabolic equation \(iB_{s} +B_{xx}=0.\) (One can choose \(\gamma (0)= \kappa (0)=0\) in the explicit action (3.5) of the Schrödinger group without loss of generality.) The nonspreading case of Berry and Balazs [20] occurs when \(\alpha (0)=0\) in our notation. Other important special cases are discussed in [98, 125, 126] (see also the references therein). The direct verification by substitution and a computer algebra derivation of the parabolic equation for the beams (3.6) is given in [80] (see Sect. 4 for more details). Although nowadays Airy and related beams are well documented [1, 17, 23, 32, 37, 38, 92, 125, 126, 139], Fig. 1 represents an example of configuration which yet deserves the experimental observation. Our solution resembles, in the linear approximation, main features of rogue waves [68, 98, 127] (a simple animation is given in [80]).
Levels of intensity of the Airy mode (3.6) when \(\alpha (0)=-1/4, \beta (0)=1,\; {\text {and}}\;\delta (0)=\varepsilon (0)=0\)
3.2 Oscillating and breathing Hermite-Gaussian beams
For a 1D inhomogeneous paraxial wave equation with quadratic refractive index (a lens-like medium [73, 152]),
an important multi-parameter family of particular solutions can be presented as follows [88, 97]:
where \(H_{n}(x)\) are the Hermite polynomials [110] and
The real or complex-valued parameters \(\alpha _{0}, \beta _{0}\ne 0, \gamma _{0}=0, \delta _{0}, \varepsilon _{0}, \kappa _{0}=0\) are initial data of the corresponding Ermakov-type system [90, 94].Footnote 1 A direct Mathematica verification can be found in [80]. (A similar harmonic motion of cold trapped atoms was experimentally realized [93]).
These “missing” solutions that are omitted in all textbooks on quantum mechanics (see [95, 102]) provide a new multi-parameter family of oscillating Hermite-Gaussian beams in parabolic (self-focusing fiber) waveguides, which deserve an experimental observation; special cases were theoretically studied earlier in [10, 48, 50, 55, 73, 144, 151]. For graphical examples see Figures 1 and 2 of Ref. [97]. These modes are orthonormal for real-valued parameters. As a result, every \(L^{2}\) distribution of monochromatic light can be expanded in terms of these modes. The corresponding generalized coherent or minimum-uncertainty squeezed states are analyzed in [88].
3.3 Hermite-Gaussian beams
The homogeneous paraxial wave equation,
can be transformed by the substitution,
into the inhomogeneous one (3.7) (see [94] and the references therein; a Mathematica verification can be found in [80]). Composition of (2.15) and (3.16) results in the following multi-parameter family of “spreading” solutions to the parabolic equation (3.15):
for real or complex initial data [97]. The direct derivation is also provided in [80]. It is worth noting that both of our parameters \(\varepsilon _{0}\ne 0\) (shift) and \(\delta _{0}\ne 0\) (phase) describe, in a natural way, the beam deviation from the optical axis and a successive oblique propagation in an optical system, which is not usually discussed in detail in the literature. (This solution is also relevant to the concept of paraxial group [16] that comprises 2D transformations of a beam propagating through misaligned (tilted, translated, or rotated) ABCD optical systems).
Note When \(n=0,\) the intensity distribution \(\left| B_{0}(x,s)\right| ^{2}\) is normal in every beam cross section and the width of that Gaussian intensity profile changes along the s axis. The beam waist/focal point, when \(\nabla \left| B_{0}(x,s)\right| ^{2}=0\) and \(\max \left| B_{0}(x,s)\right| ^{2}=\sqrt{4\alpha _{0}^{2}+\beta _{0}^{4} }\ /\left| \beta _{0}\right| \sqrt{\pi },\) occurs at
In the limit \(\beta _{0}\rightarrow 0,\) we obtain the traditional definition of focus in the thin lens approximation [12, 144]:
The beam radius, related to standard deviation, is defined as the distance at which the amplitude is 1/e times of that on the mean [74]. Thus the smallest radius is observed at the focal point:
(Details are given in [80] together with a graphical example of “self-focusing” of the corresponding Gaussian mode “without any external force”.)
Among various special cases of these multi-parameter solutions are the so-called elegant Hermite-Gaussian beams. In our notation, they occur for the complex-valued parameters when \(4\alpha _{0}^{2}+\beta _{0}^{4}=0.\) The substitution
followed by \(2\alpha _{0}=i\beta _{0}^{2}\) results in
When \(n=0,\) one gets the multi-parameter fundamental Gaussian modes. In this case,
These optical fields obey a certain “propagation-invariant similarity rule”:
provided that
Thus, our solution describes an “oblique propagation” of the laser beam with respect to the optical axis (approaching the corresponding slanted asymptotes as \(s\rightarrow \infty ).\) For instance, the best confinement of optical energy occurs around the line \(x=\delta _{0}s,\) which becomes the direction of the beam propagation, when \(\varepsilon _{0}=0.\) This simple example shows how one can use our extra parameters in order to aim the laser beam and to maximize its intensity. A graphical example is provided in Fig. 2; see also [80] for more details.
Levels of intensity of the slanted beam (3.20) when \(\beta _0=2^{-1/2}\;{\text {and}} \;\delta _0=\varepsilon _0=1/2\)
Moreover, by the expansion transformation of the Schrödinger group [94]:
one arrives at the following Gaussian package:
(see also [80] for a direct verification). One may say that its spatial evolution also resembles the generation of an optical “rogue wave” which is appearing at a certain point and then dissipating. A graphical example of the intensity and optical energy localization is provided in [80].
Special families of Gaussian beams have found significant applications in science, biomedicine, and technology. Among them, the fundamental Gaussian mode described by Eq. (3.19), when \(n=0\;{\text {and}}\;\alpha _{0}=\delta _{0}=\varepsilon _{0}=0,\) is the most useful one. According to [3], the laser beams of this kind are utilized for the material cutting and surgery, for data reading in CD–DVD players and in optical remote sensing technology, and for microparticle trapping and atom cooling. Thus, telecommunication networks including the internet are based upon optical waveguide systems in which fundamental Gaussian modes are propagated in a wavelength multiplexing configuration.
In general, our multi-parameter solutions (3.17) can be thought of as the Hermite-Gaussian beams with “aberration/astigmatic elements” that are useful, for example, in the propagation of paraxial beams through a misaligned optical system (see Refs. [3, 7, 9, 12, 16, 74, 118, 123, 144, 149, 152] for further examples of these important modes in one and two-dimensions).
Note Although the multi-parameter elegant Hermite-Gaussian beams are not orthogonal, the corresponding integral:
can be evaluated in terms of generalized hypergeometric functions in a way that is similar to [88]. An investigation of certain minimization properties may be of interest.
3.4 Breathing spiral laser beams
By the ansatz \(\varPsi (x,y,t) =\chi (\xi ,\eta ,\tau ), T=-\tau\) and
(\(\omega =\hbox {constant}\)), Eq. (2.37) with \(c_{0}=1\) can be transformed to the equation of motion for the isotropic planar harmonic oscillator in a perpendicular uniform magnetic field:
The latter equation was solved in the early days of quantum mechanics by Fock [49] in polar coordinates, \(X=R\cos \varTheta \;{\text {and}}\;Y=R\sin \varTheta\):
\((m=\pm 0,\pm 1,\ldots, \,n=0,1,\ldots )\) in terms of Laguerre polynomials [110]. This wave function coincides, up to a simple factor, with the one for a flat isotropic oscillator without magnetic field. Therefore, its development in terms of (2.34) for standard harmonics is a 2D special case of the multi-dimensional expansions from [110] (see also [34, 104] and the references therein).
By back substitution, one arrives at a general family of spiral solutions in inhomogeneous media. For example, the 2D paraxial wave equation
possesses the following Laguerre-Gaussian modes [97]
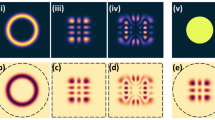
(by the action of Schrödinger’s group; see [94, 95, 100] and the references therein for classical accounts). Here, Eqs. (3.9)–(3.14) are utilized for complex or real-valued parameters \(\alpha _{0}\), \(\beta _{0}\ne 0\), \(\delta _{0}^{(1,2)}\), \(\varepsilon _{0}^{(1,2)}\) (the last two sets may be different for x and y variables, respectively). Examples are shown in Figures 3 and 4 of Ref. [97].
In addition, a special Gaussian form of our solution (2.34) gives a general example of spiral elliptic beams discussed in [55, 152].
3.5 Laguerre-Gaussian beams
The homogeneous parabolic equation,
with the help ofFootnote 2
can be reduced to the standard form (3.24). A multi-parameter solution is given by [97]
by the action of Schrödinger’s group. (The corresponding parameters are initial data of the Ermakov-type system (2.41)–(2.46); see Lemma 1).
Note An example of “self-focusing” Gaussian mode, when \(n=m=0,\) is presented in [80]. The corresponding focal point, when \(\max \left| B_{0}^{0}(x,y,s)\right| ^{2}=1+4\alpha _{0}^{2}/\beta _{0}^{4},\) is located at
It is worth noting that this mode describes the well-known effect of focusing of a laser beam in a uniform medium after passing the lens/quadratic medium. (In our approach, the quadratic, or lens-like, medium creates the corresponding initial data for the focusing beam, in a mathematically natural way).
For the set of complex-valued parameters, two special cases are of interest, namely the multi-parameter “elegant” Laguerre-Gaussian beams, when \(2\alpha _{0}=i\beta _{0}^{2}:\)
and multi-parameter “diffraction-free” Laguerre beams, when \(2\alpha _{0}=-i\beta _{0}^{2}:\)
For \(m=n=0\) and \(\varepsilon _{0}^{(1,2)}=0,\) this beam degenerates into the ordinary plane wave propagating in the direction \({\varvec{r}}=\left( \delta _{0}^{(1)},\delta _{0}^{(2)},1\right) .\) Polynomial solutions have also been discussed in [2] and [42].
Among numerous special cases are the Laguerre-Gaussian beams discovered in [19, 115, 144, 149]. By classical accounts [3, 9, 55, 74, 128, 151, 152] (see also the references therein), the families of the Hermite-Gaussian and Laguerre-Gaussian modes arise naturally as approximate eigenfunctions of the resonators with rectangular or circular spherical/flat mirrors, respectively. They also serve as models for eigenmodes of certain fibers. The introduction of astigmatic elements in optical resonators or after them leads to the generation of Hermite-Laguerre-Gaussian and Ince-Gaussian beams [122]. The Laguerre-Gaussian beams are also proposed for the applications in free space optical communications systems, where the information is encoded as orbital angular momentum states of the beam [54], in quantum optics to design entanglement states of photons [101, 106], in laser ablation [62], and in optical metrology [51], to name a few examples. Angular momentum of laser modes is discussed in [150].
3.6 Bessel-Gaussian beams
Use of the familiar generating relations
in (3.28) results in a new multi-parameter family of the Bessel-Gaussian beams:
(See [80] for an automatic verification). For the complex-valued parameters, among two interesting special cases are multi-parameter “elegant” Bessel-Gaussian beams, when \(2\alpha _{0}=i\beta _{0}^{2}:\)
and multi-parameter “diffraction-free” Bessel beams, when \(2\alpha _{0}=-i\beta _{0}^{2}:\)
For \(m=0\) and \(\varepsilon _{0}^{(1,2)}=0,\) the latter beams have the peculiar property of conserving the same disturbance distribution, apart from the phase factor, across any plane parallel to the xy-plane in the direction of propagation: \(x=x_{0}+\delta _{0}^{(1)}s, y=y_{0}+\delta _{0}^{(2)}s, z=z_{0}+s.\) Graphical examples are given in [80].
Diffraction-free Bessel beams are reviewed in [3, 141] (see also [46, 47, 56, 130] and the references therein for classical accounts on propagation-invariant optical fields and Bessel modes).
3.7 Spiral beams
Two-dimensional solutions of the paraxial wave equation (3.26), that possess the propagation-invariant property
under rotation and rescaling \(X=\rho (s)\left( x\cos \theta (s)+y\sin \theta \left( s\right) \right)\), \(Y=\rho (s)\left( -x\sin \theta (s)+y\sin \theta \left( s\right) \right) ,\) were investigated in detail [8, 9, 115], and [121].
In Sect. 3.4, we have already analyzed the transition to a rotating frame of reference; see Eqs. (3.21)–(3.23). As a combined result, Eq. (3.26) by means of the substitution
can be transformed into the equation of motion for the isotropic planar harmonic oscillator in a perpendicular uniform magnetic field, namely:
(our transformation (3.27) can be thought of as its special case when \(\omega =0).\) An algorithmic derivation is provided in [80].
A straightforward use of Fock’s solutions (3.23) does not lead directly to a new family of spiral beams due to the cancelation of the crucial parameter \(\omega\) (see Sect. 3.5 in the Mathematica notebook [80]). For example, the solution
is verified by a direct substitution [80]. (A multi-parameter extension can be obtained by the action of Schrödinger’s group).
On the second thought, with the help of (3.35), we shall look for a spiral beam in the form:
Here, a familiar eigenfunction expansion [8, 9]:
in terms of Laguerre-Gaussian modes, must satisfy the auxiliary equation (3.36). In complex form, \(z=1+is, T=\arg z=\arctan s,\) and
Denoting for \(m\ge 0,\)
we obtain an important “eigenfunction identity”:
by a direct evaluation [80].
As a result, substituting the series (3.39) into Eq. (3.36), one gets
or, in view of the completeness of the Laguerre-Gaussian modes,
Nontrivial solutions of this equation and the corresponding spiral beams are analyzed in the original works [8, 9]. A multi-parameter extension can be obtained by the action of Schrödinger’s group.
3.8 “Smart” lens design
A lens can be used to focus a laser beam to a small spot, or to produce a beam of suitable diameter and phase structure for injection into a given optical device [12, 72, 74, 96, 144, 147]. The multi-parameter modes under consideration allow one to adapt a required lens design in paraxial optics to the given field configuration. For instance, in the co-dimensional 1D case, let us consider the Gaussian package (3.17) when \(n=0.\) We found in Sect. 3.3 that the focal point is given by
say for \(\alpha _{0}\ge 0.\) In this section, let us consider a lens-like medium with quadratic refractive index [74], as in Eq. (3.7), on (0, l) such that our solutions (3.8 )–(3.14) can be used on this interval and the continuity condition holds at \(s=0.\) For the region \(s\ge l,\) one can take the Gaussian package in (3.17), once again, but with \(s\rightarrow s-l\), \(\alpha _{0}\rightarrow \alpha (l),\) etc. due to Eqs. (3.9)–(3.14), which automatically implies the field continuity at \(s=l.\) Moreover, critical points of the intensity inside the lens occur when
Here, \(\alpha \left( s_{\text {min},\text {max}}\right) =0,\) thus providing a one-to-one correspondence with the minimum-uncertainty squeezed states in quantum mechanics [81, 88]. For the length of lens we choose: \(0\le s_{\text {min}}<l<s_{\text {max}}.\) Then, location of the beam focal point in the homogeneous medium, after passing through the lens, is given by
As a result, in view of the invariant [88],
one arrives at the following relation between two focal points,
(Here, the corresponding solutions (3.9)–(3.14) are evaluated at the terminal point of the lens, \(s=l.)\) Finally,
for the beam radii at the focal points before, \((x_{0},s_{0}),\) and after, \((x_{f},s_{f}),\) the lens, respectively. According to our analysis, location of the terminal focal point \((x_{f},s_{f})\) and the corresponding beam radius \(r_{f}\) both depend on the lens length, l, which can be adjusted for an “optimal control” of the beam propagation through this lens in a certain optical device. For instance, by (3.47) and (3.50),
which attains its minimum and maximum values, namely,
at the critical points \(l=s_{\text {max},\text {min}},\) respectively (cf. [88]). An important ratio,
defines the maximum possible compression (or superfocusing in the terminology of Refs. [39, 40]) of the beam inside of a (sufficiently long) lens.
A numerical example Visualization of the intensity and optical energy distribution generated by a sample lens, when \(\alpha _{0}=2\beta _{0}=2,\, s_{\text {min}}=1.33897,\, l=2.75, \,s_{\text {max}}=2.90977,\, x_{0}=x_{f}=0,\, s_{0}=-0.23529,\, s_{f}=2.9106,\;{\text {and}}\;r_{0}=0.242536,\, r_{f}=0.239104,\) is given in Fig. 3; see also our supplementary material [80] for more details.
3.9 Applications to quantum mechanics
A similar effect of the superfocusing of proton beam in a thin monocrystal film was discussed in [39, 40] as certain dynamical manipulations with the system of particles by transforming high concentration in the momentum space (collinearity) into the concentration in the coordinate space (focusing) (validity of the 2D harmonic crystal model had been confirmed by Monte Carlo computer experiments [40]). In the context of quantum mechanics, the corresponding solutions represent the minimum-uncertainty, or squeezed, states of harmonic oscillators that are explicitly given in [88]. Our sample lens from the previous section can be thought of as a codimension 1D model of Demkov’s microscope.
Among other quantum mechanical analogs, the minimum-uncertainty squeezed states for atoms and photons in a cavity, are reviewed in [88]; some of them were experimentally realized on cold trapped atoms [93]. It is worth noting that similar states can be identified for the motion of a quantum particle in a uniform magnetic field [49].
3.10 Extensions to nonlinear paraxial optics
For high-intensity beams, nonlinear medium effects should be taken into account in the theory of wave propagation. See [43, 61, 89, 98–100, 117, 137, 144, 146] and the references therein for extensions to nonlinear geometrical optics. A generalization of Lemma 1 for combination of certain nonlinear terms is discussed in [100] but search for solutions of nonlinear equations is much more complicated.
In the 1D linear case, where nonspreading Airy beams were introduced [20] (see also [125, 126]), the symmetry of the free Schrödinger equation can be used in order to obtain multi-parameter solutions (3.6). Although the corresponding 1D cubic nonlinear Schrödinger equation is no longer preserved under the expansion transformation (but has a similarity reduction to the second Painlevé equation [52, 53, 98, 127, 134]), the same symmetry holds for the quintic nonlinear Schrödinger equation, which is thus invariant under the action of this group. Here, the blow up, namely a singularity such that the wave amplitude tends to infinity in a finite time, occurs (see [99, 133, 137] and the references therein).
As is well known, a similar symmetry holds for the homogeneous 2D cubic nonlinear Schrödinger equation [89, 135] (in optics this symmetry is known as Talanov’s transformation [146]). This is another classical example of the blow up phenomenon. The stationary 2D waveguides in homogeneous quadratic Kerr media are unstable [89]. Under certain conditions, self-focusing of light beams occurs on a finite distance despite diffraction spreading. Moreover, for parabolic channels in a monocrystal film, the cubic nonlinearity may further enhance superfocusing of particle beams predicted in [39, 40]. The corresponding inhomogeneous medium effects deserve a detailed study. An extension to randomly varying media is also of interest (cf. [11, 120, 136]).
4 Computer algebra methods
For an automatic verification of the results presented in this paper, we used the computer algebra system Mathematica, and in some specific instances, the HolonomicFunctions package [76], written by the first-named author in the frame of his Ph.D. thesis [75].Footnote 3 (See also [79] and the references therein for applications of the HolonomicFunctions package to relativistic Coulomb integrals.)
The application of computer algebra in the context of the present paper comes in three different flavors: The first one employs Gröbner bases, the second one is based on the built-in simplification procedures of Mathematica, and the third one is related to the above-mentioned HolonomicFunctions package.
Gröbner bases were introduced in [29] and are a very useful tool for computations with polynomial ideals. For finding “nice” expressions for the solutions (2.4)–(2.9) of the Riccati-type system, one can consider the ideal generated by the (polynomial) Eqs. (2.41)–(2.46). Equivalence of expressions then corresponds to equality modulo the ideal. See [80] for more details.
Similarly, we discovered an “invariant” of the Ermakov-type system. Again using Eqs. (2.41)–(2.46) as input (but now with \(c_{0}=1\)) one can use Gröbner bases to find relations that are implied by the given equations. Searching for an equation that does not involve the parameters a, b, c, d, f, g yields the identity
which was missing in the original publications. It reveals that the differential equations in the Ermakov-type system are in fact dependent. In particular, Eq. (2.46) for \(\kappa ^{\prime }\) can be derived from the previous equations of this system.
To demonstrate the other two applications, recall the multi-parameter Airy modes B(x, s) given in Eq. (3.6). Thanks to the progress that computer algebra systems like Mathematica have been made during the past decades, particularly in dealing with special functions, it can be directly verified that B(x, s) satisfies the parabolic equation (3.1): one just inputs the expression given on the right-hand side of (3.6) and differentiates it symbolically. Then the command FullSimplify successfully simplifies the expression \(iB_{s}+B_{xx}\) to 0, see the corresponding section in the accompanying notebook [80].
The last approach achieves more and is a bit of an overhead if one only wanted to verify that B(x, s) satisfies the given differential equation. Namely, the HolonomicFunctions package computes the set of all differential equations that a given expression satisfies (more precisely: a finite basis of this, in general, infinite set). For the multi-parameter Airy modes, the software computes the following two differential equations:
where the polynomial coefficients \(p_{1}\) and \(p_{2}\) are given by
and where \(\alpha =\alpha (0)\) etc. Obviously, the parabolic equation \(iB_{s}+B_{xx}=0\) is just a simple linear combination of the above two equations. Thus, we again have proved that B(x, s) satisfies \(iB_{s} +B_{xx}=0\), but even more: the program has found this equation automatically, starting from the closed form of its solution as the sole input.
Similarly, the remaining formulas in this paper can be verified and/or derived. For the holonomic systems approach to work, some inputs have to be transformed into an appropriate format, e.g., the expression given by (3.8)–(3.14): holonomic functions are closed under addition, multiplication, and substitution of algebraic expressions. Since \(\sin (s)\) and \(\cos (s)\), which appear in the argument of the Hermite polynomials, are not algebraic, one may apply the transformation \(s\mapsto i\log (z)\) in order to turn the trigonometric functions into rational functions. More details and all other computations are contained in the accompanying Mathematica notebook [80].
5 Conclusion
This work is dedicated to a mathematical description of light propagation in turbid media and/or through optical systems that are subject to a natural noisy environment. To this end, we apply concepts of the Fresnel diffraction, the generalized lens transformation, see Lemma 1, and computer algebra tools [75–77] in order to analyze multi-parameter families of certain propagation-invariant laser beams in codimension 1D and 2D configurations that are important in paraxial optics and its applications. Independent proofs of these results are provided in the supplementary electronic material [80] along with a computer algebra verification of all related mathematical tools introduced in the original publications without sufficient details. In summary, the “missing” multi-parameter solutions of the paraxial wave equations, that are studied in this article, allow one to describe all main features of the special laser modes propagation in a variety of optical systems, in a consistent mathematical way, with the help of a computer algebra system. In numerical simulations, we have concentrated on results which are potentially of a practical and academic value, e.g., for software development and pedagogy.
Notes
From now on, we abbreviate \(\alpha _{0}=\alpha (0),\) etc for the sake of compactness.
The package can be downloaded from http://www.risc.jku.at/research/combinat/software/HolonomicFunctions/.
References
D. Abdollahpour, S. Suntsov, D.G. Papazoglou, S. Tzortzakis, Spatiotemporal Airy light bullets in the linear and nonlinear regimes. Phys. Rev. Lett. 105(25), 253901 (2010)
E.G. Abramochkin, unpublished manuscript (in Russian)
E.G. Abramochkin, T. Alieva, J.A. Rodrigo, Solutions of paraxial equations and families of Gaussian beams, in Mathematical Optics: Classical, Quantum, and Computational Methods, ed. by V. Lakshmianrayanan, M.L. Calvo, T. Alieva (CRC Press, Boca Raton, 2013), pp. 143–192
E.G. Abramochkin, E. Razueva, Product of three Airy beams. Opt. Lett. 36(19), 3732–3734 (2011)
E.G. Abramochkin, V.G. Volostnikov, Two-dimensional phase problem: differential approach. Opt. Commun. 74(3), 139–143 (1989)
E.G. Abramochkin, V.G. Volostnikov, Relationship between two-dimensional intensity and phase in a Fresnel diffraction zone. Opt. Commun. 74(3), 144–148 (1989)
E.G. Abramochkin, V.G. Volostnikov, Beam transformations and nontransformed beams. Opt. Commun. 83(1–2), 123–135 (1991)
E.G. Abramochkin, V.G. Volostnikov, Spiral light beams. Phys. Uspekhi 47(12), 1177–1203 (2004)
E.G. Abramochkin, V.G. Volostnikov, Modern Optics of Gaussian Beams (FizMatLit, Moscow, 2010). (in Russian)
G.P. Agrawal, A.K. Ghatak, C.L. Mehtav, Propagation of a partially coherent beam through selfoc fibers. Opt. Commun. 12(3), 333–337 (1974)
S.A. Akhmanov, Y.E. Dyakov, A.S. Chirkin, An Introduction to Statistical Radiophysics and Optics (Nauka, Moscow, 1981). (in Russian)
S.A. Akhmanov, S.Y. Nikitin, Physical Optics (Clarendon Press, Oxford, 1997)
C. Ament, P. Polynkin, J.V. Moloney, Supercontinuum generation with femtosecond self-healing Airy pulses. Phys. Rev. Lett. 107(24), 243901 (2011)
M.A. Bandres, Accelerating beams. Opt. Lett. 34(24), 3791–3793 (2009)
M.A. Bandres, J.C. Gultiérrez-Vega, Airy-Gauss beams and their transformation by paraxial optical systems. Opt. Express 15(25), 16719–16728 (2007)
M.A. Bandres, M. Guizar-Sicairos, Paraxial group. Opt. Lett. 34(1), 13–15 (2009)
M.A. Bandres, I. Kaminer, M. Mills, B.M. Rodriguez-Lara, E. Greenfield, M. Segev, D.N. Christodoulides, Accelerating optical beams. Opt. Photonic News 24(6), 30–37 (2013)
R. Bekenstein, M. Segev, Self-accelerating optical beams in highly nonlocal nonlinear media. Opt. Express 19(24), 23706–23715 (2011)
P.A. Bélanger, Packetlike solutions of the homogeneous-wave equation. J. Opt. Soc Am. A 1(7), 723–724 (1984)
M.V. Berry, N.L. Balazs, Nonspreading wave packets. Am. J. Phys. 47(2), 264–267 (1979)
I.M. Besieris, A.M. Shaarawi, R.W. Ziolkowski, Nondispersive accelerating wave packets. Am. J. Phys. 62(6), 519–521 (1994)
I.M. Besieris, A.M. Shaarawi, A note on an accelerating finite energy Airy beam. Opt. Lett. 32(16), 2447–2449 (2007)
I.M. Besieris, A.M. Shaarawi, Accelerating Airy beams with non-parabolic trajectories. Opt. Commun. 331, 235–238 (2014)
I. Bialynicki-Birula, Photon as a quantum particle. Acta Phys. Pol. B 37(3), 935–946 (2006)
I. Bialynicki-Birula, Z. Bialynicka-Birula, Canonical separation of angular momentum of light into its orbital and spin parts. J. Opt. 13(6), 064014 (2011)
C.P. Boyer, R.T. Sharp, P. Winternitz, Symmetry breaking interactions for the time dependent Schrödinger equation. J. Math. Phys. 17(8), 1439–1451 (1976)
M. Born, E. Wolf, Principles of Optics, 7th edn. (Pergamon Press, Oxford, 1999)
C. Brosseau, Polarization and coherence optics: historical perspective, status, and future directions, in Progress in Optics, ed. by E. Wolf (Elsevier, Amsterdam, 2009), pp. 149–208
B. Buchberger, Ein Algorithmus zum Auffinden der Basiselemente des Restklassenrings nach einem nulldimensionalen Polynomideal. PhD thesis, University of Innsbruck, Austria, 1965
R.-P. Chen, C.-F. Yin, X.-X. Chu, H. Wang, Effect of Kerr nonlinearity on an Airy beam. Phys. Rev. A 82, 043832 (2010)
R.-P. Chen, H.-P. Zheng, C.-Q. Dai, Wigner distribution function of an Airy beam. J. Opt. Soc. Am. A 28(6), 1307–1311 (2011)
A. Chong, W.H. Renninger, D.N. Christodoulides, F.W. Wise, Airy-Bessel wave packets as versatile linear light bullets. Nat. Photonics 4(2), 103–106 (2010)
R. Cordero-Soto, R.M. Lopez, E. Suazo, S.K. Suslov, Propagator of a charged particle with a spin in uniform magnetic and perpendicular electric fields. Lett. Math. Phys. 84(2–3), 159–178 (2008)
R. Cordero-Soto, S.K. Suslov, Time reversal for modified oscillators. Theor. Math. Phys. 162(3), 286–316 (2010)
R.T. Couto, Green’s functions for the wave, Helmholtz and Poisson equations in a two-dimensional boundless domain. Revista Brasileira de Ensino de Física 35(1), 1304 (2013)
Y.A. Danilov, G.I. Kuznetsov, Y.A. Smorodinsky, On the symmetry of classical and wave equations. Sov. J. Nucl. Phys. 32(6), 801–804 (1980)
J.A. Davis, M.J. Mitry, M.A. Bandres, D.M. Cottrell, Observation of accelerating parabolic beams. Opt. Express 16(17), 12866–12871 (2008)
J.A. Davis, M.J. Mitry, M.A. Bandres, I. Ruiz, K.P. McAuley, D.M. Cottrell, Generation of accelerating Airy and accelerating parabolic beams using phase-only patterns. Appl. Opt. 48(17), 3170–3176 (2009)
Y.N. Demkov, Channeling, superfocusing, and nuclear reactions. Phys. Atomic Nucl. 72(5), 779–785 (2009)
Y.N. Demkov, J.D. Meyer, A sub-atomic microscope, superfocusing in channeling and close encounter atomic and nuclear reactions. Eur. Phys. J. B 42, 361–365 (2004)
D.M. Deng, Propagation of Airy-Gaussian beams in a quadratic-index medium. Eur. Phys. J. D 65, 553–556 (2010)
D.M.R. Dennis, J.B. Götte, R.P. King, M.A. Morgan, M.A. Alonso, Paraxial and nonparaxial polynomial beams and the analytic approach to propagation. Opt. Lett. 36(22), 4452–4454 (2011)
A.S. Desyatnikov, D. Buccoliero, M.R. Dennis, Y.S. Kivshar, Suppression of collapse for spiraling elliptic solutions. Phys. Rev. Lett. 104, 053902 (2010)
I.H. Deutsch, J.C. Garrison, Paraxial quantum propagation. Phys. Rev. A 43(5), 2498–2513 (1991)
V.V. Dodonov, V.I. Man’ko, Invariants and correlated states of nonstationary quantum systems, in Invariants and the Evolution of Nonstationary Quantum Systems, Proceedings of Lebedev Physics Institute, vol. 183, pp. 71–181, Nauka, Moscow, 1987 (in Russian); English translation published by Nova Science, Commack, New York, 1989, pp. 103–261
J. Durnin, Exact solutions for nondiffracting beams I. The scalar theory. J. Opt. Soc. Am. A 4(4), 651–654 (1987)
J. Durnin, J.J. Miceli Jr, J.H. Eberly, Diffraction-free beams. Phys. Rev. Lett. 58(15), 1499–1501 (1987)
G. Eichmann, Quasi-geometric optics of media with inhomogeneous index of refraction. J. Opt. Soc. Am. 61(2), 161–168 (1971)
V. Fock, Bemerkung zur Quantelung des harmonischen Oszillators im Magnetfeld. Zs. für Phys. 47, 446–448 (1928). translated to English: A Comment on Quantization of the Harmonic Oscillator in a Magnetic Field, in Selected Works: Quantum Mechanics and Quantum Field Theory, ed. by L.D. Faddeev, L.A. Khalfin, I.V. Komarov (Chapman & Hall/CRC, Boca Raton, London, New York, Washington, DC, 2004), pp. 29–31
V.A. Fock, Electromagnetic Diffraction and Propagation Problems (Pergamon Press, London, 1965)
S. Fürhapter, A. Jesacher, S. Bernet, M. Ritsch-Marte, Spiral interferometry. Opt. Lett. 30(15), 1953–1955 (2005)
L. Gagnon, P. Winternitz, Lie symmetries of a generalised non-linear Schrödinger equation: II. Exact solutions. J. Phys. A Math. Gen. 22, 469–497 (1989)
J.A. Giannini, R.I. Joseph, The role of the second Painlevé transcendent in nonlinear optics. Phys. Lett. A 141(8), 417–419 (1989)
G. Gibson, J. Courtial, M.J. Padgett, M. Vasnetsov, V. Pas’ko, S.M. Barnett, S. Franke-Arnold, Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 12(22), 5448–5456 (2004)
A.M. Goncharenko, Gaussian Beams of Light (Nauka & Tekhnika, Minsk, 1977). (in Russian)
F. Gori, G. Guattari, C. Padovani, Bessel–Gauss beams. Opt. Commun. 64(6), 491–495 (1987)
D.M. Greenberg, Comment on “Nonspreading wave packets”. Am. J. Phys. 48(3), 256 (1980)
Y. Gu, G. Gbur, Scintillation of Airy beam arrays in atmospheric turbulence. Opt. Lett. 35, 3456–3458 (2010)
Y. Gu, Statistics of optical vortex wander on propagation through atmospheric turbulence. J. Opt. Soc. Am. A 30(4), 708–716 (2013)
G. Gbur, T.D. Visser, Coherence vortices in partially coherent beams. Opt. Commun. 222, 117–125 (2003)
A.V. Gurevich, Nonlinear Phenomena in the Ionosphere (Springer, Berlin, 1978)
J. Hamazaki, R. Morita, K. Chujo, Y. Kobayashi, S. Tanda, T. Omatsu, Optical-vortex laser ablation. Opt. Express 18(3), 2144–2151 (2010)
M.R. Hatzvi, Y.Y. Schechner, Three-dimensional optical transfer of rotating beams. Opt. Lett. 37, 32074 (2012)
H.A. Haus, J.L. Pan, Photon spin and the paraxial wave equation. Am. J. Phys. 61(9), 818–821 (1993)
J.D. Jackson, Classical Electrodynamics, 2nd edn. (Wiley, New York, 1975)
I. Kaminer, M. Segev, D.N. Christodoulides, Self-accelerating self-trapped optical beams. Phys. Rev. Lett. 106, 213903 (2011)
J. Kasparian, J.-P. Wolf, Laser beams take a curve. Science 324, 194–195 (2009)
C. Kharif, E. Pelinovsky, A. Slunyaev, Rogue Waves in the Ocean (Springer, Berlin, 2009)
A.P. Kiselev, Localized light waves: paraxial and exact solutions of the wave equation (a review). Opt. Spectrosc. 102(4), 603–622 (2007)
A.P. Kiselev, M.V. Perel, Highly localized solutions of the wave equation. J. Math. Phys. 41(4), 1934–1955 (2000)
A.P. Kiselev, A.B. Plachenov, P. Chamorro-Posada, Nonparaxial wave beams and packets with general astigmatism. Phys. Rev. A 85(4), 043835 (2012)
M. Kline, I.W. Kay, Electromagnetic Theory and Geometrical Optics (Interscience Publishers, New York, 1965)
H. Kogelnik, On the propagation of Gaussian beams of light through lenslike media including those with a loss or gain variation. Appl. Opt. 4(12), 1562–1569 (1965)
H. Kogelnik, T. Li, Laser beams and resonators. Appl. Opt. 5(10), 1550–1567 (1966)
C. Koutschan, Advanced applications of the holonomic systems approach. PhD thesis, Research Institute for Symbolic Computation (RISC), Johannes Kepler University, Linz, Austria, 2009
C. Koutschan, HolonomicFunctions (user’s guide), RISC Report Series, Johannes Kepler University, Linz, Austria, 2010; http://www.risc.jku.at/research/combinat/software/HolonomicFunctions/
C. Koutschan, Creative telescoping for holonomic functions, in Computer Algebra in Quantum Field Theory: Integration, Summation and Special Functions, ed. by C. Schneider, J. Blümlein Springer Series “Texts and Monographs in Symbolic Computation” (Springer, Wien, 2013), pp. 171–194
C. Koutschan, Mathematica notebook Koutschan.nb, http://hahn.la.asu.edu/~suslov/curres/index.htm; see also http://iopscience.iop.org/0953-4075/46/10/104007/media
C. Koutschan, P. Paule, S.K. Suslov, Relativistic Coulomb Integrals and Zeilbergers Holonomic Systems Approach II, in AADIOS 2012—Algebraic and Algorithmic Aspects of Differential and Integral Operators Session, ed. by M. Barkatou et al., Lecture Notes in Computer Sciences, vol. 8372 (Springer, 2014) pp. 135–145
C. Koutschan, E. Suazo, S.K. Suslov, Mathematica notebook MultiParameterModes.nb, supplementary electronic material to the article Fundamental Laser Modes in Paraxial Optics: From Computer Algebra and Simulations to Experimental Observation, http://www.koutschan.de/data/lasermodes/, 2015
C. Krattenthaler, S.I. Kryuchkov, A. Mahalov, S.K. Suslov, On the problem of electromagnetic-field quantization. Int. J. Theor. Phys. 52(12), 4445–4460 (2013); see also arXiv:1301.7328v2 [math-ph] 9 Apr 2013
Y.A. Kravtsov, Y.I. Orlov, Geometrical Optics of Inhomogeneous Media (Springer, Berlin, 1990)
S.G. Krivoshlykov, I.N. Sissakian, Optical beam and pulse propagation in inhomogeneous media. Application to multiple parabolic-index waveguides. Opt. Quantum Electron. 12, 463–475 (1980)
S.G. Krivoshlykov, N.I. Petrov, I.N. Sissakian, Spacial coherence of optical beams in longitudinally inhomogeneous media with quadratic refractive index profiles. Sov. J. Quantum Electron. 15(3), 330–338 (1985)
S.G. Krivoshlykov, N.I. Petrov, I.N. Sissakian, Correlated coherent states and propagation of arbitrary Gaussian beams in longitudinally inhomogeneous quadratic media exhibiting absorption or amplification. Sov. J. Quantum Electron. 16(7), 933–941 (1986)
S.G. Krivoshlykov, E.G. Sauter, Transformation of paraxial beams in arbitrary multimode parabolic-index fiber tapers by using a quantum-theoretical approach. Appl. Opt. 31(7), 2017–2024 (1992)
S.I. Kryuchkov, N. Lanfear, S.K. Suslov, The Pauli–Lubański vector, complex electrodynamics, and photon helicity. Phys. Scr. 90(7), 074065 (2015)
S.I. Kryuchkov, S.K. Suslov, J.M. Vega-Guzmán, The minimum-uncertainty squeezed states for atoms and photons in a cavity. J. Phys. B Atomic Mol. Opt. Phys. 46, 104007 (2013). (IOP Select and Highlight of 2013)
E.A. Kuznetsov, S.K. Turitsyn, Talanov transformations in self-focusing problems and instability of stationary waveguides. Phys. Lett. A 112(6–7), 273–275 (1985)
N. Lanfear, R.M. López, S.K. Suslov, Exact wave functions for generalized harmonic oscillators. J. Russ. Laser Res. 32(4), 352–361 (2011)
M. Lax, W.H. Louisell, W.B. McKnight, From Maxwell to paraxial wave optics. Phys. Rev. A 11(4), 1365–1370 (1975)
A. Lotti et al., Stationary nonlinear Airy beams. Phys. Rev. A 84, 021807(R) (2011)
D. Leibfried, R. Blatt, C. Monroe, D. Wineland, Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75(1), 281–324 (2003)
R.M. López, S.K. Suslov, J.M. Vega-Guzmán, Reconstracting the Schrödinger groups. Phys. Scr. 87(3), 038118 (2013)
R.M. López, S.K. Suslov, J.M. Vega-Guzmán, On a hidden symmetry of quantum harmonic oscillators. J. Differ. Equ. Appl. 19(4), 543–554 (2013)
R.K. Luneburg, Mathematical Theory of Optics (University of California Press, Berkeley, 1964)
A. Mahalov, E. Suazo, S.K. Suslov, Spiral laser beams in inhomogeneous media. Opt. Lett. 38(15), 2763–2766 (2013)
A. Mahalov, S.K. Suslov, An “Airy gun”: self-accelerating solutions of the time-dependent Schrödinger equation in vacuum. Phys. Lett. A 377, 33–38 (2012)
A. Mahalov, S.K. Suslov, Wigner function approach to oscillating solutions of the 1D-quintic nonlinear Schrödinger equation. J. Nonlinear Opt. Phys. Mater. 22(2), 1350013 (2013)
A. Mahalov, S.K. Suslov, Solution of paraxial wave equation for inhomogeneous media in linear and quadratic approximation. Proc. Am. Math. Soc. 143(2), 595–610 (2015)
A. Mair, A. Vaziri, G. Weihs, A. Zeilinger, Entanglement of the orbital angular momentum states of photons. Nature 412(19), 313–316 (2001)
M.E. Marhic, Oscillating Hermite-Gaussian wave functions of the harmonic oscillator. Lett. Nuovo Cim. 22(8), 376–378 (1978)
M.A.M. Marte, S. Stenholm, Paraxial light and atom optics: the Schrödinger equation and beyond. Phys. Rev. A 56(4), 2940–2953 (1997)
M. Meiler, R. Cordero-Soto, S.K. Suslov, Solution of the Cauchy problem for a time-dependent Schödinger equation. J. Math. Phys. 49, 072102 (2008)
W. Miller Jr, Symmetry and Separation of Variables, Encyclopedia of Mathematics and Its Applications, vol. 4 (Addison-Wesley Publishing Company, Reading, 1977)
G. Molina-Terriza, J.P. Torres, L. Torner, Twisted photons. Nat. Phys. 3(5), 305–310 (2007)
U. Niederer, The maximal kinematical invariance group of the free Schrödinger equations. Helv. Phys. Acta 45, 802–810 (1972)
U. Niederer, The maximal kinematical invariance group of the harmonic oscillator. Helv. Phys. Acta 46, 191–200 (1973)
A.F. Nikiforov, V.B. Uvarov, Special Functions of Mathematical Physics (Birkhäuser, Basel, 1988)
A.F. Nikiforov, S.K. Suslov, V.B. Uvarov, Classical Orthogonal Polynomials of a Discrete Variable (Springer, Berlin, 1991)
B. Øksendal, Stochastic Differential Equations (Springer, Berlin, 2000)
A.Y. Okulov, Angular momentum of photons and phase conjugation. J. Phys. B Atomic Mol. Opt. Phys. 41, 101001 (2008)
F.W.J. Olver, Airy and related functions, in NIST Handbook of Mathematical Functions, ed. by F.W.J. Olwer, D.M. Lozier, et al. (Cambridge University Press, Cambridge, 2010). see also: http://dlmf.nist.gov/9
X. Pang, G. Gbur, T.D. Visser, The Gouy phase of Airy beams. Opt. Lett. 36(13), 2492–2494 (2011)
R. Piestun, Y.Y. Schechner, J. Shamir, Propagation-invariant wave fields with finite energy. J. Opt. Soc. Am. A 17(2), 294–303 (2000)
P. Polynkin, M. Kolesik, J.V. Moloney, G.A. Siviloglou, D.N. Christodoulides, Curved plasma channel generation using ultraintense Airy beams. Science 324, 229–232 (2009)
S.A. Ponomarenko, G.P. Agrawal, Do solitonlike self-similar waves exist in nonlinear optical media? Phys. Rev. Lett. 97, 013901 (2006)
R. Pratesi, L. Ronchi, Generalized Gaussian beams in free space. J. Opt. Soc. Am. 67(9), 1274–1276 (1977)
A. Rudnick, D.M. Marom, Airy-soliton interactions in Kerr media. Opt. Express 19(25), 25570–25582 (2011)
S.M. Rytov, Y.A. Kravtsov, V.I. Tatarskii, Principles of Statistical Radiophysics: Wave Propagation Through Random Media (Springer, Berlin, 1989)
Y.Y. Schechner, R. Piestun, J. Shamir, Wave propagation with rotating intensity distributions. Phys. Rev. E 54(1), R50–R53 (1996)
U.T. Schwarz, M.A. Banderes, J.C. Gutiérrez-Vega, Observation of Ince–Gaussian modes in stable resonators. Opt. Lett. 29(16), 1870–1872 (2004)
A.E. Siegman, Hermite-Gaussian functions of complex argument as optical-beam eigenfunctions. J. Opt. Soc. Am. 63(9), 1093–1094 (1973)
A.E. Siegman, Lasers (Univ. Sci. Books, Mill Valey, 1986)
G.A. Siviloglou, D.N. Christodoulides, Accelerating finite energy Airy beams. Opt. Lett. 32(2), 979–981 (2007)
G.A. Siviloglou, J. Broky, A. Dogariu, D.N. Christodoulides, Observation of accelerating Airy beams. Phys. Rev. Lett. 99, 213901 (2007)
R. Smith, Giant waves. J. Fluid Mech. 77(3), 417–431 (1976)
W.J. Smith, Modern Optical Engineering: The Design of Optical Systems, 3rd edn. (McGraw-Hill, New York, 2000)
A. Sommerfeld, Partial Differential Equations in Physics (Academic Press, New York, 1949)
P. Sprange, B. Hafizi, Comment on nondiffracting beams. Phys. Rev. Lett. 66(6), 837 (1991)
S. Steinberg, Applications of the Lie algebraic formulas of Baker, partial differential equations. J. Differ. Equ. 26, 404–434 (1977)
E. Suazo, S.K. Suslov, Soliton-like solutions for nonlinear Schrödinger equation with variable quadratic Hamiltonians. J. Russ. Laser Res. 33(1), 63–82 (2012)
S.K. Suslov, On integrability of nonautonomous nonlinear Schrödinger equations. Proc. Am. Math. Soc. 140(9), 3067–3082 (2012)
M. Tajiri, Similarity reduction of the one and two dimensional nonlinear Schrödinger equations. J. Phys. Soc. Jpn. 52(2), 1908–1917 (1983)
V.I. Talanov, Focusing of light in cubic media. JETP Lett. 11, 199–201 (1970)
W. Tang, A. Mahalov, Stochastic Lagrangian dynamics for charged flows in the E−F regions of ionosphere. Phys. Plasmas 20, 032305 (2013)
T. Tao, A pseudoconformal compactification of the nonlinear Schrödinger equation and applications. N. Y. J. Math. 15, 265–282 (2009)
A.V. Timofeev, Geometrical optics and the diffraction phenomenon. Phys. Uspekhi 48(6), 609–613 (2005)
A. Torre, Gaussian modulated Ai- and Bi-based solutions of the 2D PWE: a comparison. Appl. Phys. B 99, 775–799 (2010)
A. Torre, Paraxial equation, Lie-algebra-based approach, in Mathematical Optics: Classical, Quantum, and Computational Methods, ed. by V. Lakshmianrayanan, M.L. Calvo, T. Alieva (CRC Press, Boca Raton, 2013), pp. 341–417
J. Turunen, A.T. Friberg, Propagation-invariant optical fields, in Progress in Optics, ed. by E. Wolf (Elsevier, Amsterdam, 2009), pp. 1–88
K. Unnikrishnan, A.R.P. Rau, Uniqueness of the Airy packet in quantum mechanics. Am. J. Phys. 64(8), 1034–1035 (1996)
L.A. Vainshtein, Electromagnetic Waves, 2nd edn. (Radio i Svyaz’, Moscow, 1988). (in Russian)
M.B. Vinogradova, O.V. Rudenko, A.P. Sukhorukov, Theory of Waves, 2nd edn. (Nauka, Moscow, 1990). (in Russian)
V.S. Vladimirov, Equations of Mathematical Physics (Marcel Dekker, New York, 1971)
S.N. Vlasov, V.I. Talanov, The parabolic equation in the theory of wave propagation. Radiophys. Quantum Electron. 38(1–2), 1–12 (1995)
A. Walther, The Ray and Wave Theory of Lenses (Cambridge University Press, Cambridge, 1995)
E.M. Wright, J.C. Garrison, Path-integral derivation of the complex ABCD Huygens integral. J. Opt. Soc. Am. A 4(9), 1751–1755 (1987)
A. Wünsche, Coherence vortices in partially coherent beams. J. Opt. Soc. Am. A 6(9), 1320–1329 (1989)
A.M. Yao, M.J. Padgett, Orbital angular momentum: origins, behavior and applications. Adv. Opt. Photonics 3(2), 161–204 (2011)
A. Yariv, Quantum Electronics (Wiley, New York, 1988)
A. Yariv, P. Yeh, Photonics: Optical Electronics in Modern Communications, 6th edn. (Oxford University Press, Oxford, 2007)
Acknowledgments
This research was partially carried out during our participation in the Summer School on “Combinatorics, Geometry and Physics” at the Erwin Schrödinger International Institute for Mathematical Physics (ESI), University of Vienna, in June 2014. We wish to express our gratitude to Christian Krattenthaler for his hospitality. The first-named author was supported by the Austrian Science Fund (FWF): W1214, the second-named author by the Simons Foundation Grant #316295 and by the National Science Foundation Grant DMS-1440664, and the third-named author by the AFOSR Grant FA9550-11-1-0220. We are grateful to Eugeny G. Abramochkin, Sergey I. Kryuchkov, Vladimir I. Man'ko, and Peter Paule for valuable comments and to Miguel A. Bandres for kindly pointing out the reference [16] to our attention. Suggestions from the referees are much appreciated. Last but not least, we would like to thank Aleksei P. Kiselev for communicating the interesting articles [69–71].
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix 1: From Maxwell to paraxial wave
We follow [9] with somewhat different details. In dielectrics (no free current, no free charge, isotropic, homogeneous, material linear), the Maxwell equations for the complex electric \({\varvec{E}}\) and magnetic \({\varvec{H}}\) fields for a monochromatic wave varying as \({\text{e}}^{-i\omega t}\) are given by
where \(\varepsilon\) is the permittivity and \(\mu\) is the permeability of the material (see, for example, [12, 91, 143, 144]). Let us consider a “polarized” wave of the form,
where \(\left\{ {\varvec{e}}_{x},{\varvec{e}}_{y},{\varvec{e}} _{z}\right\}\) are orthonormal vectors in \(\left. {\mathbb {R}} \right. ^{3}.\) From the first Equation (5.1) one gets:
and the second Equation (5.1) is automatically satisfied. In addition, from the second Equation (5.2):
If \(g\equiv 0,\) then \(f_{x}=0\) and the only transversal solution is a plane wave, \({\varvec{E}}={\text{e}}^{ikz}{\varvec{e}}_{x},\) up to a constant multiple (cf. [91]).
In a similar fashion, from the first Equation (5.2) and (5.4) we obtain:
In view of (5.5), the latter equation can be simplified to
Finally, under the imposed conditions \(\left| f_{zz}\right| \ll 2\left| kf_{z}\right|\) and \(\left| g_{zz}\right| \ll 2\left| kg_{z}\right| ,\) we arrive to the paraxial wave equations,
for the transversal and longitudinal components, \(F=\left\{ f,g\right\} ,\) of the complex electric field, respectively. [The corresponding magnetic field can be evaluated by (5.4).] Once again, these components are related by (5.5), which implies that
and, integrating by parts,
provided that \(\left| k\right| \gg 1.\) In paraxial approximation, it is a custom to write
for the small longitudinal component of electric field that automatically satisfies (5.7). More details can be found in [9, 91]. A general solution is a superposition of two waves of the form (5.3).
Note The paraxial wave equations (5.7) for transversal and longitudinal components, \(F=\left\{ f(x,y,z),g(x,y,z)\right\} ,\) can be solved by the Fresnel integral,
subject to proper “initial” data, \(F_{0}=\left\{ f_{0}(x,y),g_{0}(x,y)\right\} ,\) which are related as follows,
in view of “divergence” condition (5.5). [When \(k\gg 1,\) one formally gets (5.9).]
In fact, Eq. (5.11) is the 2D inhomogeneous Helmholtz equation [129, 145]:
which can be solved exactly provided that function \(f_{0}(x,y)\) is known. Under the Sommerfeld radiation condition,
uniformly in \({\varvec{e}}\), \(\left| {\varvec{e}}\right| =1,\) one gets [35, 145]:
where \(H_{0}^{(1)}(z)\) is a Hankel function [109].
Appendix 2: From Maxwell to nonlinear paraxial optics
In a more general case (of a weakly inhomogeneous linear or nonlinear medium with a complex-valued dielectric permittivity \(\varepsilon ;\) see, for example, Refs. [50] and [143] for more details), one can look for solutions of Eqs. (5.1), (5.2) as a superposition,
of two “polarized” waves:
where f, g, h, l, and k are some complex-valued functions. In a similar fashion,
and
where, by definition,
Here, it is convenient to rewrite the last equation (5.2) as a sum of two equations:
We did not impose any conditions yet and Eqs. (5.15)–(5.20) are equivalent to the original Maxwell system (5.1)–(5.2) under consideration. For paraxial approximation, we may choose \(k_{zz}=0,\) namely, \(k(z)=kz,\) where k is a constant.
Let us first consider linear and nonlinear codimension 1D cases. When \(h=l=f_{y} =g_{y}=\varepsilon _{y}=0,\) one can simplify to
From the last equation,
Thus Eqs. (5.21) and (5.22) can be thought of as certain integro-differential equations for complex-valued functions f and g, respectively. Integrating by parts,
For large |k|, it is also a custom to assume that \(\left| f_{zz} \right| \ll 2\left| kf_{z}\right| ,\) \(\left| f_{zz}\right| \ll 2\left| kf_{z}\right| ,\) and \(|g|\ll |f|.\) As a result, one may concentrate on the study of scalar inhomogeneous paraxial wave equation of the form:
In a weakly inhomogeneous nonlinear medium, we expand the (complex-valued) permittivity \(\varepsilon ,\)
and neglect the higher order terms. In this approximation,
and one arrives at a form of the paraxial wave equation (2.1) (or its nonlinear versions).
The corresponding linear and nonlinear codimension 2D cases, when one can concentrate on a certain dominant component of electric field once again, are similar. Further details are left to the reader.
Rights and permissions
About this article
Cite this article
Koutschan, C., Suazo, E. & Suslov, S.K. Fundamental laser modes in paraxial optics: from computer algebra and simulations to experimental observation. Appl. Phys. B 121, 315–336 (2015). https://doi.org/10.1007/s00340-015-6231-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00340-015-6231-9