1 Introduction

The measurement of third-order nonlinear refractive indices is important to characterize materials with potential for photonic applications [1]. For this reason, advances in instrumentation and development of new methods for this area are sought. Despite all recent progress, there are still great challenges to be overcome due to the complexity of nonlinear processes, which need to be explored with different techniques, laser regimes, theoretical models and so on [2–6]; for instance, different nonlinear mechanisms can simultaneously contribute to the effective nonlinear signal and their discrimination may be difficult [7]. This partially explains why different nonlinearities values are found in the literature for the same material; for instance, Z-scan [8] and third-harmonic generation result to different nonlinear refractive indices in organic solvents [9]. Currently, even the most widespread material used as a nonlinear reference, fused silica, presents values in the literature that can differ by a factor of three at the same wavelength [10]. In order to have a better insight on the origin of the nonlinearity, the sign and time response can be investigated, as well as the tensorial nature of the nonlinear susceptibility because, depending on the nature of the nonlinearity and on the laser polarization, different nonlinear processes can be excited [7, 11].

There are several methods for measuring optical nonlinearities, and among them, the Z-scan technique based on the Kerr lens effect [8] became very popular due to its simplicity, precision, ability to measure nonlinear refraction (magnitude and sign) and nonlinear absorption with a single laser beam. However, it still has problems because the Kerr lens effect depends on the laser beam profile, sample surface quality and also on the presence of nonlinear effects with different origins that contribute to the single-beam Z-scan raw signal.

An interesting effect related to the third-order nonlinear refraction in isotropic media is the nonlinear rotation of an elliptically polarized laser beam [11]. Recently, we proposed a new method for measuring such nonlinear ellipse rotation (NER) with high precision by means of a phase-sensitive method [12]. The use of this technique is very interesting because the NER signal depends only on the third-order nonlinear susceptibility component, χ 1221.

The present work reports an advance to the NER technique for the measurement of refractive nonlinearities by applying it to the thick sample condition by using a short focus lens. In this case, smaller regions in the sample can be probed and so, better spatial resolution of the nonlinearity can be achieved. Furthermore, there is also an increase in the signal amplitude due to the maximization of the laser interaction region (entire Rayleigh range). In this approach, it is possible to simultaneously measure more than one nonlinear material in a single run, with better signal strength for a given laser irradiance; for instance, it is possible to stack one or more samples on top of a well known material that provides a reference signal. This single-beam measurement permits direct magnitude comparison and better signal-to-noise ratio since both samples are probed under the same laser conditions. Similar to the dual-arm Z-scan technique [4], this scheme allows much better comparison between the nonlinearities of two samples. Furthermore, due to the similar open-aperture configuration used in Z-scan, this method is less sensitive to beam transverse mode quality and sample surface quality.

In order to demonstrate the usefulness of this self-referenced NER method, we have measured several commercial optical glasses that are usually employed to make optical components and devices. It is important to know the magnitude of the refractive nonlinearity in such materials since they can be used with high-intense pulsed laser and, in this case, self-phase modulation, self-focusing, nonlinear polarization change and other nonlinear effects can perturb the laser beam propagation in optical devices. Moreover, it is important to characterize a large number of material’s nonlinearities using the same laser condition to test theoretical models and make comparison with values obtained with other methods.

2 Materials and methods

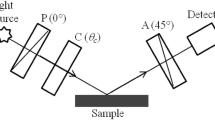
The experimental setup used for NER measurements, similar to that used in the open-aperture Z-scan technique [8], is shown schematically in Fig. 1. We employed pulses at λ = 775 nm with 150-fs pulse duration produced by a commercial Ti:sapphire chirped-pulsed-amplified system (CPA 2001, Clark MXR) at a 1 kHz repetition rate.

Fig. 1
figure 1

Schematic diagram of nonlinear ellipse rotation setup using a dual-phase lock-in

Full size image

A broadband zero-order quarter-wave plate is used to convert linear to elliptical polarization, and a short focal length lens focuses the laser beam into the sample, which translates through the focal position as in the Z-scan technique. In the tight focus condition, the NER occurs only at the Rayleigh length, and thus, two separated materials can be distinguished. Using a rotating analyzer and a dual-phase lock-in, one can determine the rotation (phase) with high accuracy and then the sample’s nonlinearity [12].

In order to demonstrate the method, we carried out two distinct experiments. In the first, we tested the transition from thin to thick sample condition by using silica with different thicknesses, namely 160, 250, 650 μm, 1.225 and 1.860 mm. In the second experiment, we measured several optical glasses stacked on a silica sample. We selected a large number of Schott glasses used to make optical components such as BK7, K10, LLF1, SK11, LLF6, F2, F14 and SF6, each one with a thickness of about 1 mm. Table 1 shows the thicknesses and other linear optical properties of these glasses. Predicted nonlinear refractive indices, n 2, were calculated with an empirical model [13, 14] that uses the linear index of refraction, n e (at λ = 546.1 nm), and its Abbe number, v e , according to:

Table 1 Thicknesses, refractive indices and Abbe numbers of the samples investigated
Full size table
$$n_{2} \left( {{\text{m}}^{ 2} / {\text{W}}} \right) = \frac{{2.85 \times 10^{ - 18} \left( {n_{e} - 1} \right)\left( {n_{e}^{2} + 2} \right)^{2} }}{{n_{e} v_{e} \left[ {1.517 + \frac{{\left( {n_{e}^{2} + 2} \right)\left( {n_{e} + 1} \right)}}{{6n_{e} }}v_{e} } \right]^{1/2} }}.$$
(1)

This expression leads to an approximate n 2 value which can be used to find the trends of the nonlinearities with the linear optical parameters of the glasses. Table 1 also shows the results predicted for the selected optical glasses, whose linear optical properties were obtained from the Schott glasses catalog [15].

Theoretical details of the NER method can be found in [12]. For a thin sample, assuming that no nonlinear absorption is present, the ellipse rotation in the plane wave approximation is given by:

$$\varTheta = \frac{1}{2}\left( {k\Delta nL} \right) = \frac{\omega }{c}\left( {\frac{\theta }{{1 + \theta^{2} }}} \right)\left[ {\frac{B}{{4n_{0}^{2} \varepsilon_{0} c}}} \right]LI,$$
(2)

where θ = tan ϕ is the ellipticity of the beam (ϕ is the angle between the polarization plane of the incident laser beam and the quarter-wave plate fast axis), B is the third-order nonlinear susceptibility (B = 6χ 1221), L is the sample length, ε 0 is the vacuum permittivity, ω is the laser frequency, c is the speed of light, n 0 is the linear refractive index, and I is the laser irradiance. The quarter-wave plate is used to control the polarization state of the laser beam; for instance, ϕ set at 0° and 45° gives linear and circular polarizations, respectively. For laser beams with Gaussian transversal beam profiles, the laser irradiance must be divided by two (I(z = 0) = I/2) [16] and in this case, the rotation angle is:

$$\alpha = \frac{\omega }{2c}\left( {\frac{{{ \sin }\,2\phi }}{2}} \right)\left[ {\frac{B}{{4n_{0}^{2} \varepsilon_{0} c}}} \right]\quad LI = \frac{\omega }{c}\left( {\frac{{{ \sin }\,2\phi }}{2}} \right)\frac{{n_{2} }}{3}LI.$$
(3)

For a thin sample, the rotation observed is proportional to the laser irradiance at each z-position, and since the irradiance is inversely proportional to the square of the beam waist, the rotation angle will depend on z according to:

$$\alpha \left( z \right) = \frac{{\alpha_{ \hbox{max} } }}{{\left( {1 + \left( {\frac{z}{{z_{\text{R}} }}} \right)^{2} } \right)}} = \frac{{\frac{\omega }{c}\left( {\frac{{{ \sin }\,2\phi }}{6}} \right)n_{2} {\text{LI}}}}{{\left( {1 + \left( {\frac{z}{{z_{\text{R}} }}} \right)^{2} } \right)}},$$
(4)

where α max is the maximum phase (angle) achieved for a given ellipticity of the laser beam, defined by ϕ, and z R is the Rayleigh range. This gives a Lorentzian curve as that obtained in typical absorptive processes.

Considering that the NER measurement is very similar to two-photon absorption (2PA) using the Z-scan technique, we propose an equation for NER in thick sample condition similar to that used for the thick sample Z-scan method [17]. The ellipse rotation angle as a function of sample position will be:

$$\alpha \left( z \right) = \frac{\omega }{c}\left( {\frac{{{ \sin }\,2\phi }}{6}} \right)n_{2} \left( {n_{0} z_{\text{R}} } \right)I\left[ {{ \tan }^{ - 1} \left( {z_{b} /z_{\text{R}} } \right) - { \tan }^{ - 1} \left( {z_{a} /z_{\text{R}} } \right)} \right]$$
(5)

where z b  = z + L/(2n 0) and z a  = z − L/(2n 0). In this case, the effective sample thickness is the Rayleigh length (n 0 z R). As can be noticed, the absolute value of the term in brackets increases as function of the sample geometrical thickness L until reaching a saturation for L ≫ n 0 z R. This leads to a plateau in the NER curve as function of z.

The NER measurement is performed with pulsed lasers, and so, it is necessary to consider the time-averaged ellipse rotation, which for a temporal Gaussian pulse and a fast nonlinearity is <α max> = α max/√2. It is also important to point out that in NER measured with a rotating analyzer, the angle determined by the lock-in amplifier is twice the real angle due to Malus’s law (α = α lock-in/2). However, for sandwiched samples that are measured simultaneously at same laser conditions, only the relative rotation value matters. Finally, taking into account these corrections, we obtain equations for the NER signal as:

$$\left\langle {\alpha \left( z \right)} \right\rangle_{\text{lock - in}} = \frac{{\frac{\omega }{c}\left( {\frac{{{ \sin }\,2\phi }}{3\sqrt 2 }} \right)n_{2} LI}}{{\left( {1 + \left( {\frac{z}{{z_{\text{R}} }}} \right)^{2} } \right)}},$$
(6)

for thin sample and:

$$\left\langle {\alpha \left( z \right)} \right\rangle_{\text{lock-in}} = \frac{\omega }{c}\left( {\frac{{{ \sin }\,2\phi }}{3\sqrt 2 }} \right)n_{2} n_{0} z_{\text{R}} I\left[ {{ \tan }^{ - 1} \left( {z_{b} /z_{\text{R}} } \right) - { \tan }^{ - 1} \left( {z_{a} /z_{\text{R}} } \right)} \right],$$
(7)

for the thick sample. In fact, Eq. (7) is also valid for thin sample. Figure 2 shows the behavior of Eq. (7) for samples of different thicknesses. In the limit of thin sample (L ≪ n 0 z R), Eq. (7) reduces to Eq. (6), but for very thick samples (L ≫ n 0 z R), an analysis at z = 0 indicates a saturation by a factor of π(n 0 z R)/L when the theories for thick and thin samples are compared. Figure 2b shows that the saturation is well developed for L/(n 0 z R) > 20.

Fig. 2
figure 2

a Theoretical NER signal given by Eq. (7) for silica samples as function of z-position with different L/(n 0 z R), and b the maximum rotation as function of L/(n 0 z R) at z = 0, for laser parameters: I = 600 GW/cm2, ϕ = 22.5°, z R = 0.23 mm, λ = 775 nm, n 0 = 1.45 and n 2 = 2.5 × 10−20 m2/W [10]

Full size image

3 Results and discussion

In order to work with the highest signal-to-noise ratio, all measurements were carried out with a fixed beam ellipticity obtained with the wave plate set to an angle ϕ = 22.5° [12]. Although the NER signal is not maximum in this condition, it presents lower noise that allows a better comparison of the nonlinearities.

In the first experiment, we tested the empirical model proposed for thin and thick samples. Here, we kept the same laser beam configuration (f = 8 cm, I 0 ~ 600 GW/cm2) and used samples with different thicknesses. The results of Fig. 3 can be fitted by Eq. (7) regardless of the sample thickness, providing a n 2 value of (2.5 ± 0.5) × 10−20 m2/W (B = (3.7 ± 0.7) × 10−22 m2/V2), which agrees with that reported in [10]. The experimental errors (~20 %) are originated from uncertainty in the peak value of the on-axis irradiance at the focus, which is related to the beam waist, pulse width and energy calibration. Furthermore, it is possible to determine the Rayleigh range (z R = 0.23 mm) and, consequently, the beam waist at the focal point (w 0 ~ 7.5 μm). In the results of Fig. 3, it is not possible to observe the NER signal saturation, characterized by the presence of a plateau, even for the thickest sample used (L = 1.86 mm, L/(n 0 z R) ~ 5.6).

Fig. 3
figure 3

Rotation signal in silica with different thicknesses as a function of the sample z-position. The lines are the theoretical fitting provided by Eq. (7)

Full size image

Once we have demonstrated that Eq. (7) is valid for thin and thick samples, we replaced the 8-cm lens by another with a shorter focal length (f = 3 cm) in order to decrease the Rayleigh range and approach the saturation regime (L ≫ n 0 z R). In this second set of experiments, we stacked two samples for each measurement, where one of them was a silica reference sample with 1.225 mm. In this case, we can use Eq. (7) for each sample by taking into account the focal plane position, and the corrected z a and z b, which must be shifted in accordance with the position of each sample. If the Rayleigh length is completely contained inside a particular sample, the NER signal is due to that sample only. For regions near the interface (z = 0) between the two samples, the contributions of each sample have to be considered. In this way, it is possible to find the fitting curve for staked samples, provided that we use the correct values of linear and nonlinear refractive indices, sample thicknesses (glasses and silica), sample and beam position, Rayleigh range and laser irradiance.

Through the fitting procedure, it is also possible to determine the laser beam parameter z R (z R = 0.03 mm) and, consequently, the beam waist at the focal point (w 0 ~ 2.7 μm). Besides, using the value of n 2 for silica, the laser irradiance can be determined as I 0 ≈ 400 GW/cm2. Figure 4 shows that the silica signal was the same in all measurements (~0.02 rad), and the other samples presented higher values. One can see clear plateaus in all samples, indicating that z R used here was short enough in comparison to the sample’s thickness (~1 mm, L/(n 0 z R) ~ 23). In general, the expected n 2 of all samples was very close to those calculated by Eq. (1) and also found in the literature [18, 19]. In addition, even using a simple setup and moderate laser irradiance, we were able to obtain reasonable signal-to-noise ratio. In this work, we highlight how to deal with thin and thick samples and not with high sensitivity as the beam deflection method [6] did recently.

Fig. 4
figure 4

NER signal measured as a function of sample z-position for different stacked samples. The silica sample gives the smaller plateau which can be used as a reference

Full size image

Roughly speaking, the nonlinearity of an unknown sample can be easily determined relative to the reference by directly comparing the level of the two plateaus that are clearly observed in the case of thick samples. However, in this simple method, small discrepancy can occur because the influence of the linear index of refraction of each sample is not taken into account. Furthermore, although the nonlinearities errors are quite high (~20 %) due to uncertainty in the peak laser irradiance determination, the n2 ratios to the reference material present lower uncertainties due to the high stability of NER signal when wave plate is set to an angle ϕ = 22.5° [12], but to be conservative, we also considered an uncertainty of ~20 % in the experimental n 2 ratios.

4 Conclusions

We have proposed an extension of the nonlinear ellipse rotation method using thick samples. The technique measures more than one sample in a single scan due to the ability of a complete discrimination of two samples. Using a known reference sample allows finding the refractive nonlinearity of other sample very quickly. We demonstrated that the NER technique at the tightly focused laser beam condition has great potential for studying third-order nonlinear refractive properties due to simplicity, low noise, high sensitivity and high precision. The nonlinearities of several optical materials were experimentally determined by this new NER method whose values are in agreement with those determined by a simple empirical equation and also found in the literature. Other applications such as nonlinear microscopy also can be potentially beneficed in the future with this work.