1 Introduction

Because of its many intriguing applications in the field of optical switching [1], logic, and signal processing [2–10], optical bistability has been the subject of intense research in various metal-based nanostructures, such as periodically nanostructured metal films, subwavelength metallic gratings [3], metal nanoparticle dimer [4], metal gap waveguides nanocavities [5, 6], metal–nonlinear dielectric multilayer structure [7, 8], metal nanoantenna involving Kerr nonlinear [9], and a planar metamaterial with broken structural symmetry on a nonlinear substrate [10]. The bistable optical response in these nanostructures commonly occurs under a relatively strong light illumination or by assisting with some large nonlinearity. Very luckily, metal–semiconductor hybrid nanostructures, which are expected to overcome those weaknesses in metal nanostructures, have been synthesized and provided a new way to explore the physical mechanism of optical bistability via the interaction between excitons in semiconductors and plasmons in metal nanostructures.

The exciton–plasmon interaction can significantly modify the optical properties of metal–semiconductor hybrid nanosystems, such as nonlinear Fano effect [11], coherent molecular resonances [12], electromagnetically induced transparency [13], energy transfer [14, 15], slow light effect [16, 17], superradiance [18], enhanced third-order nonlinear optical response [19], intensity-dependent enhancement of saturable absorption [20], enhancement of the second-harmonic generation [21], strongly modified four-wave mixing, and four-wave parametric amplification [22, 23]. To date, some inspiring results around optical bistability have been achieved, showing that an optical bistability regime occurs as the coupling between semiconductor quantum dot (SQD) and metal nanoparticle (MNP) becomes stronger by increasing the sizes of both SQD and MNP [24]. Then, Malyshev et al. [25] reported that a coupled SQD–MNP nanosystem could manifest bistability by measuring optical hysteresis of the Rayleigh scattering. Malyshev also derived the analytical bistability condition and the exact steady-state solution of the Bloch equations at the absolute bistability threshold in the similar system [26]. Recently, Knoester et al. [27] explored the switching times from the lower stable branch to the upper stable one. In our previous work, we revealed the bistable properties in hybrid SQD–MNP nanosystems at the position of Rayleigh resonance [28]. In other words, we only discussed optical bistable response in the case of the pump and probe fields with the same frequencies. Similar behaviors have also been reported in these literatures [24–26]. However, in hybrid SQD–MNP nanosystems, optical bistability assigned to three-photon effect has not been studied yet.

In this work, we present a scheme of a bistable nanodevice based on a coupled SQD–MNP nanosystem in the presence of the pump and probe fields with different frequencies. Detailed analysis shows that optical bistability can easily be achieved in such a nanosystem via exciton–plasmon interaction, and the bistability thresholds and the bistability region are highly sensitive to the structural parameters and excitation conditions of the hybrid system. Furthermore, we find that the bistable effect can be turned on or off by switching the polarization direction of the pump field. We also reveal the bistable properties of nonlinear absorption/refraction response arising from three-photon effect.

2 Model and theory

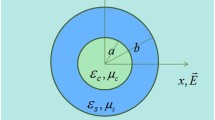
We consider such a system consisting of a spherical SQD with radius r and a spherical MNP with radius R, interacting with a strong pump field with amplitude E pu and frequency ω pu, and a weak probe field with amplitude E pr and frequency ω pr (E pu ≫ E pr). The MNP is attached to a sharp optical fiber tip. An atomic force microscope (AFM) can be used to probe the tip and stabilize its distance [29]. The surface-to-surface distance between two nanoparticles is denoted as d, as illustrated in Fig. 1. The Hamiltonian of the SQD in a rotating frame at the pump field frequency ω pu is expressed as

$$ H = \hbar \varDelta \sigma_{z} - \mu \left( {\tilde{E}_{\text{SQD}} \sigma_{01} + \tilde{E}_{\text{SQD}}^{ * } \sigma_{10} } \right). $$
(1)

where Δ = ω 10 − ω pu refers to the frequency difference between the exciton and the pump field, ω 10 is the frequency of exciton. σ 01 = |0><1| and σ 10 = |1><0| refer, respectively, to the creation and annihilation operators for an exciton, and σ z = (|1><1| − |0><0|)/2. µ is the interband dipole matrix element. Ẽ SQD is the total optical field felted by the SQD. Ẽ SQD = E/ε eff + S α P MNP /[ε 0 ε eff (d + r + R)3] with E = E pu + E pre−iδt, and ε eff = (2ε 0 + ε s)/(3ε 0) [30, 31], where δ = ω pr − ω pu is the detuning of the probe field from the pump field, and S α = 2 (−1) as the applied field is parallel (perpendicular) to the major axis of the nanosystem. ε 0 and ε s are the dielectric constants of the free space and the SQD, respectively. The dipole moment P MNP = α MNP Ẽ MNP comes from the charge induced on the surface of the MNP with α MNP = ε 0 R 3(ε m  − ε 0)/(2ε 0 + ε m ) and Ẽ MNP = E + S α P SQD /[ε 0(d + r + R)3] [32], and ε m is the dielectric constant of the MNP [33]. P SQD = µσ 10 is the dipole moment of the SQD [34]. In terms of the Heisenberg equation of motion, we have the temporal evolutions of the exciton as follows

$$ \dot{\sigma }_{10} = - \left( {\varGamma_{2} + i\varDelta } \right)\sigma_{10} - 2i\mu \tilde{E}_{\text{SQD}} \sigma_{z} /\hbar , $$
(2)
$$ \dot{\sigma }_{z} = - \left( {\sigma_{z} + 1/2} \right)\varGamma_{1} + 2\text{Im} \left( {\mu \sigma_{10} \tilde{E}_{\text{SQD}}^{ * } } \right)/\hbar . $$
(3)

where Γ 1 is the exciton relaxation rate and Γ 2 is the exciton dephasing rate. Ẽ SQD = f(E pu + E pre−iδt) + Gµσ 10 with f = 1/ε eff +S α α MNP/[ε 0 ε eff(d + r+R)3] and G = S 2 α α MNP/[ε 20 ε eff(d + r+R)6]. In order to solve Eqs. (2) and (3), we make the following ansatz [34]

$$ \sigma_{10} (t) = \sigma_{10}^{(0)} \left( {\omega_{pu} } \right) + \sigma_{10}^{(1)} \left( {\omega_{pu} + \delta } \right){\text{e}}^{ - i\delta t} + \sigma_{10}^{( - 1)} \left( {\omega_{\text{pu}} - \delta } \right){\text{e}}^{i\delta t} , $$
(4)
$$ \sigma_{z} (t) = \sigma_{z}^{(0)} \left( {\omega_{\text{pu}} } \right) + \sigma_{z}^{(1)} \left( {\omega_{pu} + \delta } \right){\text{e}}^{ - i\delta t} + \sigma_{z}^{( - 1)} \left( {\omega_{\text{pu}} - \delta } \right){\text{e}}^{i\delta t} . $$
(5)
Fig. 1
figure 1

a Schematic illustration and b energy-level diagram of a hybrid nanosystem composed of a semiconductor quantum dot and a metal nanoparticle in the simultaneous presence of a strong pump field E pu and a weak probe field E pr. The SQD is a two-level system consisting of the ground state |0> and the first excited state |1>

Full size image

Upon substituting Eqs. (4) and (5) to Eqs. (2) and (3) and working to the lowest order in E pr, but to all orders in E pu, the linear and nonlinear optical susceptibilities in the steady state are given by

$$ \begin{aligned} \chi_{\text{eff}}^{(1)} = & \frac{{\mu \sigma_{10}^{(1)} }}{{\varepsilon_{0} E_{\text{pr}} }} \\ = & \frac{{2f\mu^{2} \sigma_{z}^{(0)} }}{{\varepsilon_{0} \hbar \varGamma_{2} \left( {\delta_{\text{pr}} - \varDelta_{\text{pu}} - 2G_{\text{pu}} \sigma_{z}^{(0)} + i} \right)}}\left[ {1 - 2f^{2} \varOmega_{\text{pu}}^{2} \cdot \frac{{\left( {i - \varDelta_{\text{pu}} } \right)\left( {2i + \delta_{\text{pr}} } \right)\left( {\delta_{\text{pr}} + \varDelta_{\text{pu}} + 2G_{\text{pu}} \sigma_{z}^{(0)} + i} \right)}}{{D^{ * } \left( {\delta_{\text{pr}} } \right)\varGamma_{2}^{2} }}} \right] \\ \chi_{\text{eff}}^{\left( 3 \right)} = & \frac{{\mu \sigma_{10}^{( - 1)} }}{{3\varepsilon_{0} E_{\text{pu}}^{2} E_{\text{pr}}^{ * } }} = \frac{{4f^{3} \mu^{4} \sigma_{z}^{(0)} }}{{3\varepsilon_{0} \hbar^{3} \varGamma_{2}^{3} }} \cdot \frac{{\left( {i - \varDelta_{\text{pu}} } \right)\left( {2i - \delta_{\text{pr}} } \right)\left[ {i + \left( {\varDelta_{\text{pu}} + 2G_{\text{pu}} \sigma_{z}^{(0)} } \right)} \right]}}{{\left[ {i - \left( {\varDelta_{\text{pu}} + 2G_{\text{pu}} \sigma_{z}^{(0)} } \right)} \right]D\left( {\delta_{\text{pr}} } \right)}}, \\ \end{aligned} $$
(6)

where

$$ \begin{aligned} D\left( {\delta_{\text{pr}} } \right) = & \left( {\delta_{\text{pr}} - i\varGamma_{1} /\varGamma_{2} } \right)\left[ {1 + \left( {\varDelta_{\text{pu}} + 2G_{\text{pu}} \sigma_{z}^{(0)} } \right)^{2} } \right]\left[ {\left( {\delta_{\text{pr}} - i} \right)^{2} - \left( {\varDelta_{\text{pu}} + 2G_{\text{pu}} \sigma_{z}^{(0)} } \right)^{2} } \right] \\ & + \frac{{4f^{2} \varOmega_{\text{pu}}^{2} }}{{\varGamma_{2}^{2} }}\left[ {\left( {i - \delta_{\text{pr}} } \right)\left( {1 + \varDelta_{\text{pu}}^{2} } \right) - 2G_{\text{pu}} \sigma_{z}^{(0)} \left( {2iG_{\text{pu}} \sigma_{z}^{(0)} + \varDelta_{\text{pu}} \delta_{\text{pr}} } \right)} \right]. \\ \end{aligned} $$
(7)

and δ pr = δ/Γ 2, Δ pu = Δ/Γ 2, G pu  = µ 2 G/ћΓ2, Ω pu = µE pu/ћ is the generalized Rabi frequency of the pump field. The population inversion of exciton w 0 = 2σ (0)z is determined by a third-order equation

$$ \sigma_{z}^{(0)} + \frac{1}{2} = \frac{{4f^{2} \varOmega_{\text{pu}}^{2} \sigma_{z}^{(0)} }}{{\varGamma_{1} \varGamma_{2} \left[ {1 + \left( {\varDelta_{\text{pu}} + 2G_{\text{pu}} \sigma_{z}^{(0)} } \right)^{2} } \right]}}. $$
(8)

Equation (8) has either a single root or three real roots. The latter case corresponds to optical bistability.

3 Results and discussion

We consider a realistic CdSe QD—Au MNP nanosystem. In this case, ε 0 = 1, ε s  = 6, r = 2.5 nm, R = 7.5 nm, Γ 1 = 1.25 ns−1, Γ 2 = 0.33 ns−1, and µ = 10−28 C m [10, 24]. The exciton resonant frequency is 2.5 eV, which is close to the broad plasmon peak of gold.

To clarify how a coupled QD-MNP nanosystem acts as a bistable device, it is necessary to explain the origin of absorption peak. Figure 2a, b shows linear and nonlinear absorption and refraction spectra of the probe field when the pump field is tuned to exact resonance with the SQD, i.e., Δ pu = 0 (ω 10 = ω pu). In Fig. 2a, we note that Imχ (1)eff is always positive, which is due to energy conservation in the hybrid nanosystem [35]. Additionally, the sharp peak for Imχ (1)eff is away from the position ω pr = ω pu (δpr = 0) as a result of the energy transfer between SQD and MNP via exciton–plasmon interaction. We also find that nonlinear absorption Imχ (3)eff spectrum exhibits three interesting peaks, which are attributed to three-photon resonance, the Rayleigh resonance and ac-Stark effect resonance, respectively [28, 34]. As we expect, the linear absorption peak locates at the position of three-photon resonance, which suggests that Imχ (1)eff is strongly modified by three-photon effect. As demanded by nonlinear Kramers–Kronig relation, the nonlinear refraction spectrum in Fig. 2b displays an obvious complementary behavior in Fig. 2a. Figure 2c gives the origin of these new features. Due to the strong pump field and the exciton–plasmon interaction, the energy levels of the two-level SQD are split into two pairs of dressed states. The members of each pair are separated by a detuned Rabi frequency \( \varOmega^{\prime} = \left\{ {1 + \left( {\varDelta_{\text{pu}} + 2G_{\text{pu}} \sigma_{z}^{(0)} } \right)^{2} + 2\frac{{\varGamma_{1} }}{{\varGamma_{2} }} + \frac{{4f^{2} \varOmega_{\text{pu}}^{2} }}{{\varGamma_{2}^{2} }}\left( {\frac{{\varDelta_{\text{pu}}^{2} + 2G_{\text{pu}} \sigma_{z}^{(0)} \varDelta_{\text{pu}} }}{{1 + \left( {\varDelta_{\text{pu}} + 2G_{\text{pu}} \sigma_{z}^{(0)} } \right)^{2} }}} \right)} \right\}^{1/2} , \)which is determined by the parameter D(δ pr). This Rabi frequency Ω′ is obviously different from the one in the naked atomic system [34]. The origin of three-photon resonance is shown by a transition from the lowest dressed level to the highest dressed level. In this process, the SQD absorbs two pump photons and emits a photon at frequency ω pu − Ω′. Moreover, the SQD will experience a usual excitonic absorption resonance as modified by the ac-Stark effect at frequency ω pu + Ω′. Nonlinear optical response at the position of Rayleigh resonance (ω pr = ω pu) has been studied extensively in the literature [24–26]. In the following, we focus on the dynamical evolution of optical bistability induced by three-photon effect in the nanosystem at ω pr − ω pu < 0.

Fig. 2
figure 2

a Linear and nonlinear absorption Imχ (1)eff , Imχ (3)eff and b Linear and nonlinear refraction Reχ (1)eff , Reχ (3)eff as a function of ħ(ω pr − ω pu) when ω pu = ω 10 (Δ pu = 0). c New features in the spectrum shown in Fig. 2a are identified by the corresponding transition between four dressed states of the SQD. The strong pump field and the plasmon field are used to split both the ground state and the first excited state into a pair of dressed states separated by a Rabi frequency Ω′. TP three-photon resonance, RL Rayleigh resonance, AC ac-Stark resonance

Full size image

In order to plot the dynamical evolution figure of the bistability region, we show the variation of population inversion w 0 versus interparticle distance d. We assume that if d b0 ≤ d ≤ d b1, a bistable effect just appears. Here, d b0 and d b1 are called as the low and high bistability thresholds, respectively. The results presented in Fig. 3a show that for S α  = −1, the bistable effect is always absent despite Δ c increases from −3 to −1. As Δ c = 0, a narrow bistability region locates at [18, 18.26] nm emerges. As Δ c further increases from 0 to 3; however, the region is broadened and shifted to a smaller d b1. For S α  = 2, the bistability region is 2.4 times wider than that for S α  = −1 when Δ c = 3, as shown in Fig. 3b.

Fig. 3
figure 3

Population inversion w 0 as a function of the interparticle distance d with a S α  = −1 and b S α  = 2 for different values of Δ pu. c Low (high) bistability threshold d b0 (d b1) and the width of bistability region d b1 − d b0 as a function of the detuning Δ pu with S α  = −1 and S α  = 2. The other parameters are I pu = 1.13 × 102 W/cm2 and ħ(ω pu − ω pr) = 0.01 meV

Full size image

To obtain optimal parameters for designing optical bistable device, Fig. 3c shows how the bistability thresholds (d b0 and d b1) and the width of bistability region |d b1 − d b0| change with the exciton–pump detuning Δ pu when S α  = −1 and S α  = 2. For S α  = −1, both d b0 and d b1 decrease and d b1 − d b0 increases as Δ pu varies from −0.15 to 10; when Δ pu ≤ −0.15 (d b0 = d b1); however, the bistable region is smeared out. For S α  = 2, d b0 and d b1 exhibit similar behaviors, and the left critical value of Δ pu moves to -0.47. It is obvious that d b1 − d b0 for S α  = 2 is always larger than that for S α  = −1, which suggests that the proposed bistable device is sensitive to the polarization direction of the applied field.

To provide further insight into optical bistability, we study the impact of the pump field intensity I pu on population inversion w 0 for d = 16 nm. Similar to the above definitions, I pu0 and I pu1 correspond to the low and high bistability thresholds of the pump field intensity, respectively. For S α  = −1, we find that the larger the Δ pu is, the easier the bistable effect happens. Moreover, a monotonic curve gradually evolves into a standard S-shaped bistable curve as Δ pu increases from −3 to −1 in Fig. 4a, while for S α  = 2, a series of bistable curves are obtained as Δ pu increases from −3 to 3 (see Fig. 4b).

Fig. 4
figure 4

a Population inversion w 0 as a function of the pump field intensity I pu with (a) S α  = −1 and b S α  = 2 for different values of Δ pu. c Low (high) bistability threshold I pu0 (I pu1) and the width of bistability region I pu1 − I pu0 as a function of the detuning Δ pu with S α  = −1 and S α  = 2. The other parameters are d = 16 nm and ħ(ω pu − ω pr) = 0.01 meV

Full size image

To better visualize the bistable switching process, we consider the dependences of bistability thresholds I pu0 and I pu1 on the detuning Δ pu. To clarify this, in Fig. 4c we find that for S α  = −1, a bistable effect arises as Δ pu varies from −1 to 8.5, and the width of bistability region I pu1 − I pu0 reaches a maximum at Δ pu ≈ 0.8; while for S α  = 2, the adjustable range for optical bistability becomes much wider than that for S α  = −1, and I pu1 − I pu0 gets to the maximum at Δ pu ≈ 0.8. It is interesting that for S α  = −1, the bistable effect is suppressed as −5 ≤ Δ pu < −1. In this region, the nanosystem can serve as a quantum switch. The switch can be turned on and off by switching the polarization direction of the pump field.

Under the same conditions as those of Fig. 4, the induced bistable nonlinear absorption and refraction spectra are depicted in Fig. 5. For S α  = −1, when the pump field is near resonant with the exciton (Δ pu = 0.8), the bistable nonlinear absorption curve traces out an interesting path ①→②→③→④→⑤→⑥ by screening the value of I pu (see Fig. 5a). The bistable refraction response curve in Fig. 5c exhibits a complementary behavior of Fig. 5a, corresponding to the nonlinear Kramers–Kronig relation. In addition, we find that the maximum ratio of nonlinear absorption (refraction) in the upper and lower stable branches under the same conditions can reach 104 (23). However, for S α  = 2, the adjustable region for bistability becomes wider than that for S α  = −1. It is obvious that the bistable absorption and refraction curves are quite different from those in Ref. [28], which are mainly due to the three-photon effect. It is clear that the nonlinear optical responses can be adjusted by the interaction between SQD and MNP and the total field. The effective field applied to the hybrid system is the superposition between the external field and the induced internal field. The interference between the external field and the induced internal field will affect the nonlinear optical responses, while the polarization direction will affect the interference [11]. Hence, the polarization dependences of bistable nonlinear absorption and refraction spectra are two related results of such interference.

Fig. 5
figure 5

Polarization dependences of bistable nonlinear absorption Imχ (3)eff (a, b) and refraction Reχ (3)eff (c, d) with S α  = −1 and S α  = 2. The other parameters are Δ pu = 0.8, d = 16 nm and ħ(ω pu − ω pr) = 0.01 meV

Full size image

4 Conclusion

In conclusion, we have proposed a theoretical model for a tunable bistable device based on a coupled SQD–MNP nanosystem. We have shown that it is easy to turn on or off the optical bistable effect in such system by switching the polarization direction of the pump field, and the bistability thresholds depend strongly on the intensity, frequency, polarization direction of the pump field, and the distance between two nanoparticles. Moreover, we have found that the ratio of nonlinear optical absorption in the two stable states can reach 104, which is so high that our nanosystem can be used as an optical memory cell with two logical states 0 and 1.