Electron acceleration to GeV energy by a chirped laser pulse in vacuum in the presence of azimuthal magnetic field

Abstract

Electron acceleration by a frequency-chirped circularly polarized (CP) laser pulse in vacuum in the presence of azimuthal magnetic field has been studied. A laser pulse propagating along +z-axis interacts with a pre-accelerated electron injected at a small angle in the direction of propagation of laser pulse in vacuum. The electron is accelerated with high energy in the presence of azimuthal magnetic field till the saturation of betatron resonance. A linear frequency chirp increases the duration of interaction of laser pulse with electron and hence enforces the resonance for longer duration. The presence of azimuthal magnetic field further improves the electron acceleration by keeping the electron motion parallel to the direction of propagation for longer distances. Thus, resonant enhancement appears due to the combined effect of chirped CP laser pulse and azimuthal magnetic field. An electron with few MeV of initial energy gains high energy of the order of GeV. Higher energy gain is obtained with intense chirped laser pulse in the presence of azimuthal magnetic field.

1 Introduction

The theoretical and experimental studies of electron acceleration by laser have been fascinating field of research for last few decades [1–5]. These studies explore the techniques for the higher energy gains through laser-driven electron acceleration in vacuum and plasmas. Malka et al. [1] reported experimentally the vacuum acceleration of electrons to MeV energies by a high-intensity subpicosecond laser pulse (10¹⁹ W/cm², 300 fs). Geddes et al. [2] observed a high-quality electron beam from a laser wake field accelerator using a plasma channel guiding. They proposed peak energy in simulation of about 200 MeV which is close to experimental results. An electron in vacuum may be accelerated by the laser field directly. A planar-laser pulse cannot be used for electron acceleration; since it overtakes an electron, the latter is ponderomotively driven forwards in the raising part, but then backwards in trailing part, resulting in no net gain by the electron [6]. An electron can gain and retain significant energy if a magnetic field of suitable magnitude and period is externally applied. The magnetic field strengthens the cyclotron oscillations due to $\vec{v} \times \vec{B}$ force and hence contributes significantly to forward drift and rate of gain of electron energy. The electron energy gain of 1.2 GeV was obtained [7] with an intense laser pulse peak intensity of 8 × 10²¹ W/cm². The characteristics variations in polarizations of laser pulse were studied to investigate the betterment in interaction of laser pulse with electron for high energy gain [8–10]. Sohbatzadeh and Aku [8] proposed that the circularly polarized (CP) laser pulse is more efficient in electron bunch acceleration in comparison with elliptical and linear polarizations. The pulse parameters of interaction with electrons are time-averaged with circular polarization which increases the interaction of laser pulse with electrons. Gupta et al. [10] observed the electron energy gain of 1.5 GeV with a radially polarized laser pulse in the presence of magnetic field of about 1 MG. After attaining the maximum energy gain, the electron gets decelerated, losses energy, and tends to get out of phase with the field even with high-intensity laser pulse. A pre-accelerated electron was employed to enforce a confined trajectory for longer duration [9] with a CP laser pulse. It is easier to inject a pre-accelerated electron in vacuum than in a plasma. Khachatryan et al. [11] evaluated the transverse and longitudinal momentum dynamics for the interaction of free charged particles with a chirped electromagnetic pulse and obtained final longitudinal momentum corresponding to energy 8.55 MeV for electron acceleration with linearly chirped pulse. Liu et al. [12] proposed the additional acceleration and collimation of relativistic electron beams by intense linearly polarized (LP) laser pulse in plasma. They observed a self-generated azimuthal magnetic field of about 100 MG during laser plasma interaction and stated that the additional acceleration is the result of laser magnetic resonance acceleration (LMRA) around the peak of the azimuthal magnetic field. The interaction of relativistic strong laser pulses with electron along with hundreds of MG azimuthal quasistatic magnetic field is a complex process, and a manipulation of 100 MG magnetic field may not be easy in plasma. The resonant enhancement of electron energy was obtained with a frequency-chirped plane-polarized laser pulse in an azimuthal magnetic field in plasma [13] and concluded that the magnetic field for which resonance occurs increases with plasma density. Such increasing magnetic field can be neglected in vacuum. Vacuum acceleration has some advantages over plasma as higher group velocity of a laser and absence of plasma instabilities in vacuum which provides a better platform for electron laser interaction in vacuum than plasma. Hartemann et al. [14] compared the energy in the drive laser pulse to the kinetic energy acquired by 1 nC electron bunch in the inverse free electron laser and found the energy transferred to the beam is 16.6 % of the chirped pulse laser energy. However, they proposed a compact vacuum laser accelerator capable of accelerating picosecond electron bunches with a high gradient (GeV/m) and very low energy spread. Afhami and Eslami [15] have analyzed the effect of nonlinear chirped Gaussian laser pulse on plasma wake field generation. They considered different types of chirped pulse with linear, nonlinear, and periodic characteristics to evaluate the wake field excitation behind the laser pulse. The more oscillation of the main pulse leads to decreasing behavior of wake field generation. The characteristic variation frequency chirp such as linear and quadratic chirp further improves the energy gain [16–19]. Galow et al. [20] proposed a scheme for vacuum autoresonance laser acceleration (ALA) by a CP laser pulse in the presence of axial magnetic field. They observed an acceleration gradient of above 2.2 GeV/m with laser peak intensity of about 10¹⁸ W/cm² (peak power ∼ 10 PW) and axial magnetic field strength of about 60 T.

In this paper, we present the results of a relativistic three-dimensional single-particle code for electron acceleration by a chirped CP laser pulse in the presence of an azimuthal magnetic field in vacuum. In comparison with the model presented by Galow et al. [20], we have employed the azimuthal magnetic field in place of axial magnetic field and observe the electron acceleration at comparatively low values of magnetic field. Additionally, we have examined the effect of linear chirp for electron acceleration by CP laser pulse in vacuum. The efficiency of energy transfer in CP laser pulse is higher than that in case of LP laser pulse. For a suitable position of the peak of the laser pulse, the ponderomotive force due to the laser pushes the electron forward and electron get accelerated rapidly. The linear frequency chirp increases the duration of interaction of laser pulse with electron which maintains the resonance for longer duration. The azimuthal magnetic field having pinching effect which keeps the motion of electron parallel to the direction of propagation for larger distances. Hence, the electron not only gains much higher energy at resonance with optimum values of the magnetic field but also retains the high energy for larger distance even after passing of the laser pulse. Using a pre-accelerated electron of few MeV of initial energy, an energy gain of the order of GeV is observed in the presence of relatively smaller azimuthal magnetic field of the order of 100 kG with a linearly chirped CP laser pulse of relatively smaller intensities in vacuum.

We examine the electron dynamics in the presence of an azimuthal magnetic field with frequency-chirped CP laser in vacuum in Sect 2. We solve the coupled differential equations numerically by using a simulation code to find the electron trajectory and energy in vacuum and discussed the numerical results in Sect. 3. A conclusion of results is given in Sect. 4.

2 Electron dynamics and relativistic analysis

We consider a chirped CP laser pulse propagating in the z-direction with transverse components of electric field ($\vec{E} = \hat{x}E_{x} + \hat{y}E_{y}$) given as:

$$E_{x} = \frac{{E_{0} }}{f}\sin (\varphi )\exp \left( { - \frac{{\left( {\xi - \xi_{0} } \right)^{2} }}{{\sigma^{2} }} - \frac{{r^{2} }}{{r_{0}^{2} f^{2} }}} \right)$$

(1)

$$E_{y} = \frac{{E_{0} }}{f}\cos (\varphi )\exp \left( { - \frac{{\left( {\xi - \xi_{0} } \right)^{2} }}{{\sigma^{2} }} - \frac{{r^{2} }}{{r_{0}^{2} f^{2} }}} \right)$$

(2)

where φ = k(ξ)ξ + tan⁻¹(z/Z _R ) − zr ²/(Z _R r ²₀ f ²) + φ ₀, f ² = 1 + (z/Z _R )², k(ξ) = ω(ξ)/c is the wave number, ω(ξ) is an arbitrary frequency chirp and is equal to ω ₀(1 + αξ) for linear [15] and negative chirp, α is the frequency chirp parameter, Z _R  = kr ²₀ /2 is the Rayleigh length, ξ = z − ct is the retarded coordinate, φ ₀ is the initial phase, σ is the pulse length, r ² = x ² + y ², r ₀ is minimum laser spot size, ω ₀ is the laser frequency, ξ ₀ is the initial position of the pulse peak, and c is the velocity of light in vacuum minimum. The laser spot size r ₀ is assumed to be same for all frequency components. The spatial variations of field in transverse direction give rise to a longitudinal field component. The longitudinal component of electric field is obtained as E _z  = −(i/k)( ∂ E _x / ∂ x + ∂ E _y / ∂ y). The longitudinal component is smaller by a factor of (1/k) compared to dominant transverse field components. Thus, we have neglected the longitudinal component of electric field because of very small amplitude in comparison with transverse component [7]. The magnetic field components of the laser pulse can easily be deduced through Maxwell’s equations and expressed as:

$$\vec{B} = - ic\frac{{\vec{\nabla } \times \vec{E}}}{\omega (\xi )}$$

(3)

The laser pulse imparts energy to the electron that carries current in the z-direction and experiences an azimuthal magnetic field. Liu et al. [12] observed a self-generated azimuthal magnetic field of about 100 MG during laser plasma interaction. Such self-generated field is feasible to apply from external source in vacuum. Takakura et al. [21] have proposed a model for generation of azimuthal magnetic field. This externally applied azimuthal magnetic field [13, 22] is expressed as:

$$\vec{B}_{\theta } = \left( {y\hat{x} - x\hat{y}} \right)\frac{{B_{0} }}{{r_{0} }}\exp \left( { - \frac{{r^{2} }}{{r_{0}^{2} }}} \right)$$

(4)

where the constant B ₀ represents the maximum amplitude of magnetic field. The azimuthal magnetic field rises from zero at r = 0 to a maximum around r ~ r ₀. Figure 1 shows a schematic of electron acceleration by a chirped CP laser pulse in the presence of an azimuthal magnetic field in vacuum.

Fig. 1

A schematic showing the vacuum acceleration of electron by a chirped CP laser pulse in the presence of azimuthal magnetic field

The equations governing electron momentum and energy are as follows:

$$\frac{{{\text{d}}p_{x} }}{{{\text{d}}t}} = - eE_{x} + e\beta_{z} B_{y} + e\beta_{z} B_{\theta y}$$

(5)

$$\frac{{{\text{d}}p_{y} }}{{{\text{d}}t}} = - eE_{y} - e\beta_{z} B_{x} - e\beta_{z} B_{\theta x}$$

(6)

$$\frac{{{\text{d}}p_{z} }}{{{\text{d}}t}} = - e\left( {\beta_{x} B_{y} - \beta_{y} B_{x} } \right) - e\left( {\beta_{x} B_{\theta y} - \beta_{y} B_{\theta x} } \right)$$

(7)

$$\frac{{{\text{d}}\gamma }}{{{\text{d}}t}} = - e\left( {\beta_{x} E_{x} + \beta_{y} E_{y} } \right)$$

(8)

where p _x , p _y , and p _z are x, y, and z components of the momentum $\vec{p} = \gamma m_{0} \vec{v}$, respectively; β _x , β _y , and β _z are x, y, and z components of the normalized velocity $\vec{\beta } = \vec{v}/c$, respectively; γ ² = 1 + (p ² _x  + p ² _y  + p ² _z )/(m ₀ c)² is the Lorentz factor; and −e and m ₀ are the electron’s charge and rest mass, respectively. The following are the dimensionless variables: $a_{0} \to \frac{{eE_{0} }}{{m_{0} \omega_{0} c}}$, τ → ω ₀ t, $\sigma^{{\prime }} \to \frac{{\omega_{0} \sigma }}{c}$, $r_{0}^{{\prime }} \to \frac{{\omega_{0} r_{0} }}{c}$, $z_{0}^{{\prime }} \to \frac{{\omega_{0} z_{0} }}{c}$, $x^{{\prime }} \to \frac{{\omega_{0} x}}{c}$, $y^{{\prime }} \to \frac{{\omega_{0} y}}{c}$, $z^{{\prime }} \to \frac{{\omega_{0} z}}{c}$, $\beta_{x} \to \frac{{v_{x} }}{c}$, $\beta_{y} \to \frac{{v_{y} }}{c}$,$\beta_{z} \to \frac{{v_{z} }}{c}$, $p_{0}^{\prime } \to \frac{{p_{0} }}{{m_{0} c}}$, $p_{x}^{\prime } \to \frac{{p_{x} }}{{m_{0} c}}$, $p_{y}^{\prime } \to \frac{{p_{y} }}{{m_{0} c}}$, $p_{z}^{\prime } \to \frac{{p_{z} }}{{m_{0} c}}$, $k_{0}^{{\prime }} \to \frac{{ck_{0} }}{{\omega_{0} }}$, $\alpha^{{\prime }} \to \frac{\alpha c}{{\omega_{0} }}$, and $b_{0} \to \frac{{eB_{0} }}{{m_{0} \omega_{0} c}}$.

Equations (5)–(8) are the coupled ordinary differential equations. We solve these equations numerically for electron trajectory and energy. We assume that the electron is initially injected [9] at a small angle δ to the direction of propagation of laser pulse with $\vec{p}_{0} = \hat{x}p_{0} \sin \delta + \hat{z}p_{0} \cos \delta$ where p ₀ is the initial momentum of the electron.

3 Results and discussion

We have chosen the following dimensionless parameters for numerical analysis: a ₀ = 2.5 (corresponding to laser intensity I ∼ 1.7 × 10¹⁹ W/cm²), a ₀ = 5 (corresponding to laser intensity I ∼ 6.92 × 10¹⁹ W/cm²) and a ₀ = 10 (corresponding to laser intensity I ∼ 2.74 × 10²⁰ W/cm²) with wave length λ ₀ ∼ 1 μm; $r_{0}^{{\prime }} = 900$ (corresponding to laser spot sizes r ₀ ∼ 151 μm); and $p_{0}^{{\prime }} = 1$, 1.5, 2, and 2.5; $\sigma^{{\prime }} = 70$ (corresponding to laser pulse duration of 200 fs); $\delta = 10^{{^\circ }}$; φ ₀ = 0; b ₀ = 0.0005 (corresponding to a magnetic field of 53 kG), b ₀ = 0.001 (corresponding to a magnetic field of 106 kG), and b ₀ = 0.005 (corresponding to a magnetic field of 534 kG); and $z_{0}^{{\prime }} = - 300$.

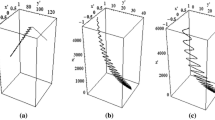
Figure 2 shows the electron trajectory in three-dimensional planes in the absence and presence of chirping. The electron rotates around the direction of propagation of laser pulse during interaction with laser pulse in the presence of magnetic field. The magnetic field enhances the strength of $\vec{v} \times \vec{B}$ force.

Fig. 2

Electron trajectory in 3D plane in the absence and presence of chirping for CP laser pulse for a ₀ = 2.5, b ₀ = 0.005 and $p _{0}^{{\prime }} = 1$. (a) $\alpha^{{\prime }} = 0$ and (b) $\alpha^{\prime } = 0.003$. The other parameters are $r_{0}^{{\prime }} = 900$, $\sigma^{{\prime }} = 70$, ϕ ₀ = 0, δ = 10^∘ and $z_{0}^{{\prime }} = - 300$

Gupta and Ryu [9] proposed that the electron traverse more distance in the direction of propagation of laser pulse in the presence of obliquely incident magnetic field with normalized values b ₀ = 0.1 and 0.01. In the absence of chirping, the electron, after attaining the maximum energy gain, retains the gain till saturation of betatron resonances. Afterward, it is decelerated slowly with decrease in radius as shown in Fig. 2a. The frequency-chirped laser pulse supports better interaction between the laser pulse and the electron. It enforces a very small divergence in electron trajectory as shown in Fig. 2b. Hence, it maintains the resonance for longer durations. The combined effect of chirping and pinching supports the resonant enhancement of higher energy gains for relatively larger distances in the presence of relatively smaller magnetic field of normalized value b ₀ = 0.005 (corresponding to a magnetic field of 534 kG).

Figure 3 shows the variation of energy gain γ as a function of normalized magnetic field b ₀. In Fig. 3a, b, electron energy gain has been analyzed at different values of normalized initial momentum with and without chirping for a ₀ = 2.5 and 5, respectively. Higher energy gain appears with chirped laser pulse than that with unchirped laser pulse in the presence of azimuthal magnetic field. As shown in Fig. 3a for a ₀ = 2.5 and $p_{0}^{{\prime }} = 1.5$, the energy gain is γ = 1042 in the presence of chirp factor $\alpha^{{\prime }} = 0.0015$ which is about 65 % higher than that of γ = 630 in the absence of chirping. In Fig. 3b, for a ₀ = 5 and $p_{0}^{{\prime }} = 1.5$, the electron energy gain is γ = 3111 in the presence of chirp factor $\alpha^{{\prime }} = 0.0011$ which is 18 % higher than that of γ = 2632 in the absence of chirping. This is the minimum predicted energy gain with a set of parameters. For such energy gain, the value of optimum magnetic field is taken as b ₀ = 0.00165 (corresponding to 176 kG) in the presence of chirping which is 60 % smaller than b ₀ = 0.005(corresponding to 534 kG) to achieve a high energy gain in the absence of chirping. The normalized initial momentum is optimized for high energy gain. The high energy gain for a ₀ = 2.5 appears with $p_{0}^{{\prime }} = 2.5$, whereas for a ₀ = 5, it appears with $p_{0}^{{\prime }} = 1.5$. This is because the acceleration gradient decreases with initial momentum and increases with laser pulse intensity. Thus, with higher values of intensity, the optimum value of initial momentum for high energy gain appears to be small and vice versa.

Fig. 3

Energy gain γ as a function of normalized magnetic field b ₀ for different values of normalized initial momentum and intensity parameters for CP laser pulses. a $p_{0}^{{\prime }} = 1.5$, 2, and 2.5 at a ₀ = 2.5 with $\alpha^{{\prime }} = 0$ and $\alpha^{{\prime }} = 0.0015$, b $p_{0}^{{\prime }} = 1.5$, 2, and 2.5 at a ₀ = 5 with $\alpha^{{\prime }} = 0$ and $\alpha^{{\prime }} = 0.0011$, and c a ₀ = 6, 7.5, 10, 12.5, 15, and 20 at $p_{0}^{{\prime }} = 1.5$ with $\alpha^{{\prime }} = 0.000975$, 0.00088, 0.00078, 0.000725, 0.00069, and 0.00065, respectively. The other parameters are same as taken in Fig. 2

Figure 3c shows the variation of energy gain γ with b ₀ for different values of laser pulse intensity parameters a ₀ = 6, 7.5, 10, 12.5, 15, and 20 at p ₀ = 1.5 and suitable values of chirp factor. In order to obtain high energy gain, the optimum value of magnetic field remains small with higher values of laser pulse intensity. A pre-accelerated electron is trapped with laser pulse in the presence of low and optimum magnetic field. After attaining maximum gain at resonance, the electron energy decreases and almost saturates for the larger values of magnetic field. The optimum value of magnetic field corresponding to laser pulse intensity for the maximum energy gain appears with optimized chirp parameter. The energy gain increases with laser pulse intensity. For a ₀ = 20, the energy gain γ = 5210 appears at b ₀ = 0.000875 which is higher than γ = 5052 for a ₀ = 15 at b ₀ = 0.0009 with $p_{0}^{{\prime }} = 1.5$. The appeared values of normalized magnetic field for high energy gain are feasible and can be produced experimentally [23, 24].

Figure 4 shows the variation of electron energy gain γ as a function of the normalized distance $z^{{\prime }}$. In Fig. 4a, b, we see the variation of γ with $z^{{\prime }}$ in the absence and presence of chirping for different values of normalized momentum $p_{0}^{{\prime }} = 1.5$, 2, and 2.5 with optimum values of magnetic field for a ₀ = 2.5 and a ₀ = 5, respectively. A pre-accelerated electron has sufficient kinetic energy to gain high energy during acceleration. The magnetic field enhances the strength of $\vec{v} \times \vec{B}$ force exerted on the electron and maximizes the electron energy gain. After attaining the maximum energy gain, it is saturated for larger distances. It is because of the betatron oscillations set up between the electron and the electric field of the laser pulse which enforces the electron to retain maximum energy even after passing of laser pulse. One can clearly see from Fig. 4a, b that the electron retains high energy for larger distance in the presence of frequency chirp. In the absence of chirping, the electron gains and retains relatively lower energy for relatively smaller distance than that in the presence of chirped laser pulse. Figure 4c shows the variation of energy gain γ with $z^{{\prime }}$ for the different values of intensity parameter a ₀ = 6, 7.5, 10, 12.5, 15, and 20 at $p_{0}^{{\prime }} = 1.5$ with optimum values of magnetic field b ₀ derived from Fig. 3c, and suitable chirp parameter is same as taken in Fig. 3c.

Fig. 4

Energy gain γ as a function of normalized distance $z^{{\prime }}$ for different values of normalized initial momentum $p_{0}^{{\prime }}$ and intensity parameters a ₀ for CP laser pulses. a $p_{0}^{{\prime }} = 1.5$, 2, and 2.5 at a ₀ = 2.5 with $\alpha^{{\prime }} = 0$ and $\alpha^{{\prime }} = 0.0015$, b $p_{0}^{{\prime }} = 1.5$, 2 and 2.5 at a ₀ = 5 with $\alpha^{{\prime }} = 0$ and $\alpha^{{\prime }} = 0.0011$, and c a ₀ = 6, 7.5, 10, 12.5, 15, and 20 at $p_{0}^{{\prime }} = 1.5$ with b ₀ = 0.00145, 0.0012, 0.001, 0.00095, 0.0009, and 0.000875 and $\alpha^{{\prime }} = 0.000975$, 0.00088, 0.00078, 0.000725, 0.00069, and 0.00065, respectively. The other parameters are same as taken in Fig. 2

With the optimum value of magnetic field, initial momentum and suitable chirp parameter, the electron gains higher energy. It is clear that the higher energy gain is observed with higher values of laser pulse intensity. An acceleration gradient of the order of GeV/m was observed by Galow et al. [20] by using CP laser pulse in the presence of axial magnetic field of about 60 T. We employ an azimuthal magnetic field of about 9.4 T with chirped CP laser pulse in vacuum to attain the same order of acceleration gradient.

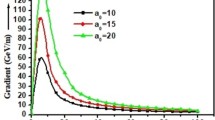
Figure 5 shows the variation of acceleration gradient as a function of distance z. The acceleration gradient [20] can be obtained by using relation ${\text{d}}\gamma /{\text{d}}z = - e\vec{\beta } \cdot \vec{E}/\beta_{z}$ and is plotted with distance z for a chirped CP laser pulse for different values of intensity parameter a ₀ = 2.5, 5, 10, and 20 with normalized initial momentum $p_{0}^{{\prime }} = 1.5$ and optimum values of magnetic field b ₀ as derived from Fig. 3, and suitable chirp parameter α is same as taken in Fig. 3. Sohbatzadeh et al. [17] reported an acceleration gradient of 59 GeV/m using a chirped femtosecond laser pulse with intensity 10¹⁹ W/cm². However, we have observed an acceleration gradient of about 62 GeV/m with a ₀ = 2.5(corresponding to laser intensity I ∼ 1.7 × 10¹⁹ W/cm²). Higher acceleration gradient is seen with higher values of laser intensity parameter. Further the emittance and radiative loss remain small with higher intensity pulses, as the radiative loss is not much with the pre-accelerated electron [9]. The final momentum of emitted electron with maximum energy gain is related to emittance angle θ. Using relation tan θ = (p ² _x  + p ² _y )^1/2/p _z with Lorentz factor, the angle of emittance with respect to z-axis can be written as $\theta = \tan^{ - 1} \sqrt {((\gamma^{2} - 1)/\gamma^{2} \beta_{z}^{2} ) - 1}$. For energy gain of 1.5 GeV with a ₀ = 5, the angle of emittance is 0.84^∘, and for energy gain of 2.66 GeV with a ₀ = 20, the angle of emittance is 0.64^∘. The obtained values of angle of emittance remain small for higher energy gain.

Fig. 5

Acceleration gradient and energy gain γ as a function of distance z for CP laser pulse with intensity parameter a ₀ = 2.5, 5, 10, and 20 for$p_{0}^{{\prime }} = 1.5$ and optimum values of magnetic field and chirp parameters. The other parameters are same as taken in Fig. 2

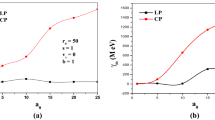
Figure 6 shows the electron energy gain γ calibration curve. The figure exhibits the variation of normalized magnetic field b ₀, chirp parameter $\alpha^{{\prime }}$ and energy gain γ as a function of intensity parameter a ₀ with $p_{0}^{{\prime }} = 1.5$. The optimum values of magnetic field and chirping factor decrease for attaining higher energy gain at high intensity. However, in order to attain maximum energy gain of 2.4 GeV at a ₀ = 10(corresponding to laser intensity I ∼ 2.74 × 10²⁰ W/cm²), the optimum values of magnetic field and chirp parameter are found 0.001 (corresponding to a magnetic field of 106 kG) and 0.00078 respectively.

Fig. 6

Energy gain γ calibration curve. For normalized magnetic field b ₀, chirping parameter $\alpha^{{\prime }}$ and normalized energy gain γ as a function of normalized intensity a ₀. The other parameters are same as taken in Fig. 2

The presented single particle simulations are supported by many particle simulations also. However, the exit energy gain for an ensemble of electrons is slightly different from that for single electron acceleration [8]. It is because of the Coulomb electron–electron interactions. The mean exit energy gain remains same with and without considering electron–electron interactions [20]. For an ensemble of electrons, the polarization state and initial characteristics of electrons play important role in electron acceleration with a chirped laser pulse in vacuum. CP laser pulse can efficiently accelerate the electrons of a poor quality electron bunch [8] with very low energy spread. Thus, the presented model of electron acceleration by chirped CP laser pulse in the presence of azimuthal magnetic field holds equally effective for an ensemble of particles.

4 Conclusion

The present study highlights the importance of chirped CP laser pulse and azimuthal magnetic field to obtain high electron energy gain in vacuum. We have observed an energy gain of γ = 5210(corresponding to 2.66 GeV) for laser intensity a ₀ = 20(corresponding to 2.74 × 10²⁰ W/cm²) with chirp parameter $\alpha^{{\prime }} = 0.00065$ in the presence of azimuthal magnetic field b ₀ = 0.000875 (corresponding to 94 kG). Thus, a pre-accelerated electron of few MeV of initial energy can be accelerated up to GeV energy with optimized laser and magnetic field parameters as we have analyzed in the present study.