1 Introduction

Dynamic population control inside erbium-doped fiber amplifiers (EDFAs) has been actively studied [1]. Dynamic population grating filters have been experimentally demonstrated using two counter-propagating fields in a fiber amplifier [2, 3]. This technique makes it possible to obtain a filter with variable parameters. The readout of optical bit-patterns stored via two-pulse interference was realized using a third nanosecond pulse in an EDFA [4]. A flip-flop memory based on transparency and absorption-based binary states in a fiber amplifier has been proposed in [5]. The effects of phase modulation on local gain saturation in doped fibers have been studied using Sagnac interferometers [6, 7]. In these phenomena, the erbium population difference between the ground level 4I15/2 and the metastable level 4I13/2 was controlled dynamically by introducing resonant pulses. When this type of amplifier is initially pumped, i.e., when the erbium population is in the population inversion condition, the population can be changed from the gain condition to the gain saturation condition through stimulated emission. To enable application of such dynamic effects, it is essential to evaluate the temporal behavior of amplifier gain. In particular, the transition time between the two conditions should be one of the main parameters to be studied.

We have previously proposed time-resolved measurement techniques to probe the transient populations of EDFAs using a directly modulated laser diode as a light source. Direct modulation of the laser diode allowed us to obtain the variable pulse parameters freely, including the pulse width, the pulse number, and the pulse interval. The population recovery time in an EDFA was measured via a pump–probe technique [8]. A self-probe method was also applied to study gain saturation dynamics induced by signal pulses in EDFAs [9, 10].

However, one advantage of the use of EDFAs is their broadband operation with bandwidths of over 30 nm. The transient properties of an EDFA may depend on the wavelength at which the stimulated emission occurs, because the emission and absorption cross sections generally show wavelength dependence. Therefore, a study of the wavelength-dependent gain dynamics will provide significant information that will be useful for a wide range of applications.

In this paper, we report on the wavelength dependence of the transition time from the gain condition to the gain saturation condition as induced by a single signal pulse in an EDFA. To evaluate the transition time, we applied a self-probe method using a tunable laser diode array that was developed for optical communication applications. The dependence is analyzed using a combination of a model that describes the temporal evolution of the erbium population at the input end of the fiber and McCumber theory.

2 Self-probe method

We applied the self-probe method reported in [9] to probe the transient gain in EDFAs. This method allows us to obtain a temporal profile of the gain through a simple calculation. In this work, the signal wavelength was fixed at 1.53 μm, where the emission cross section is approximately the same as the absorption cross section [11]. As a result, the model was very simple. However, the two cross sections do not generally coincide with each other. Therefore, we needed to rewrite the model to evaluate the wavelength dependence.

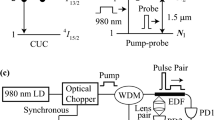
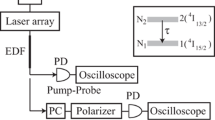
By comparing the input pulse intensity I in and the output pulse intensity I out, we can obtain the time-dependent populations N 1(t) and N 2(t) (see Fig. 1a) as follows

$$\ln \frac{{I_{\text{out}} (t)}}{{I_{\text{in}} (t)}} = \alpha \cdot L \cdot \left[ {\sigma_{\text{s}}^{\text{e}} (\lambda_{\text{s}} )N_{2} (t) - \sigma_{\text{s}}^{\text{a}} (\lambda_{\text{s}} )N_{1} (t)} \right]$$
(1)

where σ es (λ s) and σ as (λ s) are the erbium emission and absorption cross sections at the signal wavelength, respectively. L is the fiber length, and α is a proportional constant that is determined based on the erbium concentration, the interaction area, and the overlap factor in the fiber.

Fig. 1
figure 1

a Energy diagram of erbium ions. N 1 and N 2: populations of levels 1(4I15/2) and 2(4I13/2), respectively. b Experimental setup. FG: function generator, Coupler: 99/1 % coupler, EDFA: erbium-doped fiber amplifier, VA: variable attenuator, PD: photodetector

Full size image

In general, it is difficult to calculate populations analytically in EDFAs, because they change simultaneously with time and position along the fiber length. In [13], the temporal evolution of the populations N 1(t) and N 2(t) in an EDFA was analyzed. However, the model was simplified by neglecting the variations in the amplified pulse and the populations along the propagation direction. As a result, only the time evolution at the input end of the fiber could be obtained. We then apply our model to a discussion of the right-hand side of (1). N 1(t) and N 2(t) are expressed as an exponential function with a time constant of τ 21/(1 + P p/P th + P s/P sat), where P p, P s, and τ 21 are the pump power, the signal power, and the radiative lifetime, respectively, from level 2 to level 1. P th and P sat are the pump threshold and the signal saturation power, respectively. This equation indicates that the time constant becomes shorter with higher input signal and pump powers. By substituting the exponential function into (1), we obtain the following equation:

$$\ln \frac{{I_{\text{out}} (t)}}{{I_{\text{in}} (t)}} \propto \;\exp \left( { - \frac{{1 + P_{\text{p}} /P_{\text{th}} + P_{\text{s}} /P_{\text{sat}} }}{{\tau_{21} }}t} \right).$$
(2)

The pump threshold and the signal saturation power are expressed as

$$P_{\text{th}} = \frac{{h\nu_{\text{p}} A_{\text{p}} }}{{\sigma_{\text{p}}^{\text{a}} \tau_{21} }},\quad P_{\text{sat}} = \frac{{h\nu_{\text{s}} A_{\text{s}} }}{{(\sigma_{\text{s}}^{\text{e}} + \sigma_{\text{s}}^{\text{a}} )\tau_{21} }} ,$$
(3)

where h, ν p,s, and A p,s are the Planck constant, the frequencies of the pump and signal light beams, and the effective area corresponding to the modal overlaps with the fiber core of the pump and signal light beams, respectively. σ ap is the absorption cross section at the pump wavelength. In [13], it was assumed that the absorption cross section σ as and the emission cross section σ es at the signal wavelength were approximately equal; therefore, the saturation power was defined as P sat = hν s A s/2σ s τ 21. In contrast, we need to use P sat as it is shown in (3) to explicitly express the two cross section parameters.

To evaluate the characteristic transition time from the initial gain condition (before signal input at t = 0) to the gain saturation condition (after a steady state with the signal pulse is achieved), we define the decay time constant in the exponential function as the transition time from the gain condition to the gain saturation condition.

3 Experimental

Figure 1a shows our experimental setup. A tunable distributed feedback (DFB) laser array (NTT Electronics: NLK1C7MBLG) was used as a light source. This laser array contains 12-channel laser diodes and a single semiconductor optical amplifier. Each diode has a different oscillation wavelength. In addition, these wavelengths can be tuned by varying the temperature. The laser array covers the wavelength range from 1527 to 1566 nm. In the experiments, the laser temperature was fixed. Therefore, as shown below, the oscillation wavelengths showed a comb-like spectrum. Rectangular-shaped pulses from the laser modulated by a function generator were used as the signal pulses. These pulses were divided into two portions using a 99/1 % coupler. The 1 % pulse was used to monitor the input pulse intensity. The other pulse was introduced into a 980-nm-pumped EDFA (Fiber Labs: AMP-FL8013-CBDB-13) as a signal pulse. The EDFA was 6.5 m long. For all wavelengths, the pulse width, the pulse interval, and the peak intensity of the signal pulse were 1 μs, 1 ms, and 7 mW, respectively. Because the pulse interval was longer than the population recovery time [14], each measurement was performed under single-shot conditions. The pump power of the 980-nm laser was fixed at 50 mW. The amplified pulse profiles were detected using a photodiode after attenuation and were stored using an oscilloscope.

4 Results

First, we show a typical amplified spontaneous emission (ASE) spectrum of an EDFA observed in the propagation direction in Fig. 2a. The emission shows a broad band width from 1530 to 1560 nm due to Stark splitting in the ground level 1 and in the metastable level 2 [15]. Three main peaks are found at 1530, 1543, and 1558 nm. These peaks were identified as transitions from the lowest level of 4I13/2. However, definitive identification of these peaks is difficult, because the transitions from the higher sublevels of 4I13/2 also contribute to the room-temperature emissions [15]. Figure 2b shows the spectrum of the laser. Each peak was obtained by choosing 11 different channels. The oscillation wavelengths were distributed from 1528 to 1559 nm with a step size of 3 nm, thus covering the EDFA emission band.

Fig. 2
figure 2

a ASE spectrum of the EDFA when observed in the propagation direction. b Emission spectrum of the LD array

Full size image

In the self-probe experiments, we took the measurements at the 11 wavelengths indicated in Fig. 2. The left-hand side of Fig. 3a shows a temporal profile of the output pulse at 1528 nm. The instantaneous gain at the pulse front is approximately 25 dB. However, the amplified pulse shapes are deformed from their initial rectangular shape. This indicates that the EDFA gain is sufficiently saturated during pulse amplification. We show ln(I out/I in) as a gray line on the right-hand side of Fig. 3a. The black line in the figure is a result obtained by fitting to an exponential function. The agreement between the experimental and fitted results is reasonably good, and the time constant was determined to be 420 ns. Figure 3b, c show the corresponding profiles at 1543 and 1559 nm, respectively. The black lines are fitting results that were obtained using the same procedure. We can see that the fitted lines reproduce the experimental data well. The time constants at 1543 and 1559 nm were found to be 1.05 and 1.65 μs, respectively. In Fig. 4, the time constants obtained are plotted as a function of the wavelength using open circles. The time constant gradually increases as the wavelength increases.

Fig. 3
figure 3

Output pulse profiles (left) and ln(I out/I in) (right) for wavelengths of a 1528, b 1543, and c 1559 nm. Gray lines denote experimental data, and black lines denote fitting results

Full size image
Fig. 4
figure 4

Wavelength dependence of time constant. Open circles denote experimental data. Dashed line denotes reproduction using (6) combined with cross section given in [11]. Solid line denotes reproduction using (6) combined with the emission spectrum shown in Fig. 2

Full size image

5 Discussion

We now discuss the wavelength dependence of the transition time. From (2) and (3), the time constant is written as:

$$\tau = \frac{{\tau_{21} }}{{1 + P_{\text{p}} /P_{\text{th}} + P_{\text{s}} (\sigma_{\text{s}}^{\text{a}} (\nu_{\text{s}} ) + \sigma_{\text{s}}^{\text{e}} (\nu_{\text{s}} ))\tau_{21} /(h\nu_{\text{s}} A_{\text{s}} )}}.$$
(4)

According to McCumber theory [11, 12], the absorption cross section can be written as

$$\sigma_{\text{s}}^{\text{a}} (\nu ) = \sigma_{\text{s}}^{\text{e}} (\nu )\;\exp ( - (\varepsilon - h\nu ) /kT),$$
(5)

where k and T are the Boltzmann constant and the temperature, respectively. hν is the photon energy. ε is the energy difference between the lowest level of 4I13/2 and the lowest level of 4I15/2. The energy difference is located near the peak emission wavelength, which corresponds to the highest peak at 1529 nm, as shown in Fig. 2 [11]. In this model, the thermal transition in each manifold is assumed to be much faster than transitions between the manifolds. This condition is generally satisfied at room temperature. This relationship thus indicates that the difference between σ es (ν) and σ as (ν) increases for longer wavelengths. By substituting this formula into (4), we can obtain the wavelength (frequency)-dependent transition time of the gain saturation as follows:

$$\tau = \frac{A}{{B + \sigma_{\text{s}}^{\text{e}} (\nu_{\text{s}} )(1 + \;\exp ( - (\varepsilon - h\nu_{\text{s}} ) /kT)) /\nu_{\text{s}} }} ,$$
(6)

where A = hA s/P s and B = hA s(1 + P p/P th)/P sτ21. The dashed line in Fig. 4 is the best fit that could be obtained by varying the parameters A and B. For the fitting procedure, we used values of 6540 cm−1 for ε and 200 cm−1 for kT. For the wavelength-dependent emission cross section σ es (ν), the values from [11] that are shown in Fig. 2 were applied. While the agreement between the experimental results and the fitted line is relatively good, a clear discrepancy can be seen. The solid line in the figure indicates the fitting result obtained by substitution of the wavelength-dependent emission intensity shown in Fig. 2 into σ es (ν). This solid line reproduces the experimental data more closely than the dashed line. In our measurements, the output pulses were amplified along the fiber. As a result, the emission profile that was observed in the propagation direction may be more suitable for use in explanation of the experimental data. We would also like to comment on the validity of applying the McCumber relation to the analysis. The absorption cross section σ as (ν) and the emission cross section σ es (ν) can both be obtained experimentally. Therefore, it is possible to analyze the wavelength dependence of the saturation time constant using these two cross sections. However, the emission spectrum can easily be measured by observing ASE under 980-nm pumping. No additional light source or apparatus are required. Therefore, the McCumber relation allows us to explain the wavelength dependence using simple emission data from a sample that has been tested.

As noted in [13], because the model that was used here was derived while neglecting the propagation length dependence, it is impossible to evaluate the time constant quantitatively. Therefore, we could not compare the agreements between the parameters A and B obtained by fitting and those calculated using the parameters such as A s and P s. However, the model is considerably simplified, and the analytical results nevertheless reproduced the experimental results reasonably well. To obtain a deeper understanding of the gain recovery process, we must examine the variation along the propagation direction. For this purpose, the fiber length dependence of the time constant should be precisely measured, and this will be our next task in this research.

The time constant at the longer wavelength was approximately three times longer than that at the shorter wavelength. In our previous paper, the gain saturation time constant was inversely proportional to the signal power [9]. Therefore, for high-speed population control, higher signal power is required at the longer wavelength.

6 Conclusion

In conclusion, we reported measurements of the transition time of the gain saturation in an erbium-doped fiber amplifier in the wavelength range from 1528 to 1559 nm using a self-probe method. It was found that the transition time was reduced at shorter wavelengths. The wavelength dependence was analyzed using a model that described the temporal evolution of the erbium population at the input end of the fiber combined with McCumber theory.