1 Introduction

Laser-induced incandescence (LII) using both Q-switched pulsed lasers, see, for example [1], and references contained therein, and intra-cavity CW lasers [2] are now established techniques for measuring soot volume fraction (SVF) and, with pulsed lasers, soot primary particle diameter [3].

Very recently the LII techniques were extended to include modulated LII where a chopped laser light source was employed to generate a modulated LII signal in a laminar diffusion flame [4–6]. Unlike the earlier techniques, the modulation of the soot temperature was small and essentially did not perturb the average soot temperature. The soot temperature was then derived from the ratio of the modulated LII signals at two wavelengths and compared favourably to CARS temperature measurements. The authors termed this modulated LII two-colour pyrometry or MOLIIP. The gas flow velocity was also measured, presumably from the phase delay of the modulated LII (MLII) signal with respect to the laser excitation source [7].

We have also performed two-colour MLII measurements by sinusoidal modulating the output of a diode laser in the frequency range 25 Hz–200 kHz in a laminar diffusion flame. The soot temperatures on the centre line of the laminar diffusion flame are shown to be independent of frequency and in agreement with CARS temperature measurements. A theory is developed to describe the phase delay of the MLII signal with respect to the excitation source involving the following parameters: gas replacement time in the MLII sample volume, soot cooling time constant and the SVF. These three parameters and their 95 % confidence limits were derived by a least mean squares fit of the experimental phase delay versus frequency to the theoretical prediction. Time constants for flow replacement, soot cooling and the SVF are derived from the fit to the data and shown to be largely in agreement with the expected values. The extension of this technique to other flames is discussed.

2 Experimental

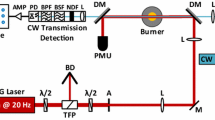
For the MLII measurements, an existing LII system was employed where the general optical receiver layout and details of the equivalent filter approximation employed here have already been described [8], and the experimental layout is shown in Fig. 1. Differences in the receiver and light collection are outlined below.

Fig. 1
figure 1

Top view schematic of the optical layout and detection apparatus

Full size image

Instead of a fibre-optic input, the receiver had a 1-mm aperture. The signal collection optics used a pair of Ross Optical achromats (L-AOC279, 50 mm diameter, 210 mm focal length and L-AOC264, 50 mm diameter, 100 mm focal length, both MgFl2 anti-reflection coated) installed in 50.8 mm diameter Thor Labs lens tubes. A 40-mm-diameter black plastic aperture was mounted between the lenses to limit reflections from tube walls propagating to the detectors. The receiver aperture was approximately 95 mm from the 100-mm focal length lens providing approximately 2:1 imaging of the aperture at the LII measurement location approximately 195 mm from the outer surface of 210-mm focal length lens. The LII light collection axis was 35° in a backward direction from the laser excitation axis. The 35° light collection procedure came from the use of a previous conventional LII system for this work. The departure from 90° increases the signal, but reduces the spatial resolution. However, the SVF and temperature vary little over the central 3 mm of our flame at the 42 mm height so the loss of spatial resolution is not important.

The collected radiation exciting from the receiver aperture is collimated with a Thor Labs BPX055 25-mm-diameter, 35-mm focal length lens, and the collimated radiation is incident at 15° on a Semrock Razor-Edge Long Wave Pass Filter, LP02-488RS-25, with a reflectivity of at least 95 % at 450 nm and transmission of at least 95 % above 490 nm. The reflected light is passed through a 25-mm-diameter Semrock bandpass filter, FF02-447/60-25. This bandpass filter has a centre wavelength near 445 nm with a 60-nm FWHM and a peak transmission of approximately 95 %. The radiation is then focussed on the photocathode of a Hamamatsu H5783-03 bialkali photomultiplier module (SN833-5384) using a plano-convex 50-mm anti-reflection coated lens producing an image of approximately 4 mm diameter. The photomultiplier was directly connected to a Femto model HCA-400 M-5 K-C high-speed current amplifier with a gain of 5000 V/A. For the higher wavelength channel, the radiation passing through the first dichroic is incident at 15° on a CVI dichroic beam splitter, LWP-0-R790-T1064-PW-1012-C and is reflected on to a Semrock FF01-750/50-25.4 bandpass filter at 750 nm with a FHWM bandpass of 50 nm. The photomultiplier module in the high wavelength channel was a Hamamatsu H5783-20; otherwise, the components were the same as the low wavelength channel.

To calculate the centre wavelength and the equivalent width of each detection channel, it is not sufficient to use the characteristics of the final interference filter. Rather, one must integrate the detector response to the light source as modulated by the dichroic, the interference filter and the photocathode response of the photomultiplier over a wavelength band as described in [8]. Following this procedure, we obtained a centre wavelength of 445.1 nm with an equivalent width bandpass of 60.9 nm for the lower wavelength channel and 750.1 nm and an equivalent width bandpass of 54.6 nm for the upper wavelength channel. In calculating the integrated light throughput, the detection channel can then be simulated by calculating the intensity of the light source at the centre wavelength of the equivalent filter and multiplying by the filter equivalent width [8].

The source of excitation was a Newport model LQA808-170C diode laser operating at 804.1 nm with a maximum CW power output of 175 mW. A Newport model LPMS-5-110 power supply was used to drive the laser diode. This power supply was in turn controlled by a Tektronix AFG3022B Function Generator which allowed sine wave modulation of the laser diode output. The beam parameters measured with a BeamView camera at distance of 640 mm from the laser exit port (the location of the MLII collection volume) gave a 1/e 2 diameter of 1.44 mm. The laser power output was recorded using a Scientech model AC2501-H volume absorbing 25-mm-diameter disc calorimeter attached to a Scientech model S310D display unit. A Thor Labs model DET36A silicon detector equipped with a model 800/12 Semrock BrightLine interference filter was used to record the modulated 804.1 nm light signal. The output temporal profile of the laser was recorded on an oscilloscope and found to be a sinusoidal at all frequencies.

Two types of lock-in amplifiers were used in this work. Initially, a pair of Femto LIA-MV-150-S lock-in amplifiers was used to monitor the modulated LII signal from the Femto model HCA-400 M-5 K-C high-speed current amplifiers. The Femto lock-in amplifiers were single channel and limited to an upper frequency of 40 kHz. For each channel, the phase of the Femto lock-in, with respect to the laser signal that was used as the reference, was adjusted and the resulting signal amplitude recorded. The fit function, f, is of the form \(f(\theta ,u) = u_{1} \times \cos (\theta - u_{2} ) + u_{3}\) where u1 is the AC signal amplitude, u3 is the amplifier DC offset, and u 2 is related to the phase delay of the AC signal from the laser excitation source. In these experiments, a TTL logic pulse from the sine wave generator, which controlled the laser, was used to trigger the lock-in amplifier reference channel. This TTL logic pulse bore a constant phase relationship to the laser excitation source whose phase we measured separately to get the final phase delay. The phase angle and 95 % confidence limits were −56.82° ± 0.36° 750-nm channel and −55.99 ± 0.59 450-nm channel. The 95 % confidence limit amplitude errors were 0.6 % for the 750 nm and 1.0 % for the 445 nm channel. In order to extend the frequency range of the measurements to 200 kHz, an Ametek model 7265 lock-in amplifier was used. The Ametek was a two channel unit that allowed both photomultipliers to be monitored simultaneously, and it automatically determined the amplitude of the modulated signals of both channels and the phase delay with respect to the modulated laser signal which triggered the lock-in. The laser modulation frequency was adjustable from 10 Hz to 200 kHz.

In the interpretation and discussion of the present measurements, data acquired using a 2D line-of-sight attenuation (2D-LOSA) method will be used. Details of the apparatus, where a mercury arc lamp is used as the light source, can be found in [9]. In addition to the 577 nm data presented in [9], additional unpublished data acquired at 436 and 825 nm using the same apparatus are presented here. For the 436 nm attenuation measurements, a 436DF20 interference filter (Omega Optical) with 20 nm bandwidth was used in place of the 577DF20 577-nm filter. For the 825 nm measurements, a 825DF50 filter with 50 nm bandwidth was used. Three separate experiments were performed for each wavelength over a period of 3 months to assess the repeatability of the measurements.

The burner for generating the laminar coflow ethylene diffusion flame at atmospheric pressure used in the present study was previously described in detail [10]. Briefly, the burner consists of a central fuel tube with a 10.9 mm inner diameter surrounded by an annular air nozzle of 88 mm inner diameter. The ethylene flow rate was 3.23 cm3/s (21 °C, 1 atm), and the air flow rate was 4.73 L/s, resulting in a visible flame height of about 64 mm. The present MLII experiments were carried out at a height of 42 mm above the burner exit and on the burner centreline where the soot concentration is essentially constant over the central 3 mm of the flame.

3 Theory of modulated LII

The theory can be divided into two parts: the derivation of soot temperatures from the ratio of the calibrated 445 and 750 nm modulated emission detection and derivation of the equations describing the MLII signal and its phase with relation to the excitation source.

3.1 Soot temperature

The derivation of soot temperature from calibrated LII signals has been well described previously, for example [8], and will only briefly be covered here. The ratio of the soot incandescence, P p, at the two temperatures is given by:

$$\frac{{P_{\text{p}} (\lambda_{1} )}}{{P_{\text{p}} (\lambda_{2} )}} = \frac{{\lambda_{2}^{6} E(m_{{\lambda_{1} }} )}}{{\lambda_{1}^{6} E(m_{{\lambda_{2} }} )}}\exp \left[ { - \frac{hc}{{kT_{\text{s}} }}\left( {\frac{1}{{\lambda_{1} }} - \frac{1}{{\lambda_{2} }}} \right)} \right]$$
(1)

where λ 1 is the lower detection wavelength and λ 2 is the upper detection wavelength, c is the speed of light, h the Planck constant, and k the Boltzmann constant. T s is the soot temperature, and E(m λ ) is the soot absorption coefficient for refractive index m λ . Following our earlier work [11], we have assumed E(m λ ), to be independent of wavelength. This assumption is consistent with the results of Coderre et al. [12], whilst Migliorini et al. [13] found a small increase to blue wavelengths, and Krishnan et al. [14] found a small increase towards red and near IR wavelengths. The calibration of the two detection channels was performed with a calibrated integrating sphere light source rather than a strip filament lamp and has been described in detail previously [8, 11]. We have ratioed the amplitude of the MLII signals at the two wavelengths to obtain soot temperature using Eq. 1.

The modulated soot temperature will necessarily be higher than the undisturbed (DC) soot temperature; however, we show in Sect. 4.3 that the estimated temperature increase is approximately 3.8 K at 10 Hz declining to 0.2 K at 100 kHz.

3.2 Modulated LII signal and its phase

The absorption of laser radiation of power density P d (power/unit area) and wavelength λ by a single soot primary particle of diameter d p is given by the product of P d and the particle optical absorption cross section, which is in turn given by the product of the particle physical cross section \(\frac{{\pi d_{\text{p}}^{2} }}{4}\) and its absorption efficiency \(\frac{{4\pi E(m_{\lambda } ) d_{\text{p}} }}{\lambda }\) [15]. The concentration of primary particles, N pp, is given by \(N_{\text{pp}} = \frac{{6 f_{\text{v}} }}{{\pi dp^{3} }}\) where f v is the SVF.

The laser heating of the soot (power per unit volume) of soot laden air, P vol, is then given by:

$$P_{\text{vol}} = P_{\text{d}} \frac{{6 \pi E\left( {m_{\lambda } } \right) f_{\text{v}} }}{\lambda }$$
(2)

Although the laser radiation is initially absorbed by the soot particles, rapid cooling of the soot by the surrounding gas will result in gas heating. To apportion this heating, we need to take account of the heat capacity of both the soot and the gas. The volumetric heat capacity of the soot per unit volume of soot/air mixture, HCsoot, is given by:

$${\text{HC}}_{\text{soot}} = \rho_{\text{soot}}f_{\text{V}} C_{{{\text{P}}_{\text{soot}} }}$$
(3)

where ρ soot is the soot density and \(C_{{{\text{P}}_{\text{soot}} }}\) is the soot heat capacity per unit mass. If we define HCair as the volumetric heat capacity of air, the ratio of the soot and air heat capacities, R HC, is given by \(R_{\text{HC}} = \frac{{ {\text{HC}}_{\text{soot}} }}{{{\text{HC}}_{\text{air}} }}\).

The soot heating term is given by:

$$\frac{{{\text{d}}T_{\text{s}} }}{{{\text{d}}t}} = \frac{{P_{0} }}{2}\left( {1 + \sin \left( {\omega t} \right)} \right) \frac{{6 \pi E(m_{\lambda } )}}{{\lambda \rho_{\text{soot}} C_{{{\text{p}}_{\text{soot}} }} }}$$
(4)

where we have replaced P d by the modulated laser power \(\frac{{P_{0} }}{2}(1 + \sin (\omega t)),\) where P 0 is the peak power density of the laser and \(\omega\) is the angular frequency of the laser 2πf.

We can now set up equations for the laser heating of the particle laden gas by making the approximation that the soot and gas temperatures within the laser irradiation sample volume can be represented by averages. This is important since the profile of the laser is Gaussian, so in fact there will be temperature gradients in the laser-illuminated region. However, unlike pulsed LII the temperature excursions with illumination in MLII are very small and are essentially linear in laser power. In addition, the variation of radiation intensity is also essentially linear with temperature as demonstrated in Sect. 4.3. In these circumstances replacing a spatially varying temperature by an average temperature should be an acceptable approximation. The differential temperature describing the soot heating can be cast as:

$$\frac{{{\text{d}}T_{\text{s}} }}{{{\text{d}}t}} = \psi \left( {1 + \sin \left( {\omega t} \right) } \right) - \frac{{\left( {T_{\text{s}} - T_{0} } \right)}}{{\tau_{\text{g}} }} - \frac{{\left( {T_{\text{s}} - T_{\text{g}} } \right)}}{{\tau_{\text{s}} }}$$
(5)

where the constant terms not dependent on \(\omega t\) in Eq. 4 have been replaced by \(\psi\), T s and T g are, respectively, the soot and gas temperature in the illuminated sample volume and T 0 is the unperturbed gas and soot temperature. τ g is the time constant for gas replacement in the sample volume or, alternatively, the residence time of the soot particle and τ s is the soot cooling rate time constant. A second differential equation can be written for T g:

$$\frac{{{\text{d}}T_{\text{g}} }}{{{\text{d}}t}} = R_{\text{HC}} \frac{{\left( {T_{\text{s}} - T_{\text{g}} } \right)}}{{\tau_{\text{s}} }} - \frac{{\left( {T_{\text{g}} - T_{0} } \right)}}{{\tau_{\text{g}} }}$$
(6)

Here, we use the heat capacity ratio to describe the amount of gas heating resulting from the soot cooling.

Subtracting Eq. 6 from Eq. 5 and rearranging, we get:

$$\frac{{{\text{d}}\left( {T_{\text{s}} - T_{\text{g}} } \right)}}{{{\text{d}}t}} + \left( {T_{\text{s}} - T_{\text{g}} } \right)\left[ {\frac{{1 + R_{\text{HC}} }}{{\tau_{\text{s}} }} + \frac{1}{{\tau_{\text{g}} }}} \right] = \psi \left( {1 + \sin \left( {\omega t} \right)} \right)$$
(7)

Equation 7 can be solved for T s − T g by multiplying both sides by the integrating factor \({ \exp }\left\{ {t\left( {\frac{{1 + R_{\text{HC}} }}{{\tau_{\text{s}} }} + \frac{1}{{\tau_{\text{g}} }}} \right)} \right\}\) when the left-hand side of Eq. 7 becomes a perfect differential

$$\frac{\text{d}}{{{\text{d}}t}}\left[ {\exp \left\{ {t\left( {\frac{{1 + R_{\text{HC}} }}{{\tau_{\text{s}} }} + \frac{1}{{\tau_{\text{g}} }}} \right)} \right\}\left( {T_{\text{s}} - T_{\text{g}} } \right)} \right]$$

And the right-hand side becomes \(\psi (1 + \sin (\omega t))\exp \left[ {t\left( {\frac{{1 + R_{\text{HC}} }}{{\tau_{\text{s}} }} + \frac{1}{{\tau_{\text{g}} }}} \right)} \right].\)

To avoid future complex expressions, we define \(C_{\text{n}} = \frac{{1 + R_{\text{HC}} }}{{\tau_{\text{s}} }} + \frac{1}{{\tau_{\text{g}} }}\). Integrating the left-hand side of Eq. 7, we get \(\exp \{ t C_{\text{n}} \} (T_{\text{s}} - T_{\text{g}} )\) and the integral of the right-hand side is:

$$\int {\psi \left( {1 + \sin \left( {\omega t} \right)} \right)\exp \left[ {t C_{\text{n}} } \right]}$$
(8)

This integral is given by:

$$\frac{{\psi \exp \left( {C_{\text{n}} t} \right)\left[ {C_{\text{n}}^{2} + \omega^{2} + C_{\text{n}}^{2} \sin (\omega t) - C_{n} \omega \cos (\omega t)} \right]}}{{C_{\text{n}}^{3} + C_{\text{n}} \omega^{2} }}$$
(9)

We can equate the integrals of the two sides of the equation eliminating the common \(\exp (C_{\text{n}} t)\) term to get:

$$T_{\text{s}} - T_{\text{g}} = \frac{{\psi \left[ {C_{\text{n}}^{2} + \omega^{2} + C_{\text{n}}^{2} \sin (\omega t) - C_{\text{n}} \omega \cos (\omega t)} \right]}}{{C_{\text{n}}^{3} + C_{\text{n}} \omega^{2} }}$$
(10)

where we have ignored the constant of integration. We are not modelling the transient behaviour of temperature at the start of the laser modulation where T s = T g at t = 0, but rather the steady state behaviour when modulation is well established. Here, t = 0 (arbitrarily) corresponds to the start of the laser heating cycle and, in the steady state, T s − T g is constant for t = 0 ± m × 2π/f where m is the number of sine wave cycles after t = 0. We cannot know the value of T s − T g at t = 0 ± m × 2π/f until we solve the equations.

Equation 10 can be simplified by defining a phase angle \(\tan (\phi ) = \frac{\omega }{{C_{\text{n}} }} = \frac{\omega }{{\frac{{1 + R_{\text{HC}} }}{{\tau_{\text{s}} }} + \frac{1}{{\tau_{\text{g}} }}}}.\) Substituting the phase angle for C n in Eq. 10 and simplifying we get the following expression for T s − T g:

$$T_{\text{s}} - T_{\text{g}} = \frac{\psi \tan (\phi )}{\omega }\left\{ {1 + \cos (\phi )\sin \left[ {\omega t - \phi } \right]} \right\}$$
(11)

This equation is similar in form to the classic equation for obtaining fluorescence lifetime by measuring the phase delay of the fluorescence with respect to the exciting laser where the ϕ in \(\sin (\omega t - \phi )\) represents the phase delay and the cos(ϕ) term the reduction in fluorescence intensity that results with increasing phase delay.

We must now solve the equation for T g. If we substitute our solution for T s − T g from Eq. 11 into Eq. 5 and rearrange the equation to have the T g terms on the left, we get:

$$\frac{\text{d}}{{{\text{d}}t}}T_{\text{g}} + \frac{{T_{\text{g}} }}{{\tau_{\text{g}} }} = \frac{{R_{\text{HC}} \psi \tan (\phi )\left[ {1 + \cos (\phi )\left( {\sin \left( {\omega t - \phi } \right)} \right)} \right]}}{{\omega \tau_{\text{s}} }} + \frac{{T_{0} }}{{\tau_{\text{g}} }}$$
(12)

We can integrate this equation by multiplying both sides by the integrating factor \(\exp \left( {\frac{t}{{\tau_{\text{g}} }}} \right)\) when the left-hand side becomes an exact differential \(\frac{\text{d}}{{{\text{d}}t}}\left[ {T_{\text{g}} \exp \left( {\frac{t}{{\tau_{\text{g}} }}} \right)} \right]\) which is readily integrated to give \(T_{\text{g}} \exp \left( {\frac{t}{{\tau_{\text{g}} }}} \right).\) The right-hand side integral is:

$$\int {\exp \left( {\frac{t}{{\tau_{\text{g}} }}} \right)\left[ {\frac{{T_{0} }}{{\tau_{\text{g}} }} + \frac{{R_{\text{HC}} \psi \tan \left( \phi \right)\left[ {1 + \cos \left( \phi \right)\left( {\sin \left( {\omega t - \phi } \right)} \right)} \right]}}{{\omega \tau_{\text{s}} }}} \right]}$$
(13)

Integrating Eq. 13 and equating it to the integral of the left-hand side and simplifying leads to the following equation for T g:

$$\begin{aligned} T_{\text{g}} & = T_{0} + \frac{{R_{\text{HC}} \psi \tan \left( \phi \right)\tau_{g} }}{{\omega \tau_{\text{s}} \left( {\omega^{2} \tau_{\text{g}}^{2} + 1} \right)}}\left[ {\cos \left( \phi \right)\sin \left( {\omega t - \phi } \right) + \left( {\omega \tau_{\text{g}} } \right)^{2} } \right. \\ & \quad \left. { + \,\omega \tau_{\text{g}} \left\{ {\sin \left( {\phi - \frac{\omega t}{2}} \right)^{2} + \sin \left( {\frac{\omega t}{2}} \right)^{2} - 1} \right\} + 1} \right] \\ \end{aligned}$$
(14)

where again we have ignored the constant of integration.

We can now get a solution for the soot temperature T s by adding Eqs. 10 and 14:

$$\begin{aligned} T_{\text{s}} & = T_{0} + \frac{\psi \tan(\phi)}{\omega}\left[{1 + \cos (\phi)(\sin (\omega t - \phi))} \right. \\ & \quad + \frac{{R_{\text{HC}} \tau_{\text{g}}}}{{\tau_{\text{c}} \left({\left({\omega \tau_{\text{g}}} \right)^{2 } + 1} \right)}}\left\{{\cos \omega (\phi)\sin (\omega t - \phi) + (\omega \tau_{\text{g}})^{2}} \right. \\& \left. {\quad \left. {+ \omega \tau_{\text{g}} \left\{{\sin \left({\phi - \frac{\omega t}{2}} \right)^{2} + \sin \left({\frac{\omega t}{2}} \right)^{2} - 1} \right\} + 1} \right\}} \right] \\ \end{aligned}$$
(15)

We have eliminated the variable T g by subtraction and this can be taken as justification for ignoring the integration constant for the two expressions for T g Eqs. (10) and (14).

This equation describes the soot temperature as the undisturbed soot temperature T 0, plus some complex function of time. To interpret the experimental phase delays, we would like to know the phase relationship of the time varying part of Eq. 15 relative to that of the laser excitation function, \(1 + \sin (\omega t).\) The phase delay is not obvious from Eq. 15, but if we take the first derivative of T s with respect to time, we can more readily find the maxima and minima where the derivative is zero. Taking the derivative of Eq. 15 with respect to time and simplifying, we get:

$$\begin{aligned} \frac{\text{d}}{{{\text{d}}t}}T_{\text{s}} & = \frac{\psi \sin (\phi )}{{\tau_{\text{s}} \left( {\omega \tau_{\text{g}} } \right)^{2} + \tau_{\text{s}} }}\left[ {\omega R_{\text{HC}} \tau_{\text{g}}^{2} \sin \left( {\omega t - \phi } \right)} \right. \\ & \quad \left. { + \left( {\tau_{\text{s}} \left( {\omega \tau_{\text{g}} } \right)^{2} + R_{\text{HC}} \tau_{\text{g}} + \tau_{\text{s}} } \right)\cos (\phi ) \cos (\phi - \omega t)} \right] \\ \end{aligned}$$
(16)

By setting the differential \(\frac{\text{d}}{{{\text{d}}t}}T_{\text{s}} = 0\), we can solve for the \(\omega t\) value or the phase value ϕ 0 for which the differential is zero:

$$\phi_{0} = {\text{atan}}\left( {\frac{\omega }{{\frac{{1 + R_{\text{HC}} }}{{\tau_{\text{s}} }} + \frac{1}{{\tau_{\text{g}} }}}}} \right) - {\text{atan}}\left( {\frac{{\tau_{\text{s}} \left( {\omega \tau_{\text{g}} } \right)^{2} + R_{\text{HC}} \tau_{\text{g}} + \tau_{\text{s}} }}{{\omega R_{\text{HC}} \tau_{\text{g}}^{2} }}} \right).$$
(17)

By calculating numeric values of the second differential, we can determine whether turning point given by Eq. 17 is a maximum or a minimum. The second derivative of the soot temperature with respect to time is given by:

$$\begin{aligned} \frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }}T_{\text{s}} & = \frac{\psi \sin (\phi )}{{\tau_{\text{c}} \left( {1 + \left( {\omega \tau_{\text{g}} } \right)^{2} } \right)}}\left[ {R_{\text{HC}} \left( {\omega \tau_{\text{g}} } \right)^{2} \cos (\phi - \omega t)} \right. \\ & \left. {\quad + \sin (\phi - \omega t) \omega \left( {\tau_{\text{s}} \left( {\tau_{\text{g}} \omega } \right)^{2} + R_{\text{HC}} \tau_{\text{g}} + \tau_{\text{s}} } \right)} \right] \\ \end{aligned}$$
(18)

From numeric values of the second derivative at ωt values given by ϕ 0 in Eq. 17, we find that the second derivative is positive, indicating that ϕ 0 represents a minimum.

To undertake these numerical evaluations, we initially used estimates of the parameters τ s, τ g and R HC (for which we need to know the SVF). A magnitude for the laser heating term, ψ, is not required at this point because it is a multiplier in both Eqs. 16 and 18 and does not affect the functional values for which Eq. 16 becomes zero or the sign of the second differential in Eq. 18. The flow velocity on centreline in the laminar diffusion flame [16] was approximately 190 cm/s and the laser beam 1/e 2 diameter of 1.4 mm giving a gas transit time of ~75 ms. The SVF was taken as 2.5 ppm and τ s as 1.23 μs (Table 1).

Table 1 Best-fit values and 95 % confidence limits (CL) for fit to phase data using Eq. 17
Full size table

Using these numerical estimates, ϕ 0 in Eq. 17 can be shown to be negative and to be a minimum occurring between phase angle 0 and −π/2. The phase maxima will be ±π from ϕ 0. The laser excitation source, \(\psi (1 + \sin (\omega t)),\) has its first maximum at ωt = π/2, so the phase delay of the MLII signal with respect to the laser source is given by \(\phi_{0} + \pi - \frac{\pi }{2} = \phi_{0} + \frac{\pi }{2}.\)

The phase of the signal is measured from the modulated radiation signal not the temperature directly, so we need an expression for the modulated radiation signal in terms of the modulated temperature. The blackbody power, \(P_{\text{p}} (\lambda ),\) emitted by particle into 4 × π steradians per unit wavelength interval is [15]:

$$P_{\text{p}} \left( \lambda \right) = \frac{{8 \pi^{3} c^{2} h}}{{\lambda^{6} }}\left( {\exp \left( {\frac{h c}{\lambda kT}} \right) - 1} \right)^{ - 1} d_{\text{p}}^{3} E\left( {m_{\lambda } } \right)$$
(19)

4 Results and discussion

4.1 Soot temperature measurements

The temperature measurements taken with both lock-in amplifiers are shown in Fig. 2, and the average of all measurements and single standard deviation were 1706 ± 14 K. This error is the precision of the measurement and does not reflect systematic uncertainties such as the relative value of E(m λ ) and any relative calibration errors. The image size at the centre of the flame is a circle of diameter 2 mm, so we are averaging the temperature measurements over the radial range r = 0–1 mm. The CARS temperature measurements in a similar burner and with identical air, and fuel flow rates averaged over this radial range were [10] 1681 ± 25 K.

In analysing our MLII data, and in previous work [11, 17], we have assumed a constant E(m λ ) independent of wavelength. Our choice was based on the work of Coderre et al. [12] and on previously unpublished data that we present here. Migliorini et al. [13] have shown an E(m λ ) value in the visible and near IR that is largely flat, but rises somewhat at lower wavelengths, whilst Krishnan et al. [14] found similar behaviour, but with a rise in small E(m λ ) to near IR wavelengths.

The agreement between the MLII temperature of 1706 K and the CARS temperature of 1681 ± 25 K supports our choice of a wavelength independent E(m λ ).

Fig. 2
figure 2

Soot temperature as a function of laser modulation frequency. Open diamonds 2013/09/18 Ametek with line filter, open circles 2013/09/30 Ametek without line filter, open triangles 2013/09/30 Ametek with line filter

Full size image

4.2 Lock-in amplifier phase measurements and their interpretation

The measured phase angle (average of 445 and 750 nm values) and the fit to the theoretical expression in Eq. 17 are shown in Fig. 3. The fitting function used was Mathcad’s least-squares fit function which provides best-fit values and confidence limits. The resulting best-fit values and 95 % confidence limits resulting from the fit in Fig. 3 are shown in Table 1. The mean values were as follows: SVF 2.29 ppm, cooling rate time constant, 1.23 μs and flow residence time 0.46 ms. The overall fit to the data is good although the low frequency phase delay peak at ~1050 Hz is underestimated by approximately 10 %. Almost no difference to the best-fit values or the confidence limits was observed when the 10 Hz data were removed. The poor fit of the 10 Hz data may be attributable to flame fluctuations which could be important at these very low frequencies. The quality of fit is highly satisfactory given the wide range of frequencies employed.

Fig. 3
figure 3

Measured phase delay of MLII signals with respect to laser excitation source. Open squares and open circles are the phase data from 445- to 750-nm channels, respectively, using 7265 lock-in amplifier. Open triangle, and open diamond are the phase data from 445- to 750-nm channels, respectively, using Femto lock-in amplifier. Curve least-mean-squares fit of data to Eq. 17

Full size image

The 95 % confidence limits are quite low, in the range 3.6–5.6 % of the mean values, with the cooling rate time constant being most accurately determined and the SVF the least. Of course these errors do not include any systematic errors in assumed properties, but the soot density is well established at 1.89 ± 0.09 (95 % confidence limit) from the data listed in Dobbins et al. [18] and, provided the heat capacity of graphite is a good surrogate for soot, these errors should be small.

Unlike most other optical flame measurements the SVF determination does not depend on knowing soot optical properties, but, instead, depends on knowing the heat capacity of soot. Graphite is believed to be a fairly good surrogate for soot for heat capacity, and this assumption is made here. The soot cooling time constant is compared with Snelling et al. [17] who gave an Eq. (12) for \(\frac{{{\text{d}}\,\ln (T - T_{\text{g}} )}}{t}\), the temporal decay of the difference between the soot and gas temperature. This equation is readily integrated to give an exponential decay expression for the temperature difference from which the time constant of the cooling, τ, can readily be derived as:

$$\tau = \frac{{2f\lambda_{{{\text{MFP}} }} \rho_{\text{s}} c_{\text{s}} d_{\text{p}} N_{\text{p}} }}{{3 \alpha k_{a} \left( {\gamma + 1} \right)}}\left( {\frac{fa}{{N_{\text{p}} }}} \right)^{{\frac{1}{{\varepsilon_{a} }}}}$$
(20)

The original paper should be consulted for details, but we list here the meaning of the symbols and their value at 42 mm height in the laminar diffusion flame taken from [17]: f = 1.656 is the Eucken factor, \(\lambda_{\text{MFP}} = 603 \,{\text{nm}}\) is the mean free path in the gas, ρ s = 1.9 gm/cm2 is the soot, c s = 2100 J/kg K is the soot specific heat, α is the accommodation coefficient, k a = 0.11 J/m s K is the heat conduction coefficient of the gas, N p = 42 is the mean number of primary particles in a soot aggregate, γ = 1.291 is the specific heat ratio of the gas, and f a = 1.1 and ε a = 1.08 are scaling factors taken from Brasil et al. [19] that relate the effective area of the aggregate to N p and d p. We can readily rearrange Eq. 20 to express the only unknown, α, in terms of the other parameters, and using our measured time constant of 1.29 μs we get α = 0.35.

In Fig. 9 of [17], the derivation of α gave α = 0.37 for d p = 29 nm over the temperature decay range 2900–2200 K. This is very close to our present value of 0.35 measured at 1700 K. Whilst the difference is probably within the combined uncertainty limits of the two measurements, the accommodation coefficient is expected to change with temperature, and Michelsen [20] has shown from compiling data on NO that the accommodation coefficient for NO drops with decreasing gas temperature.

The axial flow velocity in the laminar diffusion flame at the 42 mm height is ~190 cm/s [16], and if we take the laser beam 1/e 2 diameter of 1.435 mm as a measure of the sample size in the axial direction, we get a residence time of 0.76 ms, which is considerably more than our measured 0.47 ms. We previously estimated self-diffusion in the laminar diffusion flame at the 42 mm height using simple hard sphere collision theory and the equation x 2 = 2Dt where x is the distance diffused in time t and D is the self-diffusion coefficient [11], and using this hard sphere data we get D = 3.6 × 10−4 m2 s−1. Thus, in the measured 0.46 s the self-diffusion distance is 0.58 mm, which is appreciable compared to the sample dimensions. Such diffusion will not only occur axially, but in a direction orthogonal to this and to the laser excitation axis. It seems likely the gas replacement time is not only controlled by bulk flow but also by self-diffusion. Had we wished to measure axial gas flow more accurately, it would have been beneficial to transform the circular laser beam into a laser sheet with the long axis orthogonal to the burner axis. The smaller dimension in the vertical direction would have reduced the time constant and made the flow orthogonal to this axis of less significance because of the larger beam size in that direction.

4.3 Signal amplitude

Equation 15 gives the soot temperature from which we have derived the theoretical phase delays. In deriving the experimental phase from the radiation signal and comparing it to theory, we are implicitly assuming a linear relationship between intensity modulation and temperature modulation, i.e. that the temperature modulation is sufficiently small. We can readily calculate the amplitude of the modulated LII (MLII) signal by noting that, as derived above, a minimum in the temperature curve occurs for an ωt value of φ 0 (Eq. 17) and of course the maximum will occur at ωt = φ 0 + π. After substituting these values for ωt in Eq. 15 and subtracting T s,min from T s,max and some simplification, we obtain an expression for the amplitude of the modulated soot temperature, ΔT amp.

$$\Delta T_{\text{amp}} = \frac{\psi \tan (\phi ) 2 \cos (\phi )}{{\omega \tau_{\text{s}} }}\left[ {\frac{{\left( {\omega \tau_{\text{g}} \tau_{\text{s}} } \right)^{2} + \left( {Hr\tau_{\text{g}} } \right)^{2} + 2Hr\tau_{\text{s}} \tau_{\text{g}} + \tau_{{{\text{s}} }}^{2} }}{{(\omega \tau_{\text{g}} )^{2 } + 1}}} \right]^{0.5}$$
(21)

In Fig. 4, we use this expression to compare the relative amplitudes of the experimental modulated LII signals at 445 and 750 nm to theory. The average signal of the 750-nm channel is 57.1 times that of the 445-nm channel, and it has been normalised accordingly in Fig. 4. The amplitude Eq. 21 is not a function of laser time, as expected, and the scaled relative intensities of the two channels are indistinguishable. The theory provides a satisfactory fit to the experimental amplitude data.

Fig. 4
figure 4

Relative amplitude of modulated LLI signal amplitude compared to theory using best-fit parameters from phase fit in Table 1

Full size image

In principle, the unknowns, τ s, τ g and R HC can be obtained from applying the least-mean-squares fitting function to the amplitude Eq. (21) rather than the phase function (17). In fitting the amplitude function, we have the additional uncertainty of the absolute value of the radiation signal, which requires an additional fitting parameter for the signal scaling function. We have attempted such a fit and found values of the fit parameters consistent with those obtained from fitting the phase function, but with very large error limits, for example, a SVF mean and single standard deviation of 1.7 ± 0.8.

At moderate and low frequencies, the laser modulation period is sufficiently long that the soot cooling term dominates and both the gas and soot temperatures are essentially identical. At the higher frequencies, the soot increasingly does not come to equilibrium with the gas and the modulated laser heating resides more in the soot. The rise in amplitude with lower frequency results from the fact that with heating of both the soot and the gas the relevant time constant is the gas replacement time and very much more laser energy can be deposited with decreasing frequency. Finally, a point is reached where the excitation frequency is so low that negligible gas replacement occurs during a single period of the laser oscillation. With further reduction in frequency, no further increase in amplitude is possible.

We can also use Eq. 21 to estimate the absolute modulated soot temperature amplitudes. We have defined ψ above as \(\psi = \frac{{P_{0} }}{2} \frac{{6 \pi E(m_{\lambda } )}}{{\lambda \rho_{\text{soot}} c_{\text{psoot}} }}\). We will assume that all of the available laser energy was in the fundamental frequency, and taking the laser beam 1/e 2 diameter of 1.435 mm as a measure of the sample size and with a laser power is 150 mW gives us a power density, P 0, of 92 mW/mm2. The laser wavelength is 804.1 nm; taking E(m λ ) = 0.4, ρ soot = 1.89 gm/cm2, c psoot = 2030 J/kg K then ψ = 1.13 × 105 K/s. Using our best-fit values for τ soot, τ gas and f v and 0.4 for E(m λ ) at the laser wavelength of 804 nm, we estimate peak modulated soot temperature amplitudes of 3.80, 1.24 and 0.22 K at frequencies of 10, 103 and 106 Hz, respectively. Thus, it is concluded that the highest estimated soot modulation temperatures do not significantly perturb the soot temperature.

In Fig. 5, the dependence of soot radiation intensity on temperature is shown for the range T = 1710–1720 K using Eq. 19. Over this 10 K range there is a near linear relationship between temperature change and radiation although the 455-nm channel departs very slightly from a linear relationship. This relationship ensures that phase delays derived from soot radiation intensities will match those expected from soot temperature theory over the maximum temperature modulation of 3.8 K expected in these measurements.

Fig. 5
figure 5

Power emitted by a single primary particle into 4π steradians per unit wavelength interval. Solid line 750 nm, dotted line 445 nm

Full size image

4.4 Determination of E(m λ ) using MLII and 2D-LOSA

As has been demonstrated in Sect. 4.3, phase analysis of MLII allows an optical method to measure SVF which is not dependent on knowledge of the optical properties of soot. This represents a unique opportunity to make an evaluation of the optical properties of flame soot when MLII determined SVF is combined with other optical techniques that measure local soot absorption coefficients. The absorption is a function of the product of SVF and the soot absorption function. To derive soot optical properties, we need to know the SVF independently and since in flame gravimetric sampling is not feasible the modulated LII derivation of SVF gives us the unique opportunity to derive in flame E(m) measurements from our previously performed soot absorption measurements in the same flame and location.

We have previously published part of a study of Abel inversion of 2D line-of-sight attenuation (2D-LOSA) measurements in an identical laminar diffusion flame [9]. In addition to the published 577 nm data, measurements were acquired at 436 and 825 nm but not published. The local extinction coefficient \(K_{{{\text{ext}}\lambda }}\) resulting from the Abel inversion of the line-of-sight attenuation data [9] is shown in Fig. 6. Three separate experiments were performed over period of 3 months to assess the repeatability of the measurements, and these are shown using different plotting symbols in Fig. 6. The inversion was performed every 0.1 mm, but the points are shown in only one of the three curves at each wavelength for clarity. The local extinction coefficient relates to the SVF through the relationship \(f_{\text{v}} = \frac{{K_{{{\text{ext}}\lambda }} \lambda }}{{6 \pi (1 + \rho_{{{\text{sa}}\lambda }} )E(m_{\lambda } )}}\) where \(\rho_{\text{sa}}\) is the ratio of scattering coefficient to absorption coefficient, \(\rho_{{{\text{sa}}\lambda }} = \frac{{K_{{{\text{sca}}\lambda }} }}{{K_{{{\text{abs}}\lambda }} }} .\)

Fig. 6
figure 6

Local soot extinction measurements at 42 mm height in laminar diffusion flame at three different wavelengths 465 nm in blue, 577 nm in green and 825 nm in red

Full size image

\(\rho_{\text{sa}}\) can be determined numerically from Rayleigh–Debye–Gans (RDG) theory using the approach of Sorensen [21]. Detailed calculations have been presented previously for the measurement location of 42 mm height in the Gulder flame at a wavelength of 532 nm [22]. The input data were an analysis of a large (4695) aggregate sample taken at the centre line of the laminar diffusion flame during three measurement campaigns. The fractal parameters for the equation \(N = k_{\text{f}} \left( {\frac{{2R_{\text{g}} }}{{{\text{d}}p}}} \right)^{{D_{\text{f}} }}\) where N is the number of primary particles in the aggregate, k f the fractal prefactor, D f the fractal dimension and R g the radius of gyration. A fit to the data gave k f = 2.05 and D f = 1.704. The aggregate size distribution was fitted to a lognormal distribution over the whole range N = 4–500 and to both lognormal and self-preserving distributions over the reduced range N = 20–500 since scattering is dominated by the high-N part of the aggregate size distribution [21]. More details including the aggregate fits and the RDG complex hypergeometric scattering implementation can be found in Snelling et al. [22]. Values for F(m λ )/E(m λ ), the ratio of the scattering and absorption functions, were taken from Krishnan et al. [14] who summarised the available measurements, Values of 0.814, 1.22 and 1.55 were estimated from a rather crude log–log plot for wavelengths of 436, 577 and 825 nm, respectively. Using these F(m λ )/E(m λ ), values, \(\rho_{{{\text{sa}}\lambda }}\) was calculated for the full range lognormal (N g = 19.0, σ g = 3.70), the high-end lognormal (N g = 30.0, σ g = 2.87) and the high-end self-preserving fit (N mean = 29.9, τ = 0.60) to the aggregate data. The results are given in Table 2 where it can be seen that the full range lognormal gave the highest values of \(\rho_{{{\text{sa}}\lambda }}\) and the high-N self-preserving the lowest, these two sets differing by ~15 %. Yet different values would have been derived if we had limited the aggregate size fit to N < 300, which is the common upper limit when only 300–500 aggregates are analysed. The problem results from the fact that no single set of lognormal parameters provides a good fit to the whole N range [22]. Since numerical simulation of aggregating systems has shown that, after a short delay, the diffusion limited aggregating systems follow a self-preserving scaling distribution [23–26] rather than a lognormal distribution, and since Sorensen has shown the high-N self-preserving limit to be adequate to describe scattering [21], we will use these values of to correct our extinction measurements.

Table 2 \(\rho_{{{\text{sa}}\lambda }}\) values calculated from RDG scattering to TEM-derived aggregate scattering distribution
Full size table

The measured extinction coefficients, their standard deviation and 95 % confidence limits (CL) (calculated from student t statistics with 2 df) are shown in Table 3 along with the absorption coefficients obtained from the scatter corrected extinction coefficients. Using the MLII-derived SVF and the absorption coefficients, E(m λ ) was calculated at the three wavelengths. The scattering correction adds an additional uncertainty that is harder to quantify. The F(m λ )/E(m λ ) values are probably no better than ±20 %, and with uncertainties in the aggregate distribution the final \(\rho_{{{\text{sa}}\lambda }}\) is no better than ±25 %. However, these errors will result in small errors in \(1 + \rho_{{{\text{sa}}\lambda }}\) since the scattering component is small. The 95 % confidence limit in the SVF (Table 1) is 8.5 %. Assuming the three sources of error to be uncorrelated, we estimate 95 % CL on the E(m λ ) values of 14, 11 and 10 % at 436, 577 and 825 nm, respectively. If we are only concerned with relative E(m λ ) values, the error limits are approximately halved since uncertainty in the SVF is not relevant since it is wavelength independent.

Table 3 Values of E(m λ ) derived from scattering corrected extinction data, the statistical uncertainty normalised to the mean value and the soot volume fraction derived from MLII
Full size table

4.5 System sensitivity

Attempts were made to measure soot in a McKenna burner at 15 mm height, an equivalence ratio of 2.1 and a laser frequency of 100 Hz. Noisy and unstable signals were observed, particularly on the 445-nm channel, and the intensity ratio gave a temperature of 1540 K. The signals were still very low and unstable when the burner was operated at an equivalence ratio of 2.34, for which a high soot concentration is expected. It is evident that the present system is unsuitable for measurements at such low soot concentrations.

Our MLII set-up, which was directly converted from a Nd/YAG pumped LII system and uses 805 nm excitation, is far from optimum for modulated LII in flames. The blackbody intensity 1700 K peaks at [27] ~1600 nm making 445 nm an unsuitable lower wavelength. In addition, diode lasers are available which can be modulated at 200 kHz and operated at 450 nm, and offers powers of up to 1 W. Given the 1/λ dependence of soot absorption, such a laser would give 10.2 times stronger excitation of the MLII signal than our present laser. With higher available laser power care would be required to ensure that the relationship between modulated LII intensity and temperature remained linear and that DC heating of the gas produced negligible temperature errors.

To measure phase delay alone, spectrally resolved radiation is not required and much more sensitive detection than we have used is available. For example, the Thor Labs Ge detector DET 50B matches the spectral response of a typical flame quite well and if we integrate the flame radiation over the response curve of that detector and compare it to a similar integral over the photomultiplier response curve of our 750-nm channel, we find the Ge detector would deliver approximately 500 times more photoelectrons, a very large increase in signal. Broadband measurements can be used to measure phase delay from which SVF, soot cooling rate and gas replacement time can derived. Such a detector, coupled with a removable interference filter to also measure a band at 900 nm, could provide a system for measuring both temperature and phase delay in flames.

5 Conclusions

We have successfully measured flame temperature in the laminar diffusion flame using MLII and assuming an E(m λ ) independent of wavelength and shown it to be consistent with CARS temperature measurements. A theory was developed that described the phase delay of the MLII signal with respect to the laser pulse. The phase delay is found to be a function of the gas replacement time in the sample volume, the soot cooling time constant and the SVF. The experimental phase delay data are fitted to the theory to provide estimates of all three quantities with small error limits. The f v measurement is based on soot heat capacity rather than soot optical properties, and we have used this independent value of f v and previously published scattering corrected extinction measurements to derive a value of E(m λ ) of 0.45 ± 0.04, 0.45 ± 0.03 and 0.42 ± 0.02 at 465, 577 and 865 nm, respectively. These values are in agreement with the values obtained by pulsed LII at 532 and 1064 nm of 0.40 [11, 17] and the review of Bond and Bergstrom that yielded a value of 0.39 at visible wavelengths [28]. Desgroux et al. [29, 30] have also shown that the ratio of E(m) at 532 and 1064 nm is essentially identical. The soot cooling rate at a soot temperature of 1714 K is shown to be consistent, but slightly lower, than that obtained by low-fluence pulsed LII soot temperature decays observed at somewhat higher soot temperatures. This new method provides a way of measuring soot cooling rates at flame temperatures to compare with those obtained at much higher temperatures in regular LII.

The limited sensitivity of the present experimental set-up is noted, and recommendations are given for increasing the sensitivity by several orders of magnitude.