Modeling laser-induced incandescence of soot: a new approach based on the use of inverse techniques

Abstract

Two LII models derived from the literature have been tested to simulate signals provided in a recently published extensive set of experimental data collected in a non-smoking laminar diffusion flame of ethylene. The first model classically accounts for particle heating by absorption and cooling by radiation, sublimation and conduction. The second one also integrates an alternative absorption term that accounts for saturation of the linear, single-photon and multi-photon absorption leading to C₂-photodesorption at high fluence, a heating flux attributable to oxidation and a cooling process based on thermionic emission. Obtained results illustrate that both models fail to reproduce the LII signals experimentally monitored on a wide range of fluences (up to ~1 J cm⁻²) regardless of the value implemented for the main parameters involved in the energy- and mass-balance equations. We therefore originally proposed a new modeling approach based on the use of inverse techniques to gain information about the specific terms that should be integrated into the calculation. The inverse procedure allows inferring the temporal evolution of the soot diameter as well as the temporal and fluence dependence of additional energy rates that have to be considered to fulfill the particle energy and mass balances while providing a complete fit with experimental data. Conclusions issued from the present work indicate that modeling soot LII using only absorption, radiation, conduction and sublimation rates (as these fluxes are generally expressed and computed in the literature) is inadequate to correctly simulate the soot heating and cooling mechanisms over a wide range of fluences. The inverse modeling procedure also gave insights concerning the relevance of integrating photolytic mechanisms such as multi-photon absorption and carbon cluster photodesorption as previously proposed by Michelsen. Additional calculations performed using a new model formulation integrating such processes finally led to predictions merging on a single curve with experimental data. Additional works should be undertaken, however, to complete this first-approach analysis especially to address the large uncertainties existing in the input parameters and equations accounting for photolytic processes that are likely to significantly impact soot LII.

1 Introduction

Soot is one of the major pollutants generated in combustion processes and one of the main contributors to anthropogenic aerosols. It results from a fuel-rich high-temperature incomplete combustion that is often encountered in practical systems. The emission of soot into the atmosphere is associated with harmful effects on human health [1] and global climate [2], such a pollutant being even fingered as a major player in global warming [3]. As a consequence, combustion-generated particles are subject to a particular attention and to increasingly stringent regulations implying the development of new technology improving the efficiency of combustion devices. A better understanding of the main pathways leading to the formation of carbonaceous nanoparticles in flames including a thorough comprehension of the specific steps insuring the transition from gaseous precursors like polycyclic aromatic hydrocarbons (PAHs) to nascent soot is necessary, however. Although major progresses have been achieved in this field during the last decades as illustrated in the detailed reviews from Richter and Howard [4], McEnally et al. [5], Wang [6] or Desgroux et al. [7], there is still an extensive need of modeling and experimental works to gain a fundamental knowledge about soot formation, growth and oxidation; optical diagnostics being especially adapted to analyze such processes in flame conditions [7].

Laser-induced incandescence has proven to be one of the most promising and powerful diagnostic technique for particle concentration and size measurements in flames and at the exhaust of combustion systems [8]. It consists in rapidly heating soot to incandescing temperature using a high-energy pulsed-laser excitation source to collect the subsequent Planck radiation emitted above the ambient flame emission. Since the early work from Melton who showed that the magnitude of the prompt LII signal could be considered as proportional to the soot volume fraction for detection wavelengths comprised in the visible spectral range [9], this technique has been used extensively for qualitative measurements of soot spatial and temporal distributions in flames [10, 11] while allowing quantitative measurements of soot volume fraction when coupled with single-pass light extinction [12, 13] or cavity ring-down spectroscopy (CRDS) [14–16]. Besides, as the decay rate of LII signals is representative of the particle cooling process, which is a function of the particle-specific surface area, time-resolved laser-induced incandescence (TIRE-LII) has been widely used to infer the diameter of soot in flame conditions [17–23]. Such an approach, however, requires the coupling of LII measurements with transmission electron microscopy analysis of sampled particles [17–19] and/or the use of theoretical LII models [18–23]. Coupled with elastic light scattering (ELS), LII can also be used to obtain information regarding the soot aggregate size [24] while data about optical properties of soot (absorption and scattering functions) can be inferred using multiple-excitation wavelength LII techniques [25–29] coupled with transmittance/extinction measurements [26–28] or by comparing measured LII signals with predicted ones using theoretical models [19, 30, 31]. In all the above-listed applications, the correct interpretation of the LII signals requires a thorough analysis of various experimental factors (including laser pulse and detection characteristics) as well as a firm understanding of the physical mechanisms and parameters (soot and gas properties among other) that control the LII process. This is why considerable efforts have been devoted during the last few years to the development of theoretical models capable of predicting the radiative emission issued from laser-heated particles over a wide range of conditions [8, 32].

LII models commonly used in the literature are derived from the one proposed by Melton [9] that is issued itself from an extensive list of works previously carried out to elucidate the details of laser-induced particle heating, cooling and size change on nanosecond to millisecond time scales (see [33] and references therein). Basically, current LII models account for particle heating by absorption and cooling by conduction to the surrounding atmosphere, emission of thermal radiation and sublimation of carbon clusters that also induces changes in the mass and size of soot. The prediction of the incandescence radiation induced by an intense pulsed-laser heating implies to solve the energy- and mass-balance equations obtained based on the governing equations describing the above-mentioned processes. Many investigations have been performed since the work of Melton in order to improve and refine LII models. Among the recent works conducted in this field, we can mention the analysis conducted by Smallwood et al. who compared different evaporation models from the literature to account for soot sublimation during the LII process focusing the attention on the significance of parameters such as the molecular weight for solid carbon associated with the heat of evaporation [34]. A modification of the Melton model was then proposed to include the effects of multiple carbon clusters subliming from the soot surface. Later, the same authors reviewed the different heat conduction models used in the LII literature and provided an overview of the physical mechanisms involved in heat conduction loss from a single spherical particle in the entire range of Knudsen number [35]. This work especially highlighted the importance of taking into account the variation of the thermal properties of the surrounding gas between the gas temperature and the particle temperature. The results of the theoretical study performed in order to evaluate the accuracy of various approximate models for heat conduction in the transition regime led the authors to recommend the Fuchs boundary-sphere model as a “default” heat conduction model in LII applications [35]. Such an approach has been followed by Bladh et al. in a modeling work aiming to analyze the impact of parameters including the gas temperature and pressure, the level of aggregation and the excitation and detection conditions on the relationship between the LII signal intensity and the soot volume fraction [36]. To do so, the LII model used by the authors (which corresponds to an updated version of the one they developed in [37]) interestingly integrates soot size and spatial energy distributions in the calculation procedure using a linear combination routine where the energy and mass balances as well as the LII responses were computed for a discrete number of initial soot diameter and laser fluence values. This extension of the current heat and mass transfer model describing the temporal LII signal complemented a previous work from Snelling et al. [38]. It, moreover, allowed reproducing satisfactorily the main features of LII signals collected using backward and right-angle configurations [39] while also contributing to a better evaluation of the influence of the spatial distribution of the laser energy on soot size inferred from TIRE-LII measurements [18]. That said, one of the most refined and advanced LII model from the literature is the one developed by Michelsen [33] who proposed a new formulation of the energy- and mass-balance equations including not only the usual terms derived from the Melton model (i.e., particle heating by absorption and cooling by sublimation, conduction and radiation) but also mechanisms accounting for oxidation, melting and annealing of the particles in addition to nonthermal photodesorption of carbon clusters from the soot surface. The inclusion of such a photodesorption mechanism was found to be particularly relevant to simulate the lack of fluence dependence of the peak LII signal commonly observed above the sublimation threshold [33]. Furthermore, integrating such a process is consistent with numerous studies, suggesting that the loss of carbon clusters induced by excitation of localized electronic states of graphite or soot at high fluences may proceed via nonthermal mechanisms such as direct photodissociation of covalent bonds within primary particles (see [40] or [41], for instance, as well as [22] and references therein). The confrontation of modeled LII fluence curve and time decays obtained using the model proposed in [33] with experimental data issued from [22] showed a good agreement, thus providing interesting insights for further developments. Then, the thorough analysis conducted in [33] regarding the physical processes involved in the heating and cooling processes of soot has been completed with a theoretical study of sub-models used to account for particle enthalpy during sublimation, conduction and oxidation [42]. Updated parameterization for average enthalpies of formation, molecular weights and total pressures of sublimed carbon clusters for use in LII models were thereby provided [42] while a temperature-dependent accommodation coefficient has also been derived from a compilation of data on the temperature dependence of translational, rotational and vibrational energy transfer for diatomic molecules colliding with graphite surfaces [43]. During the last few years, modified versions of the model developed by Michelsen in [33] have been proposed and confronted with modeling results obtained by different researcher groups from the LII community [8, 32]. One of the major conclusions emerging from such reviews and confrontation works is that current models are still not able to reproduce LII data experimentally monitored over a wide range of conditions despite the increasing number of investigations that have been undertaken to improve the predictive character of LII models. Large uncertainties still remain in the understanding of the physical processes involved in the LII phenomenon inducing a wide variability in the predictions issued from existing models.

Based on such a statement, Gouley et al. provided an extensive data set including spectrally and temporally resolved LII signals measured in an atmospheric co-flow ethylene diffusion flame stabilized on a Santoro burner [44]. Excitation wavelengths of 532 and 1,064 nm were used for fluences ranging from 0.01 to 3.5 J cm⁻²  with a temporally smooth and spatially homogeneous laser profile. Soot temperatures were inferred during the entire LII signal evolution by fitting the Planck function to obtained spectra over an interference-free wavelength range and by three-color time-resolved LII. This thorough and well-characterized experimental work provides a very interesting and useful data set for LII model development and validation.

In the present work, we propose in a first step to test the ability of two LII models derived from the literature to reproduce the signals measured by Gouley et al. [44]. The first one (called “standard model”) is issued from the work of Melton [9] and Hofeldt [45] in particular. It accounts for particle heating by absorption and cooling by radiation, sublimation and conduction. The second one (called “refined model”) is derived from the formulation proposed by Michelsen in [32, 33]. It integrates an alternative absorption term that accounts for saturation of the linear, single-photon and multi-photon absorption, a contribution from photodesorption of carbon clusters in the evaporative cooling term (the sublimation being calculated independently for each carbon cluster), a heating flux attributable to oxidation and a cooling process based on thermionic emission. The results obtained using these models will be analyzed and compared with the experimental data from Gouley et al. over a wide range of laser fluences with a 532-nm laser excitation source. The strength and weakness of both models as well as the main features of the LII process that are important to consider will be discussed. As current LII models (including those reviewed above) are mostly, if not all, issued from a direct approach where the parameters involved in the selected governing equations (such equations being a priori defined) are adjusted to obtain the best agreement between predictions and experiments, we propose in the second part of this paper to originally use inverse techniques in order to gain information about some specific terms that should be integrated in the modeling procedure so as to correctly reproduce experimental data presented in [44]. The aim of the analysis proposed here is not to define a finalized brand new model formulation (further investigations being necessary to this aim and are therefore in progress in our laboratory) but to provide insights concerning the most relevant approach to adopt in order to model soot laser-induced radiation while attempting to identify key avenues regarding the physical processes needing to be addressed and further investigated.

2 Modeling soot LII using models derived from the literature

2.1 Governing equations involved in energy and mass balances

When excited by a laser pulse, a soot particle absorbs a portion of the incident energy, which results in an increase in its internal energy and hence of its temperature. It then cools by means of different processes including sublimation that also induces changes in the mass and size of the particle. To predict the laser-induced radiation of heated soot, current models are based on a couple of differential equations with the first one accounting for the particle energy balance and the second one for its mass balance. The main differences between existing models concern the nature of the physical processes that are taken into account to establish the energy- and mass-balance equations as well as their formulations. Based on the energy rates that are considered in the present study, the energy-balance equation can be expressed as:

$$\phi_{\text{int}} = \phi_{\text{abs}} - \phi_{\text{rad}} - \phi_{\text{sub}} - \phi_{\text{cnd}} + \phi_{\text{ox}} - \phi_{\text{th}}$$

(1)

where ϕ _int represents the rate of energy stored by the particle, ϕ _abs accounts for the absorption of the laser energy, ϕ _rad describes the radiation rate by blackbody emission, ϕ _sub stands for the rate of energy loss via sublimation of carbon clusters, ϕ _cnd represents the rate of energy dissipation by conduction, ϕ _ox is the rate of energy production by oxidation and ϕ _th is the rate of energy loss by thermionic emission. The equations describing each of these physical processes will be detailed in next sections.

As the mass of a single spherical soot particle of diameter D can be written as:

$$M = \frac{\pi }{6} \cdot \rho_{\text{s}} \cdot D^{3}$$

(2)

the general equation accounting for changes in the particle mass during the LII process follows an expression of the type:

$$\frac{{{\text{d}}M}}{{{\text{d}}t}} = \frac{\pi }{2} \cdot \rho_{\text{s}} \cdot D^{2} \cdot \frac{{{\text{d}}D}}{{{\text{d}}t}} + \frac{\pi }{6} \cdot D^{3} \cdot \frac{{{\text{d}}\rho_{\text{s}} }}{{{\text{d}}T}} \cdot \frac{{{\text{d}}T}}{{{\text{d}}t}}$$

(3)

where ρ _s is the soot density.

2.1.1 Internal energy storage

The rate of change of the energy stored by a soot particle depends on its specific heat c _s, density ρ _s and volume π/6·D ³, as well as on the rate of change of the particle temperature dT/dt. According to Liu et al. [46] and Michelsen et al. [42], this rate should be expressed as follows:

$$\phi_{\text{int}} = \rho_{\text{s}} \cdot c_{\text{s}} \cdot \frac{\pi }{6} \cdot D^{3} \cdot \frac{{{\text{d}}T}}{{{\text{d}}t}}$$

(4)

To account for changes in the particle density and specific heat with temperature, the models implemented in this study incorporate formulations for these parameters proposed in [47] for graphite as done by Hadef et al. [23], Michelsen [33] or Bladh et al. [36].

2.1.2 Absorption of the laser energy

The rate of change of the energy stored by the particle is commonly equated in LII modeling using the Rayleigh–Debye–Gans theory for polydisperse fractal aggregates, which states that the emission and absorption properties of aggregates are equivalent to the emission and absorption of a comparable volume of isolated primary particles having a diameter significantly lower than the wavelength of the incident radiation. As such an assumption can be considered as valid for the type of aggregates met in the present work [44, 48, 49], the absorption cross section for each primary particle can therefore be derived using the Rayleigh approximation:

$$C_{\text{abs}} = \frac{{\pi^{2} \cdot D^{3} \cdot E\left( m \right)}}{{\lambda_{l} }}$$

(5)

where E(m) is the dimensionless refractive index function of soot.

For an incident laser beam having a temporal profile q(t), the absorption can be calculated using the following equation:

$$\phi_{\text{abs}} = C_{\text{abs}} \cdot q\left( t \right)$$

(6)

The laser intensity profile q(t) is determined based on the temporal distribution of the normalized laser power q _exp(t) weighted by the laser fluence F:

$$q\left( t \right) = \frac{{F \cdot q_{\exp } \left( t \right)}}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} q_{\exp } \left( t \right) \cdot {\text{d}}t}}$$

(7)

where t _l is the laser pulse duration.

Almost all the LII models proposed in the literature use the formulation proposed in Eq. 6 to represent the absorption rate [8]. Michelsen, however, proposed an alternative expression to distinguish between the saturation of the linear, single-photon absorption and multi-photon absorption that leads to the photodesorption of C₂ clusters at high fluence [32]:

$$\begin{aligned}\phi_{\text{abs}}& = C_{\text{abs}} \cdot \frac{{f_{1} \cdot B_{\lambda 1} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} q_{\exp } (t) \cdot dt}} \cdot \left\{ {1 - \exp \left[ { - \frac{{F \cdot q_{\exp } (t)}}{{B_{\lambda 1} }}} \right]} \right\}\\&\quad + \frac{n \cdot h \cdot c}{{\lambda_{l} }} \cdot k_{\lambda n} \end{aligned}$$

(8)

f ₁ corresponds to an empirical scaling factor for linear absorption (taken equal to 1.2 as in [32]), B _λ1 is an empirically estimated saturation coefficient for linear absorption (taken equal to 0.6 J cm⁻² [32]), h (6.62 × 10⁻³⁴ J s) is the Planck constant, c (2.998 × 10¹⁰ cm s⁻¹) is the speed of light and k _λn is the rate constant associated with the removal of C₂ clusters by photodesorption that can be expressed using the following equation:

$$k_{\lambda n} = \frac{{\lambda_{l} }}{n \cdot h \cdot c} \cdot \frac{{\sigma_{\lambda n} \cdot \pi \cdot D^{3} \cdot N_{\text{ss}} }}{6} \cdot \frac{{\left( {B_{\lambda n} } \right)^{n} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} \left[ {q_{\exp } (t)} \right]^{n} \cdot {\text{d}}t}} \cdot \left\{ {1 - \exp \left[ { - \left( {\frac{{F \cdot q_{\exp } (t)}}{{B_{\lambda n} }}} \right)^{n} } \right]} \right\}$$

(9)

where N _ss (2.8 × 10¹⁵ cm⁻²) is the density of carbon atoms on the surface of the particle, B _λn (0.5 J cm⁻²) is an empirically estimated saturation coefficient for multi-photon absorption and σ _λn (1.9 × 10⁻¹⁰ cm²ⁿ⁻¹ J¹⁻ⁿ) is an empirically determined multi-photon absorption cross section for C₂ photodesorption, considering that the number n of 532-nm photons absorbed to photodesorb C₂ is equal to 2 [32].

2.1.3 Radiation

All the LII models proposed in the literature integrate the Planck function over all wavelengths to calculate the rate of radiative emission from the particle according to:

$$\phi_{\text{rad}} = \pi \cdot D^{2} \cdot \mathop \int \limits_{0}^{\infty } \varepsilon_{\lambda } \cdot \frac{{2 \cdot \pi \cdot h \cdot c^{2} }}{{\lambda^{5} \cdot \left[ {\exp \left( {\frac{h \cdot c}{{\lambda \cdot k_{B} \cdot T}}} \right) - 1} \right]}} \cdot {\text{d}}\lambda$$

(10)

where λ is the emission wavelength, k _B (1.38 × 10⁻²³ J K⁻¹) the Boltzmann constant and ɛ _λ the emissivity that is related to the soot refractive index function following:

$$\varepsilon_{\lambda } = \frac{4 \cdot \pi \cdot D \cdot E(m)}{\lambda }$$

(11)

The wavelength dependence of the soot refractive index function has been subject to numerous studies (see [25–31] and references therein). Wavelength-independent [50] as well as wavelength-dependent [51–56] values for E(m) have been proposed in the literature depending on the spectral range considered. In the work of Gouley et al. [44], the authors used the emissivity proposed by Köylü et al. [55, 56] to infer the soot temperature from the spectrally resolved emission measurements they carried out. Referring to studies from Therssen et al. [25] and Michelsen et al. [26, 27] who used a two-excitation wavelength LII technique to estimate the E(m) ratio at 532 and 1,064 nm, Gouley et al. argued that the wavelength dependence of the soot emissivity observed by these authors was consistent with values proposed by Köylü et al. [55, 56]. On the other hand, it has been shown in [28] and [29] that the soot absorption function does not fit anymore the evolution depicted by Köylü et al. for wavelengths below 500 nm. The trends observed by Yon et al. [28] and Bejaoui et al. [29] are indeed more consistent with data from Dalzell et al. [51], Lee et al. [52] or Habib et al. [53]. This being said, as the particle temperatures that will be used as reference data in the present work have been inferred in [44] using the expression proposed by Köylü et al. for the emissivity of soot (see Eq. 12), we thus used such an equation in the theoretical models we implemented, knowing that the sensitivity of the obtained results to the expression used to account for the wavelength dependence of the E(m) function will be discussed in Sect. 2.3.2.

$$E(m) = \frac{{\lambda^{{\left( {1 - \xi } \right)}} \cdot \beta }}{6 \cdot \pi }$$

(12)

The value of the exponent ξ in Eq. 12 has been empirically determined to be equal to 0.83 with a value of 28.72 cm^−0.17 for the scaling factor β [55, 56]. Finally, the re-absorption of background emission has been taken into account in the modeling procedure by subtracting ϕ _rad(T _g ) from Eq. 10 as done by Charwath, Michelsen or Will in [32].

2.1.4 Sublimation

When the temperature of laser-heated soot reaches a value higher than ~4,000 K, the particles then sublime to produce gas-phase carbon atom clusters including C, C₂ and C₃ clusters that are the most abundant ones (see [33] and references therein). Since the early works from Eckbreth [57] and Melton [9], the evaporative cooling rate is commonly represented in LII modeling using the following equation:

$$\phi_{\text{sub}} = - \frac{{\varDelta H_{v} }}{{W_{v} }} \cdot \left( {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)_{\text{sub}}$$

(13)

Based on the work of Hofeldt [45], one can express the rate of mass loss during the sublimation process according to:

$$\left( {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)_{\text{sub}} = - \frac{{\pi \cdot D^{2} \cdot W_{v} \cdot \alpha_{M} \cdot p_{v} }}{{R_{p} \cdot T}} \cdot \sqrt {\frac{{R_{m} \cdot T}}{{2 \cdot \pi \cdot W_{v} }}} \cdot \frac{{f \cdot k_{p} \cdot T}}{{\sqrt 2 \cdot \bar{\sigma } \cdot p_{0} \cdot D \cdot \alpha_{M} + f \cdot k_{p} \cdot T}}$$

(14)

where α _M (taken equal to 0.8 as in references [32, 37, 39]) is the mass accommodation coefficient of vaporized carbon clusters, $\bar{\sigma }$ (calculated based on the values reported in [33] for C₁ to C₅ clusters) is the average molecular cross section for subliming species, k _p (1.38065 × 10⁻²² bar cm³ K⁻¹) is the Boltzmann constant in effective pressure units, R _p (83.145 bar cm³ mol⁻¹ K⁻¹) and R _m (8.314 × 10⁷ g cm² mol⁻¹ K⁻¹ s⁻²) correspond to the universal gas constant expressed in effective pressure and mass units, respectively, p ₀ (1 bar) is the ambient pressure, f (=(9γ − 5)/4) is the dimensionless Eucken correction to thermal conductivity of polyatomic gas [33] with γ = C _p /C _v corresponding to the heat capacity ratio for the gas surrounding the particles, ΔH _v is the enthalpy of formation of sublimed carbonaceous species, while W _v and p _v are the average weight and partial pressure, respectively, of sublimed carbon species. ΔH _v , W _v and p _v are temperature-dependent parameters whose values can be found in [42]. Finally, as the measurements performed by Goulay et al. have been conducted at atmospheric pressure, one can note that $\sqrt 2 \cdot \bar{\sigma } \cdot p_{0} \cdot D \cdot \alpha_{M} \ll f \cdot k_{p} \cdot T$. The last term of Eq. 14 thus becomes close to unity.

In the refined model proposed by Michelsen [32], the sublimation rate is calculated independently for each carbon cluster from C₁ to C₅. The evaporative cooling term, moreover, also includes a contribution from photodesorption of C₂ following:

$$\phi_{\text{sub}} = - \mathop \sum \limits_{j = 1}^{5} \frac{1}{{W_{j} }} \cdot \left( {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)_{{{\text{sub}},j}} \cdot \left[ {\frac{{\varDelta H_{j} \cdot \left( {P_{\text{sat}}^{{C_{j} }} - P_{\lambda n} } \right) + \varDelta H_{\lambda n} \cdot P_{\lambda n} }}{{P_{\text{sat}}^{{C_{j} }} }}} \right]$$

(15)

where W _j and ΔH _j are the molecular weight and the heat of formation of each carbon cluster species, ΔH _λn is the enthalpy required to photodesorb C₂ and P _λn is the effective pressure calculated from the rate of photodesorption of C₂ (see hereafter). The values used in the present work for ΔH _j and ΔH _λn are issued from [33, 58]. The saturation partial pressure $P_{\text{sat}}^{{C_{j} }}$ of carbon clusters C _j depends on the thermal and nonthermal vaporization rates. The contribution to the partial pressure of C _j from sublimation of the particle is generally determined by the thermal equilibrium partial pressure $P_{\text{eq}}^{{C_{j} }}$, which is controlled by the particle temperature according to the Clausius–Clapeyron equation (see Eq. 16) [9]. On the other hand, any nonthermal photodesorption of C₂ clusters will contribute to the instantaneous surface pressure of sublimed species. Thus, if the effective pressure from the nonthermal mechanism exceeds $P_{\text{eq}}^{{C_{j} }}$, thermal desorption of clusters will cease and the effective instantaneous pressure will be equal to the partial pressure of C₂ clusters issued from the direct photolytic production P _λn . On the contrary, if P _λn is small compared to $P_{\text{eq}}^{{C_{j} }}$, then the instantaneous partial pressure of C₂ at the surface of the particle will be equal to $P_{\text{eq}}^{{C_{j} }}$. To summarize, one obtains:

$$P_{\text{sat}}^{{C_{j} }} = \left\{ {\begin{array}{*{20}c} {P_{\lambda n} } & { = \frac{{k_{p} \cdot T \cdot k_{\lambda n} }}{{\pi \cdot D^{2} \cdot \alpha_{j} }} \cdot \sqrt {\frac{{2 \cdot \pi \cdot W_{j} }}{{R_{m} \cdot T}}} \quad {\text{for}}\;j = 2\;{\text{and if}}\;P_{\lambda n} > P_{\text{eq}}^{{C_{j} }} } \\ {P_{\text{eq}}^{{C_{j} }} } & { = P_{\text{ref}} \cdot \exp \left[ { - \frac{{\Delta H_{j} }}{R} \cdot \left( {\frac{1}{T} - \frac{1}{{T_{\text{ref}}^{{C_{j} }} }}} \right)} \right]\;{\text{otherwise}}} \\ \end{array} } \right.$$

(16)

where α _j is the mass accommodation coefficient of each vaporized species C _j the values of which are issued from [33], $T_{\text{ref}}^{{C_{j} }}$ are the reference temperatures (given in [32]) used in the Clausius–Clapeyron equation for each vaporized species C _j and k _λn is the rate constant associated with the removal of C₂ clusters by photodesorption (see Eq. 9).

The rate of mass loss for each carbon clusters $\left( {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)_{{{\text{sub}},j}}$ is then calculated including the convective contributions to the heat and mass transfer from the particle to the surrounding atmosphere via the B _j factor [33], which replaces the partial pressure of sublimed carbon species p _v in Eq. 14. This factor can be approximated according to [59–61] as:

$$B_{j} = \left\{ {\begin{array}{ll} {\frac{{2 \cdot {\mathcal{D}}_{\text{eff}} \cdot P_{\text{sat}}^{{C_{j} }} }}{{D \cdot \alpha_{j} \cdot \left( {\frac{{R_{m} \cdot T}}{{2 \cdot \pi \cdot W_{j} }}} \right)^{0,5} + 2 \cdot {\mathcal{D}}_{\text{eff}} }}} &\quad { {\text{if }} {\raise0.7ex\hbox{${P_{\text{sat}}^{{C_{j} }} }$} \!\mathord{\left/ {\vphantom {{P_{\text{sat}}^{{C_{j} }} } {p_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p_{0} }$}} > 3 \times 10^{ - 3} } \\ {P_{\text{sat}}^{{C_{j} }} - P_{\text{surf}}^{{C_{j} }} } &\quad { {\text{otherwise}}} \\ \end{array} } \right.$$

(17)

where $P_{\text{surf}}^{{C_{j} }}$ is the partial pressure of vaporized species C _j at the particle surface and ${\mathcal{D}}_{\text{eff}}$ is the total effective diffusion coefficient whose calculation procedure is detailed in [33].

2.1.5 Heat conduction

The formulation of the equation used in LII modeling to account for the energy loss at the particle surface due to collisions with the surrounding gas molecules depends on the heat conduction regime. This one is basically defined using the dimensionless Knudsen number Kn that corresponds to the ratio between the mean free path of gas molecules λ _g and the characteristic length of the soot particles L _c typically chosen as being their diameter or radius [35]. At atmospheric pressure and for a flame temperature of the order of 1,700 K as it is the case in the work of Gouley et al. [44], the conductive cooling rate can be calculated assuming a free molecular flow regime as the particle size is greatly inferior to the mean free path estimated using the formulation proposed by Bird for an equilibrium hard sphere gas (see [35]):

$$\lambda_{g} = \frac{1}{{\sqrt 2 \cdot \sigma \cdot n_{g} }}$$

(18)

where the number density of gas molecules n _g is related to the ambient pressure p ₀, the temperature of the surrounding gases T _g and the Boltzmann constant k _p by p ₀ = n _g ·k _p ·T _g .

Based on the conduction model proposed by McCoy and Cha [62] used in references [9, 38, 45], for instance, one obtains the flowing expression of the heat conduction rate:

$$\phi_{\text{cnd}} = \frac{{2 \cdot \kappa_{a} \cdot \pi \cdot D^{2} }}{{D + G \cdot \lambda_{g} }} \cdot \left( {T - T_{g} } \right)$$

(19)

where κ _a is the thermal conductivity of the surrounding gases and G is a heat transfer factor that can be expressed according to [62] as:

$$G = \frac{8 \cdot f}{{\alpha_{T} \cdot (\gamma + 1)}}$$

(20)

α _T being the thermal accommodation coefficient determining the probability of a molecule to undergo energy exchange with a soot particle during a collision.

As G·λ _g  ≫ D in the free molecular flow regime, the denominator of Eq. 19 can thus be simplified by suppressing D. Then, λ _g can be replaced in Eq. 19 by its expression given in Eq. 18, while the thermal conductivity κ _a can be replaced by Eq. 21 according to [32].

$$\kappa_{a} = \frac{f \cdot R}{{\left( {\gamma - 1} \right) \cdot \sigma \cdot N_{A} }} \cdot \sqrt {\frac{{R_{m} \cdot T_{g} }}{{\pi \cdot W_{a} }}}$$

(21)

N _A (6.02214 × 10²³ mol⁻¹) being the Avogadro constant.

One finally obtains the following expression of the energy loss by conduction:

$$\phi_{\text{cnd}} = \frac{{\pi \cdot D^{2} \cdot \alpha_{T} \cdot p_{0} }}{{R_{p} \cdot T_{g} }} \cdot \sqrt {\frac{{R_{m} \cdot T_{g} }}{{2 \cdot \pi \cdot W_{a} }}} \cdot \left( {C_{p} - \frac{R}{2}} \right) \cdot \left( {T - T_{g} } \right)$$

(22)

where W _a (28,74 g mol⁻¹) is the average molecular weight of air used as a surrogate for flame gases, C _p is its molar heat capacity at constant pressure based on the data issued from [63] and R (8.3145 J mol⁻¹ K⁻¹) is the universal gas constant.

The crucial parameter in the conduction term is the thermal accommodation coefficient whose values have been subject to numerous investigations [30, 43, 64]. In the present work, α _T has been set to 0.3 as in [23, 33, 36, 39] while a sensibility analysis of modeled LII signals to this parameter will be proposed in Sect. 2.3.2.

2.1.6 Oxidation

The oxidation of soot by the oxygen available in the surrounding atmosphere is an exothermic process that induces changes in the particle temperature and diameter. Assuming that the C + O₂ reaction only generates CO and that this specie partially accommodates with the surface prior to desorption [33], the enhancement in the particle energy by oxidation can be estimated according to Michelsen by:

$$\phi_{\text{ox}} = - \frac{{\left( { - \Delta H_{ox} - 2 \cdot \alpha_{T} \cdot C_{p}^{CO} \cdot T} \right)}}{{2 \cdot W_{1} }} \cdot \left( {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)_{\text{ox}}$$

(23)

where ΔH _ox is the enthalpy of the oxidation reaction, C ^CO _p is the temperature-dependent molar heat capacity of CO whose values are issued from [63] and W ₁ is the molecular weight of atomic carbon.

Finally, the rate loss caused by oxidation can be written as follows:

$$\left( {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)_{\text{ox}} = - \frac{{2 \cdot \pi \cdot D^{2} \cdot W_{1} \cdot k_{\text{ox}} }}{{N_{A} }}$$

(24)

where k _ox is the overall rate constant for oxidation that can be calculated following the procedure proposed in [33] incorporating a parameterization provided by Strickland-Constable et al. [65, 66] and modified by Hiers [67] for soot oxidation.

2.1.7 Thermionic emission

In the model proposed by Michelsen in [8, 32], an additional cooling process by thermionic emission has been added to the energy-balance equation. This term accounts for energy loss due to the thermal ejection of electrons from the particle. It can be estimated based on the Richardson–Dushman approximation [68] that involves a work function ϕ (7.37 × 10⁻¹⁹ J) and the mass of an electron m _e (9.1095 × 10⁻³⁵ J s² cm⁻²) following:

$$\phi_{\text{th}} = \frac{{4 \cdot \phi \cdot m_{\text{e}} \cdot \left( {\pi \cdot D \cdot k_{\text{B}} \cdot T} \right)^{2} }}{{h^{3} }} \cdot \exp \left( { - \frac{\phi }{{k_{\text{B}} \cdot T}}} \right)$$

(25)

2.2 Definition of the tested models and presentation of the resolution method

The main differences between the two models that have been implemented in this work (i.e., the so-called standard and refined models) concern the nature of the physical processes considered to establish the energy- and mass-balance equations as well as their formulation. Absorption, conduction, radiation and sublimation have been integrated in the standard model while additional contributions from oxidation and thermionic emission have been introduced into the refined model in addition to the use of different formulations for the absorption and sublimation rates (see Table 1). The time dependence of the temperature and diameter of the particle has then been calculated by solving the coupled differential equations for temperature and mass. The obtained system can be treated as a problem of minimization of two functions f(T, D) and g(T, D) whose unknowns are T and D according to:

$$\left\{ {\begin{array}{*{20}c} {f\left( {T,D} \right) = } & {\phi_{\text{int}} - \left( {\phi_{\text{abs}} - \phi_{\text{rad}} - \phi_{\text{sub}} - \phi_{\text{cnd}} + \phi_{\text{ox}} - \phi_{\text{th}} } \right)} & { = 0 } \\ {g\left( {T,D} \right) = } & {\frac{{{\text{d}}M}}{{{\text{d}}t}} - \frac{\pi }{2} \cdot \rho_{\text{s}} \cdot D^{2} \cdot \frac{{{\text{d}}D}}{{{\text{d}}t}} - \frac{\pi }{6} \cdot D^{3} \cdot \frac{{{\text{d}}\rho_{\text{s}} }}{{{\text{d}}T}} \cdot \frac{{{\text{d}}T}}{{{\text{d}}t}}} & { = 0} \\ \end{array} } \right.$$

(26)

First-order Euler method as well as second-order and fourth-order Runge–Kutta methods is commonly used to solve such coupled differential equations [32]. In the case of stiff problems like those met at high fluence, the above-mentioned solving methods may induce stability problems, however, depending on considered conditions [69]. This would especially explain why Bladh, for example, used an explicit solver based on a combination of fourth- and fifth-order Runge–Kutta calculations while passing to a variable-order solver based on numerical differentiation formulas at high fluence [70]. To avoid any calculation stability issues, a Newton iterative method [71] has been implemented here to solve the present nonlinear problem, the temporal discretization of the mass- and energy-balance equations being achieved following the Crank–Nicolson scheme as done in our previous modeling works [72–74]. Since Gouley et al. used a spatially homogeneous laser profile to perform their experiments, no spatial discretization was therefore needed. That said, the Newton’s algorithm applied to the LII modeling procedure can be expressed as follows:

$$\left\{ {\begin{array}{*{20}c} {{\text{derv}} = \frac{{\partial f\left( {T_{\kappa } ,D_{\kappa } } \right)}}{\partial T} \cdot \frac{{\partial g\left( {T_{\kappa } ,D_{\kappa } } \right)}}{\partial D} - \frac{{\partial f\left( {T_{\kappa } ,D_{\kappa } } \right)}}{\partial D} \cdot \frac{{\partial g\left( {T_{\kappa } ,D_{\kappa } } \right)}}{\partial T}} \\ {T_{\kappa + 1} = T_{\kappa } - \frac{{f\left( {T_{\kappa } ,D_{\kappa } } \right) \cdot \frac{{\partial g\left( {T_{\kappa } ,D_{\kappa } } \right)}}{\partial D} - g\left( {T_{\kappa } ,D_{\kappa } } \right) \cdot \frac{{\partial f\left( {T_{\kappa } ,D_{\kappa } } \right)}}{\partial D}}}{\text{derv}}} \\ {D_{\kappa + 1} = D_{\kappa } - \frac{{g\left( {T_{\kappa } ,D_{\kappa } } \right) \cdot \frac{{\partial f\left( {T_{\kappa } ,D_{\kappa } } \right)}}{\partial T} - f\left( {T_{\kappa } ,D_{\kappa } } \right) \cdot \frac{{\partial g\left( {T_{\kappa } ,D_{\kappa } } \right)}}{\partial T}}}{\text{derv}}} \\ \end{array} } \right.$$

(27)

where κ is the iteration index. The number of iteration has been fixed according to a stopping criterion, implying that the values of the residuals related to mass and energy balances (Eq. 26) are lower than 10⁻³⁰ and 10⁻¹⁰, respectively.

Table 1 Summary of equations used in the two LII models implemented in this work

Knowing the temporal evolution of the particle temperature and diameter, the LII signal can then be calculated using the Planck function integrated over the detection spectral range Δλ _det while taking into account the evolution of the E(m) function as a function of the wavelength as explained in Sect. 2.1.3:

$${\text{SLII}} = 8 \cdot \pi^{3} \cdot D^{3} \cdot h \cdot c^{2} \cdot \left\{ {\mathop \int \limits_{{\varDelta \lambda_{\det } }}^{{}} \frac{E(m)}{{\lambda^{6} }} \cdot \left( {\frac{{{\mathcal{R}}_{\lambda \det } \cdot d\lambda }}{{\left[ {\exp \left( {\frac{h \cdot c}{{\lambda \cdot K_{\text{B}} \cdot T}}} \right) - 1} \right]}} - \frac{{{\mathcal{R}}_{\lambda \det } \cdot d\lambda }}{{\left[ {\exp \left( {\frac{h \cdot c}{{\lambda \cdot K_{\text{B}} \cdot T_{g} }}} \right) - 1} \right]}}} \right)} \right\}$$

(28)

${\mathcal{R}}_{\lambda \det }$ being the spectral characteristics of the detection system.

2.3 Results and discussion

2.3.1 Comparison of experimental and predicted LII signals

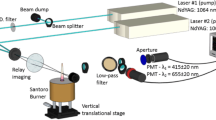
In the work from Gouley et al., soot particles generated in a non-smoking laminar diffusion flame of ethylene stabilized on a Santoro burner were irradiated with the 1,064- or 532-nm output from an injection-seeded Nd:YAG laser providing pulses with a smooth temporal profile. Spatially homogeneous beams were obtained using an optical system described in [44]. Interference-free LII temporal profiles were recorded using a gated PMT module with a bandpass filter centered at 681.8 nm (see [44] for more information concerning the experimental setup and methodology). The calculations performed in the present work have been conducted integrating the spectral characteristics of the detection system used by Gouley et al. while considering a 532-nm laser excitation wavelength, an ambient pressure of 1 bar, a temperature of the surrounding gases of 1,676 K and a primary particle size of ~33 nm for laser fluences ranging from 0.01 to 1 J cm⁻². The equation and parameters used in the modeling procedure have been described in Sect. 2.1 and 2.2. The soot absorption function values are issued from the emissivity proposed by Köylü et al. [55, 56] (leading to a E(m) value of 0.286 at 532 nm), the thermal accommodation coefficient α _T has been set to 0.3 as did in [23, 33, 36, 39] and the physical properties of soot (like their density or specific heat) as well as the physical properties of sublimed species or flame gases have been considered as temperature dependent (see Sect. 2.1).

Experimental and modeled LII fluence curves are plotted in Fig. 1a together with the evolution of the peak soot temperature as a function of the laser fluence (Fig. 1b). The curves presented in Fig. 1a have been normalized to 1 for a fluence of 0.174 J cm⁻² above which measurements show a lack of fluence dependence of the peak LII signal. Based on these curves, one can first note that the standard model underestimates the peak LII signal in the low and intermediate fluence regime (<0.2 J cm⁻²) while overpredicting it at higher fluences. Such a trend is consistent with the predicted peak soot temperatures (see Fig. 1b) that are inferior to the measured ones until ~0.174 J cm⁻² while they significantly exceed experimental data and even the sublimation temperature of C₂ (4,456.59 K [44]) for higher fluences. While the refined model also underestimates the normalized peak LII signal for fluences below 0.2 J cm⁻² (such a point will be discussed in Sect. 2.3.2 with respect to the low E(m) value selected here), it is worthy to note that this model reproduces well the plateau region of the fluence curve [8] where the LII response becomes nearly independent of the fluence. This difference in behavior compared with the standard model is attributable to the inclusion of the multi-photon absorption term that leads to the nonthermal photodesorption of C₂ clusters at high fluence (see Sect. 2.1.2). On the other hand, although the agreement between measured and modeled peak LII signals is better above 0.2 J cm⁻² when using the refined model, the predicted peak soot temperatures largely exceed experimental ones for such fluences. The overestimation is even more important in this case than with the standard model.

Fig. 1

Fluence dependence of the peak LII signal (a) and evolution of the maximal soot temperature as a function of the laser fluence (b)—Comparison of experimental results with simulated data issued from the use of the standard and refined models. Fluence curves on a have been plotted as a function of the laser fluence using the maximum of LII signal temporal profiles normalized to 1 at 0.174 J cm⁻²

To analyze the obtained results further in detail, we also compared the measured and modeled LII time decays in Fig. 2a, and we plotted in Fig. 2b and c the predicted evolution of the soot temperature and diameter for fluences ranging from 0.030 to 0.997 J cm⁻². The maximum values of the time-resolved LII signals have been scaled in Fig. 2a to facilitate the comparison of the shapes of the temporal profiles. One can thus note that both the measured and the modeled LII time decays exhibit a common shape with a steep rise of the LII intensity during the heating of the particle and a slower decay during the cooling phase. At low fluence (below ~0.07 J cm⁻²), the adequacy between simulated and experimental data is globally good although both models tend to slightly underpredict the LII decay rate. For such a fluence range, the temperature of the particle increases during the laser pulse without reaching the sublimation temperature (see Fig. 2b). In parallel, the diameter is predicted to slightly rise (see Fig. 2c). Such a behavior results from a decrease in the particle density with increasing temperature due to the temperature dependence of the physical parameters used in the modeling procedure. For fluences higher than 0.08 J cm⁻² on the other hand, one can first observe a temporal shift in the steep rise of modeled LII signals that can be attributed to an underpredicted energy absorption rate (see comments concerning the soot absorption function) while the decay times of LII signals which become very fast with increasing fluences are not satisfactorily predicted anymore. The standard model tends to underpredict the LII decay rate as observed in Fig. 2a for fluences of 0.272 or 0.997 J cm⁻² while the refined model globally overpredicts it (see, for instance, the signals predicted for fluences of 0.174 or 0.997 J cm⁻²). Figure 2b, moreover, illustrates the fact that particles quickly reach and surpass the maximal temperature measured by Gouley et al. (represented by a black line) at high fluence. Particles thus become superheated and then cool especially by sublimation, which causes a decrease in the soot diameter as depicted in Fig. 2c. The initial slight increase in the particle size attributable to the temperature dependence of soot density is still simulated with the standard model while such an effect is overwhelmed when using the refined model due to a more rapid particle mass loss [33]. This being said, modeled temperatures always reach higher values when using the refined model instead of the standard one, which can be related to a higher absorption behavior. The decrease in the particle size is, moreover, much more important in this case reflecting faster and more important evaporative heat and mass loss.

Fig. 2

Evolution of LII signal (a), soot temperature (b) and soot diameter (c) as a function of time for laser fluences ranging from 0.030 to 0.997 J cm⁻². Modeled LII time decays are plotted together with measured ones on (a)

Such observations are perfectly confirmed by Fig. 3 that depicts the temporal evolution of absorption (a) and sublimation (b) rates for both models as well as the evolution of the saturation partial pressure of sublimed species (c) for different fluences comprised between 0.030 and 0.997 J cm⁻². The absorption rate thus appears to be much larger using the refined model because of the inclusion of the multi-photon absorption. To highlight such a point, we separated in Fig. 3a the contribution of the different absorption mechanisms involved in the refined model. As one can see, if the absorption term for multi-photon photodesorption does not play a major part at low fluence, the contribution of such a mechanism to the global absorption rate becomes predominant at high fluence (although the difference between the absorption rates predicted using the standard and the refined models is more pronounced at fluences ~0.2 J cm⁻²). Besides, the multi-photon absorption that enhances the absorption rate does not contribute significantly to the particle heating as explained in [32]. Therefore, most of the energy from the additional absorbed photons leads to the photodesorption of C₂ clusters, which directly affects the particle mass loss according to Eq. 15. As a result, higher sublimation rates are estimated based on the refined model as observed in Fig. 3b. The nonthermal photodesorption of carbon clusters also leads to a sharper decay in the LII signal after the peak value at high fluence as previously observed in Fig. 2. It also reduces the magnitude of the LII response at intermediate and high fluences, thus contributing to obtain the plateau region above 0.2 J cm⁻² (see Fig. 1a). The higher sublimation rate observed with the refined model is finally well correlated with the evolution of the partial pressure of sublimed species plotted in Fig. 3c (p _v being determined according to $p_{v} = \mathop \sum \limits_{j} P_{\text{sat}}^{{C_{j} }}$ [42]).

Fig. 3

Comparison of the time dependence of absorptive heating rate (a), evaporative cooling rate (b) and partial pressure of sublimed carbon species (c) issued from the standard and refined models for laser fluences ranging from 0.030 to 0.997 J cm⁻²

To better illustrate the main differences in the energy rates calculated using the two considered models, Fig. 4 reports the temporal evolution of each of the energy production and loss terms involved in the energy-balance equation (Eq. 1) for fluences ranging from 0.030 to 0.997 J cm⁻². First of all, we can note that the temporal profiles of the different energy fluxes are in good agreement with those reported in previous theoretical works based on the use of similar models [32, 33]. At low fluence (when the temperature of soot is well below the sublimation threshold), the LII decay rates appear to be predominantly controlled by conductive cooling for both models. One can, however, note the presence of an initial higher sublimation rate in the refined model that is related to the photodesorption of C₂ as explained above. Following explanations given in [32], this process is responsible for the specific evolution of the particle diameter during the laser pulse at low fluence (see Fig. 2c) with a smaller peak diameter that would be anticipated solely from the decrease in the density with the temperature. In these conditions, the thermionic cooling process and the heating by oxidation have only little effects on the LII signals. At higher fluences (>0.1 J cm⁻²), sublimation becomes the most important process involved in the particle cooling for the standard model, while both the evaporative cooling (including the contribution of nonthermal photodesorption) and the thermionic emission play an important part in the energy balance of the refined model. The oxidation rate continues to have a negligible effect on the simulated signals, however.

Fig. 4

Temporal evolution of energy heating and cooling rates predicted using the standard (a) and refined (b) models for fluences of 0.030, 0.174 and 0.997 J cm⁻²

2.3.2 Sensitivity of predicted LII signals to E(m, λ) and α _T

As discussed in Sect. 2.1.3, the choice of the model accounting for the wavelength dependence of the soot refractive index function is of importance for both the absorption and radiation rates. Furthermore, we noted in the previous section that the two tested models underestimate the peak LII signal in the low and intermediate fluence regime (<0.2 J cm⁻²), which can be related to factors including a lack of energy absorption. We thus performed additional simulations integrating the wavelength dependence of the E(m) function proposed by Yon et al. [28], Dalzell et al. [51], Habib et al. [53] in addition to the previous calculations carried out with the expression proposed by Köylü et al. [55, 56]. Corresponding fluence curves are plotted in Fig. 5a together with the peak soot temperature profiles (see Fig. 5b) for the standard and the refined models. The obtained results show that the standard model fails to reproduce the experimentally monitored fluence curve on the entire range of fluences regardless of the selected E(m, 532) value. More consistent results can be obtained with the refined model on the other hand. Between all the values proposed in the literature and tested here for the absorption function, the one issued from the work of Yon et al. gives the best agreement between simulated and experimental data although E(m, 532) values of the order of 0.487 and 0.526 should be selected in order to fit the peak LII responses for fluences up to around 0.2 J cm⁻² with the refined and the standard models, respectively. As the calculated peak temperature increases with the E(m) value, the temperature overprediction previously pointed out therefore significantly increases too. Consequently, even by adjusting the value of the soot absorption function, no fit between experimental and modeled results can be achieved.

Fig. 5

Sensitivity of the standard and refined models to the wavelength-dependent soot refractive index function. Experimental and simulated fluence curves are compared on (a) while corresponding peak soot temperature profiles are plotted on (b)

As far as LII time decays are concerned, Fig. 6 reports signals obtained for both models with different values of the thermal accommodation coefficient α _T using soot absorption functions proposed by Yon et al. (Figure 6a), Dalzell et al. (Figure 6b) and Köylü et al. (Figure 6c). Results issued from the use of the optical properties proposed by Habib et al. [53] have not been reported on this figure as they lead to the largest gap between modeled and experimental data as already illustrated in Fig. 5. In addition to the value of 0.3 previously selected, we also fixed α _T as being equal to 0.23 according to Dreier and Kock [32] and 0.37 according to Liu [30] while the temperature-dependent accommodation coefficient proposed by Michelsen et al. in [43] has also been implemented. One can first note that the E(m, 532) values proposed by Dalzell et al. and Köylü et al. are more suitable to reproduce the data from Gouley et al. at 0.174 J cm⁻² with the standard model. The agreement is not satisfactorily for other fluences on the other hand. Considering the refined model, experimental and modeled LII time decays merge on a single curve at low fluence (0.080 J cm⁻²) when using the E(m, 532) value proposed by Yon et al. Results still diverge, however, at higher fluences despite the relatively good agreement observed on the basis of the fluence curves (see Fig. 5a). This can be explained by the overpredicted soot temperature (see Fig. 5b) inducing a too important particle mass loss as explained in Sect. 2.3.1. The implementation of the different models accounting for the wavelength dependence of E(m) in the radiation term has no significant impact on the obtained LII responses. Such a result is consistent with the fact that radiation is not of major importance in the energy balance (see Fig. 4) especially for the time range considered here. By the same way, modifications of the thermal accommodation coefficient only have a minor effect on the simulated LII time decays. If such a trend is quite expected at high fluence (sublimation and thermionic emission being the most important processes involved in the particle cooling as illustrated in Fig. 4), it is noteworthy that the adjustment of α _T (in the limit of the values commonly used in the literature) cannot improve the agreement between modeled and measured data, even at low fluence (such a conclusion being coherent with the role played by conduction in the cooling process that really becomes important at higher decay times).

Fig. 6

Sensitivity of the standard and refined models to wavelength-dependent soot refractive index function and thermal accommodation coefficient. Experimental LII time decays are compared with predicted ones using soot absorption functions proposed by Yon et al. (a), Dalzell et al. (b) and Köylü et al. (c) for different values of the thermal accommodation coefficient (reported in the chart legend) and fluences ranging from 0.080 to 0.997 J cm⁻²

All the results presented in this section clearly illustrate that the two theoretical models implemented in this work are not able to predict the data from Gouley et al. on a wide range of fluences regardless of the main parameters used in the modeling procedure. We actually also performed a complete sensitivity analysis to better apprehend the impact of parameters such as σ _λn , B _λn , or ΔH _λn on the LII response using a model similar to the refined one without being able to predict experimentally monitored signals measured in an atmospheric jet flame with fluences ranging up to 0.7 J cm⁻² [73]. The inclusion of a multi-photon absorption process leading to the photodesorption of C₂ clusters as proposed by Michelsen seems of interest especially to better reproduce the lack of fluence dependence of the peak LII signal above the sublimation threshold. Nevertheless, the formulation as well as the empirical parameterization of the equations accounting for such processes (as they have been implemented in the present study) appears to be not satisfactorily to reproduce experimental LII signals from [44] prompting demand for additional studies to be conducted. This is the reason why we proposed in the present work a new approach (detailed in next section) to model LII signals using inverse techniques.

3 Modeling soot LII using inverse techniques

The new approach proposed to gain information about the specific terms that should be integrated in the LII modeling is based on the use of inverse techniques [75]. The procedure (schematically summarized in Fig. 7) consists in using a baseline model (called direct model) to solve the energy-balance equation, considering that the evolution of the diameter of soot particles during the LII process is known as a first stage. A hypothetical soot diameter history is thus used as input data to solve the energy-balance equation. The evolution of the particle temperature can then be calculated and integrated into the Planck function to simulate a LII signal. In a second stage, the evolution of the soot diameter is considered as unknown and the aim of the inverse approach is to estimate the value that must take this parameter (i.e., D) to minimize the difference between the experimentally monitored signal and the LII response simulated using the direct model. When an optimal solution fulfilling such a condition is determined, the analysis of the obtained results allows inferring the temporal evolution of additional energy rates that have to be taken into account to verify the particle energy- and mass-balance equations while providing a perfect fit with experimental data. Additional analyses performed using modified direct models integrating the newly determined energy rates can also be operated afterward with a view to obtain information regarding the parameterization of the equations accounting for the different processes involved in soot LII.

Fig. 7

Schematic representation of the modeling procedure adopted in this work using inverse techniques

3.1 Mathematical formulation of the problem

3.1.1 Direct problem

Assuming that the temporal evolution of the particle diameter is known, only the energy-balance equation needs to be solved to simulate a LII signal (using Eq. 28) for a given fluence. This implies to define the different base terms to be implemented in the direct model. In the present case, we integrated the absorption, radiation, conduction and sublimation rates without taking into account the oxidation term (see Sect. 2.1.6), which has only a negligible effect on the calculated signals (as illustrated in Sect. 2.3.1) and the rate of energy loss by thermionic emission that was initially not introduced in the model proposed by Michelsen [33]. In these conditions, the direct problem can be expressed as follows:

$$\phi_{\text{abs}} - \phi_{\text{rad}} - \phi_{\text{cnd}} - \underbrace {{\left( { - \frac{{\varDelta H_{v} }}{{W_{v} }} \cdot \frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)}}_{\text{Sublimation}} = \underbrace {{M \cdot c_{s} \cdot \frac{{{\text{d}}T}}{{{\text{d}}t}}}}_{\text{Internal energy}}$$

(29)

Unlike the two models tested in Sect. 2.3, the use of a hypothetical soot diameter history as input data allows addressing the problem without needing to define a priori a formulation of the mass loss expression involved in the sublimation rate. It thus brings more degree of freedom in the formulation that will be subsequently attributed to the equation accounting for such a process (calculation carried out independently for each carbon cluster or not, inclusion of an additional contribution related to the photodesorption of C₂ clusters or not, etc.).

3.1.2 Inverse problem

The objective of the inverse procedure is to determine the evolution of the particle diameter (considered as unknown now) to obtain the best agreement between experimental data and LII signals predicted using the direct model. The inverse problem can be formulated as an optimization procedure which consists in minimizing an objective or cost function ${\mathcal{J}}\left( D \right)$ defined as:

$${\mathcal{J}}\left( D \right) = \frac{1}{2} \cdot \mathop \int \limits_{t = 0}^{{t_{f} }} \left\| {{\text{SLII}}\left( {t,D} \right) - {\text{SLII}}^{ * } \left( t \right) } \right\|^{2} \cdot {\text{d}}t$$

(30)

where SLII* is the measured LII signal for a given time t, SLII is the calculated LII signal issued from the direct model and t _f is the final measurement time. Such an optimization problem being considered as nonlinear, the minimization of the cost function can be carried out using direct search methods or descent methods [76–80]. Direct search techniques only require the objective function values while descent methods (also called gradient-based methods) imply not only the ${\mathcal{J}}\left( D \right)$ function evaluations but also its first and possibly higher-order derivatives. Among the gradient-based class of unconstrained optimization techniques, the quasi-Newton or variable metric methods (VMM) [81–83] are of interest as they are very stable and have good theoretical and practical convergence properties [84]. Such methods for unconstrained minimization are iterative. Starting with an initial guess D _k=0, they generate a sequence D _κ defined by:

$$D_{\kappa + 1} = D_{\kappa } + \eta_{\kappa } \cdot d_{\kappa }$$

(31)

where η _κ is the search step size in going from iteration κ to iteration κ + 1 and d _κ is the direction of descent [79]. One should note that η _κ corresponds to a scalar while the diameter D and the direction of descent d are vectors composed of N _t components resulting from the temporal discretization (i.e., $D_{k} = \left[ {D_{1} , D_{2} , \ldots ,D_{i} , \ldots , D_{{N_{t} }} } \right]^{T}$ where the superscript T denotes the matrix transpose symbol). The direction vector can be related to the Hessian matrix $\nabla^{2} {\mathcal{J}}_{\kappa }$ and to the gradient ${\nabla \mathcal{J}}_{\kappa }$ of the objective function according to:

$$d_{\kappa } = - \left[ {\nabla^{2} {\mathcal{J}}_{\kappa } } \right]^{ - 1} \cdot \nabla {\mathcal{J}}_{\kappa }$$

(32)

In variable metric methods, the Hessian matrix ${\nabla }^{2} {\mathcal{J}}_{\kappa }$ is replaced by its positive-definite approximation H _κ corresponding to a N _t  × N _t matrix.

$$d_{\kappa } = - H_{\kappa }^{ - 1} \cdot \nabla {\mathcal{J}}_{\kappa }$$

(33)

Each H _κ matrix is constructed iteratively so that H _κ=0 is an arbitrary positive-definite matrix (usually taken as the identity matrix) and H _κ+1 is determined from H _κ in such a way that it is positive definite, close as possible to H _κ while satisfying the quasi-Newton condition:

$$H_{\kappa + 1} \cdot {\mathcal{S}}_{\kappa } = {\mathcal{Y}}_{\kappa }$$

(34)

where

$${\mathcal{S}}_{\kappa } = D_{\kappa + 1} - D_{\kappa }$$

(35)

and

$${\mathcal{Y}}_{\kappa } = {\nabla \mathcal{J}}_{\kappa + 1} - {\nabla \mathcal{J}}_{\kappa }$$

(36)

H _κ+1 being calculated using the BFGS (Broyden–Fletcher–Goldfarb–Shanno) formula [78, 82, 85]:

$$H_{\kappa + 1} = H_{\kappa } + \frac{{{\mathcal{Y}}_{\kappa } \cdot \left[ {{\mathcal{Y}}_{\kappa } } \right]^{T} }}{{\left[ {{\mathcal{Y}}_{\kappa } } \right]^{T} \cdot {\mathcal{S}}_{\kappa } }} - \frac{{\left( {H_{\kappa } \cdot {\mathcal{S}}_{\kappa } } \right) \cdot \left[ {\left( {H_{\kappa } \cdot {\mathcal{S}}_{\kappa } } \right)} \right]^{T} }}{{\left[ {{\mathcal{S}}_{\kappa } } \right]^{T} \cdot H_{\kappa } \cdot {\mathcal{S}}_{\kappa } }}$$

(37)

The gradient of the cost function used in the expression of the direction vector (see Eq. 33) can be determined based on a sensitivity problem that can be expressed in the present case as follows:

$$\nabla {\mathcal{J}} = \left[ { \ldots ,\mathop \int \limits_{t = 0}^{{t_{f} }} {\mathcal{X}}\left( {t,D_{i} } \right) \cdot \left[ {{\text{SLII}}\left( {t,D} \right) - {\text{SLII}}^{ * } \left( t \right)} \right] \cdot {\text{d}}t, \ldots } \right]^{T}$$

(38)

${\mathcal{X}}$ being the sensitivity coefficient vector which expresses the sensitivity of the LII response ∆SLII to a slight perturbation of the particle diameter ∆D. It is defined as the first derivative of the LII signal with respect to the particle diameter D:

$${\mathcal{X}}\left( {t,D_{i} } \right) = \frac{{\partial {\text{SLII}}\left( {t,D} \right)}}{{\partial D_{i} }}$$

(39)

In the present work, the sensitivity problem has been solved using an approximation by finite differences of Eq. 39 assuming small ∆D such as [76]:

$${\mathcal{X}}\left( {t,D_{j} } \right) = \frac{{{\text{SLII}}\left( {t,\left[ {D_{1} , \ldots , D_{i} + \epsilon \cdot D_{i} , \ldots , D_{{N_{t} }} } \right]} \right) - {\text{SLII}}\left( {t,\left[ {D_{1} , \ldots , D_{i} , \ldots , D_{{N_{t} }} } \right]} \right)}}{{\epsilon \cdot D_{i} }}$$

(40)

where ϵ is a small real number (10⁻⁶), the direct model being solved N _t times at each iteration to calculate the sensitivity coefficient.

Finally, the determination of the optimal step size η _κ has been carried out using an inexact line search method based on the Armijo rule [78], which is one of the several inexact line search procedures guaranteeing a sufficient degree of accuracy to ensure the algorithm convergence. It involves starting with a relatively large estimate of the step size for movement along the search direction and iteratively shrinking the step size until a decrease in the objective function satisfies the following Armijo condition:

$${\mathcal{J}}_{\kappa } \left( {D_{\kappa } + \eta_{\kappa } \cdot d_{\kappa } } \right) \le {\mathcal{J}}_{\kappa } \left( {D_{\kappa } } \right) + \omega \cdot \eta_{\kappa } \cdot \left[ {\nabla {\mathcal{J}}_{\kappa } } \right]^{T} \cdot d_{\kappa }$$

(41)

where ω is a real number (0 < ω < 1).

The iterative procedure used for the implementation of the variable metric method based on the BFGS formulation is summarized in the algorithm of Appendix 1. The total measurement time (49.5 ns) has been divided into 495 time steps (i.e., dt = 100 ps) for the numerical calculations. As far as the stopping criterion is concerned, such an issue is commonly addressed according to the value of the objective function in the absence of measurement errors (the iterative process ceasing when the objective function reaches a value considered as sufficiently small depending on the characteristics of the considered problem). In the more realistic case where data contain some measurement errors, the discrepancy principle [86, 87] should be used to establish the stopping criterion and ensure the stability of the solution. In this case, the iterations are stopped when the residuals between measured and estimated LII signals are of the same order of magnitude as the measurement errors, i.e.,:

$${\text{SLII}}\left( {t,D} \right) - {\text{SLII}}^{ * } \left( t \right) \approx \sigma_{\text{err}}$$

(42)

where σ _err is the standard deviation of the measurement errors. Substituting this approximation into Eq. 30 leads to the following expression of the stopping criterion:

$${\mathcal{J}}\left( D \right) < \frac{1}{2} \cdot \sigma_{\text{err}}^{2} \cdot t_{f}$$

(43)

corresponding to ${\mathcal{J}}\left( D \right) < 2.5 \times 10^{ - 14}$ for a standard deviation of 10⁻³.

3.2 Results and discussion

3.2.1 Results obtained using the equations from the standard model in the formulation of the direct problem

Starting with no specific assumptions concerning the nature of the physical processes that should be included in the modeling procedure, the direct problem has been constructed using the equations issued from the standard model in a first step. By replacing the absorption, radiation and conduction rates of Eq. 29 by their expression, one obtains the following formulation of the direct problem:

$$\begin{array}{*{20}c} {\underbrace {{\frac{{\pi^{2} \cdot D^{3} \cdot E\left( {m,\lambda_{l} } \right)}}{{\lambda_{l} }} \cdot \frac{{F \cdot q_{\exp } \left( t \right)}}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} q_{\exp } \left( t \right) \cdot {\text{d}}t}}}}_{\text{Absorption}} - \underbrace {{\pi \cdot D^{2} \cdot \mathop \int \nolimits_{0}^{\infty } \frac{{4 \cdot \pi \cdot D \cdot \frac{{\lambda^{{\left( {1 - \xi } \right)}} \cdot \beta }}{6 \cdot \pi }}}{\lambda }.\frac{{2 \cdot \pi \cdot h \cdot c^{2} }}{{\lambda^{5} \cdot \left[ {\exp \left( {\frac{h \cdot c}{{\lambda \cdot k_{B} \cdot T}}} \right) - 1} \right]}} \cdot {\text{d}}\lambda }}_{\text{Radiation}}} \\ { - \underbrace {{\frac{{\pi \cdot D^{2} \cdot \alpha_{T} \cdot p_{0} }}{{R_{p} \cdot T_{g} }} \cdot \sqrt {\frac{{R_{m} \cdot T_{g} }}{{2 \cdot \pi \cdot W_{a} }}} \cdot \left( {c_{p} - \frac{R}{2}} \right) \cdot \left( {T - T_{g} } \right)}}_{\text{Conduction}} - \underbrace {{\left( { - \frac{{\Delta H_{v} }}{{W_{v} }} \cdot \frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)}}_{\text{Sublimation}} = \underbrace {{M \cdot c_{s} \cdot \frac{{{\text{d}}T}}{{{\text{d}}t}}}}_{\text{Internal energy}}} \\ \end{array}$$

(44)

The parameters used for each term are those described in Sect. 2.1 except for E(m, 532) that has been adjusted to a more consistent value of 0.34 following Michelsen [32] and according to the discussion detailed in Sect. 2.3.2. To initiate the iterative loop described in Appendix 1, a diameter temporal evolution issued from the calculations performed with the standard model in Sect. 2 has been implemented as initial guess. At the end of the procedure, a diameter evolution fulfilling the required criteria fixed in the definition of the inverse problem is then obtained and integrated into the Planck function to derive a LII response for each investigated fluence. The obtained temporal profiles of soot diameter and temperature are plotted in Fig. 8a and b for fluences comprised between 0.030 and 0.997 J cm⁻². The evolution of the particle diameter as a function of time and laser energy is consistent with the analysis and comments performed in Sect. 2.3.1. Indeed, an initial slight increase in the particle size is observed during the first nanoseconds following the beginning of the laser pulse due to a decrease in the particle density. Then, the diameter of soot decreases due to sublimation with a decay rate that increases with the fluence. When looking to Fig. 8b, one can note that the soot temperature derived from the energy balance according to Eq. 44 never exceeds the C₂ sublimation temperature even at high fluence. It is, moreover, worthy to note that the general shape of the temperature profile obtained at 0.997 J cm⁻² is close to the one reported by Michelsen in [33] for a fluence of 0.890 J cm⁻² which may indicate similarities between the physical processes taken into account in [33] and those needed to be considered to fit experimental data according to the results of our inverse model (this point will be discussed hereafter). Figure 8c finally illustrates that the simulated LII time decays merge on a single curve with the experimentally monitored signals for all the tested fluences. Such a conclusion is also confirmed by the fluence curve of Fig. 9a. Indeed, simulated data perfectly fit with experimental ones during the monotonic increase in the LII intensity with the laser fluence as well as on the plateau region. By the same way, the agreement between modeled and measured peak temperatures is quite good (see Fig. 9b).

Fig. 8

Results issued from the inverse calculation procedure using the equations from the standard model in the formulation of the direct problem—Evolution of experimental and modeled soot diameter (a), soot temperature (b) and LII signal (c) as a function of time for laser fluences ranging from 0.030 to 0.997 J cm⁻²

Fig. 9

Results issued from the inverse calculation procedure using the equations from the standard model in the formulation of the direct problem—Comparison of experimental and simulated fluence curves (a) and peak soot temperature profiles (b)

That said, if the inverse model leads to define an optimized solution according to the calculation criteria that have been fixed, a thorough analysis of the physical processes involved in the LII phenomenon must be operated, however, to state on the consistency of the obtained results. We therefore plotted in Fig. 10 the temporal evolution of the absorption, radiation and conduction rates (a) as well as the temporal profile of the sublimation flux (b). As expected, the evolution of the absorption, radiation and conduction rates is consistent with results presented in Sect. 2.3.1 (see Fig. 4) since the governing equations accounting for these terms are similar. Nevertheless, one can note that the sublimation flux resulting from the inverse calculation procedure includes a negative part a few nanoseconds after the beginning of the laser pulse. This negative sublimation rate is logically correlated to an increase in the soot mass on the same time scale as observed in Fig. 10c. Such a phenomenon having no physical meaning, a refinement of the calculation procedure has thus been operated to constrain the inverse model in such a way that it cannot predict increases in the mass of soot. Proceeding this way leads to add a complementary energy source term that compensates the negative part of the sublimation rate observed in Fig. 10b.

Fig. 10

Results issued from the inverse calculation procedure using the equations from the standard model in the formulation of the direct problem—Temporal evolution of absorptive heating, radiative and conductive cooling rates (a), evaporative cooling rate (b) and soot mass as a function of time for laser fluences ranging from 0.030 to 0.997 J cm⁻²

At low fluence, the sublimation rate is relatively weak as illustrated in Fig. 4a (the energy balance being dominated by absorption, conduction and radiation rates). In this case, one can easily infer an additional energy flux that is required to fulfill the energy balance of the particle while reproducing the experimental data (see Fig. 11 for a fluence of 0.030 J cm⁻²). Based on the temporal evolution of this complementary energy rate that looks like the profile of the multi-photon absorption flux plotted in Fig. 3a at 0.030 J cm⁻², we tried to approximate it using an equation similar to the one proposed by Michelsen in [32] to account for multi-photon absorption leading to C₂ photodesorption:

$$\phi_{\text{source}} = K_{1} \cdot \pi \cdot D^{3} \cdot \frac{{\left( {B_{\lambda n} } \right)^{n} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} \left[ {q_{\exp } (t)} \right]^{n} \cdot {\text{d}}t}} \cdot \left\{ {1 - \exp \left[ { - \left( {\frac{{F \cdot q_{\exp } (t)}}{{B_{\lambda n} }}} \right)^{n} } \right]} \right\}$$

(45)

where K ₁ is a factor integrating the density of carbon atoms on the surface of the particle and the absorption cross section whose parameterization as given in Sect. 2.1.2 is modified by a scaling factor. The use of such an equation being adapted to fit the inferred energy gain as illustrated in Fig. 11 for a fluence of 0.030 J cm⁻², this leads us to consider by analogy that this additional flux is likely to correspond to a multi-photon absorption process. Such a finding is noteworthy as it supports the insight from Michelsen concerning the relevance of integrating a multi-photon absorption phenomenon in the LII modeling. That said, the sublimation process is strongly active at high fluence as previously noted. The inverse calculation procedure as proposed here is not able to distinguish anymore between the additional absorption and the sublimation contributions as both fluxes have a similar sensitivity toward the assessed problem. Consequently, the complementary absorption rate inferred from the inverse procedure is truncated for times higher than ~12 ns. Nevertheless, using Eq. 45, one can reproduce well the beginning of the temporal profile of the additional source term for fluences higher than 0.080 J cm⁻² as illustrated in Fig. 11. On the other hand, the inclusion of such an energy gain implies to add a complementary loss rate (to be logically related to the removal of carbon clusters by photodesorption) to fulfill the energy balance. The evolutions of the derived energy gain (ϕ _source) and loss (ϕ _loss) rates as a function of time and fluence are plotted in Fig. 12a and b, respectively. Both fluxes present a monotonic increase with the fluence, which can be considered as consistent with processes accounting for multi-photon absorption and nonthermal photodesorption (see Sect. 2.3.1).

Fig. 11

Determination of an additional energy source term from the evaporative cooling rate predicted by the inverse model using equations from the standard model in the formulation of the direct problem

Fig. 12

Time and fluence dependence of the additional energy gain (a) and loss (b) rates derived from the inverse calculation procedure using equations from the standard and refined models in the formulation of the direct problem

This first calculation stage thus illustrated that the sole use of absorption, radiation, conduction and sublimation rates to simulate LII signals is not sufficient to capture thoroughly the detail of soot heating and cooling during the LII phenomenon. The inverse calculation approach adopted here, moreover, provides insights concerning the suitability to include additional energy gain and loss rates that are likely to be attributable to multi-photon absorption and nonthermal photodesorption of carbon clusters as suggested by Michelsen. We therefore operated a second calculation stage (detailed in next section) using the refined model as basis for the definition of the direct problem.

3.2.2 Results obtained using the equations from the refined model in the formulation of the direct problem

The changes to operate in the definition of the direct problem consist in replacing the absorption and sublimation rates of Eq. 44 by the formulations proposed in Eqs. 46 and 47, respectively.

$$\phi_{\text{abs}} = \frac{{\pi^{2} \cdot D^{3} \cdot E\left( m \right)}}{{\lambda_{l} }} \cdot \frac{{f_{1} \cdot B_{\lambda 1} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} q_{\exp } (t) \cdot {\text{d}}t}} \cdot \left\{ {1 - \exp \left[ { - \frac{{F \cdot q_{\exp } (t)}}{{B_{\lambda 1} }}} \right]} \right\}$$

(46)

$$\phi_{\text{sub}} = - \mathop \sum \limits_{j = 1}^{5} \frac{{\varDelta H_{j} }}{{W_{j} }} \cdot \left( {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)_{j}$$

(47)

Following the same methodology as in Sect. 3.2.1, one can infer (using Eq. 45 and as previously illustrated in Fig. 11) the temporal evolution of the additional source term (ϕ _source), which is related to a multi-photon absorption process. The contribution of this term to the global absorption flux is relatively limited at low fluence compared to the single-photon absorption rate while it becomes predominant at high fluence as previously observed when analyzing results obtained with the refined model in Sect. 2.3.1. The corresponding profiles have not been plotted here, however, since observed trends were relatively similar to those depicted in Fig. 3a. The time and fluence dependence of ϕ _source has been plotted in Fig. 12 together with the evolution of the loss rate (ϕ _loss) derived from the energy conservation equation as previously done in Sect. 3.2.1. This procedure leads to define a new direct model whose energy and mass balances can be expressed as follows:

$$ \begin{array}{*{20}c} {\underbrace {{\frac{{\pi^{2} \cdot D^{3} \cdot E\left( m \right)}}{{\lambda_{l} }} \cdot \frac{{f_{1} \cdot B_{\lambda 1} }}{{\int_{0}^{{t_{l} }} {q_{\exp (t)} \cdot {\text{d}}t} }} \cdot \left\{ {1 - \exp \left[ { - \frac{{F \cdot q_{\exp (t)} }}{{B_{\lambda 1} }}} \right]} \right\} + \underbrace {{K_{1} \cdot \pi \cdot D^{3} \cdot \frac{{\left( {B_{\lambda n} } \right)^{n} }}{{\int_{0}^{{t_{l} }} {\left[ {q_{\exp (t)} } \right]^{n} \cdot {\text{d}}t} }} \cdot \left\{ {1 - \exp \left[ { - \left( {\frac{{F \cdot q_{\exp (t)} }}{{B_{\lambda n} }}} \right)^{n} } \right]} \right\}}}_{{\phi_{\text{source}} }}}}_{\text{Absorption}}} \\ { - \underbrace {{\pi \cdot D^{2} \cdot \int\limits_{0}^{\infty } {\frac{{4 \cdot \pi \cdot D \cdot \frac{{\lambda^{{\left( {1 - \xi } \right)}} \cdot \beta }}{6 \cdot \pi }}}{\lambda }} \cdot \frac{{2 \cdot \pi \cdot h \cdot c^{2} }}{{\lambda^{5} \cdot \left[ {\exp \left( {\frac{h \cdot c}{{\lambda \cdot k_{\text{B}} \cdot T}}} \right) - 1} \right]}} \cdot {\text{d}}\lambda }}_{\text{Radiation}} - \underbrace {{\frac{{\pi \cdot D^{2} \cdot \alpha_{T} \cdot p_{0} }}{{R_{p} \cdot T_{g} }} \cdot \sqrt {\frac{{R_{m} \cdot T_{g} }}{{2 \cdot \pi \cdot W_{a} }}} \cdot \left( {c_{p} - \frac{R}{2}} \right) \cdot \left( {T - T_{g} } \right)}}_{\text{Conduction}}} \\ { - \underbrace {{\left\{ { - \sum\limits_{j = 1}^{5} {\frac{{\varDelta H_{j} }}{{W_{j} }} \cdot \left[ { - \frac{{\pi \cdot D^{2} \cdot W_{j} \cdot \alpha_{j} \cdot P_{\text{eq}}^{{c_{j} }} }}{{R_{p} \cdot T}} \cdot \sqrt {\frac{{R_{m} \cdot T}}{{2 \cdot \pi \cdot W_{j} }}} \cdot \frac{{f \cdot k_{p} \cdot T}}{{\sqrt 2 \cdot \sigma_{j} \cdot p_{0} \cdot D \cdot \alpha_{j} + f \cdot k_{p} \cdot T}}} \right]_{{{\text{sub}},j}} + \phi_{\text{loss}} } } \right\}}}_{\text{Sublimation}} = \underbrace {{M \cdot c_{s} \cdot \frac{{{\text{d}}T}}{{{\text{d}}t}}}}_{{{\text{Internal}}\;{\text{energy}}}}} \\ \end{array} $$

(48)

and

$$\frac{{{\text{d}}M}}{{{\text{d}}t}} = \mathop \sum \limits_{j = 1}^{5} - \frac{{\pi \cdot D^{2} \cdot W_{j} \cdot \alpha_{j} \cdot P_{sat}^{{C_{j} }} }}{{R_{p} \cdot T}} \cdot \sqrt {\frac{{R_{m} \cdot T}}{{2 \cdot \pi \cdot W_{j} }}} \cdot \frac{{f \cdot k_{p} \cdot T}}{{\sqrt 2 \cdot \sigma_{j} \cdot p_{0} \cdot D \cdot \alpha_{j} + f \cdot k_{p} \cdot T}}$$

(49)

ϕ _loss has been integrated to the sublimation rate in Eq. 48 as it is assumed to account for the nonthermal photodesorption of carbon clusters. This rate can be expressed as a function of ∆H _λn and k _λn using a formulation for P _λn (derived from the inverse calculation) different from the one described in Sect. 2.1.4. Nevertheless, the formulation of this energy flux as well as the parameterization of the scaling factor integrated in K ₁ is strongly dependent of the choice of the equations and parameters used in the expression of the other energy rates used as baseline terms in the direct problem. As a consequence, additional works including sensitivity analyses to these different parameters as well as complementary calculations performed with other databases are necessary prior to the formulation of a general equation accounting for ϕ _loss. Furthermore and as mentioned in the introduction of this paper, the aim of this first-approach study is not to provide a finalized new LII model but to give insights concerning the most relevant physical processes that should be considered in the modeling procedure. Therefore, we integrated the numerical solutions issued from the inverse model for ϕ _loss in the following calculation steps rather than using an analytical approximate expression which should all the more be viewed with caution as one cannot rule out at this stage that ϕ _loss might correspond to the contribution of different energy loss processes [including thermionic emission, for instance (see Sect. 2.1.7)]. Concerning the mass-balance equation, the B _j factor has been replaced in Eq. 49 by the saturation partial pressure of sublimed clusters (P _λn being issued from the inverse calculation procedure as mentioned above) since the convective contributions to the heat and mass transfer from the particle to the surrounding atmosphere have only little effect on the evaporative cooling rate [33]. Indeed, at temperatures below or well above the sublimation temperature, the evaporative cooling rate is kinetically controlled. On the other hand, the Stefan flux may be significant when the particle temperature reaches values equivalent or just above the sublimation one although such conditions are not maintained over sufficiently long times for the inclusion of the convective transport term to have a substantial effect on the LII temporal profiles.

Proceeding this way, one obtains the temporal profiles of the different energy production and loss terms plotted in Fig. 13 for fluences of 0.030, 0.174 and 0.272 J cm⁻². The temporal evolution of ϕ _loss is of course a bit noisy since such a flux has been inferred from experimental data through an inverse procedure. Compared to results obtained using the refined model (see Fig. 4), we logically find very similar behaviors for absorption, radiation and conduction terms. The energy rate related to the thermal production of carbon clusters is, moreover, relatively weak compared to the photodesorption rate, which is also consistent with predictions issued from the refined model. Besides, the high energy level associated with ϕ _loss in our model and the lower decay rate of such a flux allow fulfilling the particle energy and mass balances without needing the inclusion of a thermionic rate. Results presented here must be analyzed with caution, however, since ϕ _loss may correspond to the cumulative contribution of different energy rates as said above. This being reminded, it appears that the new direct model inferred from the present inverse technique-based work allows reproducing well the experimental data from Gouley et al. as one can see by looking at the LII time decays of Fig. 14a, the corresponding evolution of soot temperature and diameter as a function of time being proposed in Fig. 14b and c for illustration purposes and potential further uses. By the same way, the simulated fluence curve and the peak soot temperature profile (not shown here as they are quite identical to those presented in Fig. 9) are perfectly consistent with experimental measurements. Finally, we also plotted in Fig. 15 the soot temperature temporal profiles calculated for fluences of 0.1 (a) and 0.8 J cm⁻² (b) together with the corresponding experimental temperature decay rates measured in [44] using spectrally resolved LII and three-color LII. Obtained results illustrate a globally good agreement (considering the measurement uncertainty range) between simulated and measured temperatures at low/intermediate fluence (see Fig. 15a). On the other hand, the agreement is less satisfactorily at high fluence (0.8 J cm⁻²) although such a trend can be correlated to an experimental artifact as pointed out by Gouley et al. [44]. According to these authors, the second temperature rise observed on experimental curves of Fig. 15b corresponds to a tail in the collected LII profiles that has been identified as being laser-induced fluorescence (LIF) signals of large molecules present in the investigated flame. Once the soot is vaporized and the LII signal has dropped, such LIF emissions as well as C₂ and C₃ interferences contribute to the collected light leading to experimental artifacts when fitting a Planck function to the total emitted signal or when inferring soot temperature by multi-color LII (especially since one of the collection wavelength has been selected at 451.5 nm). Thus, if predicted data logically diverge from the anomalous high temperatures (>4,500 K) experimentally determined for times higher than 10 ns, it is worthy to note that the model, however, captures a second temperature rise for an identical time scale. Such a phenomenon is related in our calculation to the additional quantity of energy absorbed by the particle through the assumed multi-photon process (ϕ _source) and to the subsequent competition between absorption and evaporative cooling rates (including ϕ _loss) at high fluence. ϕ _source and ϕ _loss being attributed to multi-photon absorption leading to the subsequent nonthermal photodesorption of carbon clusters, the specific behavior in the temporal evolution of the soot temperature could be possibly related to the balance between such photolytic mechanisms, which would be consistent with the high C₂ interferences observed by Gouley et al. [44] during the multi-color LII measurements at 532 nm. This would also be consistent with the fact that such a phenomenon is not observed at 1,064 nm as the absorption coefficient and the efficiency of photodesorption are lower for such a wavelength assuming a three- to four-photon process [88]. Such an analysis (postulating that the secondary temperature rise experimentally monitored by Gouley et al. could be due not only to an artifact) is of course hypothetical and must be considered with caution especially since the model used here is issued from an inverse calculation procedure, which can be biased by experimental uncertainties or measurement noise/interferences (though LII time decays measured by Gouley et al. and modeled here are supposed to be interference-free as explained in [44]). Besides, the experimentally measured time-resolved LII signals at high laser fluences are also likely to be deformed from the true ones due to the finite response of the detectors used, which may then influence the soot thermal history inferred from the energy balance equated based on the results of the inverse calculations. On the other hand, similar features have already been reported in other works and related to a possible secondary heating of soot by scattered light [89] or to incandescence from particles generated from sublimed carbon clusters [88], thus stimulating further investigations to better interpret such a specific observation. One can finally note, based on temperature profiles of Figs. 14b and 15, that the new direct model predicts well a plateau in the maximum soot temperature for fluences above 0.2 J cm⁻². Such a behavior contrasts with predictions issued from a majority of LII models proposed in the literature (as illustrated in Sect. 2.3, for instance), thus demonstrating the large uncertainties in existing models especially at intermediate and high fluences. This also indicates the absence of substantial superheating, which is an important feature of the present work as such a trend is consistent with experimental observations from Gouley et al. [44].

Fig. 13

Temporal evolution of energy heating and cooling rates from the new direct model for fluences of 0.030, 0.174 and 0.272 J cm⁻²

Fig. 14

Predicted evolution of LII signal (a), soot temperature (b) and soot diameter (c) as a function of time for laser fluences ranging from 0.030 to 0.997 J cm⁻² using the new direct model. Modeled LII time decays are plotted together with measured ones on (a)

Fig. 15

Comparison of temperature temporal profiles modeled using the new direct model and measured in [44] by the means of spectrally resolved LII and three-color LII for fluences of 0.1 (a) and 0.8 J cm⁻² (b)

4 Conclusion

Two LII models issued from the literature have been tested in order to simulate experimental data collected by Gouley et al. [44] in a non-smoking laminar diffusion flame of ethylene using a 532-nm laser source presenting smooth temporal and homogeneous spatial profiles. The first model (called “standard model”) has been derived from the extensively used formulation proposed by Melton [9] and accounts for particle heating by absorption and cooling by radiation, sublimation and conduction. The second model (referenced as “refined model”) has been derived from the formulation proposed by Michelsen [32, 33] and integrates an alternative formulation of the absorption term that accounts for saturation of the linear, single-photon and multi-photon absorption, a contribution related to the photodesorption of C₂ carbon clusters in the evaporative cooling rate, a heating flux attributable to oxidation and a cooling process based on thermionic emission in addition to the usual conduction and radiation cooling fluxes.

Obtained results illustrated that both models fail to reproduce the LII signals experimentally monitored by Gouley et al. over a wide range of fluences (up to ~1 J cm⁻²). No fit between theoretical and measured data has been obtained regardless of the value of the main parameters involved in the energy- and mass-balance equations. Such a conclusion has been supported by a sensitivity analysis focusing on the LII response dependence to parameters like the soot refractive index function E(m, λ) and the thermal accommodation coefficient α _T . Despite the absence of agreement between measured and modeled data, the refined model has been shown to reproduce well the lack of fluence dependence of the peak LII signal above the sublimation threshold. Such an interesting feature is related to the inclusion of the multi-photon absorption process, leading to the photodesorption of C₂ clusters at high fluence. Taking into account such processes into the calculation did not allow predicting peak soot temperatures consistent with experimentally measured ones, however, prompting demand for additional investigations to be conducted.

Based on such a conclusion, we proposed a new modeling approach based on the use of inverse techniques so as to gain information about specific terms that should be integrated in the calculation procedure. The strategy adopted in this work is based on a nonlinear optimization problem the resolution of which has been achieved using a variable metric method integrating the BFGS formulation for the definition of the positive-definite approximation of the Hessian matrix and the Armijo rule for the determination of the optimal step size. The implementation of such an inverse calculation procedure allows determining the temporal evolution that should be followed by the soot diameter so as to minimize the difference between LII responses simulated using a baseline direct model and experimentally monitored signals. Based on the analysis of obtained results, one can infer the temporal and fluence dependence of additional energy rates that have to be considered to fulfill the particle energy and mass balances while providing the best agreement with experimental data.

Conclusions issued from a first calculation stage illustrated that modeling soot LII using only absorption, radiation, conduction and sublimation rates (as these fluxes are generally expressed and computed in the literature) was inadequate to correctly simulate the soot heating and cooling mechanisms over a wide range of fluences. The inverse modeling procedure also demonstrated the necessity to include additional energy gain (ϕ _source) and loss (ϕ _loss) rates to be able to reproduce experimental data provided in [44]. The additional energy flux contributing to the particle heating (ϕ _source) has been related to a multi-photon absorption process based on its temporal and fluence dependence. Such a finding is of interest as it supports the insight from Michelsen concerning the relevance of integrating such a phenomenon in the LII modeling. The energy loss rate has been assigned, for its part and among other, to a nonthermal photodesorption process, leading to the emission of carbon clusters. Additional calculations performed using equations derived from the refined model led to define a new direct model integrating ϕ _source (which follows an equation similar to the one proposed by Michelsen in [32] for multi-photon absorption but with a different parameterization) and ϕ _loss (whose temporal evolution as a function of the fluence has been provided in this paper for further modeling work). Predictions issued from this new direct model have been found to merge on a single curve with experimental data.

Additional works need to be undertaken, however, to complete and refine the results and conclusions issued from the present baseline study. First of all, the formulation and the parameterization of the additional energy fluxes that have been inferred from the inverse calculation procedure are directly influenced by the choice of the equations and parameters used in the expressions accounting for the other energy rates integrated in the energy- and mass-balance equations. As a consequence, complementary investigations including sensitivity analyses to such factors should be carried out using additional data sets to propose refined expressions for ϕ _source and ϕ _loss valid on an extensive range of conditions. Besides, through the key avenues identified in this work, multi-photon absorption and photolytic mechanisms leading to the nonthermal emission of carbon clusters have been shown to be among the most relevant to be addressed. Coupling new modeling approaches like the one proposed in this study with thoroughly obtained experimental data (as those issued from [88]) should be of interest to gain a better understanding of such physical mechanisms that may strongly influence the LII response. Finally, investigations already in progress in our laboratory also focus on the inclusion in the inverse calculation procedure of the effect of multiple scattering that is likely to influence the radiative properties of the soot fractal aggregates [90] as well as the impact of annealing [33] and coating [91], which can significantly interfere in the energy balance of the particle. Such additional studies conducted using the original approach proposed in this paper should be of help to improve predictions issued from future LII models.

Appendices

Appendix 1: Algorithm of the inverse calculation procedure

The algorithm describing the iterative process implemented to solve the inverse problem can be summarized as follows:

Step 1: Start with an initial guess for $\left( {D_{k = 0} = \left[ {D_{1} , D_{2} , \ldots ,D_{i} , \ldots , D_{{N_{t} }} } \right]^{T} } \right)$ and with a (N _t  × N _t ) positive-definite symmetric matrix H _κ=0. Usually H _κ=0 is taken as the identity matrix I. For D _k=0, the solution obtained using one of the models implemented in Sect. 2 is considered.

Step 2: Solve the direct problem described by Eq. 29 to obtain the time-dependent temperature and compute the LII signal based on Eq. 28.

Step 3: Compute the gradient of the cost function using Eq. 38, the direction of descent based on Eq. 33 and the sensitivity coefficients for each component of the unknown vectors $\left( {D_{k} = \left[ {D_{1} , D_{2} , \ldots ,D_{i} , \ldots , D_{{N_{t} }} } \right]^{T} } \right)$ using the formulation proposed in Eq. 40.

Step 4: Find the optimal step size η _κ by solving the iterative inexact line search problem based on the Armijo rule given by Eq. 41.

Step 5: Calculate the new estimation for the diameter D _κ+1 using Eq. 31.

Step 6: Test the new estimation for optimality (stopping criterion). If D _κ+1 is optimal, terminate the iteration process. Otherwise, go to next step.

Step 7: Update H _κ+1 based on the BFGS formula (Eq. 37).

Step 8: Set the new iteration number κ = κ + 1 and go to step 2.

Appendix 2: Nomenclature

B λ1	Empirically determined saturation coefficient for linear absorption	(J cm−2)
B λn	Empirically determined saturation coefficient for multi-photon absorption	(J cm−2)
c	Speed of light	(cm s−1)
c s	Specific heat of solid carbon (graphite)	(J g−1 K−1)
C p	Molar heat capacity for ambient gases at constant pressure	(J mol−1 K−1)
C v	Molar heat capacity for ambient gases at constant volume	(J mol−1 K−1)
C CO p	Molar heat capacity of CO	(J mol−1 K−1)
C abs	Absorption cross section for soot particles in the Rayleigh regime	(cm2)
D	Primary particle diameter	(cm)
D eff	Total effective diffusion constant	(cm2 s−1)
d	Direction of descent	(–)
E(m)	Dimensionless refractive index function	(–)
F	Laser fluence	(J cm−2)
f	Dimensionless Eucken correction to the thermal conductivity of polyatomic gas	(–)
f 1	Empirical scaling factor for linear absorption	(–)
G	Geometry-dependent heat transfer factor	(–)
H	Approximation of the Hessian matrix	(–)
h	Planck constant	(J s)
I	Identity matrix	(–)
i	Time step index	(–)
k B	Boltzmann constant	(J K−1)
k p	Boltzmann constant in effective pressure units	(bar cm3 K−1)
k ox	Overall rate constant for oxidation	(s−1 cm−2)
k λn	Rate constant for removal of C 2 by photodesorption	(s−1)
Kn	Knudsen number	(–)
L c	Characteristic length	(cm)
M	Particle mass	(g)
m e	Mass of an electron	(J s2 cm−2)
n	Estimated number of 532-nm photons absorbed to photodesorb C 2	(–)
n g	Number density of gas molecules	(cm−3)
N A	Avogadro constant	(mol−1)
N ss	Density of carbon atoms on the surface of the particle	(cm−2)
N t	Total number of discrete time steps	(–)
p 0	Ambient pressure	(bar)
p v	Average partial pressure of sublimed carbon species	(bar)
P ref	Reference pressure	(bar)
$P_{\text{eq}}^{{C_{j} }}$	Thermal equilibrium partial pressure of C j	(bar)
$P_{\text{sat}}^{{C_{j} }}$	Saturation partial pressure of C j	(bar)
$P_{\text{surf}}^{{C_{j} }}$	Partial pressure of C j at the particle surface	(bar)
P λn	Effective pressure calculated from the rate of photodesorption of C 2	(bar)
q	Probe laser irradiance	(W cm−2)
q exp	Experimental temporal profile of the laser	(Arbitrary unit)
R	Universal gas constant	(J mol−1 K−1)
R m	Universal gas constant in effective mass units	(g cm2 mol−1 K−1 s−2)
R p	Universal gas constant in effective pressure units	(bar cm3 mol−1 K−1)
SLII	Calculated LII signal	(Arbitrary unit)
SLII*	Measured LII signal	(Arbitrary unit)
t	Time	(s)
t f	Final measurement time	(s)
t l	Laser pulse duration	(s)
T	Particle temperature	(K)
T g	Ambient gas temperature	(K)
$T_{\text{ref}}^{{C_{j} }}$	Reference temperature for C j	(K)
W 1	Average molecular weight of atomic carbon	(g mol−1)
W a	Average molecular weight of air	(g mol−1)
W v	Average molecular weight of sublimed carbon species	(g mol−1)
W j	Molecular weight of C j (j × 12.011)	(g mol−1)
${\mathcal{J}}$	Objective (or cost) function	(Arbitrary unit)
${\mathcal{R}}_{\lambda \det }$	Spectral characteristics of the detection system	(Arbitrary unit)
${\mathcal{X}}$	Sensitivity coefficient	(Arbitrary unit)
α j	Mass accommodation coefficient of vaporized species C j	(–)
α M	Species-independent mass accommodation coefficient of vaporized carbon clusters	(–)
α T	Thermal accommodation coefficient of ambient gases with the surface	(–)
β	Scaling factor for emissivity	(–)
γ	Heat capacity ratio for the ambient gas surrounding the particles	(–)
ΔH j	Enthalpy of formation of carbon vapor species C j	(J mol−1)
ΔH v	Average enthalpy of formation of sublimed carbon species C j	(J mol−1)
ΔH ox	Enthalpy of reaction for 2C + O2 → 2CO	(J mol−1)
ΔH λn	Enthalpy required to photodesorb C 2	(J mol−1)
Δλ det	Spectral range of the detection system	(cm)
ɛ λ	Emissivity at wavelength λ	(–)
ϵ	Real number used to calculate the sensitivity coefficient	(–)
η	Search step size	(–)
κ	Iteration index	(–)
κ a	Thermal conductivity of the surrounding gases	(W cm−1 K−1)
λ	Wavelength	(cm)
λ l	Laser wavelength	(cm)
λ g	Mean free path of gas molecules	(cm)
ξ	Dispersion exponent	(–)
ρ s	Density of graphite	(g cm−3)
σ	Average molecular cross section for ambient gases	(cm2)
$\bar{\sigma }$	Average molecular cross section for sublimed species	(cm2)
σ err	Standard deviation of the measurement errors	(Arbitrary unit)
σ j	Molecular cross section for sublimed species C j	(cm2)
σ λn	Empirically determined multi-photon absorption cross section for photodesorption of C 2	(Cm2n−1 J1−n)
ϕ	Work function	(J)
ϕ abs	Rate of energy gained by laser absorption	(W)
ϕ cnd	Rate of energy lost by conduction to the surrounding gases	(W)
ϕ int	Rate of change of the internal energy of the particle	(W)
ϕ loss	Additional rate of energy lost by the particle (inferred from the inverse model)	(W)
ϕ ox	Rate energy gained by oxidation of the particle	(W)
ϕ rad	Rate of energy lost by radiative emission	(W)
ϕ source	Additional rate of energy gained by the particle (inferred from the inverse model)	(W)
ϕ sub	Energy loss rate due to the sublimation mechanism	(W)
ϕ th	Energy loss rate by thermionic emission	(W)
ω	Tolerance used in the Armijo rule	(–)
∇	Gradient	(–)
∇2	Hessian matrix	(–)