1 Introduction

In recent years, many researchers aiming on high-power and high-energy laser operation have paid more attention to coherent beam combination (CBC). CBC has many advantages not only to obtain higher powers, but also for high beam quality, leading to remarkable achievements in high-power and high-brightness lasers.

In CBC, it is essential to actively lock phases of the beam components to be combined, in order to combine them constructively. A variety of methods can be used to lock the phases of the beam components such as heterodyne beam combination [1, 2], stochastic parallel gradient decent (SPGD) algorithm phase locking [3, 4], and locking of optical coherence via single-detector electronic-frequency tagging (LOCSET) [5–7]. Among those, the LOCSET technique has shown great progress in terms of high power and large scalability of beams. This technique was proposed by Dr. Thomas Shay in 2006 and demonstrated in the same year [5, 6]. Through this technique, people can combine a large amount of fiber beam sources with only a single detector. In experiments using the LOCSET technique, 5-channel beam combination systems have recorded an RMS phase error of approximately λ/60 [7]. This is why the LOCSET technique has been employed by many researchers aiming to obtain high-power and high-energy lasers.

Thus far, the LOCSET technique has been demonstrated with electro-optic modulators (EOMs) such as LiNbO3 since they give a high ac modulating frequency resulting in a high-control bandwidth. However, as the power of the beam components increases, the usage of an EOM has limitations because of its high insertion loss and low laser-induced damage threshold [8].

PZT tubes are good alternatives to EOMs as phase modulators in CBC. PZT tubes have several advantages over EOMs, such as of little loss, high-damage threshold, and low costs. However, since tube type PZT has a narrow linear frequency response range of several tens of kHz, resulting in a poor control bandwidth, they are rarely used in CBC systems. To overcome this limitation, we improved the theory of the LOCSET technique by determining an integration time as the least common multiple of modulating frequencies, allowing us to keep the original high performance merits of the LOCSET technique, while achieving a high-control bandwidth with PZT tubes. This M-LOCSET theory makes it possible to set a simple and efficient experimental scheme for combining a large number of higher-power lasers as well as to drastically reduce its costs.

2 The modified LOCSET theory

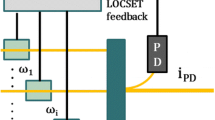
Assuming self-synchronous LOCSET [5], the electric field of the ith modulated beam Ei is,

$$E_{i} (t) = E_{i0} \cdot \cos (\omega_{\text{L}} t + \phi_{i} + \beta_{i} \sin (\omega_{i} t)),$$
(1)

where E i0 represents the field amplitude for the ith modulated beam and ω i represents the radio frequency (RF) for the ith modulated beam. ω L and ϕ i represent laser frequency and optical phase of ith beam, respectively.

Substituting the trigonometric identity for the cosine of the sum of the optical phase and the phase-modulating term into Eq. (1),

$$E_{i} (t) = E_{i0} \cdot \left[ {\begin{array}{*{20}c} {\cos (\omega_{\text{L}} t + \phi_{i} )\cos (\beta_{i} \sin (\omega_{i} t))} \\ { - \sin (\omega_{\text{L}} t + \phi_{i} )\sin (\beta_{i} \sin (\omega_{i} t))} \\ \end{array} } \right].$$
(2)

The photocurrent i PD detected at the photodiode is expressed as an interference signal between modulated beams:

$$i_{PD} = R_{PD} \cdot A \cdot \sqrt {\frac{{\mu_{0} }}{{\varepsilon_{0} }}} \cdot \left( {\sum\limits_{i = 1}^{N} {E_{i} (t)} } \right)\left( {\sum\limits_{j = 1}^{N} {E_{j} (t)} } \right),$$
(3)

where N represents the number of modulated beams and i and j represent the summation indices of each modulated beam. μ 0 and ε 0 represent the magnetic and electric permeabilities of free space, respectively, and R PD and A represent the responsivity and the active area of the photodetector, respectively.

Skipping the complex calculation, we focus on getting the cth phase signal for phase locking. The cth phase error signal Sc that we are interested in can be obtained by demodulating the photocurrent iPD for the cth modulating frequency ωc, yielding:

$$S_{c} = \frac{1}{\tau }\int\limits_{0}^{\tau } {i_{\text{PD}} (t) \cdot \sin (\omega_{c} t)dt,}$$
(4)

In the original LOCSET theory, when ω i  = ω c it is required that integration time τ should be far longer than 2π/ω i and τ ≫ 2π/|ω i  − ω j | for all i and j when j ≠ i, so that the Eq. (4) fulfills the sine and cosine orthogonalities and is approximated as a simple expression. This expression is then:

$$S_{i} = R_{\text{PD}} \cdot \sqrt {P_{i} } \cdot J_{1} (\beta_{i} ) \cdot \sum\limits_{j = 1}^{N} {\sqrt {P_{j} } \cdot J_{0} (\beta_{j} ) \cdot sin(\varphi_{j} - \varphi_{i} )} ,$$
(5)

where φ j and φ i represent the phases of the jth and ith phase modulated beam, respectively. P i represents the optical power of the ith modulated beam:

$$P_{i} = \frac{{A \cdot E_{i0}^{2} }}{2}\sqrt {\frac{{\mu_{0} }}{{\varepsilon_{0} }}} .$$
(6)

The above time requirement limits the control bandwidth of the phase-locking system. When using phase modulators with high modulating frequencies such as EOMs, this problem is not critical as they have high bandwidths. When PZT tubes are used as phase modulators, however, the control bandwidth is limited since PZT tubes only have a linear frequency response at 0–20 kHz [8].

Fortunately, this problem can be easily solved by choosing the acquisition frequency f (the inverse of the integration time τ) as the least common multiple of modulating frequencies. In this case, we can get Eq. (5) with only a short integration time τ, resulting in a much higher-control bandwidth over than with the original LOCSET method.

For instance, if we adopt the modulating frequencies as about 8, 6, 4, and 2 kHz, we must have τ satisfying the conditions 2π/ω i and τ ≫ 2π/|ω i  − ω j |, i.e., τ ≫ 3 ms, in order to fulfill the orthogonalities. Therefore, τ should be several tens to several hundreds of milliseconds in accordance with the original LOCSET theory. On the other hand, in the M-LOCSET theory (illustrated in Fig. 1), τ could be about 0.5 ms, which is much faster than in the original LOCSET method.

Fig. 1
figure 1

Integration time τ, determined by the least common multiple of the modulating frequencies (8,333, 6,250, 4,167, 2,083 Hz), where the sampling frequency is 250 kHz

Full size image

Through the M-LOCSET theory, PZT tubes can be used to lock the phases of each beam component in CBC system, leading to a high-control bandwidth as well as solving the problems of high insertion loss and a low-damage threshold caused by EOMs. In the next section, the feasibility of the M-LOCSET theory with PZT tubes is demonstrated by combining four coherent beams.

3 Experimental setup and results

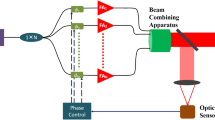
To measure the performance of this system, amplifier-like noises are added to each fiber beam component by using PZT tubes instead of using real fiber amplifiers. Figure 2 shows the experimental setup of the noise-generated four-beam combination and phase control with the M-LOCSET technology.

Fig. 2
figure 2

Experimental setup of four-beam combination with the M-LOCSET technology. All components are polarization maintaining (PM). First four PZT tubes are used as fiber amplifiers in order to make amplifier-like noises on each beam. Second four PZT tubes perform functions of phase modulation and feedback

Full size image

A beam from a 1,550 nm polarization-maintaining (PM) distributed feedback (DFB) fiber laser with a maximum power of 1 W, is divided into four subbeam components, by passing through a one-by-four beam coupler (which is also a PM component). A generated noise and phase modulation are then added to each beam component via PZT tubes, whose fibers are strengthened and loosened by the piezoelectric effect. Both the noise and modulation signals are generated by a computer-based data acquisition (DAQ) board and analog output (AO) board. Finally, each beam component is combined to one beam through a one-by-four PM coupler, and the combined beam is directed onto the photodiode (PD). As a result, phase differences between the beam components are calculated by the above Eq. (5), and the proportional feedback signals are given to the beams, locking the phases. In this case, the sampling frequency of the DAQ board is 250 kHz, and the integration time is the reciprocal of 2,083 Hz, the least common multiple of the modulating frequencies.

The creation of the given noises is based on noises measured in 10 W and higher amplifier systems [9, 10]. Since phase noise depend weakly on signal power, and they have almost the same distributions for fiber lasers with 5 and 608 W output power [8, 11], the given noises are expected to have almost same amount of influence as that of high-power amplifiers on the beam components.

The intensity signals of the combined beam detected by the PD are shown in Fig. 3. It can be seen that the normalized intensity signal of the combined beam randomly fluctuates between 0 and 1 in the open loop, while remaining around 1 in the closed loop. When the loop is closed, the residual phase error of the beam components was recorded as around λ/24, which satisfies the phase matching tolerance of λ/20 [12]. Figure 4 shows that the power spectral density in the closed loop is far lower than in the open loop below 100 Hz.

Fig. 3
figure 3

Intensity signals of the combined beam in the open loop (left) and closed loop (right) in time domain

Full size image
Fig. 4
figure 4

Power spectral density in the open loop (black) and the closed loop (red) in frequency domain

Full size image

However, it is difficult to gain the control bandwidth of this system through Fig. 4 at a glance. To gain the exact control bandwidth of this system, we calculated structure function which is defined as below:

$${\text{SF}} = \left\langle {\left| {\varphi (t + \tau ) - \varphi (t)} \right|} \right\rangle ,$$
(7)

which can quantify the amount of phase fluctuation accumulated in time [10]. The structure function in this system calculated as Fig. 5.

Fig. 5
figure 5

Structure function in the open loop

Full size image

As shown in Fig. 5, the control bandwidth of this system should be more than 100 Hz to accomplish the λ/20 of residual phase error, which is the requirement of phase matching tolerance. Since the residual phase error of this system was calculated as λ/24, less than λ/20, it is concluded that the control bandwidth of this system is higher than 100 Hz. According to this result, it is expected that this system could be employed to combine beams in CBC system using high-power amplifiers.

4 Conclusion

In summary, the M-LOCSET theory with PZT tubes as phase modulators was presented and demonstrated experimentally by combining four fiber beams. To prove the performance of this system, we generated phase noises given by high-power amplifiers and added them to each beam component and measured the phase stability and control bandwidth of the combined beams. Consequently, in the closed loop, the residual phase of λ/24 has been obtained and the control bandwidth is much higher than 100 Hz. We anticipate that it gives us much higher-control bandwidth to apply a field programmable gate array (FPGA) chip than to apply the DAQ board. The M-LOCSET theory presented here will allow PZT tubes to be more powerful tools than EOMs in the high-power CBC.