1 Introduction

Diode-pumped alkali lasers (DPALs), first demonstrated in 2005, have garnered considerable attention in recent years because of their potential for the realization of a high-powered laser [1–4]. As a novel type of hybrid laser, DPALs offer a number of advantages compared to other types of high-powered lasers [5–7]. As the quantum defect is extremely low (4.72 % for Cs, 1.85 % for Rb, and 0.44 % for K), it is possible to construct a laser with both high optical-to-optical efficiency and facile thermal management [8, 9]. The thermal difficulties associated with such a laser can be further alleviated in a DPAL by removing waste heat through the flowing gain medium [10–12]. In addition, the recycling time of an alkali atom in the lasing process in a DPAL can be very short, on the order of 100 ps [13]. These advantages make DPALs one of the most promising candidate technologies for high-powered lasers with both good beam quality and a compact size [14]. Recently, Russian researchers have achieved an output power of approximately 1 kW in a cesium laser with a two-side pumped configuration [15]. They report an optical-to-optical efficiency of as high as 48 %.

To date, numerous theoretical and experimental studies of DPALs have been undertaken by laser scientists [16, 17]. However, most of these studies have addressed only output performances. Although a few studies have been reported in regarding the characteristics of DPALs in time domain, the detailed analyses of relaxation oscillation (RO) generation still keep infrequent at present [18–21]. RO is a phenomenon that involves energy exchanges in the time domain between population inversion and cavity photons for optical oscillation [22]. Since the first ruby laser was invented by T. H. Maiman in 1960, ROs in many types of lasers have been extensively investigated to study the dynamic process in the time domain [23–27]. One common application of RO is the generation of a single laser mode (SLM) through self-seeding with a pre-laser signal in a solid-state laser [28]. Another practical application of RO is the measurement of various laser parameters, such as the spontaneous lifetime and cavity losses [29, 30]. However, the generation of spikes in ROs may pose an obstacle to the establishment of stable oscillation, especially when the laser cavity is short [31, 32].

It is important to note that two unique features of DPALs set them apart from conventional solid-state lasers. First, the recovery time of the excited population inversion is extremely short because the decay rate of the upper level of a stimulated alkali atom is much higher than those of almost all solid-state lasers [33]. Secondly, the transient effect in DPALs may cause serious fluctuations in output irradiation, as the gain in a DPAL is often very high [34]. In fact, the two regimes mentioned above can be correlated with the RO behaviors in a laser oscillator. It is reasonable to suppose that RO processes might somewhat affect the output features of a DPAL. Therefore, an investigation of the RO phenomena in a DPAL should facilitate the understanding of the underlying physical mechanism of laser generation. In this paper, we first investigate the output characteristics in the time domain using the time-dependent laser rate equations and then present a detailed study of ROs in a DPAL. We believe the results should be useful for the suppression of output noise and the design of a stable DPAL source.

2 Theoretical analyses using a kinetic model

In this section, we develop a kinetic model to analyze the characteristics of RO for an end-pumped diode-pumped rubidium laser. Methane and helium are chosen as the buffer gases. Note that the quenching of upper-level spin–orbit states and the shift in the center wavelength of the D2 line that arises because of the use of two types of buffer gases are both considered in the calculation. Because the fluctuation in output intensity for a DPAL is related to spontaneous emission, we also investigate the influence of spontaneous emission on the laser output in the kinetic model.

2.1 Examination of the features of an end-pumped DPAL in the time domain

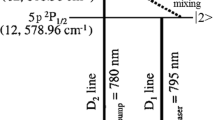
As a three-level laser, the DPAL is pumped on the D2 transition, 2S1/2 → 2P3/2, and lased on the D1 transition, 2P1/2 → 2S1/2. The electronic energy levels of rubidium atoms pumped by laser diodes are illustrated in Fig. 1. γ32 is the fine-structure mixing rate related to the speed of relaxation from the 2P3/2 level to the 2P1/2 level. A and Q represent the spontaneous emission rate and the quenching rate, respectively. n 1(t), n 2(t), and n 3(t) are the alkali number densities at the 2S1/2, 2P1/2, and 2P3/2 levels, respectively.

Fig. 1
figure 1

Energy-level diagram and major kinematic processes for a diode-pumped rubidium vapor laser

Full size image

In this study, all number densities of the three levels are assumed to remain unchanged in geometry inside the vapor cell for mathematical simplicity. The model is formulated in terms of the pump-photon absorption rate Γ P(t) and the longitudinally averaged two-way laser intensity Ψ(t). Thus, we can determine the rate equations that describe the population densities of the 2S1/2, 2P1/2, and 2P3/2 levels as well as the longitudinally averaged two-way laser intensity in the time domain as follows:

$$\begin{aligned} \frac{{{\text{d}}n_{1} (t)}}{{{\text{d}}t}}\; & = \; - \varGamma_{\text{P}} (t) + \sigma_{21} \left( {n_{2} (t) - n_{1} (t)} \right)\frac{\varPsi (t)}{{h\nu_{21} }} + n_{2} (t) \times \left( {A_{21} + Q_{21} } \right) + n_{3} (t) \times \left( {A_{31} + Q_{31} } \right) \\ \frac{{{\text{d}}n_{2} (t)}}{{{\text{d}}t}} & = - \sigma_{21} \left( {n_{2} (t) - n_{1} (t)} \right)\frac{\varPsi (t)}{{h\nu_{21} }} + \gamma_{32} \left[ {n_{3} (t) - 2n_{2} (t) \times \exp \left( { - \frac{\Delta E}{{k_{\text{b}} T}}} \right)} \right] - n_{2} (t) \times \left( {A_{21} + Q_{21} } \right) \\ \frac{{{\text{d}}n_{3} (t)}}{{{\text{d}}t}} & = \varGamma_{\text{P}} (t) - \gamma_{32} \left[ {n_{3} (t) - 2n_{2} (t) \times \exp \left( { - \frac{\Delta E}{{k_{\text{b}} T}}} \right)} \right] - n_{3} (t) \times \left( {A_{31} + Q_{31} } \right) \\ n_{0} & = n_{1} (t) + n_{2} (t) + n_{3} (t) \\ \frac{{{\text{d}}\varPsi (t)}}{{{\text{d}}t}} & = \left( {{\text{TT}}^{2} R_{\text{oc}} \exp \left[ {2L_{\text{g}} \sigma_{21} \left( {n_{2} (t) - n_{1} (t)} \right)} \right] - 1} \right)\frac{\varPsi (t)}{{t_{\text{RT}} }} + \varPsi_{1} (t), \\ \end{aligned}$$
(1)

where σ 21 is the stimulated emission cross section for the lasing transition evaluated at the center of the line, which is broadened by the buffer gases in the cell; ∆E is the energy gap between the 2P3/2 and 2P1/2 levels; k b is the Boltzmann constant; T is the cell temperature; TT is the one-way cavity transmittance at the lasing wavelength; R OC is the reflectance of the output coupler; L g is the length of the gain medium; t RT is the round-trip time for the laser cavity; Ψ 1(t) is the spontaneous emission density coupled with the lasing mode [35], which will be discussed in the next subsection; and n 0 is the total alkali number density in the cell, which can be expressed as a function of the cell temperature [36]:

$$n_{0} = \frac{133.322}{{k_{\text{b}} T}} \times 10^{{2.881 + 4.312 - \frac{4,040}{T}}} .$$
(2)

The fine-structure mixing rate increases after the addition of the buffer gases, methane and helium, as described by

$$\gamma_{32} = n_{\text{methane}} \;V_{\text{r}}^{{{\text{Rb}} - {\text{methane}}}} \sigma_{\text{methane}} + n_{\text{He}} \;V_{\text{r}}^{{{\text{Rb}} - {\text{He}}}} \sigma_{\text{He}} ,$$
(3)

where n methane and n He represent the number densities of methane and helium inside the cell, respectively. σ methane and σ He are the fine-structure mixing cross sections of methane and helium, respectively, and they are assumed to remain constant with varying temperature in the computation. V Rb–methaner and V Rb–Her are the rms thermally averaged relative velocities between the rubidium atoms and the methane molecules and helium atoms, respectively, as expressed below:

$$\begin{aligned} V_{\text{r}}^{{{\text{Rb}} - {\text{methane}}}} & = \sqrt {3k_{\text{b}} T\left( {\frac{1}{{m_{\text{Rb}} }} + \frac{1}{{m_{\text{methane}} }}} \right)} \quad \\ V_{\text{r}}^{{{\text{Rb}} - {\text{He}}}} & = \sqrt {3k_{\text{b}} T\left( {\frac{1}{{m_{\text{Rb}} }} + \frac{1}{{m_{\text{He}} }}} \right)} , \\ \end{aligned}$$
(4)

where m Rb, m He and m methane are the masses of a rubidium atom, a helium atom, and a methane molecule, respectively.

The quenching rate Q 31 is also determined by the composition of the buffer gases as follows:

$$Q_{31} = n_{\text{methane }} V_{\text{r}}^{{{\text{Rb}} - {\text{methane}}}} \sigma_{\text{quenching}}^{\text{methane}} + n_{\text{He}} V_{\text{r}}^{{{\text{Rb}} - {\text{He}}}} \sigma_{\text{quenching}}^{\text{He}} ,$$
(5)

where σ methanequenching and σ Hequenching are the quenching cross sections corresponding to methane and helium, respectively. Because the energy gap between the 2P3/2 and 2P1/2 levels is quite narrow, the value of Q 21 is assumed to be equal to that of Q 31.

For an end-pumped DPAL with a double-pass pump structure, as illustrated in Fig. 2, Γ P can be expressed as [7]

$$\begin{aligned} \varGamma_{\text{P}} (t) & = \frac{{\eta_{\text{mode}} \eta_{\text{del}} }}{{V_{\text{L}} }}\int {\frac{\lambda }{hc}} P_{\text{p}} (\lambda ) \times \left\{ {1 - \exp \left[ { - \left( {n_{1} (t) - \frac{{n_{3} (t)}}{2}} \right)\sigma_{\text{D2}} (\lambda )L_{\text{g}} } \right]} \right\}, \\ & \quad \times \left\{ {1 + R_{\text{p}} \exp \left[ { - \left( {n_{1} (t) - \frac{{n_{3} (t)}}{2}} \right)\sigma_{\text{D2}} (\lambda )L_{\text{g}} } \right]} \right\}{\text{d}}\lambda \\ \end{aligned}$$
(6)

where η mode is the mode-matching efficiency, η del is the pump delivery efficiency from the LD pump source to the alkali medium, V L is the mode volume of the alkali laser that intercepts the gain medium, P p(λ) is the spectrally resolved pumping power with a Gaussian distribution profile, and R p is the reflectance of the pumping light at the rear mirror in the laser cavity. Because of the presence of the helium and methane buffer gases, the homogeneous collisional broadening of the D2 line is much greater than the inhomogeneous Doppler broadening. Therefore, we can express the spectrally resolved pump-absorption cross section σ D2(λ) as follows:

$$\sigma_{\text{D2}} (\lambda ) = \frac{{\sigma_{31} }}{{1 + \left( {\frac{{\left( {\lambda - \lambda_{\text{D2}} } \right)2c}}{{\Delta \nu_{\text{D2}} \lambda^{2} }}} \right)^{2} }},$$
(7)

where ∆ν D2 is the broadened pump-absorption linewidth (FWHM), σ 31 is the peak collisionally broadened cross section, and λ D2 is the center wavelength of the D2 line and varies with the partial pressure of the buffer gases in the cell. These parameters yield the following expressions [7]:

$$\begin{aligned}\Delta \nu_{\text{D2}} & = \varGamma_{\text{D2}}^{\text{He}} P_{\text{He}} \sqrt{\frac{T}{353}} + \varGamma_{\text{D2}}^{\text{methane}} P_{\text{methane}} \sqrt{\frac{T}{393}} \\ \sigma_{31} & = \frac{{\Delta \nu_{\text{D2}}^{\text{radiative}} }}{{\Delta \nu_{\text{D2}} }}\sigma_{\text{D2}}^{\text{radiative}} \\ \lambda_{\text{D2}} & = \lambda_{\text{D2}}^{\text{vacuum}} + \delta_{\text{He}} P_{\text{He}} + \delta_{\text{methane}} P_{\text{methane}} , \\ \end{aligned}$$
(8)

where P He and P methane are the partial pressures of helium and methane in the cell, respectively, and \(\varGamma_{\text{D2}}^{\text{He}}\) and \(\varGamma_{\text{D2}}^{\text{methane}}\) are the broadening coefficients of the D2 line related to helium and methane, respectively. Note that \(\varGamma_{\text{D2}}^{\text{He}}\) and \(\varGamma_{\text{D2}}^{\text{methane}}\) are measured at temperatures of 353 and 393 K, respectively [37, 38]. δ He and δ methane are the line-shifting coefficients of the D2 line for helium and methane, respectively. Δν radiativeD2 is the natural linewidth, σ radiativeD2 is the atomic cross section of rubidium, and λ vacuumD2 is the wavelength of the D2 line in vacuum.

Fig. 2
figure 2

a Output laser intensities in the time domain for various cell temperatures. b Waiting time as a function of the cell temperature. c Peak value of the laser intensity as a function of the cell temperature

Full size image

Additionally, the output laser intensity can be expressed as a function of the longitudinally averaged two-way laser intensity Ψ(t) as follows [39]:

$$I_{\text{laser}} = \psi (t)\frac{{\sigma_{21} (n_{2} (t) - n_{1} (t))l_{\text{g}} TT(1 - R_{\text{oc}} )\exp \left[ {\sigma_{21} (n_{2} (t) - n_{1} (t))l_{\text{g}} } \right]}}{{\left( {\exp \left[ {\sigma_{21} (n_{2} (t) - n_{1} (t))l_{\text{g}} } \right] - 1} \right)\left( {1 + TT^{2} R_{\text{oc}} \exp \left[ {\sigma_{21} (n_{2} (t) - n_{1} (t))l_{\text{g}} } \right]} \right)}}.$$
(9)

2.2 Spontaneous emission during generation in alkali lasers

Although spontaneous emission is usually neglected for a laser system with stable output, spontaneous emission must be considered in the calculation of ROs because it acts as a seed for stimulated emission at the onset of laser generation. Here, we introduce the physical expression for Ψ 1(t). The results are then used for the computation of ROs in a DPAL.

According to [40], the equation that governs the longitudinal number intensity of seed photons from spontaneous emission in a laser resonator is

$$\rho = \frac{{V_{\text{L}} }}{VS}n_{2} (t)\;c\sigma_{21} ,$$
(10)

where c is the velocity of light in vacuum, V is the mode volume in the cavity, and S is the area at the laser beam waist.

Thus, we can express Ψ 1(t) as follows:

$$\varPsi_{1} (t) = \rho \frac{{h\nu_{21} }}{{t_{\text{C}} }} = \frac{{V_{\text{L}} n_{2} (t)c\sigma_{21} \, h\nu_{21} }}{{VS\;t_{\text{C}} }},$$
(11)

where t c is the average lifetime of photons in the resonator, which can be expressed as

$$t_{\text{c}} = \frac{{2L_{\text{c}} }}{{c\left( {{\text{Loss}} + {\text{In}}(R_{\text{oc}} )} \right)}},$$
(12)

where L c is the cavity length and Loss is the resonator loss.

Assuming that the ratio of V L/V can be simplified to the ratio of L g/L c, we can obtain the following expression for Ψ 1(t) by combining Eq. (12) with Eq. (11):

$$\varPsi_{1} (t) = \frac{{L_{\text{g}} n_{2} (t)c^{2} \sigma_{21} \, h\nu_{21} \left[ {{\text{Loss}} + {\text{In}}\left( {R_{\text{oc}} } \right)} \right]}}{{2L_{\text{c}}^{2} S}}.$$
(13)

Equation (13) represents the contribution of spontaneous emission to the laser emission. This term is applied in the time-domain analyses at the onset of laser oscillation in the DPAL.

3 Results and discussions

By inserting the results for Γ P(t) and Ψ 1(t) in Eqs. (6) and (13) into Eq. (1), we become able to solve the differential equations by employing a Runge–Kutta approach. In the computation, we assume that all populations are located at the ground level and that the laser intensity in the vapor cell is zero prior to pumping irradiation. Thus, the initial conditions can be expressed as follows:

$$\begin{aligned} n_{1} (0) & = n_{0} \\ n_{2} (0) & = 0 \\ n_{3} (0) & = 0 \\ \varPsi (0) & = 0 \\ \end{aligned}$$
(14)

In this manner, the variations in the population distributions and the longitudinally averaged two-way laser intensity can be evaluated. We can therefore determine the time-domain features of the output laser intensity using Eq. (9). The results under various conditions are discussed in the following paragraphs.

3.1 Influence of the cell temperature

The alkali number density is primarily determined by the cell temperature. Therefore, the characteristics of the ROs should also be affected by the cell temperature. Figure 2a presents the results for the output laser density in the time domain for various cell temperatures. The values used in the calculation are as follows: a pumping power of 10 W with the beam waist of 420 μm; a linewidth of 50 GHz of a pumping LD which is a little wider than that of the rubidium vapor absorption; methane and helium pressures of 200 and 100 Torr, respectively; a cavity length L c of 8 cm; a medium length L g of 3 cm; and an output-coupler reflectance of 5 %.

In Fig. 2a, the RO phenomena can be easily observed in every curve. The time from the onset of pumping to the start of the first laser spike is defined as the “waiting time.” Utilizing the data presented in Fig. 2a, we can determine the relations between the cell temperature and the waiting time and between the cell temperature and the peak value of the laser intensity, as presented in Fig. 2b, c, respectively.

It is clear that the waiting time first decreases and then increases with increasing cell temperature. The reason for this behavior is that both the population density and the gain of the laser gaseous medium increase with the cell temperature. Such two parameters provide two opposite effects to the required time of achieving population inversion in a DPAL. Additionally, the peak laser intensity initially increases to its maximum value and then begins to decrease as the cell temperature continuously increases. This behavior can be understood as follows: When the cell temperature is low, the number density of alkali atoms is too small to achieve sufficient absorption of the pumping light, and the laser output remains relatively low. On the other hand, when the cell temperature becomes too high, the pump-photon absorption reaches saturation because of the rapidly increasing number density. In this case, it becomes difficult to maintain population inversion in a DPAL to produce a high peak laser intensity.

3.2 Influence of the methane pressure

In Fig. 3a, the output laser intensity is expressed as a function of the pumping time for various methane pressures. In the computation, the cell temperature is set to 400 K, and the other parameters are the same as in Subsect. 3.1. We can see that the RO becomes more evident at higher methane pressures.

Fig. 3
figure 3

a Output laser intensities in the time domain for various methane pressures. b Waiting time versus the methane pressure. c Peak value of the laser intensity versus the methane pressure

Full size image

Figure 3b, c illustrates the influence of the methane pressure on the waiting time and the peak value of the laser intensity, respectively. It is clear that the curve exhibits a local minimum in Fig. 3b and that the curve in Fig. 3c exhibits a local maximum. As the methane pressure increases, the fine-structure mixing rate increases and the cross sections (both the D1 and D2 lines) decrease. These two processes represent opposing tendencies, both of which can affect the waiting time and the output intensity. These competing effects lead to the presence of extrema in the characteristic curves presented in both Fig. 3b, c.

3.3 Influence of the pumping power

Figure 4a illustrates how the pumping power influences the output laser intensity in the time domain. At higher pumping powers, ROs are suppressed. The second spike is barely evident when the pumping power reaches 80 W. Note that the lasing threshold of the pumping power is about 4.95 W.

Fig. 4
figure 4

a Output laser intensities in the time domain at various pumping powers. b Dependence of the waiting time on the pumping power. c Dependence of the peak value of the laser intensity on the pumping power

Full size image

By referring to Eq. (6), it can be seen that the pump-photon absorption rate increases as the pumping power increases. Therefore, the waiting time decreases with increasing pumping power, and the peak laser intensity increases (see Fig. 4b, c). Note that there are no extrema in these curves, unlike those presented in Fig. 3b, c.

3.4 Influence of the cavity length

In Fig. 5a, the output laser intensity is presented as a function of the pumping time for various cavity lengths. From the figure, it is apparent that the RO phenomena become weak when the cavity length is relatively long. As the cavity length increases, the waiting time presents an ascending trend and the peak laser intensity exhibits the opposite tendency, as shown in Fig. 5b, c. This is primarily because the round-trip time for the laser cavity, which affects the time differential of the longitudinally averaged two-way laser intensity Ψ(t) [see the fifth formula in Eq. (1)], becomes longer with increasing cavity length. It is also apparent that the features of the ROs in a DPAL are insensitive to the cavity length.

Fig. 5
figure 5

a Output laser intensities in the time domain for various cavity lengths. b Variation of the waiting time with the cavity length. c Variation of the peak value of the laser intensity with the cavity length

Full size image

3.5 Influence of the reflectance of the output coupler

The output intensities in the time domain for various reflectances of the output coupler in a DPAL are presented in Fig. 6a. ROs become apparent as the reflectance of the output coupler decreases. As the reflectance increases, the waiting time decreases somewhat, as illustrated in Fig. 6b. However, changing the reflectance of the output coupler would not be an effective method of adjusting the waiting time. In Fig. 6c, the peak laser density is expressed as a function of the reflectance of the output coupler. It is evident from the figure that there is an optimal reflectance that yields the maximum value of the peak laser density. We can easily deduce that the gain of a DPAL should be much higher than those of conventional DPSSLs. This small optimal reflectance, which is simply a theoretical value based on kinetic analysis, may differ from that for a real DPAL because of the complexity of the dynamic processes inside the cell.

Fig. 6
figure 6

a Output laser intensities in the time domain for various reflectances of the output coupler. b Waiting time as a function of the reflectance of the output coupler. c Peak value of the laser intensity as a function of the reflectance of the output coupler

Full size image

The implications of this study can be summarized as follows:

  1. 1.

    To obtain strong ROs, a relatively high methane pressure, a relatively low pumping power, a relatively short cavity, and a relatively low reflectance of the output coupler are desirable.

  2. 2.

    To obtain a short waiting time, a relatively low cell temperature, an optimized methane pressure, a relatively high pumping power, a relatively short cavity, and a relatively high reflectance of the output coupler are desirable.

  3. 3.

    It can be seen that the amplitude of the first spike of RO even reaches 7.5 times (pump power of 80 W) as high as the steady state value. Such a spike may result in the damages of the optical elements of a high-powered DPAL. To obtain the weak peak intensity, an optimized cell temperature, a proper methane pressure, a relatively low pumping power, a relatively long cavity, and a relatively high reflectance of the output coupler are desirable.

3.6 Comparison of experimental and simulative results

In Ref. [21], the temporal waveforms were both theoretically evaluated and experimentally measured. By using the parameters given in Ref. [21], we simulate the laser pulse in time domain by assuming that the pump pulse has a Gaussian profile. The results are diagrammed in Fig. 7. It is obvious that the curve profile of the calculated result is near to that of the experimental one. In particular, the theoretical curve of our model is much closer to the experimental result than the simulation curve of Ref. [21]. The results prove that our theoretical system is reliable in analyses of the temporal characteristics of a DPAL.

Fig. 7
figure 7

Comparison of the experimental results in Fig. 10 of Ref. [21] (a) and the theoretical data based on our simulation (b)

Full size image

The RO phenomenon can also be observed in both simulated and experimental curves in Fig. 7. The waiting time in the simulation curve is almost the same as that in the experiment, but the intensity of the RO spike is somewhat higher than that of the experimental result. Such difference might be caused by the follow factors:

  1. 1.

    During the calculation, the temperature distribution in the cell is assumed to be homogeneous and the mode-match between the pump and the laser beams is supposed to be perfect. The assumptions would be somewhat different from the experimental conditions.

  2. 2.

    The sharp-edge of the RO spike will become dull because of the measurement error.

  3. 3.

    The difference between the assumed profile of a pump laser pulse and the real one will also affect the sharpness of the RO spike.

4 Conclusion

The lasing activity of a DPAL is, in fact, somewhat different from that of a normal three-level laser because of the unique relaxation process between its two upper levels. Thus, it is of fundamental interest to investigate the mechanism of the generation of ROs in a DPAL. In this paper, we establish a systematic kinetic model to analyze ROs in an end-pumped DPAL. We place particular focus on investigating the contribution of spontaneous emission to the laser emission of a DPAL in the time domain. The simulation results indicate that ROs, which have been observed and investigated in many types of lasers, should also manifest in a DPAL system. We analyze the characteristics of ROs under conditions of various cell temperatures, methane pressures, pump powers, cavity lengths, and output-coupler reflectances. The simulation results match well with the former published experimental data, and the reliability of our theoretical model has been therefore demonstrated. The results are believed to be valuable for the design of a stable high-powered DPAL.

Because the cell temperature and the alkali number density are presumed to be constant throughout the vapor cell in this study, some analytic deviations from the real case might be present in the computed results, especially when the pump intensity is strong. We are presently studying the temperature distribution inside the cell using a finite-difference (FD) approach. In addition, an experiment is under preparation to verify the theoretical consequences of the present study. We will present the improved model and the experimental results in the near future.