1 Introduction

During the past few years, there have been several reports on reconstructing three-dimensional (3D) tomographic structure based on compressive sensing (CS) theory using a single two-dimensional (2D) Gabor inline hologram. Because only a single hologram is needed, and the result suffers little from the out-of-focus features while still presenting relatively uniform background and little noise, holographic tomographic 3D imaging technology based on CS shows great potential applications. Brady et al. [1] were the first team that applied CS to visible light inline digital holography in 2009. In their work, the sizes of the hologram were 3.7 mm × 3.7 mm, and the maximum distance between the sample and the detector was 55 mm. The actual axial resolution was 8 mm. Subsequently, Cull et al. [2] conducted a research on millimeter–wave compressive holography. They reconstructed the 3D tomographic structure of several synthetic samples made of semitransparent polymer. The theoretical axial resolution was 20 mm while the actual resolution was 30 mm. Denis et al. [3] put forward a method of using sparsity constraints to reconstruct the 2D inline holograms in 2009. They conducted experiments at 532 nm and proposed that the method could be used for the 3D reconstruction. In 2011, Hahn et al. [4] realized 633 nm video–rate compressive holographic microscopic tomographic imaging. The actual spatial resolution was 5.2 μm, and the axial resolution was 60 μm. So far, imaging researches on compressive Gabor inline holographic tomography are all limited to domains of visible light and millimeter–wave without multiple obscurations.

The characteristic that Terahertz (THz) wave can penetrate nonmetallic and nonpolar materials has made THz imaging a research focus for more than 20 years. THz digital holography has great application prospects, such as in nondestructive inspection domain, because it can reduce the effect of diffraction and improve image resolution [5–11]. In this work, CW 2.52 THz compressive Gabor inline holographic tomographic imaging experiments have been conducted on several different targets including three copper letters on multiple Teflon boards, a paper clip and a handwritten character on a white paper. The single hologram obtained by multiple-frame averaging was utilized to reconstruct the 3D tomographic structure. To obtain better 3D image result, a modified reconstruction algorithm is proposed by coupling CS algorithm with negative transform, apodization and piecewise–nonlinear transformation function.

2 Algorithm principle

In digital holography, when conventional algorithms are used to reconstruct the 3D structure of a sample whose axial uniformity is unknown, or the phase delay of different planes is greater than 2π, a set of holograms must be recorded from different angles or using a series of wavelengths. Thus, the data volume is large which results in big computation. On the other hand, when the data volume of a single hologram is much smaller compared with the required data for reconstructing a 3D structure, the hologram can be regarded as a sparse data. Furthermore, the hologram is the linear recording of the sample diffraction field intensity, which satisfies the sparse conditions of CS [12, 13]. Therefore, CS can be used to reconstruct the 3D structure of the sample from a single hologram [1]. Assuming that the amplitude of the reference plane wave is 1, and the plane wave illuminates perpendicularly. The 3D scattering amplitude distribution of the sample is set as η(x 0, y 0, z 0), and the sample spacings along x and y axes in the hologram plane are Δ x  = Δ y  = Δ. The sampling pitch is Δ z along z axis. The number of pixels along each axis is N, and the number of 2D discrete reconstruction planes along z axis is N z . Based on Rayleigh–Sommerfeld diffraction integral function, the discrete model expression of the scattered field in the hologram plane is as follows [1]:

$$U_{H} (m_{H} ,n_{H} ) = \sum\limits_{{k_{0} = 1}}^{{N_{z} }} {\sum\limits_{{m_{0} = 1}}^{N} {\sum\limits_{{n_{0} = 1}}^{N} {\eta_{{k_{0} }} (m_{0} \Delta ,n_{0} \Delta ,k_{0} \Delta_{z} ) \times h_{{k_{0} }} } } } ((m_{H} - m_{0} )\Delta ,(n_{H} - n_{0} )\Delta ,k_{0} \Delta_{z} )$$
(1)

where \(\eta_{{k_{0} }}\)is the amplitude distribution of a certain 2D plane of η. h z is the systematic impulse response function.

The scattered field is known based on (1). Then, the recorded hologram I can be discretely expressed as [5]:

$$\begin{aligned} I &= |1 + U_{H} (m_{H} ,n_{H} )|^{2} \\ &= |1 + \sum\limits_{{k_{0} = 1}}^{{N_{z} }} {\sum\limits_{{m_{0} = 1}}^{N} {\sum\limits_{{n_{0} = 1}}^{N} {\eta_{{k_{0} }} (m_{0} \Delta ,n_{0} \Delta ,k_{0} \Delta_{z} ) \times h_{{k_{0} }} } } } ((m_{H} - m_{0} )\Delta ,(n_{H} - n_{0} )\Delta ,k_{0} \Delta_{z} )|^{2} \\ \end{aligned}$$
(2)

When the direct current (DC) term is eliminated and the nonlinearity of the autocorrelation term is neglected [1], there is a linear mapping between the diffraction field and I, which satisfies the linear measurement process. Then, I is expressed as [1]:

$$I = 2\text{Re} \left\{ {H\eta } \right\} + e$$
(3)

where H is the transformation matrix, e denotes the error effect of the DC and autocorrelation terms.

It can be inferred from the equations above that the relationship between U H and η can be expressed as follows [2]:

$$U_{H} = H\eta$$
(4)

The adjoint systematic model can be obtained by the inverse transform of (4) [14]:

$$\eta = H^{\prime }U_{H}$$
(5)

where the adjoint operator H′ is the Hermitian transpose matrix of H. This is just the backpropagation (BP) algorithm. Because the scattered field U H could not be obtained directly, the recorded hologram I is usually used for the reconstruction. Then, Eq. (5) represents that the 3D distribution could be acquired by inverse propagation operation of I. However, the reconstruction result is the 3D field distribution but not the 3D amplitude distribution of the sample. The undiffracted term and out-of-focus features will degrade the reconstruction result and make the range detection challenging and reduce the systematic resolution.

There is always a sharp contrast between the sample and background, thus the gradients of image edge and high-frequency noise positions are large and the others are close to zero. The reconstruction plane is sparse by calculating TV values [14]. The 3D reconstruction of the sample amplitude distribution can be made by solving the TV norm minimum based on CS. A sparsity restriction parameter is introduced to control the effect of TV values. Therefore, the answer to Eq. (3) is just the solution of minimizing the right terms of the following equation [1]:

$$\eta = \arg \mathop {\hbox{min} }\limits_{\eta \in R} (||I - H\eta ||_{2}^{2} + \tau ||\eta ||_{TV} )$$
(6)

where τ is the sparsity restriction parameter, and ||η|| TV is expressed as following [1]:

$$\left\| {\eta_{k} } \right\|_{TV} = \sum\limits_{k = 1}^{{N_{z} }} {\sum\limits_{m = 1}^{{N_{1} }} {\sum\limits_{n = 1}^{{N_{2} }} {\left| {\nabla (\eta_{k} (m,n))} \right|} } }$$
(7)

To solve Eq. (6), the two-step iterative shrinkage/thresholding algorithm (TwIST) is used in this paper which can be expressed as [15, 16]:

$$\eta_{1} = [\eta_{0} + {{H'(I - H\eta_{0} )} \mathord{\left/ {\vphantom {{H'(I - H\eta_{0} )} \nu }} \right. \kern-0pt} \nu }] - {{0.5\tau } \mathord{\left/ {\vphantom {{0.5\tau } \nu }} \right. \kern-0pt} \nu }\left\| {\eta_{0} + {{H'(I - H\eta_{0} )} \mathord{\left/ {\vphantom {{H'(I - H\eta_{0} )} \nu }} \right. \kern-0pt} \nu }} \right\|_{TV}$$
(8)
$$\eta_{t + 1} = (1 - \alpha )\eta_{t - 1} + (\alpha - \beta )\eta_{t} + \beta \{ [\eta_{t} + {{H'(I - H\eta_{t} )} \mathord{\left/ {\vphantom {{H'(I - H\eta_{t} )} \nu }} \right. \kern-0pt} \nu }] - {{0.5\tau } \mathord{\left/ {\vphantom {{0.5\tau } \nu }} \right. \kern-0pt} \nu }\left\| {\eta_{t} + {{H'(I - H\eta_{t} )} \mathord{\left/ {\vphantom {{H'(I - H\eta_{t} )} \nu }} \right. \kern-0pt} \nu }} \right\|_{TV} \}$$
(9)

where the parameters \(\alpha = {2 \mathord{\left/ {\vphantom {2 {(1 + \sqrt {1 - (\frac{1 - \kappa }{1 + \kappa })^{2} } )}}} \right. \kern-0pt} {(1 + \sqrt {1 - (\frac{1 - \kappa }{1 + \kappa })^{2} } )}}\), β = 2α/2α(λ 1 + λ N ).(λ 1 + λ N ) and κ = λ 1/λ 1 λ N .λ N . λ 1 and λ N represent the smallest and largest eigenvalues of the matrix H′H, respectively. To simplify the calculation complexity, we assume that λ 1 = 10−4, λ N  = 1. ν is the inverse scaling factor, which can ensure the iteration ongoing by controlling the values of τ and H′(I − Hη t ) terms. Iters is the total iteration number, t = 1, 2…, Iters. The initialization η 0 is set as a N 1 × N 2 × N z matrix whose elements are all one.

The number of nonzero elements is high in a Gabor inline hologram because the transparent area is always larger than the opaque area. By subtracting the hologram from the maximum value which is known as the negative transformation, the zero elements or close to zero elements are more than the nonzero elements. This operation leads to better satisfaction of CS theory. The negative transformation is also applied to the reconstructed result again. The holograms are all processed in this way when CS algorithm is used to reconstruct images.

To smooth the border data of the hologram and eliminate aperture diffraction effect, Tukey window function is used in this paper, which can be expressed as follows [17]:

$$w(m,n) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {0 \le |m| \le r\frac{M}{2},0 \le |n| \le r\frac{N}{2}} \hfill \\ {0.5\left\{ {1 + \cos \left[ {{{\pi \left( {m - r\frac{M}{2}} \right)} \mathord{\left/ {\vphantom {{\pi \left( {m - r\frac{M}{2}} \right)} {\left[ {2(1 - r)\frac{M}{2}} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {2(1 - r)\frac{M}{2}} \right]}}} \right]} \right\}} \hfill & {r\frac{M}{2} \le |m| \le \frac{M}{2},0 \le |n| \le r\frac{N}{2}} \hfill \\ {0.5\left\{ {1 + \cos \left[ {{{\pi \left( {n - r\frac{N}{2}} \right)} \mathord{\left/ {\vphantom {{\pi \left( {n - r\frac{N}{2}} \right)} {\left[ {2(1 - r)\frac{N}{2}} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {2(1 - r)\frac{N}{2}} \right]}}} \right]} \right\}} \hfill & {0 \le |m| \le r\frac{M}{2},r\frac{N}{2} \le |n| \le \frac{N}{2}} \hfill \\ \begin{gathered} 0.25\left\{ {1 + \cos \left[ {{{\pi \left( {m - r\frac{M}{2}} \right)} \mathord{\left/ {\vphantom {{\pi \left( {m - r\frac{M}{2}} \right)} {\left[ {2(1 - r)\frac{M}{2}} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {2(1 - r)\frac{M}{2}} \right]}}} \right]} \right\} \hfill \\ \quad \times \left\{ 1 + \cos \left[\pi \left(n - r\frac{N}{2}\right)/\left[2(1 - r)\frac{N}{2}\right]\right]\right\} \hfill \\ \end{gathered} \hfill & {r\frac{M}{2} \le |m| \le \frac{M}{2},r\frac{N}{2} \le |n| \le \frac{N}{2}{\text{ }}} \hfill \\ \end{array} } \right.$$
(10)

where r is the apodization parameter. M and N are the dimensions of the window.

To enhance image quality, the piecewise–nonlinear transformation function is used, which can be expressed as:

$$g(x,y) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {0 \le f(x,y) \le a} \hfill \\ {f(x,y)^{\gamma } } \hfill & {a < f(x,y) < b} \hfill \\ 1 \hfill & {b \le f(x,y) \le 1} \hfill \\ \end{array} } \right.$$
(11)

where γ is the transformation parameter. f represents the intensity value of the former image, and g is the result after transformation.

There is inevitably a displacement error between the reconstruction plane and the real position of the sample in the 3D reconstruction. The factors that might result in this error are explained as (1) the sample is not parallel to the photosurface; (2) the spacings between two adjacent samples are not equal; and (3) the real position could not be precisely measured. This error would affect the image quality of the reconstruction result. To reduce the displacement error effect, a modified reconstruction algorithm is proposed in this paper. The hologram after negative transformation is expanded to 208 × 208 by replicating the data on the boundary. The dimensions of the Tukey window are 208 × 208 whose apodization parameter is 0.4. Then, the expanded hologram is multiplied by the Tukey window to smooth the data on the boundary and is reconstructed with CS algorithm. The negative transformation is applied to the reconstructed images, and the result is cut into 124 × 124. The calculation flow diagram of the modified CS algorithm is shown in Fig. 1.

Fig. 1
figure 1

Flow diagram of the modified CS algorithm

Full size image

3 Numerical simulation analysis

Numerical simulation was firstly conducted. The holograms and reconstructed images are all normalized in this paper. To correlate with the real experiments, the dimensions of a pixel are set as 0.1 mm × 0.1 mm. The number of pixels of a hologram is 124 × 124, and the light wavelength is 118.83 μm. Three letters with different dimensions are used as the simulation samples, as shown in Fig. 2. The dimensions of the three letters are, respectively, 1.2 mm × 1.2 mm, 1.2 mm × 1.6 mm and 1.8 mm × 1.8 mm. And the line widths are 0.4, 0.4 and 0.6 mm, respectively.

Fig. 2
figure 2

Images of three simulation samples

Full size image

These three samples are placed 20, 28 and 36 mm away from the hologram plane firstly. The single hologram is shown in Fig. 3a. The number of iterations is 200, and the restriction parameter τ is 0.1 in this paper. The number of reconstruction planes is 20, and the spacing is 2 mm. The initial plane is set as z = 0. The reconstructed images with BP algorithm and CS algorithm are shown in Fig. 3b, c. Apparently, the reconstructed ‘T’, ‘H’ and ‘Z’ with CS algorithm are reconstructed well with clearly visible outline and little noise. However, in the reconstructed result with BP algorithm, the object features of the three characters are obscured by other out-of-focus planes, and there are reconstructed images of the samples in many reconstruction planes. The reconstruction quality is obviously worse than the CS reconstructed results.

Fig. 3
figure 3

Reconstruction results with backpropagation algorithm and CS algorithm when z = 16–38 mm: a hologram, b result with backpropagation, c result with CS

Full size image

The calculated mean and SD values for the reconstructed images when z = 18, 22, 24, 30, 32 and 38 mm and those for the letters when z = 20, 28 and 36 mm with two algorithms are shown in Table 1. The first six rows are the results of the whole images, and the last three rows are just the results of the reconstructed letters ‘T’, ‘H’ and ‘Z’. The mean values of the background with CS algorithm are close to 1, and the SD values are small. The gray values of the reconstructed characters are close to 0, and the SD values are also negligible. The gray values of the image with BP algorithm are about 0.67, and the characters also have relatively high gray values which show poor contrast and image quality. The reconstructed images and calculation results all indicate that the result with CS is free of undiffracted term and out-of-focus features to a great extent.

Table 1 Mean values and SD values of the images and letters with BP and CS algorithms
Full size table

Then, the displacement error is numerically simulated. Three samples are placed 19.5, 27.5 and 35.5 mm away from the hologram plane, respectively. The corresponding single hologram is shown in Fig. 4a. The parameters of CS algorithm are the same as above. The reconstruction results are shown in Fig. 4b, c, and the calculated mean and SD values are in Table 2. It can be observed that both of the reconstruction results suffered from degradation. Although the mean values of the reconstructed images and characters with BP algorithm increases and the SD values remain unchanged, the contrast declines and the outline of the character becomes blurry compared with Fig. 3a. The reconstructed images of the samples appear in many reconstruction planes and the mean and SD values of the characters all increase. The contrast and image quality drop. Based on the spatial resolution equations [1]: \(\Delta_{x} = \lambda \sqrt {1 + (2z/D)^{2} } /2\)and Δ z  = λ(2z/D)2, the theoretical lateral resolution is about 0.35 mm and axial resolution is about 2 mm. The reconstructed ‘T’ and ‘H’ in Fig. 4b can be distinguished, which illustrates that the lateral resolution is higher than 0.4 mm. When the reconstruction distance is z = 34–38 mm, the images have entire or partial ‘Z’. However, when z = 32 mm, any of reconstructed character can be hardly found from the reconstructed image. Therefore, it can be inferred that the axial resolution is higher than 3.5 mm.

Fig. 4
figure 4figure 4

Reconstruction results when there is a displacement error: a hologram, b result with backpropagation, c result with CS, d result with CS algorithm by expanding to 208 × 208 and apodization, e result after d image enhancement processing

Full size image
Table 2 Mean values and SD values of images and letters with BP and CS algorithms when there is a displacement error
Full size table

For the result shown in Fig. 4d, it is obviously that the distortion is less and the uniformity improves and the outline is sharper compared with the result shown in Fig. 4c. The result after image enhancement processing is shown in Fig. 4e, and the corresponding parameters a, b and γ are 0.4, 0.5 and 3, respectively. The calculated mean and SD values are in Table 3. It can be found that image enhancement processing can further improve the mean values of the image background. The mean values without reconstructed samples are 1, and the SD values are 0. The mean values of the ‘T’, ‘H’ and ‘Z’ after image enhancement processing are <0.1, indicating the improvement of the contrast. However, the SDs are slightly larger than before because the processing enlarges the gray value scale of the reconstructed samples by exponential transform.

Table 3 Mean values and SD of images and letters with BP and CS algorithms by expanding to 208 × 208 and apodization
Full size table

4 Experimental results and analysis

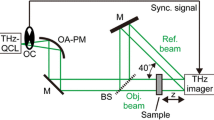
The CW 2.52 THz inline digital holographic imaging system in Ref. [5] is used. The THz source is a CO2 pumped continuous-wave laser. The pyroelectric camera Pyrocam III is used as the detector. The number of pixels of the detector is 124 × 124, and the pixel pitch is 100 μm. Two off-axis parabolic mirrors are used to compose a collimated lens combination. When the collimated wave illuminates the objects, the wave modulated by the objects information is used as object wave, and the rest transmitting wave is reference wave. The object wave and reference wave interfere in the detector surface to form a hologram.

Three letter samples are shown in Fig. 5. The distance between the adjacent two samples is about 8 mm, and the maximum distance between the detector plane and the sample is about 36 mm. Fig. 5a is the photograph of the three samples fixed on a 2D optical bracket. The board diagrams of the letters are shown in Fig. 5b. The minimum widths of the letters ‘T’, ‘H’ and ‘Z’ are 0.4, 0.4 and 0.6 mm, respectively. The corresponding dimensions are 1.2 × 1.2 mm2, 1.2 × 1.6 mm2 and 1.8 × 1.8 mm2, respectively. Although there is a circle of copper stripe around the sample, the Teflon board still has some deformation. Moreover, the density distribution is uneven. The distortion and unevenness result in additional imaging noise. The 40-frame averaged hologram is shown in Fig. 6. The black spots in the top-left corner and bottom-right corner are the bad spots of the detector. The number of iterations is 200, and the restriction parameter τ is 0.1. The number of reconstruction planes is 20, and the spacing is 2 mm. The initial reconstruction plane is set as z = 0. The reconstructed images with BP algorithm and CS algorithm are shown in Fig. 7a, b.

Fig. 5
figure 5

Photograph of three samples and board diagrams: a photograph of three samples, b letter board diagrams

Full size image
Fig. 6
figure 6

40-frame averaged hologram

Full size image
Fig. 7
figure 7figure 7

Reconstruction results of self-made cuprum letters ‘T’, ‘H’ and ‘Z’ when z = 16–38 mm: a backpropagation, b CS, c CS algorithm by expanding to 208 × 208 and apodization, d result after (c) image enhancement processing

Full size image

It can be found that the change trend of the reconstruction results with BP algorithm and CS algorithm is similar to the simulation result. The result with BP algorithm suffers from the out-of-focus features. The result with CS algorithm has better contrast and sharper outline than BP algorithm. However, as mentioned above, the reconstructed sample images exist in many planes and there is inconvenient noise in the result owing to the displacement error. The reconstructed ‘T’ and ‘H’ in Fig. 7b could be distinguished thus the actual lateral resolution is higher than 0.4 mm. When the reconstruction distance is z = 32–36 mm, the images have entire or partial ‘Z’. The reconstructed image when z = 38 mm almost shows no reconstructed character except a dot. Then, it can be inferred that the actual axial resolution is higher than 6 mm. By comparing the reconstructed images when z = 34 mm and z = 36 mm, we can infer that the actual optimal reconstruction distance of ‘Z’ might be between 35 and 36 mm. Likewise, the actual optimum reconstruction distance of ‘H’ might be between 27 and 28 mm. The reason for the relatively high gray values of ‘H’ and ‘Z’ is that the block of Teflon boards decreases the transmitting light intensity and degrades the contrast of the reconstructed images.

The 3D tomographic result with modified reconstruction algorithm is shown in Fig. 7c. The reconstructed images show much better outline and less noise. Though the transverse line of the reconstructed ‘Z’ has a distortion, the whole outline is clearer compared with Fig. 7b. The enhanced image is shown in Fig. 7d, and the corresponding parameters are 0.5, 0.9 and 3, respectively. The enlarged images when z = 20, 28 and 36 mm are shown in Fig. 8. It can be found that there is hardly any noise in the background and the intensity values of the letters are lower than those in Fig. 7b. However, the letter outline is still not clear and neat enough, which are mainly due to the deformation, blocking and nonuniform material distribution of the Teflon boards besides the non-optimal reconstruction distance.

Fig. 8
figure 8

Enlarged images when z = 20, 28 and 36 mm: a z = 20 mm, b z = 28 mm, c z = 36 mm

Full size image

The calculated mean values and SDs of the reconstructed images and letters before and after image enhancement processing are shown in Table 4. It can be easily found that the mean values of the image background after image enhancement processing are zero or close to zero and the SDs are basically less than those without image enhancement processing, which indicates that the denoising effect of background noise is desirable. The mean values of the ‘T’, ‘H’ and ‘Z’ after image enhancement processing become lower, which indicates that the contrast has been improved after image enhancement processing. Meanwhile, the SDs are still slightly larger than before.

Table 4 Mean values and SD of the reconstructed images and letters in different places before and after image enhancement
Full size table

Finally, a paper clip and a handwritten Chinese character ‘Dragon’ sample are also tested in this paper. The Chinese character is written on a white paper with a 2B graphite pencil. The photograph of the samples is shown in Fig. 9a, and the 100-frame averaged hologram is shown in Fig. 9b. The same procedure is applied to process the hologram. The number of iterations is 200, and the regularization parameter τ is 0.1. The number of reconstruction planes is 5, and the spacing is 5 mm. The initial reconstruction plane is set as z = 11 mm. The reconstruction result is shown in Fig. 9c. It can be found that the paper clip is well reconstructed. However, the reconstructed character ‘Dragon’ is incomplete and is hard to distinguish. The possible reasons contribute to this could be depicted as following. Firstly, the transmissivity of the white paper is much lower than Teflon boards. Secondly, the reflectivity of graphite is lower than metal copper and the uniformity of the white paper and handwritten character is not ideal. Lastly, the stroke dot in the top-right corner abuts against the paper clip and would be missing during iteration reconstruction.

Fig. 9
figure 9

Photograph of two handwritten letter samples, hologram and reconstruction result when z = 21 and 31 mm: a photograph of two samples, b 100-frame averaged hologram, c reconstruction result

Full size image

5 Conclusion

We have demonstrated the feasibility of 2.52 THz Gabor inline compressive holographic tomography to be applied for 3D tomographic reconstruction of samples blocked by multiple Teflon boards. A modified reconstruction algorithm is proposed by coupling CS algorithm with negative transform, apodization and piecewise–nonlinear transformation function. ‘T’, ‘H’ and ‘Z’ samples are placed in different positions along the optical axis and holograms are recorded. By numerically reconstructing, the 40-frame averaged hologram the 3D tomographic structure distribution can be well recovered. The axial resolution of the result can reach at least 6 mm while the lateral resolution stays higher than 0.4 mm. The numerical simulation and experimental results have verified the validity of reducing the noise effect caused by displacement error of the proposed modified CS algorithm. Meanwhile, the 3D tomographic images of the paper clip and handwritten character sample on the white paper are also obtained.