How bosonic is a pair of fermions?

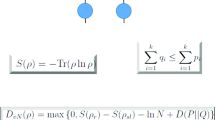
Abstract

Composite particles made of two fermions can be treated as ideal elementary bosons as long as the constituent fermions are sufficiently entangled. In that case, the Pauli principle acting on the parts does not jeopardise the bosonic behaviour of the whole. An indicator for bosonic quality is the composite boson normalisation ratio $\chi _{N+1}/\chi _{N}$ of a state of $N$ composites. This quantity is prohibitively complicated to compute exactly for realistic two-fermion wavefunctions and large composite numbers $N$. Here, we provide an efficient characterisation in terms of the purity $P$ and the largest eigenvalue $\lambda _1$ of the reduced single-fermion state. We find the states that extremise $\chi _N$ for given $P$ and $\lambda _1$, and we provide easily evaluable, saturable upper and lower bounds for the normalisation ratio. Our results strengthen the relationship between the bosonic quality of a composite particle and the entanglement of its constituents.

1 Introduction

At all physical scales, bosons and fermions emerge as the two fundamental species for identical particles, inseparably connected to their characteristic behaviour: The Pauli principle forbids two fermions to occupy the same state, while bosonic bunching favours such multiple occupation.

We routinely treat composite particles made of an even number of fermionic constituents as bosons, which seems justified a posteriori by the success of such description: From pions composed of two quarks [1] to molecules made of a large number of electrons and nuclei [2], bosonic behaviour is truly universal. At first sight, however, the Pauli principle that acts on the fermionic parts seems to jeopardise the bosonic behaviour of the whole. Notwithstanding this apparent obstacle, a microscopic theoretical treatment of two-fermion compounds explains the emergence of ideally behaving composite bosons: A compound of two fermions exhibits bosonic behaviour as long as the constituent fermions are sufficiently entangled [3–5], such that they effectively do not compete for single-fermion states and remain undisturbed by the Pauli principle [6, 7]. This observation connects our understanding of the almost perfect bosonic behaviour at all scales ranging from sub-nuclear physics [1] to ultracold molecules [2] with the tools and concepts of quantum information [4, 8, 9].

The composite boson normalisation ratio $\chi _{N+1}/\chi _N$ [3, 10–13] of states with $N+1$ and $N$ cobosons (composite bosons) captures the above argument quantitatively, as we discuss in more detail below. When it is close to unity, cobosons can be treated as elementary bosons [3], while deviations are observable in the statistical behaviour of the compounds [14–21]. The normalisation factor $\chi _{N}$ depends on the two-fermion wavefunction and answers our above question: “How bosonic is a pair of fermions?” Moreover, the argument can be taken to the realm of Cooper pairs [22] and composites made of two elementary bosons, for which a similar analysis is possible [3, 23].

The exact evaluation of $\chi _N$ becomes quickly unfeasible when the number of cobosons $N$ and the number of relevant single-fermion states $S$ are large, which makes approximations desirable. Simple saturable bounds to $\chi _N$ as a function of the purity $P$ of the single-fermion reduced state were derived in Refs. [12, 24], and an elegant algebraic approach to prove such bounds was put forward in [10]. For very small purities, $P \ll 1/N^2$, the upper and lower bounds converge, which yields an excellent characterisation of the emerging coboson. For moderate values of the purity $P \sim 1/N$, however, a considerable gap between the lower and the upper bound opens up [24]. In this regime, the $P$-dependent bounds do not characterise the coboson very well, and tighter bounds are desirable.

Here, we derive bounds for the normalisation factor $\chi _N$ and for the normalisation ratio $\chi _{N+1}/\chi _N$ for two-fermion cobosons which depend on the purity $P$ and on the largest eigenvalue $\lambda _1$ of the single-fermion density matrix ${\hat{\rho }}_{(a)}$, introduced below. The bounds can be evaluated efficiently for very large composite numbers $N$, and we show that they permit a significantly more precise characterisation of two-fermion cobosons than bounds in $P$ alone [12, 24].

We introduce the physics of cobosons and motivate the importance of the normalisation ratio in Sect. 2. Our main result, a set of saturable bounds for the normalisation ratio, is derived in Sect. 3. Examples and a discussion of the bounds are given in Sect. 4. An outlook on possible future developments that take into account further characteristics of the wavefunction is given in Sect. 5. Technical details regarding the derivation of the bounds are given in the Appendix 1 and 2.

2 Algebraic description of cobosons

2.1 Coboson normalisation factor

We consider two distinguishable¹ fermions of species $a$ and $b$ prepared in a collective wavefunction of the form

$$\begin{aligned} |\varPsi \rangle = \sum _{j,k=1}^{\infty } \omega _{j,k} |A_j, B_k\rangle , \end{aligned}$$

(1)

where we assume that the two-fermion state can be expanded on a discrete set of single-fermion states, which is fulfilled for bound states and also incorporates possible spin coupling. The bases $\{ |A_j\rangle \},\, \{ |B_k\rangle \}$ can be chosen at will, and it is convenient to use the Schmidt decomposition of $|\varPsi \rangle$ [25], i.e. to choose two particular single-particle bases $|a_j\rangle$ and $|b_j\rangle$ with

$$\begin{aligned}&|\varPsi \rangle = \sum _{j=1}^S \sqrt{\lambda _j} |a_j , b_j\rangle , \end{aligned}$$

(2)

$$\begin{aligned}&\lambda _1 \ge \lambda _2 \ge \ldots \ge 0,\quad \sum _{j=1}^S \lambda _j =1, \end{aligned}$$

(3)

where the ordering of the $S$ Schmidt coefficients $\lambda _j$ is imposed for convenience such that $\lambda _1$ be the largest coefficient in the distribution $\varvec{\Lambda }=(\lambda _1, \ldots , \lambda _S)$, and $S$ is not necessarily finite. The $\lambda _j$ coincide with the eigenvalues of either reduced single-fermion density matrix,

$$\begin{aligned} {\hat{\rho }}_{(a)}=\sum _{j=1}^S \lambda _j |a_j\rangle \langle a_j|, \quad {\hat{\rho }}_{(b)}=\sum _{j=1}^S \lambda _j |b_j\rangle \langle b_j| . \end{aligned}$$

(4)

We treat a pair of fermions in the state $|\Psi \rangle$ as a coboson, for which we can define an approximate creation operator in second quantisation [3]

$$\begin{aligned} {\hat{c}}^\dagger =\sum _{j=1}^S \sqrt{\lambda _j}\,{\hat{a}}^\dagger _j {\hat{b}}^\dagger _j =: \sum _{j=1}^S \sqrt{\lambda _j} \, {\hat{d}}^\dagger _j , \end{aligned}$$

(5)

where ${\hat{a}}^\dagger _j$ (${\hat{b}}^\dagger _j)$ creates a fermion in the Schmidt mode $|a_j\rangle$ $(|b_j\rangle )$. The operator ${\hat{d}}_j^\dagger$ creates a bi-fermion in a product state, i.e. a pair of two fermions in their respective mode $j$. While such creation and annihilation operators commute,

$$\begin{aligned} \left[ {\hat{d}}_j , {\hat{d}}_k \right]&= \left[ \hat{d}_j^\dagger , {\hat{d}}_k^\dagger \right] =0 , \end{aligned}$$

(6)

bi-fermions also obey the Pauli principle, such that

$$\begin{aligned} \left( {\hat{d}}_j^\dagger \right) ^2&= \left( {\hat{d}}_j \right) ^2 =0 . \end{aligned}$$

(7)

As a consequence, the operators ${\hat{c}}, {\hat{c}}^\dagger$ do not fulfil the ideal bosonic commutation relation, but obey [3]

$$\begin{aligned}{}[{\hat{c}}, {\hat{c}}^\dagger ] = 1 - \sum _{j=1}^S \lambda _j ( {\hat{a}}_j^\dagger {\hat{a}}_j + {\hat{b}}_j^\dagger {\hat{b}}_j ) . \end{aligned}$$

(8)

An $N$-coboson state is obtained by the $N$-fold application of the creation operator (5) on the vacuum [3],

$$\begin{aligned} |N\rangle =\frac{ \left( {\hat{c}}^\dagger \right) ^N }{ \sqrt{\chi ^{\varvec{\Lambda }}_N\, N!} }|0\rangle , \end{aligned}$$

(9)

where $\chi _N^{\varvec{\Lambda }} \le 1$ is the coboson normalisation factor [3, 11, 26], which ensures that $|N\rangle$ is normalised to unity. Inserting the definition of the coboson creation operator (5) into (9), we find

$$\begin{aligned} |N\rangle =\frac{1}{\sqrt{\chi _N^{\varvec{\Lambda }} N!}} \sum _{j_1 \ne j_2 \dots \ne j_N}^{1 \le j_m \le S} \prod _{k=1}^N \sqrt{\lambda _{j_k}} {\hat{d}}^\dagger _{j_k} , \end{aligned}$$

(10)

where terms with repeated indices $j_{m}=j_k$ do not contribute, due to the Pauli principle ensured by Eq. (7). In other words, the $N$-coboson state is a superposition of $N$ bi-fermions that are distributed among the bi-fermion Schmidt modes. Each distribution of the bi-fermions in the modes is weighted by $N!$ coherently superposed amplitudes.

2.2 Algebraic properties of the normalisation factor

By evaluating the norm of the $N$-coboson state in Eq. (10), one obtains a closed expression for the coboson normalisation factor $\chi _N^{\varvec{\Lambda }}$ as the elementary symmetric polynomial of degree $N$ in the Schmidt coefficients $\varvec{\Lambda }$ [27]:

$$\begin{aligned} \chi _N^{\varvec{\Lambda }}&= \varOmega \{ \underbrace{1 \ldots 1}_{N} \} , \end{aligned}$$

(11)

$$\begin{aligned} \varOmega \{ x_1 \dots x_N \}&= N! \sum _{1 \le p_1 < \ldots < p_N \le S} \prod _{k=1}^N \lambda _{p_k}^{x_k} , \end{aligned}$$

(12)

where the latter can be expressed recursively

$$\begin{aligned} \varOmega \{ x, \underbrace{1 \ldots 1}_{K} \} = M(x) { \varOmega }\{ \underbrace{ 1 \ldots 1 }_{K} \} - K{ \varOmega }\{ x+1, \underbrace{1\ldots 1 }_{K-1} \} , \end{aligned}$$

(13)

with the help of the power sums of order 1 to $N$,

$$\begin{aligned} M(k) = \sum _{j=1}^S \lambda _j^k,\quad M(2)\equiv P,\quad M(1)=1 . \end{aligned}$$

(14)

Alternatively, the Newton–Girard identities [13, 27] can be used,

$$\begin{aligned} \chi ^{\varvec{\Lambda }}_N=(N-1)! \sum _{m=1}^{N} \frac{(-1)^{1+m}\chi ^{\varvec{\Lambda }}_{N-m}}{(N-m)!} M(m) , \end{aligned}$$

(15)

which are more suitable in practice than Eqs. (12, 13).

The computation of $\chi _N$ becomes significantly simpler when all Schmidt coefficients in a distribution $\varvec{\Lambda }$ are identical. In this case, all summands in Eq. (12) are equal, and counting the number of terms gives

$$\begin{aligned} \chi _N^{\varvec{\Lambda }}&= \lambda ^{N} \frac{S!}{(S-N)!} \quad\text { for }\, \varvec{\Lambda }= (\underbrace{ \lambda \ldots \lambda }_{S}) , \end{aligned}$$

(16)

which can be combined with [23]

$$\begin{aligned} \chi _N^{(\lambda _1 \ldots \lambda _S ) } = \sum _{M=0}^N \chi _M^{( \lambda _1 \ldots \lambda _L )} \, \chi _{N-M}^{ ( \lambda _{L+1} \ldots \lambda _S )} { N \atopwithdelims ()M } , \end{aligned}$$

(17)

to quickly yield $\chi _N^{\varvec{\Lambda }}$ for distributions $\varvec{\Lambda }$ with large Schmidt coefficient multiplicities.

2.3 Bosonic behaviour in relation to the normalisation ratio

The normalisation ratio $\chi _{N+1}^{\varvec{\Lambda }}/\chi _N^{\varvec{\Lambda }}$ [3] determines the bosonic quality of a state of $N$ cobosons. For an intuitive picture, consider one summand in Eq. (10), in which the $N$ bi-fermions occupy the modes $j_1, \ldots , j_N$. In order to add an $N+1$st coboson to the state $|N\rangle$, we need to accommodate it among the $S-N$ unoccupied Schmidt modes. The probability that the added bi-fermion successfully ends up in an unoccupied Schmidt mode is then the sum of the coefficients associated with these unoccupied modes, $\sum _{m \notin \{ j_1, \ldots , j_N \} } \lambda _m$. This argument can be repeated for each configuration $j_1, \ldots , j_N$, and the success probability to add an $N+1$st coboson to an $N$-coboson state becomes

$$\begin{aligned} \frac{1}{\chi _N^{\varvec{\Lambda }}} \sum _{j_1 \ne j_2 \ldots \ne j_N}^{1 \le j_m \le S} \prod _{k=1}^N \lambda _{j_k} \left[ \sum _{m \notin \{ j_1, \ldots , j_N \} } \lambda _m \right] \nonumber \\ = \frac{1}{\chi _N^{\varvec{\Lambda }}} \sum _{j_1 \ne j_2 \ldots \ne j_N \ne j_{N+1}}^{1 \le j_m \le S} \prod _{k=1}^{N+1} \lambda _{j_k} = \frac{\chi _{N+1}^{\varvec{\Lambda }}}{\chi _N^{\varvec{\Lambda }}} , \end{aligned}$$

(18)

which is reflected by the sub-normalisation of the state obtained upon application of the creation operator ${\hat{c}}^\dagger$ on the $N$-coboson state [12]

$$\begin{aligned} {\hat{c}}^\dagger |N\rangle = \sqrt{\frac{\chi _{N+1}^{\varvec{\Lambda }}}{\chi _N^{\varvec{\Lambda }}}} \sqrt{N+1} |N+1\rangle . \end{aligned}$$

(19)

On the other hand, the annihilation of a coboson in an $N$-coboson state yields a state that contains a component orthogonal to the $(N-1)$-coboson state [3],

$$\begin{aligned} {\hat{c}} |N\rangle =\sqrt{ \frac{\chi _{N}^{\varvec{\Lambda }}}{\chi _{N-1}^{\varvec{\Lambda }}}}\sqrt{N} |N-1\rangle + |\epsilon _N\rangle , \end{aligned}$$

(20)

with

$$\begin{aligned} \langle {\epsilon _N}|{\epsilon _N}\rangle =1-N \frac{\chi _N^{\varvec{\Lambda }}}{\chi _{N-1}^{\varvec{\Lambda }}} + (N-1) \frac{\chi _{N+1}^{\varvec{\Lambda }}}{\chi _{N}^{\varvec{\Lambda }}} . \end{aligned}$$

(21)

Combining the relations (19) and (20), one finds the expectation value of the commutator (8) on an $N$-coboson state [3, 10, 13],

$$\begin{aligned} \langle N| \left[ {\hat{c}}, {\hat{c}}^\dagger \right] |N\rangle&= 1- 2\sum _{j=1}^S \lambda _j {\langle N|} {\hat{n}}_j |N\rangle \nonumber \\&= 2 \frac{\chi ^{\varvec{\Lambda }}_{N+1}}{\chi ^{\varvec{\Lambda }}_N} -1 , \end{aligned}$$

(22)

where ${\hat{n}}_j={\hat{d}}^\dagger _j {\hat{d}}_j$ counts the number of bi-fermions in mode $j$. For an ideal boson, Eq. (22) will equate to unity. Since all observable bosonic behaviour is borne by the bosonic commutation relations, values of $\chi _{N+1}^{\varvec{\Lambda }}/\chi _N^{\varvec{\Lambda }}$ close to unity witness a statistical behaviour that is close to the ideal bosonic one, while deviations from unity come with observable consequences that are induced by the statistics of the constituent fermions [15–17, 20, 28].

3 Bounds on the normalisation factor and ratio

Given a wavefunction $|\Psi \rangle$ of two distinguishable fermions, one can, in principle, diagonalise one reduced single-fermion density matrix ${\hat{\rho }}_{(a/b)}$ to obtain the distribution $\varvec{\Lambda }$ and compute $\chi _N$ with the help of the previous formulae, Eqs. (11, 12, 15, 16, 17).

In practice, however, even if the full distribution $\varvec{\Lambda }$ or all relevant power sums $M(2) \ldots M(N)$ are actually known, the evaluation of the normalisation factor $\chi _N$ is unfeasible for very large numbers of cobosons: Using Eq. (15), for example, the computation of $\chi _N$ requires the knowledge of all $\chi _M$ with $M<N$. Already for a harmonically trapped condensate of hydrogen atoms, the exact approach turns out to be unfeasible [12].

A characterisation of $\chi _N$ in terms of few, well-accessible quantities, such as the largest eigenvalue $\lambda _1$ and the purity $P$ of the reduced single-fermion density matrix is therefore essential in practice. The largest eigenvalue can be approximated via power iteration [25], while the purity is basis-independent and fulfils $P=\text {Tr}[{\hat{\rho }}_{(a)}^2]=\text {Tr}[{\hat{\rho }}_{(b)}^2]$. Full diagonalisation of ${\hat{\rho }}_{(a/b)}$ is not necessary for either quantity, while both bear clear physical meaning as quantifier of entanglement: The Schmidt number [4, 29] is defined as $K=1/P$, the geometric measure of entanglement [30] fulfils $E_G=1-\lambda_1$.

Upper and lower bounds to the normalisation factor $\chi _N^{\varvec{\Lambda }}$ and to the normalisation ratio $\chi _{N+1}^{\varvec{\Lambda }}/\chi _{N}^{\varvec{\Lambda }}$ in terms of $P$ and $\lambda _1$ are therefore highly desirable, not only to permit the efficient evaluation of $\chi _N$ in practice, but also to provide a better physical understanding of the connection between quantum entanglement and bosonic behaviour.

Bounds as a function of the single-fermion purity $P\equiv M(2)=\text {Tr}[\hat \rho_{(a/b)}^2]$ were put forward previously [10, 12, 13, 24]. In the regime $P \ll 1/N^2$, the bounds are efficient and tightly confine the possible values of $\chi _N$ and $\chi _{N+1}/\chi _N$ [24]. For moderate values of $P \sim 1/N$, however, the upper and lower bounds differ considerably, i.e. the compounds are not well characterised by $P$ alone, and higher-order power sums $M(m \ge 3)$ become important in the expansion in Eq. (15).

Here, we formulate bounds that depend on $P$ and on the largest Schmidt coefficient $\lambda _1$. Existing bounds [10, 12, 24] emerge naturally as extremal cases in the limit of the minimal and maximal value of $\lambda _1$ for a given $P$. The extremal distributions of Schmidt coefficients that emerge below coincide with the ones derived in Ref. [23] for two-boson composites. The alternating sign in Eq. (15), however, has no analogy for two-boson compounds, such that the approach of Ref. [23] needs to be adapted to fit the present case.

3.1 Lower bound in $P$ and $\lambda _1$

We assume that we are given a distribution $\varvec{\Lambda }$ with largest Schmidt coefficient $\lambda _1$ and purity $P$. The distribution $\varvec{\Lambda }_{\text {min}}(P, \lambda _1)$ that minimises $\chi _N$ under these constraints is derived in Appendix 1.

The resulting minimising distribution $\varvec{\Lambda }_{\text {min}}(P, \lambda _1)$ [23] contains $S$ non-vanishing Schmidt coefficients, with ${\lambda _1 \ge \lambda _2 = \lambda _3 = \dots = \lambda _{S-1} \ge \lambda _S}$, and

$$\begin{aligned} S=1 + \left\lceil \frac{(1-\lambda _1)^2}{P-\lambda _1^2} \right\rceil . \end{aligned}$$

(23)

The normalisation in Eq. (3) and the fixed purity $P$ imply for the Schmidt coefficients $\lambda _j$

$$\begin{aligned} \lambda _1 + (S-2) \lambda _2 + \lambda _S&= 1 , \nonumber \\ \lambda _1^2 + (S-2) \lambda _2^2 + \lambda _S^2&= P . \end{aligned}$$

(24)

With

$$\begin{aligned} R= \sqrt{(S - 2) ( \lambda _1 (2 - S \lambda _1) + (S - 1) P - 1)} , \end{aligned}$$

(25)

the relevant solution to Eq. (24) is [23]

$$\begin{aligned} \lambda _{2, \ldots , S-1}&= \frac{1-\lambda _1}{S-1} + \frac{R}{(S-2)(S-1)} , \nonumber \\ \lambda _S&= \frac{1-\lambda _1-R}{S-1} , \end{aligned}$$

(26)

where $\lambda _1 \ge \lambda _2 \ge \lambda _S$ is fulfilled by construction.

Given such distribution of three distinct Schmidt coefficients $\lambda _1, \lambda _2, \lambda _S$ with multiplicities $1, S-2, 1$, respectively, we can compute $\chi _N^{\varvec{\Lambda }_{\text {min}}(P, \lambda _1)}$ using Eqs. (16, 17):

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text {min}}(P,\lambda _1)} = \lambda _2^{N-2}\left[ (N - S) \lambda _2 ((N - S+1) \lambda _2 - N (\lambda _1 + \lambda _S) ) + (N-1 ) N \lambda _1 \lambda _S \right] \frac{(S-2)!}{(S-N)! } , \end{aligned}$$

(27)

where we used $1/k! = 0$ for $k<0$. Given $\lambda _1$ and $P$, this expression can be readily evaluated, even for large values of $N$.

Consistent with the Pauli principle, it is impossible to populate $S$ Schmidt modes with $N>S$ bi-fermions, which is ensured by the factor $1/(S-N)!$ in Eq. (27). In general, Eq. (23) imposes

$$\begin{aligned} 2 + \left\lceil \frac{(1-\lambda _1)^2}{(P-\lambda _1^2)} \right\rceil \le N \Rightarrow \chi _N^{\varvec{\Lambda }_{\text {min}}(\lambda _1, P) } = 0 . \end{aligned}$$

(28)

The normalisation ratio ${\chi _{N+1}^{\varvec{\Lambda }_{\text {min}}(P,\lambda _1)} }/ {\chi _{N}^{\varvec{\Lambda }_{\text {min}}(P,\lambda _1)}}$ is a monotonically increasing function of $S$. We can therefore obtain a simpler, however, slightly weaker, lower bound for Eq. (27) by setting $S=1+(1-\lambda _1)^2/(P-\lambda _1^2)$, i.e. we omit the ceiling function in Eq. (23):

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text {min}}(\lambda _1, P) } \ge \frac{ \varGamma \left[ \frac{ (1- \lambda _1)^2}{P - \lambda _1^2} \right] }{ \varGamma \left[ 2 - N + \frac{ (1- \lambda _1)^2}{P - \lambda _1^2} \right] }\times \left( 1 + \left( N-2 \right) \lambda _1- P \left( N-1\right) \right) \left( \frac{P - \lambda _1^2}{1 - \lambda _1} \right) ^{N-2} , \end{aligned}$$

(29)

which is only applicable for $1 + \left\lceil \frac{(1-\lambda _1)^2}{(P-\lambda _1^2)} \right\rceil \ge N$ [see Eq. (28)]. For values of $P$ and $\lambda _1$ for which $(1-\lambda _1)^2/(P-\lambda _1^2)$ is integer, the smooth lower bound Eq. (29) exactly coincides with the exact expression, Eq. (27).

3.2 Upper bound in $P$ and $\lambda _1$

In strict analogy to the last section, we construct the distribution $\varvec{\Lambda }_{\text {max}}(\lambda _1, P)$ that maximises the normalisation constant $\chi _N$ for fixed $\lambda _1$ and $P$ in Appendix 2.

In $\varvec{\Lambda }_{\text {max}}(\lambda _1, P)$ [23], the multiplicity of $\lambda _1$ is chosen as large as possible, i.e. $\lambda _1$ is repeated $L-1$ times, with $L=\lceil P/\lambda _1^2 \rceil$. The $L$th coefficient is then maximised, while the remaining $S-L$ coefficients fulfil ${\lambda _1=\lambda _2=\ldots = \lambda _{L-1} \ge \lambda _L \ge \lambda _{L+1} = \dots = \lambda _S }$. To ensure normalisation [Eq. (3)] and satisfy $M(2)=P$, we have

$$\begin{aligned} (L-1) \lambda _1 + \lambda _L + (S-L) \lambda _S&= 1 , \nonumber \\ (L-1) \lambda _1^2 + \lambda _L^2 + (S-L) \lambda _S^2&= P . \end{aligned}$$

(30)

With

$$\begin{aligned} R^\prime =\sqrt{( S-L) ( P (S+1- L)-1 + ( L-1) \lambda _1 (2 - \lambda _1 S))} , \end{aligned}$$

we find the relevant solution for $\lambda _L$ and $\lambda _S$ [23],

$$\begin{aligned} \lambda _L&= \frac{ 1-(L-1)\lambda _1+R^\prime }{S+1-L} , \nonumber \\ \lambda _{S}&= \frac{1-(L-1)\lambda _1}{S+1-L} -\frac{R^\prime }{(S-L)(S+1-L)} , \end{aligned}$$

(31)

where, in order to ensure $\lambda _S, \lambda _L \ge 0,\, S$ needs to fulfill

$$\begin{aligned} S > \frac{(L-1)P+1-2(L-1)\lambda _1}{P-(L-1)\lambda _1^2}. \end{aligned}$$

(32)

Using Eqs. (17, 16), the normalisation factor for the maximising distribution becomes

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text {max}}(P, \lambda _1)}&\mathop {=}\limits ^{\text {Eq.(17)}} \sum _{K=0}^N \sum _{M=0}^{N-K} \chi ^{(\lambda _1, \ldots , \lambda _1)}_{M} \chi ^{(\lambda _L)}_{K} \chi ^{(\lambda _S, \ldots , \lambda _S)}_{N-M-K} {N \atopwithdelims ()M, K} \nonumber \\&\mathop {=}\limits ^{\text {Eq.(16)}} \sum _{K=0}^1 \sum _{M=0}^{N-K} \frac{(L-1)!}{(L-1-M)!} \frac{(S-L)!}{(S-L-(N-K-M))!} \lambda _1^{M} \lambda _L^K \lambda _S^{N-M-K} {N \atopwithdelims ()M, K} , \end{aligned}$$

(33)

where ${ X \atopwithdelims ()Y, Z}=\frac{X!}{Y! Z! (X-Y-Z)!}$ is the multinomial coefficient. Since this expression is an increasing function of $S$, we maximise it in the limit $S \rightarrow \infty$. Defining $\lambda _\Sigma$ as the sum of all infinitesimal coefficients $\lambda _S$ in that limit, we find

$$\begin{aligned} \lambda _\Sigma\, = \, 1-(L-1)\lambda _1-\sqrt{\lambda _1^2(1-L)+P}, \qquad \lim _{S\rightarrow \infty } \chi ^{(\lambda _S, \ldots , \lambda _S)}_{N-M-K}= \lambda _\Sigma ^{N-M-K} , \end{aligned}$$

(34)

which gives

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text {max}}(P, \lambda _1)}&= \sum _{K=0}^1 \sum _{M=0}^{N-K} \frac{(L-1)!}{(L-1-M)!} \lambda _1^{M} \lambda _L^K \lambda _\Sigma ^{N-M-K} {N \atopwithdelims ()M, K} \nonumber \\&= (-\lambda _1)^{L-1}\lambda _\Sigma ^{N-L} \left[ N \lambda _L \,\mathcal {U}\left( 1-L,1-L+N,-\frac{\lambda _\Sigma }{\lambda _1}\right) + \lambda _\Sigma \,\mathcal {U}\left( 1-L,2-L+N,-\frac{\lambda _\Sigma }{\lambda _1}\right) \right] , \end{aligned}$$

(35)

where $\mathcal {U}(a,b,z)$ is Tricomi’s confluent hypergeometric function [31], which allows fast numerical evaluation in practice. Using $\lambda _1 \ge \lambda _L$, we find a simpler upper bound to the above expression:

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text {max}}(P, \lambda _1)} \le \sum _{M=0}^{\min (N,\lfloor {\tilde{L}} \rfloor +1 )} \frac{ \varGamma \left( {\tilde{L}}+1 \right) }{\varGamma \left( {\tilde{L}}-M+1 \right) } \lambda _1^{M} \lambda _\Sigma ^{N-M} {N \atopwithdelims ()M} , \end{aligned}$$

(36)

where ${\tilde{L}}=P/\lambda _1^2$ (note the omitted ceiling function), ${\lambda}_{\Sigma}$ is evaluated for $L=\tilde L$. The last expression coincides with Eq. (35) when $P/\lambda _1^2$ is integer, since in that case $L={\tilde{L}}$ and $\lambda _L=\lambda _1$.

We compare the tight saturable bounds, Eqs. (27) and (35), with their respective smooth approximations, Eqs. (29) and (36), in Fig. 1.

Fig. 1

Exact values of the normalisation ratio $\chi _{N+1}/\chi _N$ for the minimising and maximising distribution [black solid lines, computed using Eqs. (27, 35)] and smooth upper and lower bounds [blue dashed lines, Eqs. (29, 36)]. Upper row $N=4$, lower row $N=10$. Left column Fixed purity $P$, the normalisation ratio is shown as a function of the largest Schmidt coefficient $\lambda _1$. Right column Fixed $\lambda _1$, the normalisation ratio is shown as a function of $P$. The normalisation ratio of any distribution $\varvec{\Lambda }$ with $P$ and $\lambda _1$ is restricted to the shaded range delimited by the black solid line

3.3 Bounds in $P$

The parameters $\lambda _1$ and $P$ cannot be chosen independently, since, by construction [23],

$$\begin{aligned} P \le \lambda _{1,\text {min}}(P)&\le \lambda _1 \le \lambda _{1,\text {max}}(P) = \sqrt{P} , \end{aligned}$$

(37)

where

$$\begin{aligned} \lambda _{1,\text {min}}(P)&= \frac{1}{\left\lceil \frac{1}{P} \right\rceil } \left( \sqrt{\frac{P \left\lceil \frac{1}{P} \right\rceil -1}{{\left\lceil \frac{1}{P} \right\rceil -1}}}+1 \right) . \end{aligned}$$

(38)

We obtain $P$-dependent and $\lambda _1$-independent upper (lower) bounds to $\chi _N$ and $\chi _{N+1}/\chi _N$ by fixing $P$ and setting the largest Schmidt coefficient to its extremal value, $\lambda _{1,\text {max(min)}}(P)$.

3.3.1 Upper bound in $P$

We maximise the normalisation factor and ratio by choosing $\lambda _{1}=\lambda _{1,\text {max}}(P)=\sqrt{P}$. The minimising distribution $\varvec{\Lambda }_{\text {min}}(P,\lambda _1)$ and the maximising distribution $\varvec{\Lambda }_{\text {max}}(P,\lambda _1)$ then both converge to the peaked distribution [24], $\vec {\varvec {\Lambda}}_{\text{peak}}(P)$, given by the limit $S\rightarrow \infty$ of

$$\begin{aligned} \lambda _{1,\text {peak}}&= \frac{1 + \sqrt{(S-1)(S P -1)}}{S}, \nonumber \\ \lambda _{j \in \{ 2\dots S\},\text {peak}}&= \frac{1-\lambda _{1,\text {peak}}}{S-1} . \end{aligned}$$

(39)

Via Eqs. (16, 17), we recover the $P$-dependent upper bound [24]

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text peak}(P)} = (1-\sqrt{P})^{N-1} \left[ 1+(N-1) \sqrt{P} \right] . \end{aligned}$$

(40)

3.3.2 Lower bound in $P$

The normalisation factor and ratio are minimised for fixed $P$ by choosing ${\lambda _{1}=\lambda _{1,\text {min}}(P)}$, as given by Eq. (38). In this case, both distributions $\varvec{\Lambda }_{\text {min}}(P,\lambda _1)$ and $\varvec{\Lambda }_{\text {max}}(P,\lambda _1)$ become the uniform distribution [15], $\varvec{\Lambda }_{\text uni}(P)$, with $S=L=\left\lceil \frac{1}{P} \right\rceil$ non-vanishing Schmidt coefficients given by

$$\begin{aligned} \lambda _{j \in \{ 1\ldots L-1\},\text {uni}}&= \lambda _{1,\text {min}}(P) , \nonumber \\ \lambda _{L,\text {uni}}&= 1-\lambda _{1,\text {min}}(P) (L-1) . \end{aligned}$$

(41)

Using Eqs. (16, 17), we recover the lower bound [24]

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text uni}(P)} = \frac{\lambda _{1,\text {uni}}^{N-1} (L-1)! }{(L-N)! } \left[ N-L\, \lambda _{1,\text {uni}}(N-1) \right] . \end{aligned}$$

(42)

3.4 Bounds in $\lambda _1$

The constraints on $\lambda _1$ and $P$ in Eq. (37) can be re-formulated as constraints on $P$:

$$\begin{aligned} \lambda _1^2 = P_{\text {min}}(\lambda _1)&\le P \le P_{\text {max}}(\lambda _1) \le \lambda _1, \end{aligned}$$

(43)

where

$$\begin{aligned} P_{\text {max}}(\lambda _1)&= \lambda _1^2 \left\lfloor \frac{1}{\lambda _1} \right\rfloor + \left( 1- \lambda _1 \left\lfloor \frac{1}{\lambda _1} \right\rfloor \right) ^2 . \end{aligned}$$

(44)

We obtain $\lambda _1$-dependent and $P$-independent upper (lower) bounds to the normalisation ratio and factor by choosing $P_{\text {min(max)}}(\lambda _1)$.

3.4.1 Upper bound in $\lambda _1$

For $P= P_{\text {min}}(\lambda _1)$, the distributions $\varvec{\Lambda }_{\text {min/max}}(P,\lambda _1)$ become a peaked distribution, $\varvec{\Lambda }_{\text {peak}}(P_{\text {min}}(\lambda _1))$, with the first Schmidt coefficient $\lambda _1$ and ($S-1$) coefficients of magnitude $(1-\lambda _1)/(S-1)$. In the limit $S\rightarrow \infty$ the normalisation factor reads

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text peak}(P_{\text {min}}(\lambda _1))} = (1-\lambda _1)^{N-1} (1+(N-1) \lambda _1) . \end{aligned}$$

(45)

Since $\lambda _1 \le \sqrt{P}$, this upper bound is always larger (i.e. weaker) than the upper bound in $P$ given by Eq. (40):

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text peak}(P_{\text {min}}(\lambda _1))} \ge \chi _N^{\varvec{\Lambda }_{\text peak}(P)} , \end{aligned}$$

(46)

for any pair $(P, \lambda _1)$ fulfilling Eq. (37).

Fig. 2

Hierarchy of minimising and maximising distributions. The circle diameters correspond to the magnitude of a Schmidt coefficient $\lambda _j$, and the fraction of filled area in each large circle is the purity $P$ of the respective distribution. A distribution $\varvec{\Lambda }$, with $\lambda _1=0.3$ and $P=0.2$ (centre) leads to a normalisation factor $\chi _N$ that is bound from below and from above by the $\chi _N$ evaluated for the distributions on the left and on the right, respectively. The order of the distributions reflects the hierarchy of Eq. (49). All circles that correspond to $\lambda _1$ are filled with dark red and marked with white arrows. The resulting normalisation ratios $\chi _{N+1}/\chi _N$ obey the same hierarchy, as illustrated by the intersections of the vertical lines $(i)$ with the three minimising and the three maximising limits in Fig. 3. The normalisation ratio of $\varvec{\Lambda }$ then lies on $(i)$ within the shaded area

3.4.2 Lower bound in $\lambda _1$

We find a lower bound in $\lambda _1$ by setting $P = P_{\text {max}}(\lambda _1)$, as given by Eq. (44). The resulting distribution contains the largest possible multiplicity of $\lambda _1$, i.e. it contains $L-1=S-1=\left\lfloor \frac{1}{\lambda _1}\right\rfloor$ coefficients of magnitude $\lambda _1$ and one of the magnitude $\left( 1-\left\lfloor \frac{1}{\lambda _1}\right\rfloor \lambda _1 \right)$. The resulting normalisation factor fulfils

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text uni}(P_{\text {max}}(\lambda _1))} = \frac{\lambda _1^{N-1} (L-1)! }{\left( L-N \right) ! }\left[ N- \lambda _1 L (N-1) \right] . \end{aligned}$$

(47)

In analogy to Eq. (46), this lower bound in $\lambda _1$ is always smaller (i.e. weaker) than the corresponding bound in $P$:

$$\begin{aligned} \chi _N^{\varvec{\Lambda }_{\text uni}(P_{\text {max}}(\lambda _1))} \le \chi _N^{\varvec{\Lambda }_{\text uni}(P)} , \end{aligned}$$

(48)

due to $P \le P_{\text {max}}$.

4 Summaries of the bounds and discussion

Examples for all pertinent distributions are shown in Fig. 2: A randomly chosen distribution $\varvec{\Lambda }$ (middle panel) with specified $\lambda _1$ and $P$ leads to a certain normalisation factor $\chi _N^{\varvec{\Lambda }}$, which is bound from below by the distributions on the left and from above by those from the right, successively. Summarising the attained values for the normalisation factor given in Eqs. (27, 35, 40, 42, 45, 47), we obtain our main result,

$$\begin{aligned}&\chi _N^{\varvec{\Lambda }_{\text {uni}}(P_{\text {max}}(\lambda _{1}))} \le \chi _N^{\varvec{\Lambda }_{\text {uni}}(P)} \le \chi _N^{\varvec{\Lambda }_{\text {min}}(\lambda _1, P) } \le \chi _N^{\varvec{\Lambda }} \nonumber \\&\quad \le \chi _N^{\varvec{\Lambda }_{\text {max}}(\lambda _1, P) }\le \chi _N^{\varvec{\Lambda }_{\text {peak}}(P)} \le \chi _N^{\varvec{\Lambda }_{\text {peak}}(P_{\text {min}}(\lambda _1) ) }. \end{aligned}$$

(49)

This hierarchy of consecutively tighter bounds is immediately inherited by the normalisation ratio $\chi _{N+1}/\chi _N$ in full analogy, which quantitatively answers our initial question, “How bosonic is a pair of fermions?”, in terms of $P$ and $\lambda _1$.

In order to obtain a physical understanding of these bounds, a combinatorial approach is instructive: The normalisation factor $\chi _N$ can be interpreted as the probability that a collection of $N$ objects that are each given a property $j$ with probability $\lambda _j$ does not contain any set of two or more objects with the same property [24] (for $S=365$ and $\lambda _j=1/365$, we recover the “birthday problem” [32]). In our physical context, no two or more bi-fermions are allowed to occupy the same Schmidt mode. The Pauli principle, enforced by Eq. (7), implies that the emerging $N$-coboson state in Eq. (10) does not contain any such terms describing multiple occupation. The lack of these terms then needs to be accounted for by the normalisation factor $\chi _N$.

4.1 Entanglement and bosonic behaviour

Fig. 3

Upper and lower bounds to the normalisation ratio $\chi _{N+1}/\chi _N$ as a function of $\lambda _1$ (left panels) and $P$ (right panels), for $N=3$ (top row) and $N=30$ (bottom row). Red dashed lines correspond to bounds in $\lambda _1$ alone, Eqs. (45, 47); blue dotted lines show the bounds in $P$ alone, Eq. (40, 42). The combined bounds, Eqs. (27, 35), are shown as solid black lines, the shaded area is the range allowed for general distributions $\varvec{\Lambda }$ with given $\lambda _1$ and $P$. The bounds in $P$ are always superior to those in $\lambda _1$. By setting $P$ (left panel) or $\lambda _1$ (right panel), the possible values of $\lambda _1$ and $P$, respectively, are constrained by Eqs. (37) and (43). The solid vertical lines in the upper panels indicate those values for which the maximising and minimising distributions are depicted in Fig. 2 [solid red lines (i), $\lambda _1=0.3, P=0.2$] and Fig. 4 [solid dark blue lines, $P=0.2$, (a) $\lambda _1=0.215$, (b) $\lambda _1=0.42$]. The vertical lines (ii) in the lower panel indicate corresponding values of $P$ and $\lambda _1$

Combinatorially speaking, the purity $P$ represents the probability that two randomly chosen objects possess the same property (it is therefore also called the collision entropy). Here, it reflects the probability that the wavefunction vanishes upon two bi-fermions competing for the same Schmidt mode. Therefore, the $P$-dependent bounds on $\chi _N$ decrease monotonically with increasing $P$ (blue dotted lines in the right panels of Fig. 3). Larger entanglement, characterised by a smaller purity $P$, is therefore tantamount to a more bosonic composite [3, 12, 24].

Similarly, the $\lambda _1$-dependent bounds decrease with increasing $\lambda _1$ (red dashed lines in the left panels of Fig. 3). Consistently, an increase in $\lambda _1$ also leads to weaker geometric entanglement, $E_G=1-\lambda _1$. This connection underlines, again, the relationship between quantum entanglement and the bosonic behaviour of composites.

The knowledge of $\lambda _1$ alone leaves a finite range for possible values of $P$ [see Eq. (43)]: The remaining, unknown Schmidt coefficients $\lambda _2\dots \lambda _S$ may be many and small, or few and large (compare the distribution $\varvec{\Lambda }_{\text {uni}}(P_{\text {max}}(\lambda _1))$ to $\varvec{\Lambda }_{\text {peak}}(P_{\text {min}}(\lambda _1))$ in Fig. 2). Indeed, the main sources of deviation from bosonic behaviour are binary "collisions” of bi-fermions, which is directly quantified by $P$. Therefore, bounds in $\lambda _1$ are always weaker than bounds in $P$; in the formalism of quantum information, the purity $P$ is more decisive than the overlap with the closest separable state, $\lambda _1$.

The knowledge of both, $\lambda _1$ and $P$, yields a considerable enhancement over bounds in $P$ alone (black solid lines in Fig. 3). In particular, the range of possible $\chi _N$ becomes narrower for extremal values of $P$ or $\lambda _1$, for which the minimising and maximising distributions resemble each other, as in Fig. 4. In this case, $\lambda _1$ and $P$ strongly constrain the remaining Schmidt coefficients.

In view of the clear dependence of $\chi _N$ on $P$ and $\lambda _1$, it is remarkable that the combined bound in $P$ and $\lambda _1$ features an increase in the bosonic quality $\chi _N$ and $\chi _{N+1}/\chi _N$ with $\lambda _1$ (Fig. 3). This increase, however, is due to the fixed purity $P$: By increasing the largest Schmidt coefficient $\lambda _1$, all other Schmidt coefficients need to decrease in order to keep $P$ constant, which naturally increases the total accessible number of Schmidt modes, and, consequently, $\chi _N$. More formally speaking, $\chi _N$ actually increases with $M(3)$, as can be inferred from Eqs. (13, 15) [13].

Fig. 4

Minimising and maximising distributions $\varvec{\Lambda }_\text{min/max }$, for close-to-extremal values of $\lambda _1$ and fixed $P=0.2$. (a) $\lambda _1=0.215 \gtrapprox \lambda _{1,\text {min}}(P)$. (b) $\lambda _1=0.42 \lessapprox \lambda _{1,\text {max}}(P)$. The emerging bounds correspond to the black solid lines in Fig. 3 at the intersections with arrows (a) and (b), respectively. For $\lambda _1 \rightarrow \lambda _{1,\mathrm max(min) }(P)$, the distributions converge to the peaked (uniform) distribution (compare to the corresponding sketches in Fig. 2)

Fig. 5

Upper and lower bounds to $(1-\chi _{N+1}/\chi _N)$, i.e. to the deviation from ideal bosonic behaviour, as a function of $N$. The colour code is the same as in Fig. 3. In all panels, $P=0.001$, i.e. the bounds in $P$ alone (blue dotted) do not change. We choose different values of $\lambda _1$: ${\textit\bf{(a)} } {\lambda _1=0.9 \lambda _{1,\text {min}} (P) + 0.1 \lambda _{1,\text {max}}(P) \approx 0.0041}$. ${\textit\bf{(b)} } {\lambda _1=0.5 \lambda _{1,\text {min}}(P) + 0.5 \lambda _{1,\text {max}}(P) \approx 0.0163}$. ${\textit\bf{(c)} } {\lambda _1=0.1 \lambda _{1,\text {min}} (P) + 0.9 \lambda _{1,\text {max}} (P) \approx 0.0286}$. ${\textit\bf{(d)} } {\lambda _1=0.01 \lambda _{1,\text {min}} (P) + 0.99 \lambda _{1,\text {max}} (P) \approx 0.0313}$

4.2 Limit of large coboson numbers $N$

In Fig. 5, we show the deviation from the ideal value $\chi _{N+1}/\chi _N=1$ as a function of the number of cobosons $N$. While the upper and lower bounds in $P$ converge for small values of $N < 1/\sqrt{P}$, bounds in $\lambda _1$ do not: For small particle numbers, the coboson behaviour is essentially defined by the binary collision probability, i.e. by the purity $P$. The magnitude of the largest Schmidt coefficient $\lambda _1$ is secondary. For large particle numbers $N > 1/\sqrt{P}$, the knowledge of $\lambda _1$ then fixes the possible range of $M(3)$, which constrains the accessible values of the normalisation ratio. Again, very large or very small values of $\lambda _1$ lead to a tighter confinement of the range of possible $\chi _{N+1}/\chi _N$ than intermediate values of $\lambda _1$, as can be seen by comparing the panels in Fig. 5. In general, $\lambda _1$ and $P$ determine to a wide extent up to which number of cobosons $N$ a condensate of two-fermion composites still behaves bosonically [6, 33].

In comparison to the bounds on the normalisation factor for cobosons made of two elementary bosons [23], the role of the $\lambda _1$-dependent bounds is exchanged: for two-fermion cobosons, $\chi _N$ is maximised (minimised) by choosing the smallest (largest) possible purity for a given $\lambda _1$; for two-boson cobosons, the normalisation factor instead increases with the purity. As a consequence, the clear hierarchy of bounds expressed by Eq. (49) is absent for two-boson cobosons [23]. This dependence is due to the possibility for multiple occupation of Schmidt modes by bosonic constituents, forbidden by the Pauli principle for fermionic constituents. Furthermore, when the number of cobosons $N$ is large, $N> 1/\lambda _1$, the behaviour of two-boson bosons is very well defined by $\lambda _1$ alone, and the multiple occupation of the most prominent Schmidt mode dominates the picture, a process without analogy in the present two-fermion case.

5 Conclusions and outlook

Starting with the general description of a two-fermion composite in Eqs. (2, 5), we confined the quantitative indicator $\chi _{N+1}/\chi _N$ for the bosonic behaviour of the resulting coboson. For a fixed purity $P$, the immediate difference between the state that minimises and the state that maximises $\chi _N$ is the magnitude of the largest Schmidt coefficient, which is of the order of $P$ for the minimal, uniform distribution, and $\sqrt{P}$ for the maximal, peaked distribution [24]. Therefore, the additional constraint on $\lambda _1$ can considerably enhance $P$-dependent bounds [10, 12, 24].

Our bounds strengthen the relation between quantum entanglement and the bosonic quality of bi-fermion pairs, first established in Ref. [3]: Not only is the purity $P$ a quantitative indicator for bosonic behaviour [3, 12, 13, 24], but so is the geometric measure of entanglement [30], which can be expressed here as a function of $\lambda _1$.

Depending on the application, the single-fermion purity $P$, the largest eigenvalue $\lambda _1$ of the single-fermion density matrix ${\hat{\rho }}_{(a/b)}$, or both may be known. We can formulate a clear hierarchy: Knowledge of $P$ is more valuable than the knowledge of $\lambda _1$ alone, whereas the combination can greatly enhance the bounds, depending on the value of the involved parameters. The effect of compositeness is observable in any physical observable that is affected by the commutation relation (22), such as, e.g. bosonic signatures in multiparticle interference [15].

Our method can be extended to formulate even stronger bounds that depend on the purity $P$ and on the $m$ largest Schmidt coefficients $\lambda _1 \ge \lambda _2 \ge \ldots \ge \lambda _m$: In close analogy to the procedure in [24] (see Appendix 1 and 2), minimising and maximising distributions can be constructed, and the resulting normalisation factors can be computed. The increased accuracy will, however, come at the expense of an increased computational cost, since a larger number of distinct Schmidt coefficients (up to $m+2$ when we fix the $m$ largest coefficients and the purity $P$) also leads to a larger number of sums when Eq. (17) is applied.

Another desideratum is the extension of the present bounds to multifermion systems in order to characterise, e.g. $\alpha$-particles in extreme environments [34, 35]. The absence of the Schmidt decomposition, Eq. (2), for multipartite states [4] makes this task, however, rather challenging. In particular, a simple combinatorial interpretation of the normalisation constant seems to be excluded for such composites.

Appendices

Appendix 1: Minimising distribution

For completeness, we reproduce the proofs from the Appendix of Ref. [24] in the Appendices 1 and 2, adapting the argument to our situation in which not only the purity $P$ is fixed, but also the largest Schmidt coefficient $\lambda_1$.

1.1 Uniforming operation

Following an analysis of the birthday problem with non-uniform birthday probabilities [32], we define a uniforming operation $\varGamma ^{u}$ on the distribution $\varvec{\Lambda }$ that can modify three selected $\lambda _j$ with indices ${2 \le j_1 < j_2 < j_3 \le S}$ (i.e. the operation never acts on the first Schmidt coefficient $\lambda _1$, since its value is fixed, by assumption). We will show that this operation always decreases $\chi _N$, and specify the distribution $\varvec{\Lambda }_{\text {min}}(P, \lambda _1)$ that remains invariant under the application of $\varGamma ^u$. This distribution thus minimises $\chi _N^{\varvec{\Lambda }}$ under the constraints $(P,\lambda _1)$.

The operation $\varGamma ^u$ modifies three coefficients in a distribution,

$$\begin{aligned} \varGamma ^u: ( \lambda _{j_1}, \lambda _{j_2},\lambda _{j_3} ) \rightarrow ( \lambda ^u_{j_1}, \lambda ^u_{j_2},\lambda ^u_{j_3} ) , \end{aligned}$$

(50)

such that it leaves

$$\begin{aligned} K_1&= \lambda _{j_1} + \lambda _{j_2} + \lambda _{j_3} , \nonumber \\ K_2&= \lambda _{j_1}^2 + \lambda _{j_2}^2 + \lambda _{j_3}^2 , \end{aligned}$$

(51)

invariant, and, consequently, also $\sum _{j} \lambda _j=1$ and $\sum _j \lambda _j^2=P$. The third power sum, $M(3)=\sum _j \lambda _j^3$, on the other hand, is changed by $\varGamma ^u$. Specifically,

$$\begin{aligned} \lambda _{j_1}^u = \lambda _{j_2}^u&= \frac{1}{6} \left( 2 K_1 + \sqrt{6 K_2-2 K_1^2} \right) \nonumber ,\\ \lambda _{j_3}^u&= \frac{1}{3} \left( K_1 - \sqrt{6 K_2-2 K_1^2} \right) . \end{aligned}$$

(52)

In the case $K_1^2 <2 K_2$, in order to avoid $\lambda _{j_3}^u<0$, we need to set

$$\begin{aligned} \lambda _{j_1/j_2}^u&= \frac{1}{2} \left( K_1 \pm \sqrt{2 K_2-K_1^2}\right) , \\ \lambda _{j_3}^u&= 0 \nonumber . \end{aligned}$$

(53)

1.1.1 The product $\lambda _{j_1} \lambda _{j_2}\lambda _{j_3}$ decreases under $\varGamma ^u$

It holds

$$\begin{aligned} \lambda _{j_1}^u \lambda _{j_2}^u \lambda _{j_3}^u \le \lambda _{j_1} \lambda _{j_2} \lambda _{j_3} . \end{aligned}$$

(54)

Proof

We write the left- and right-hand side of (54) in terms of $K_1, K_2$ and $\lambda _{j_1}$

$$\begin{aligned}&\lambda _{j_1}^u \lambda _{j_2}^u \lambda _{j_3}^u \nonumber \\&\quad = \left\{ \begin{array}{ll} \frac{1}{108} \left( K_1-\sqrt{6 K_2-2 K_1^2}\right) &{} \\ \times \left( 2 K_1+\sqrt{6 K_2-2 K_1^2}\right) ^2 &{}\hbox { for } K_1^2 > 2 K_2 \\ 0 &{}\hbox { for } K_1^2 \le 2 K_2 \end{array} \right. \\&\lambda _{j_1} \lambda _{j_2} \lambda _{j_3}= \frac{1}{2} \lambda _{j_1} \left( 2 \lambda _{j_1}^2-2 \lambda _{j_1} K_1+K_1^2-K_2 \right) \nonumber \end{aligned}$$

(55)

Given $K_1$ and $K_2$, the original $\lambda_{j_2/j_3}$ become functions of $\lambda _{_1},$

$$\begin{aligned} \lambda _{{j_2}/{j_3}} = \frac{1}{2} \left( K_1 - \lambda _{j_1} \pm \sqrt{2 \lambda _{j_1} K_1 - K_1^2 - 3 \lambda _{j_1}^2 + 2 K_2} \right) \nonumber \end{aligned}$$

(56)

The requirement $\lambda _{j_1} \ge \lambda _{{j_2}} \ge \lambda _{{j_3}} \ge 0$ imposes

$$\begin{aligned} \frac{ K_1}{3} + \frac{ \sqrt{3 K_2 - K_1^2}}{3\sqrt{2}}&\le \lambda _{j_1} \le \frac{ K_1}{3} +\frac{ \sqrt{6 K_2 -2 K_1^2} }{3}. \end{aligned}$$

(57)

The values of $\lambda _{j_1}$ constrained to this interval then always fulfil Eq. (54). $\square$

1.1.2 $\chi _N^{\varvec{\Lambda }}$ decreases upon application of $\varGamma ^u$

Upon application of $\varGamma ^u$, the normalisation constant $\chi _N$ and the normalisation ratio $\chi _{N+1}/\chi _N$ can only decrease:

$$\begin{aligned} \chi _{N}^{\varGamma ^{u}(\varvec{\Lambda }) }&\le \chi _{N}^{\varvec{\Lambda }} , \end{aligned}$$

(58)

$$\begin{aligned} \frac{\chi _{N+1}^{\varGamma ^{u}(\varvec{\Lambda }) } }{\chi _{N}^{\varGamma ^{u}(\varvec{\Lambda }) } }&\le \frac{ \chi _{N+1}^{\varvec{\Lambda }} }{ \chi _{N}^{\varvec{\Lambda }}} . \end{aligned}$$

(59)

To ease notation in the following, we exemplarily use $j_1=2,\, j_2=3,\, j_3=4$, and set

$$\begin{aligned} {\tilde{\chi }}_N&= \chi _N^{(\lambda _1, \lambda _5, \ldots , \lambda _S)}, \end{aligned}$$

(60)

which allows us to write $\chi _N$ as

$$\begin{aligned} \chi _N&= \lambda _2 \lambda _3 \lambda _4 \cdot {\tilde{\chi }}_{N-3} +(\lambda _2 \lambda _3 +\lambda _4 \lambda _3+\lambda _2 \lambda _4) {\tilde{\chi }}_{N-2} \nonumber \\&+(\lambda _2+\lambda _3+\lambda _4) {\tilde{\chi }}_{N-1}+ {\tilde{\chi }}_{N} . \end{aligned}$$

(61)

The terms

$$\begin{aligned} \lambda _2 \lambda _3 +\lambda _4 \lambda _3 +\lambda _2 \lambda _4&= \frac{1}{2} \left( K_1^2 - K_2 \right) , \\ \lambda _2+\lambda _3+\lambda _4&= K_1 , \end{aligned}$$

(62)

and ${{\tilde{\chi }}}_k \in \{ N-3, \dots , N \}$ remain invariant under the application of $\varGamma ^{u}$, whereas the product $\lambda _2 \lambda _3 \lambda _4$ decreases, due to Eq. (54). Consequently, also $\chi _N^{{\boldsymbol\Lambda }}$ decreases upon the application of $\varGamma ^u$.

Using $\chi _{N+1} \le \chi _{N}$, one can easily show in analogy to Ref. [24] that the inequality (58) is inherited by the normalisation ratio (59). $\square$

1.2 Properties of the minimising distribution

The distribution $\varvec{\Lambda }_{\text {min}}(P,\lambda _1)$ that minimises $\chi _N$ for fixed $\lambda _1$ and $P$ should remain invariant under the application of $\varGamma ^u$, for all choices of $2 \le j_1, j_2, j_3 \le S$. By the definition of $\varGamma ^u$, we see that any three coefficients with $\lambda _{j_1} > \lambda _{j_2} = \lambda _{j_3}$ never constitute a fixed point of $\varGamma ^u$. Therefore, the invariant distribution is of the form

$$\begin{aligned} \lambda _1 \ge \lambda _2=\ldots = \lambda _{S-1} \ge \lambda _S . \end{aligned}$$

(63)

It coincides with the distribution found in Ref. [23].

Appendix 2: Maximising distribution

1.1 Peaking operation

With $K_1$ and $K_2$ defined as in Eq. (51) above, we define the peaking operation $\varGamma ^p$ as follows [24]: For $K_1+\sqrt{6 K_2-2K_1^2} \le 3 \lambda _1$, we set

$$\begin{aligned} \lambda _{j_1}^{p}&= \frac{1}{3} \left( K_1 + \sqrt{6 K_2-2 K_1^2} \right) , \nonumber \\ \lambda _{j_2}^{p}=\lambda _{j_3}^{p}&= \frac{1}{6} \left( 2 K_1 - \sqrt{6 K_2-2 K_1^2} \right) . \end{aligned}$$

(64)

If $K_1+\sqrt{6 K_2-2K_1^2} > 3 \lambda _1$, the above definition leads to $\lambda _{j_1}^{p}> \lambda _1$, which we excluded by assumption. In this case, we define alternatively

$$\begin{aligned} \lambda _{j_1}^{p}&= \lambda _1, \\ \lambda _{j_2/j_3}^{p}&= \frac{ K_1 - \lambda _1 \pm \sqrt{2 (K_2 -\lambda _1^2) -(K_1-\lambda _1)^2 } }{{2}} , \nonumber \end{aligned}$$

(65)

for which $\lambda _1 = \lambda _{j_1}^p \ge \lambda _{j_2}^p \ge \lambda _{j_3}^p \ge 0$. In full analogy to the discussion in Appendix 1, one shows that

$$\begin{aligned} \chi _N^{\varvec{\Lambda }} \le \chi _N^{\varGamma ^p(\varvec{\Lambda })} , \qquad \frac{\chi _{N+1}^{\varvec{\Lambda }} }{\chi _N^{\varvec{\Lambda }} } \le \frac{\chi _{N+1}^{\varGamma ^p(\varvec{\Lambda })} }{\chi _N^{\varGamma ^p(\varvec{\Lambda })} } , \end{aligned}$$

(66)

i.e. the normalisation factor and ratio increase under the application of $\varGamma ^p$.

1.2 Properties of the maximising distribution

The distribution $\varvec{\Lambda }_{\text {max}}(P,\lambda _1)$ that maximises $\chi _N$ for fixed $\lambda _1$ and $P$ is obtained as follows: We maximise the multiplicity of $\lambda _1$ in $\varvec{\Lambda }$, i.e. $\lambda _1$ is repeated $L-1$ times, with $L=\lceil P/\lambda _1^2 \rceil$. The coefficients then need to fulfil

$$\begin{aligned} \lambda _1=\ldots = \lambda _{L-1} \ge \lambda _L \ge \lambda _{L+1}&= \ldots = \lambda _S , \end{aligned}$$

(67)

to ensure that $\varvec{\Lambda }_{\text {max}}(P,\lambda _1)$ be a fixed point of $\varGamma ^p$. Again, the distribution coincides with the one found in Ref. [23].