1 Introduction

Since the availability of high-power lasers, high-harmonic generation (HHG) based upon nonlinear Compton scattering (NLCS) from free electrons in strong laser fields has drawn considerable attention [1–14]. This is not only because it is a fundamental non-perturbative laser-induced phenomena, but also because it is a prospective X-ray or gamma-ray source [15–18] with remarkable performances in terms of tunability. Moreover, the free-electron laser interaction is very clean without other uncontrollable physical processes such as ionizations and collisions, which happen in the interaction between lasers and atoms or plasmas. In recent years, the observation of NLCS in some experiments [19–22] also renew the interest in its theoretical study.

The main aim of this paper is to investigate how the effect of the laser intensity gradients change the radiation of free electron in strong laser field. It is well-known that there is a cycle-averaged force on a charged particle in a spatially inhomogeneous laser field. It is associated with a time-independent potential energy called ponderomotive potential, which is due to the laser intensity gradient in an oscillatory field. After the presence of such ponderomotive potential was first proposed in 1957 by Boot and Harvie [23, 24], it is well-known for the last four decades that the potential could have a significant effect on the matter interacting with the laser field, such as particle acceleration [25], trapping and cooling of the atoms [26], high-field photoionization of atoms [27], self-focusing in plasma [28] and HHG [29, 30]. In the classical framework, the mechanical motion of electrons in a strong laser field will be changed if the ponderomotive potential is taken into account due to the limited spatial dimensions of the laser focus, which leads to the ponderomotive broadening of the radiation spectrum [29]. But, so far few works are done to study the role of the ponderomotive effects on the radiation spectrum based on a quantum theory [29, 30, 37].

To gain a clear idea of the influence by the laser intensity gradients on the HHG spectrum from free electrons in strong laser fields, we start from the scattering of the electron Volkov state by the ponderomotive potential of the laser beam. The corresponding cross section is calculated as a second-order quantum electrodynamics (QED) laser-assisted process similar to laser-assisted bremsstrahlung, where an charged particle scatters by the field of a nucleus in a background strong laser field [31–36].

For notations in this paper, the four-vector product is denoted by \(a\cdot b=a^0b^0-\varvec{ab}\) and the Feynman dagger is \(/\!\!\!A=\gamma \cdot A\). The Dirac adjoint is denoted by \(\overline{u}=u^{\dagger } \gamma ^0\) for a bispinor u and \(\overline{F}=\gamma ^0 F^{\dagger }\gamma ^0\) for a matrix F.

The outline of this paper is the following. First, we will introduce the scattering model and derive the theoretical expression for the cross section of the electron radiation. Then, the numerical estimation of the cross section and the corresponding analyses will be provided in Sect. 3. Concluding remarks are reserved for Sect. 4.

2 Theoretical derivation of the scattering cross section

We begin by introducing our scattering mode: Consider there are two monochromatic laser pulse in space. The first one propagates along z axis, of which the duration is long enough and the field intensity so strong that it can be modeled by a background classical plane wave field, described by a four-dimension vector potential \(A^{\mu }\):

$$\begin{aligned} {A^{\mu }}&= A_0[{\delta }\cos \phi {\epsilon _1}^\mu +(1-\delta ^2)^{1/2}\sin \phi {\epsilon _2}^\mu ], \end{aligned}$$
(1)

Here, with the phase factor \(\phi =k\cdot x\), in which \(x\) is the position vector, and the four wave vector is related to \(k^\mu =\frac{\omega _0}{c}(1,0,0,1)\) with \(\omega _0\) denoting the wave propagation direction and laser frequency, respectively. The laser is circularly polarized for \(\delta =1/\sqrt{2}\) and linearly polarized for \(\delta =0,\pm 1\). We define two polarization vectors \(\epsilon _1\), \(\epsilon _2\), satisfying \(\epsilon _i\cdot k=0,\, \epsilon _i\cdot \epsilon _j =\delta _{ij}\) \((i,j=1,2)\). The laser intensity can be easily described by a dimensionless parameter \(Q=eA_0/(mc^2)\), which is usually called laser intensity parameter. In the nonrelativistic regime, the characteristic velocity and energy for an electron moving in such an electromagnetic field is \(v\sim {eA_0/(mc)}\) and \(E\sim {e^2A_0^2/(mc^2)}\), so relativistic treatment is necessary if \(v\sim c\) and \(E\sim {mc^2}\) is satisfied. That is to say the motion of the electron will become relativistic for \(Q\sim 1\). In the optical regime (\(\hbar \omega \approx 1\,\hbox {eV}\)), the corresponding laser intensity is about \(10^{18}\,\hbox {W}/\hbox {cm}^2\) for \(Q\sim 1\), which has been achieved in the last decade.

Fig. 1
figure 1

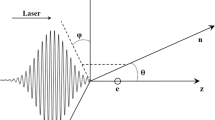
The scattering geometry: the incoming electron with four momentum \(p_i\) have a \(90^\circ\) collision with a plane laser field while scattering by a time-independent ponderomotive potential \(A_G\). The final electron with \(\Pi _f\) and the emitted photon with \(k^\prime\) are projected onto the xz plane in this figure; \(\theta _f\) and \(\theta ^{\prime }\) denotes the scattering angle of the outgoing electron and the emitted photon, respectively

Full size image

The second field is a tightly focused laser pulse propagating opposite the first one, which can be described by the lowest-order axicon Gaussian fields with a envelop factor \(g(\phi )=e^{\left( -{\phi ^2}/{(\Delta \phi )}\right) }\). It is far less intense than the first one (the intensity is described by another dimensionless parameter \(Q_G\)) but much rapidly oscillatory. The electron will be assumed to be moving with a momentum p in the direction perpendicular to z axis, say, x axis. When the electron is placed in the two laser wave field, it will be mainly driven by the longer-wavelength laser. The interaction of the electron with the plane wave laser will be treated exactly by introducing the well-known Volcov state. That is to say, the “dressed” electron will have an effective momentum \(\Pi =p+\frac{e^2A_0^2}{4c^2(p\cdot k)}\) with a corresponding effective mass \(m^{\prime }=m\sqrt{1+\frac{Q^2}{2}}\). While the main effect of the Gaussian laser pulse on the electron can be described by an time-averaged potential in view of its low intensity and fast oscillation (here, we do not care about the high-frequency part of the radiation caused by the fast oscillation). We assume that the relativistic electron moves so fast that the envelop factor is almost time independent. The effective pondermotive potential can be described by:

$$\begin{aligned} U_p=\frac{mc^2}{4}{Q_G}^2e^{-\frac{\varvec{r}_\bot ^2}{{b_0}^2}-\frac{z^2}{{b_1}^2}} \end{aligned}$$
(2)

The corresponding four-vector potential can be written as:

$$\begin{aligned} A^{\mu }_p=\frac{U_p}{e}\delta ^{\mu 0} \end{aligned}$$
(3)

where the Fourier-transformed pondermotive potential is given by:

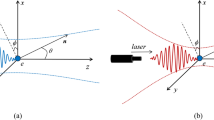
$$\begin{aligned} A^{\mu }_p(\varvec{q})=\frac{mc^2\pi ^{3/2}}{4e} {Q_G}^2 {b_0}^2 b_1 \delta ^{\mu 0}e^{-\frac{{b_0}^2}{4}\varvec{q}_\bot ^2-\frac{{b_1}^2}{4}{q_z^2}} \end{aligned}$$
(4)

Here, \(\varvec{r}_\bot\) and \(\varvec{q}_\bot\) refers to the position and momentum in the plane perpendicular to the propagation dirction, respectively, while is related to the beam waist and is decided by the pulse duration. Considering the high-frequency character of the pulse, which means a small wavelength, the paraxial approximation of the laser pulse can be acceptable confidently. Since \(Q_G\ll Q\) , we will treat the pondermotive potential as perturbation. The whole scattering configuration can be seen in Fig. 1 ,and it can be described by two Feynman diagrams shown in Fig. 2.

Fig. 2
figure 2

Feynman diagrams describing laser-assisted bremsstrahlung. The laser-dressed electron and laser-dressed electron propagator are denoted by a zigzag line on top of the straight line. The Coulomb field photon is drawn as a dashed line, and the bremsstrahlung photon as a wavy line

Full size image

It is obvious that the interaction of electron with the intense plane laser wave will leads to discrete line at a given harmonic on the spectrum if the second weak pulse is absent. The scattering process is called laser-induced Compton scattering, or NLCS for its nonlinear nature, which has been widely studied since the invention of laser in 1960 [13–16]. The frequencies of the emitted harmonics are determined from the energy-momentum conservation laws, which involve both the incident electron condition and laser parameters. Here, we wonder the effect of the pondermotive potential on the discrete radiation spectrum.

In order to calculate the differential cross section of the second-order laser-assisted process, we begin by employing the well-known Volkov state to describe the initial and final electron state:

$$\begin{aligned} \psi _{p,r}&= \frac{1}{V}\sqrt{\frac{mc}{\Pi ^0}}\zeta _p(x)u_r(p) \end{aligned}$$
(5)
$$\begin{aligned} \zeta _p(x)&= \left( 1+\frac{e/\!\!\!k/\!\!\!A}{2p\cdot k}\right) e^{iS} \end{aligned}$$
(6)
$$\begin{aligned} S&= -\frac{\Pi \cdot x}{\hbar }-\frac{e^2A_0^2}{8\hbar c^2(p\cdot k)}(2\delta ^2-1)\sin 2\phi +\frac{eA_0}{\hbar c(p\cdot k)}\nonumber \\&\quad \times \big [\delta ({p}\cdot {\epsilon _1})\sin \phi -(1-\delta ^2)^{1/2}({p}\cdot {\epsilon _2})\cos \phi \big ]. \end{aligned}$$
(7)

Here, \(u_r(p)\) the free Dirac spinor. Here, we employ a box normalization with a normalization volume V.

Then, the corresponding transition amplitude can be written as:

$$\begin{aligned} S_{fi}&= -\frac{e^2}{\hbar ^2 c^2}\int \hbox {d}x^4\hbox {d}y^4\bar{\psi }_{p_f,r_f}(x) \left[ /\!\!\!A_c(x)iG(x-y)/\!\!\!A_G(y)\right. \nonumber \\&\quad \left. +/\!\!\!A_G(x)iG(x-y)/\!\!\!A_c(y)\right] \psi _{p_{i},r_{i}}(y) \end{aligned}$$
(8)

\(A_c^\mu (x)=\sqrt{\frac{2\pi \hbar }{\omega ^\prime }}c{\epsilon _c}^\mu e^{i{k^\prime } x}\) stands for the four momentum of the emitted photo during the scattering process with \({\epsilon _c}^\mu\) the photon polarization vector and \(k^\prime =\frac{\omega ^\prime }{c}(1,\varvec{e_{k^\prime }})\) the wave vector, respectively. As the previous work [34, 35], here, we use the Dirac-Volkov propagator instead of the free-electron propagator in view of the strong laser field:

$$\begin{aligned} iG(x-y)=-\int \frac{\hbox {d}p^4}{(2\pi \hbar )^3(2\pi i)}\zeta _p(x)\,\frac{/\!\!\!p+mc}{p^2-m^2c^2}\,\bar{\zeta }_p(y) \end{aligned}$$
(9)

It has been proven [34] that the use of the Dirac-Volkov propagator is crucial to obtain correct numerical result in laser-modified QED process.

Here, we take average on the initial electron spin (i.e., the electron is unpolarized) and sum over the both final electron spin and emitted photon polarization. The differential cross section is calculated with the formula:

$$\begin{aligned} \hbox{d}\mathop {\sigma }\limits ^{\sim }=\frac{1}{2JT}\sum _{r_i,r_f,\varepsilon _c} \big |S_{fi}\big |^2\frac{V\hbox{d}^3\Pi _f}{(2\pi \hbar )^3}\frac{\hbox {d}^3k^\prime }{(2\pi )^3}. \end{aligned}$$
(10)

Here, T is the long observation time and \(J=\frac{c}{V}\frac{\varvec{\Pi }}{\Pi ^0}\) stands for the incoming particle flux. We have \(\hbox {d}^3\Pi _f=|\varvec{\Pi _f}|^2\hbox {d}\Omega _f=|\varvec{\Pi _f}|^2\sin \theta _f\hbox {d}\theta _f\hbox {d}\varphi _f\), \(\hbox {d}^3k^{\prime }=\frac{{\omega ^{\prime }}^2}{c^2}\hbox {d}\Omega ^{\prime }=\frac{{\omega ^{\prime }}^2}{c^2}\sin \theta ^{\prime }\hbox {d}\theta ^{\prime }\hbox {d}\varphi ^{\prime }\), where \(\Omega ^{\prime }\) and \(\Omega _f\) stands for the the solid angle of the emitted photon and electron, respectively. After a long but straight-forward deriving process, we finally write down the differential cross section as:

$$\begin{aligned} \frac{\hbox {d}\mathop {\sigma }\limits ^{\sim }}{\hbox {d}\omega ^\prime \hbox {d}\Omega ^\prime \hbox {d}\Omega _f}&= \frac{\alpha {Q_G^4}{b_0^4}}{8(4\pi )^4c^2}\left( \frac{m^2c^2}{\hbar ^2}b_1^2\right) \nonumber \\&\quad \times \;\sum _{n,\varepsilon _c}\frac{|\varvec{\Pi _f}|}{|\varvec{\Pi _i}|} e^{-\frac{{b_0}^2}{2}\varvec{q}_\bot ^2-\frac{{b_1}^2}{2}{q_z^2}}\nonumber \\&\quad Tr[\bar{R}_{fi,n}(p_f+mc)R_{fi,n}(p_i+mc)] \end{aligned}$$
(11)

where:

$$\begin{aligned} R_{fi,n}&= \sum _s M_{-n-s}\left( \Pi _f,\Pi ,/\!\!\!\epsilon _c,\eta ^1_{\Pi ,\Pi _f},\eta ^2_{\Pi ,\Pi _f}\right) \nonumber\\ &\quad\frac{i}{/\!\!\!p-mc} \bar{M}_{-s}\left( \Pi _i,\Pi ,\gamma ^0,\eta ^1_{\Pi ,\Pi _i},\eta ^2_{\Pi ,\Pi _i}\right) \nonumber \\&\quad +\sum _{s^\prime }M_{-n-s^\prime }\left( \Pi _f,\Pi ^\prime ,\gamma ^0,\eta ^1_{\Pi ^\prime ,\Pi _f},\eta ^2_{\Pi ^\prime ,\Pi _f}\right)\nonumber \\ &\quad \frac{i}{/\!\!\!p^\prime -mc} \bar{M}_{-s^\prime }\left( \Pi _i,\Pi ^\prime ,/\!\!\!\epsilon _c,\eta ^1_{\Pi ^\prime ,\Pi _i},\eta ^2_{\Pi ^\prime ,\Pi _i}\right) \end{aligned}$$
(12)

With the argument is defined as:

$$\begin{aligned} \eta ^1_{p_1,p_2}&= \frac{eA_0}{\hbar c}\delta \left[ \frac{{p_2}\cdot {\epsilon _1}}{k\cdot p_{2}}-\frac{{p_1}\cdot {\epsilon _1}}{k\cdot p_1}\right] \nonumber \\ \eta ^2_{p_1,p_2}&= -\frac{eA_0}{\hbar c}(1-\delta ^2)^{1/2}\left[ \frac{{p_2}\cdot {\epsilon _1}}{k\cdot p_{2}}-\frac{{p_1}\cdot {\epsilon _1}}{k\cdot p_1}\right] \end{aligned}$$
(13)

\(\Pi ,\Pi ^\prime\) is the four momentum of the intermediate electron in the Feynman diagrams shown in Fig. 2. They are determined by the conservation law, together with the four momentum q transfer from the pondermotive potential, which is given by the corresponding functions during the calculation process:

$$\begin{aligned} \Pi&= \pi _f-(n+s)\hbar k+\hbar k^\prime \nonumber \\ \Pi ^\prime&= \pi _i-s\hbar k-\hbar k^\prime \nonumber \\ \hbar q&= \pi _f-\pi _i+\hbar k^\prime -n\hbar k \end{aligned}$$
(14)

M is a \(4\times 4\) matrix with five arguments:

$$\begin{aligned} M_{s}(p_1,p_2,F,\eta ^1_{p_1,p_2},\eta ^2_{p_1,p_2})&= \left[ /\!\!\!F+\frac{e^2{A_0}^2}{8c^2}\frac{/\!\!\!k/\!\!\!F/\!\!\!k}{(p_i\cdot k)(p_2\cdot k)}\right] G^0_s(\alpha ,\beta ,\varphi )\nonumber \\&\quad +\frac{eA_0}{2c}\delta \left[ \frac{/\!\!\!\epsilon _1/\!\!\!k/\!\!\!F}{(p_1\cdot k)}+\frac{/\!\!\!F/\!\!\!k/\!\!\!\epsilon _1}{(p_2\cdot k)}\right] G^1_s(\alpha ,\beta ,\varphi )\nonumber \\&\quad +\frac{eA_0}{2c}(1-\delta ^2)^{1/2}\left[ \frac{/\!\!\!\epsilon _2/\!\!\!k/\!\!\!F}{(p_1\cdot k)}+\frac{/\!\!\!F/\!\!\!k/\!\!\!\epsilon _2}{(p_2\cdot k)}\right] G^2_s(\alpha ,\beta ,\varphi )\nonumber \\&\quad +\left( \delta ^2-\frac{1}{2}\right) \frac{e^2{A_0}^2}{4c^2}\frac{/\!\!\!k/\!\!\!F/\!\!\!k}{(p_i\cdot k)(p_2\cdot k)}G^3_s(\alpha ,\beta ,\varphi ) \end{aligned}$$
(15)

The generalized Bessel functions are given by:

$$\begin{aligned} G^0_s(\alpha ,\beta ,\varphi )&= \sum _n {J_{2n-s}(\alpha )J_n(\beta )e^{i(s-2n)\varphi }},\nonumber \\ G^1_s(\alpha ,\beta ,\varphi )&= \frac{1}{2}\big (G_{s+1}^0(\alpha ,\beta ,\varphi )+G_{s-1}^0(\alpha ,\beta ,\varphi )\big ),\nonumber \\ G^2_s(\alpha ,\beta ,\varphi )&= \frac{1}{2i}\big (G_{s+1}^0(\alpha ,\beta ,\varphi )-G_{s-1}^0(\alpha ,\beta ,\varphi )\big ),\nonumber \\ G^3_s(\alpha ,\beta ,\varphi )&= \frac{1}{2}\big (G_{s+2}^0(\alpha ,\beta ,\varphi )+G_{s-2}^0(\alpha ,\beta ,\varphi )\big ). \end{aligned}$$
(16)

With the corresponding argument:

$$\begin{aligned} \alpha&= [(\eta ^1_{p_1,p_2})^2+(\eta ^2_{p_1,p_2})^2]^{1/2}\nonumber \\ \beta&= \frac{Qm^2c^2}{8\hbar }(2\delta -1)\left( \frac{1}{k\cdot p_1}-\frac{1}{k\cdot p_2}\right) \nonumber \\ \varphi&= arctan\left( -\frac{\eta ^2_{p_1,p_2}}{\eta ^1_{p_1,p_2}}\right) \end{aligned}$$
(17)

The above differential cross section is related to the spontaneous photon in the frequency interval \(\hbox {d}\omega ^{\prime }\) within the solid angle \(\Omega ^{\prime }\) and the final electron within the solid angle \(\Omega _f\). But it is difficult to detect the photon and electron in the same time during an actual experiment. So we integrate the differential cross section over the scattering electron direction, by which leads to the doubly differential cross section only differential in the direction of the radiated photon and its frequency:

$$\begin{aligned} \frac{\hbox {d}\sigma }{\hbox {d}\omega ^\prime \hbox {d}\Omega ^\prime }=\int \frac{\hbox {d}\mathop {\sigma }\limits ^{\sim }}{\hbox {d}\omega ^\prime \hbox {d}\Omega ^\prime \hbox {d}\Omega _f}\hbox {d}\Omega _f \end{aligned}$$
(18)

As one of the characteristic feature of a second-order process, the resonance will happen when the intermediate electron fall within the mass shell. The physical interpretation, according to Roshchupkin [36], may be that the considered second-order process effectively reduces to two sequential first-order processes under certain resonance condition. In the paper, the two sequential lower processes are NLCS and static ponderomotive potential scattering, respectively. The corresponding resonance condition may be written as \(\Pi ^2={m^\prime }^2c^2\) or \({\Pi ^\prime }^2={m^\prime }^2c^2\). When resonance occurs, the scattering cross section will be divergent, which indicates that the perturbation method is not applicable in such situation. To avoid the problem, one has to introduce a small imaginary part of the mass which results from the high radiative correction, i.e., the self-energy of the laser-dressed electron, which is determined by the total probability of the Compton scattering in a laser wave \(W_c(k\cdot p)\): \(\Gamma _m(k\cdot p)=\frac{\Pi ^0}{2m}W_c(k\cdot p)\). Then, the shifted propagator reads:

$$\begin{aligned} &\frac{1}{p-mc}\nonumber\\&= \frac{\Pi +m^{\prime }c}{\Pi ^2-{m^\prime }^2c^2-i\frac{m}{\Pi _f^0c}(\hbar \omega ^{\prime }-(n+s)\hbar \omega _0)\Gamma _m(k\cdot \Pi _f)+im\Gamma _m(\hbar k\cdot k^{\prime })} \end{aligned}$$
(19)
$$\begin{aligned} &\frac{1}{p^{\prime }-mc}\nonumber\\&= \frac{\Pi ^{\prime }+m^{\prime }c}{{\Pi ^\prime }^2-{m^\prime }^2c^2+i\frac{m}{\Pi _f^0c}(\hbar \omega ^{\prime }-s\hbar \omega _0)\Gamma _m(k\cdot \Pi _i)-im\Gamma _m(\hbar k\cdot k^{\prime })} \end{aligned}$$
(20)

The inclusion of the imaginary part of the electron mass eliminates the resonance singularity, which enable us to evaluate the cross section numerically. Then, the resonance peak altitude is determined by the lifetime of the immediate electron. Actually, the calculation of \(\Gamma _m\) has been discussed in many papers, and we can easily obtain the imaginary mass by taking advantage of the corresponding results of our previous study.

3 Numerical results

Fig. 3
figure 3

The cross section for the low-order harmonics at emission angle \(\theta ^\prime =1^\circ\). Here, we consider an electron with initial energy 5 MeV collide with a circularly polarized laser with intensity parameter \(Q=17.8\) and is scattered by an effective ponderomotive potential for a \(90^\circ\) geometry. The ponderomotive potential is characterized by two parameter: b 0 = 5 μm, b 1 = 100 μm, describing the beam waist size and duration of the tightly focused laser pulse, respectively

Full size image

In this section, we will present the numerical results of the differential cross section referring to the case of \(90^\circ\) laser–electron interaction geometry shown in Fig. 1. We consider the plane wave laser to be circularly polarized with a frequency of \(\omega =1.17\,\hbox {eV}\) and the dimensionless parameter Q = 17.8, which is related to a laser intensity of \(7.58\times 10^{22}\,\hbox {W}/\hbox {cm}^2\). It should be emphasized that the numerical results in our presentation are more exploratory than systematic since we shall focus on the influence of ponderomotive potential due to the intensity gradients on the photon radiation. First, we start with the results for a tightly focused laser pulse with the parameters b 0 = 5 μm, b 1 = 100 μm, which means the pulse duration is very long (i.e., for a pulse with wavelength 0.1 μm , the duration is about 0.3 ps). The corresponding differential cross section of the radiated photon for an emission angle \(\theta ^{\prime }=1^\circ\) is shown in Fig. 3. As expected, high harmonics are generated and the positions of the resonances located in the spectrum coincide with those for NLCS. This is due to the fact that the resonant second-order process can effectively reduce to two sequent lower-order processes as mentioned before while the mechanism responsible for radiation of photons is the NLCS process. Furthermore, the main contribution of the cross section comes from \(\varvec{q}\approx 0\) at a resonance, which means there is nearly no momentum transfer between the electron and the ponderomotive potential. It is easy to find that the main influence due to the ponderomotive potential is the broadened spectrum compared with that of NLCS, which is in accordance with the conclusion based on a classical theory [30]. The magnitude of the spectrum drops fast when the energy of photon is away from resonance. From a mathematical point of view, that is because the differential cross section is subject to an exponential decay with respect to the transfer momentum q. So the spectrum broadening effects is determined both the parameter \(b_0\) and \(b_1\), or the pulse duration and the beam waist size.

Fig. 4
figure 4

The cross section for the fundamental harmonic at emission angle \(\theta ^\prime =1^\circ\). The condition is same with Fig. 3 except the parameter \(b_0\): 5 μm for full line and 10 μm for dot-dashed line

Full size image

Now, we proceed to investigate how the broadening effect depends on the laser pulse duration and the beam waist size. In Fig. 4, we compare the spectrum of fundamental harmonics for different beam waist size with same pulse duration. The cross section with b 0 = 5 μm is denoted by full line, whereas the dotted-dashed line denote the cross section with b 0 = 10 μm. Here, the magnitude of the cross section near resonance is a little larger for a broader beam waist size. This is probably because a laser with certain intensity has a great energy with the increase in the beam waist size. We can also see from the expression (11) that the differential cross section is proportional to the quartic of \(b_0\). But the peak falls off much more quickly for a larger beam waist size. This can be understood by considering that the differential cross section is determined exponentially by \(b_0\). The physical interpretation may be that the large beam waist leads to a less field gradient, which means a small ponderomotive potential effect. When the beam waist is so large that we can neglect the spatial gradient if we consider the interaction of the electron with laser field near its focus place, there will be almost no ponderomotive broadening at all. In the following,we shall refer to the spectra of different laser pulse by changing the parameter \(b_1\), as shown in Fig. 5. The difference is so small that it can be hardly visible. We thus find that the pulse duration plays only a minor role in the spectrum. That is probably because there is far less momentum transfer from the electron onto the ponderomotive potential in the laser propagation direction (i.e., \(q_z^2\approx 0\ll q_\bot ^2\)) for a \(90^\circ\) interaction geometry. Hence, there is almost no ponderomotive potential scattering in this direction.

Fig. 5
figure 5

The cross section for the fundamental harmonic at emission angle \(\theta ^\prime =1^\circ\). The condition is same with Fig. 3 except the parameter \(b_1\): b 1 = 100 μm for full line and b 1 = 150 μm for dot-dashed line

Full size image

Finally, we compare the results of different laser intensity of the circularly polarized plane wave field. The corresponding spectra are displayed in Fig. 6. It shows that the radiation for the plane wave field Q = 5 (corresponds to a intensity of \(3\times 10^{19}\,\hbox {W}/\hbox {cm}^2\)) is several magnitudes smaller than that for Q = 17.8 (corresponds to a intensity of \(7.58\times 10^{20}\,\hbox {W}/\hbox {cm}^2\)). But the broadening width of the spectra is similar for two different laser strengths. It confirmed the conclusion that the broadening effect has almost nothing to do with the plane wave field, but caused by the ponderomotive potential.

Fig. 6
figure 6

The cross section for the fundamental harmonic at emission angle \(\theta ^\prime =1^\circ\). The condition is same with Fig. 3 except the intensity of the plane wave laser: \(Q=17.8(7.58\times 10^{20}\hbox {W}/\hbox {cm}^2\)) for full line and \(Q=5(3\times 10^{19}\hbox {W}/\hbox {cm}^2)\) for dot-dashed line

Full size image

4 Summary

In this paper, we study the role of the field intensity gradients on the radiation spectrum emitting from the electron in the laser field. The whole scattering process is calculated as a laser-modified second-order QED process with resonances addressed. Consequently, it shows that the spectrum is broadening due to the ponderomotive effects compared with that of NLCS, with the positions of the resonance peak corresponding to the discrete harmonic frequencies of NLCS. Because the broadening of the spectrum line contains important information about the laser intensity gradient, it might provide us a feasible way to measure the width of the intense laser beam. In addition, the broadening effect is determined far more by the beam waist size than the pulse duration for the case of \(90^\circ\) incidence scattering geometry. Since the parameters of the corresponding laser field is readily accessible in the lab, it is hoped that these results could be submitted to the experiment test in the near future.