1 Introduction

Recent experimental progress in atomic physics allows us to manipulate ultracold atoms using micro-devices, so called atom chips [1–6]. The miniaturization and integration of trapping potentials achieved by the advanced nano-fabrication techniques enable versatile applications of ultracold atoms in quantum devices. For the full quantum control of an atomic state on atom chips, atoms should be confined very tightly near a current-carrying wire via a high magnetic field gradient so as to reach the quantization of motional states of atoms. This condition, however, causes a problem such that the number of confined atoms decays rapidly as the distance from a flowing current is decreased. It has been pointed out theoretically that the thermal noise of the current induces a spin-flip transition leading to a serious decay of atoms [7–11]. The elimination of undesirable current thermal noise is essential to the development of atom chips.

One successful solution was demonstrated by replacing the current-carrying wires that were made from conventional metals by superconducting wires [12–15], and this resulted in a significant reduction in atom number decay in more than one order of magnitude. Furthermore, the introduction of a superconductor enables completely different circuit designs for trapping atoms: an isolated piece of thin film [16–19] and a closed-loop circuit [20, 21]. The closed-loop circuit is particularly advantageous from a technical viewpoint for atom chips. We can drive persistent supercurrent inductively without any power supplies directly attached to the circuit [20, 21]. This current-driving technique significantly simplifies the circuit patterns and removes electric wire connections to the chip circuit. The isolated chip circuit is free from the noises in the environment: thermal noises from other room temperature circuits and power supplies. In addition, thanks to the heat-expansion-free property enabled by the zero resistivity of the isolated wires on a chip, the magnetic trapping potential produced by the persistent supercurrent is very stable showing negligibly small drifts in the potential minimum.

These features of a persistent-supercurrent atom chip directly benefit the future applications of ultracold atoms in the field of quantum technology. A magnetic waveguide produced by persistent supercurrent allows us to construct an ultrastable atom interferometer that is highly suitable for quantum metrology with extremely high precision. We can also create a platform consisting of a large number of microscopic atom traps toward quantum memories or quantum gates by designing an array of isolated closed-loop circuits. Furthermore, a noise-suppressed trap close to a chip has the ability to change the radial confinement of the trapping potential over a wide range. This has the advantage of making it possible to examine the quantum dynamics of atoms trapped in a quasi-one-dimensional potential for simulating the complicated many-body effects in low-dimensional systems [22, 23]. A Bose–Einstein condensate (BEC) on a persistent-supercurrent atom chip is an essential element for developing such quantum technology [24, 25].

In this article, we report the achievement of creating a BEC on a persistent-supercurrent atom chip. We applied the forced evaporative cooling directly to the magnetically trapped atoms on the chip. The condensation was verified by the time-of-flight (TOF) imaging of bimodal momentum distributions and also by a measurement of atom number decay in the trapping potential via three-body loss. The paper is organized as follows. In Sect. 2, we describe the experimental setup and detail the driving of persistent current. In Sect. 3, we show our results and discussion before summarizing our work in Sect. 4.

2 Experimental

2.1 Setup and current control

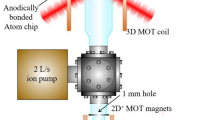
Our experimental setup consisted of a double chamber vacuum system with a glass cell pre-cooling chamber and an aluminum chip chamber with a liquid helium flow-type cryostat (Fig. 1a), as described in our previous reports [20, 21]. The superconducting chip used for our experiments was made from \(1.6\;\upmu\hbox{m}\)-thick magnesium diboride (MgB2) thin film grown by molecular beam epitaxy (MBE) on a sapphire substrate. MgB2 is a type II superconductor, the superconducting transition temperature T c is 39 K, the critical current density J c is \(\sim10^{11}\;\hbox{A}/\hbox{m}^{2}\), and the lower critical field H c1 is \(\sim 2 \times 10^{4}\;\hbox{A}/\hbox{m}\) [26–28]. This J c is about one order of magnitude larger than that of Niobium, which is often used in superconducting atom chips [13, 24]. The top of the MgB2 thin film was coated with a 60 nm gold layer to prevent radiation heating. The chip circuit was patterned with Ar+ milling into a 9-mm-square closed-loop strip (\(100\;\upmu\hbox{m}\) in width) with a z-shape at one corner (bottom right in Fig. 1b). The superconducting chip was mounted on the underside of a 4-cm-long sapphire chip mount that was attached to the bottom of a cold finger of the cryostat.

Fig. 1
figure 1

a Configuration of the double chamber vacuum system. The vacuum pumps and the atomic source are not shown. b Schematic bottom view of the superconducting closed-loop circuit

Full size image

A persistent supercurrent was induced in the closed-loop circuit with an inductive driving technique. Firstly, we applied a magnetic field H z to the closed-loop circuit parallel to the z-axis when the chip temperature T chip was higher than T c (T chip = 50 K). Then, the chip was cooled to a temperature below T c (T chip = 10 K) with the applied magnetic field. During this process, the magnetic flux inside the closed-loop circuit \(\Upphi_{\rm in}\) was fixed at \(\mu_{0} {\bf s} \cdot {\bf H}_{\rm z}\) when the circuit transited to the superconducting state, where μ 0 is the magnetic permeability of the vacuum and s is the area vector of the closed-loop circuit. Secondly, by turning off the applied magnetic field at the same temperature (<T c), a persistent current \(I_{\rm id} = \mu_{0} {\bf s} \cdot {\bf H}_{\rm z}/L\) was induced in the closed-loop circuit to conserve \(\Upphi_{\rm in}\) as illustrated in {i} and {ii} in Fig. 2a, where L is a constant corresponding to the inductance of the closed-loop circuit. As long as the chip temperature was kept below T c and the magnetic field applied after the superconducting transition was smaller than \(H_{\rm c1}, \Upphi_{\rm in}\) was conserved.

Fig. 2
figure 2

Schematic plot of the magnetic flux inside the closed-loop circuit for inducing a persistent current. a The case when H z was applied for setting \(\varPhi_{\rm in}.\) b The case when H z and H bias were applied for setting \(\varPhi_{\rm in}.\) {i} and {I} the flux for setting \(\varPhi_{\rm in}.\) The temperature of the chip was cooled from above T c to below T c with these conditions. {ii} and {II} the flux and current after turning off the applied magnetic field. {iii} and {III} the flux and current when the z-wire trap was constructed. With the sequence shown in b, the current of the z-wire trap can be controlled with |H z| alone independently of the bias magnetic field H bias

Full size image

To make a magnetic trap, we employed a conventional z-wire trap configuration [1] with a bias magnetic field H bias parallel to the y-axis. For technical reasons, perfect alignment of the bias magnetic field was difficult and there remained an unknown misalignment. With the misalignment, the flux inside the closed-loop circuit becomes \(\Upphi_{\rm in} = \mu_{0} {\bf s} \cdot {\bf H}_{\rm bias} + \Upphi^{\prime}\) when the z-wire trap is constituted, where \(\Upphi^{\prime}\) is a magnetic flux contributing to driving the persistent current. When \({\bf s} \cdot {\bf H}_{\rm bias}\) has a nonzero value, \(\Upphi^{\prime}\) becomes different from the initial \(\Upphi_{\rm in}\) (\(= \mu_{0} {\bf s} \cdot {\bf H}_{\rm z}\)), and the flowing z-wire current deviates from the initial value I id to I id − δI, where \(\delta I = \mu_{0} {\bf s} \cdot {\bf H}_{\rm bias}/L\), as illustrated in {ii} and {iii} in Fig. 2a. Thus, the current in the closed-loop circuit depends on the bias magnetic field, which includes an unknown misalignment, and also, the current cannot be measured directly. This makes it difficult to measure the bias magnetic field dependence of certain parameters while leaving the z-wire current unchanged. However, we can avoid the difficulty by employing the following current preparation technique.

Unlike the current, the magnetic flux inside the closed-loop circuit is fixed before constructing the z-wire trap. Therefore, when setting \(\Upphi_{\rm in}\) we applied H z and H bias as illustrated in {I} in Fig. 2b. When H z and H bias were turned off, a current of I id + δI was induced ({II} in Fig. 2b). Then, H bias was applied again to construct the z-wire trap, and the current in the z-wire became \(I_{\rm id} = \mu_{0} {\bf s} \cdot {\bf H}_{\rm z}/L\) ({III} in Fig. 2b). With this technique, we were able to control the current of the z-wire trap only by controlling |H z| independently of the bias magnetic field. In this way, we avoided the current control problem and we could investigate the configuration of the magnetic field near the chip surface as detailed in the next section.

2.2 Trapping and measurements

With 10 s of pre-cooling, we accumulated a cloud of approximately \(10^{9}\;^{87}\hbox{Rb} |F, m_{\rm F}\rangle = |2, 2\rangle\) atoms at \(200\;\upmu\hbox{K}\) in a quadrupole magnetic trap (QMT). With a mechanical translation of the QMT in the horizontal direction to the chip chamber, we brought the trapped atomic cloud 4 mm below the superconducting chip. Next, the QMT center was shifted toward the z-shaped wire of the chip circuit in 4 s by gradually increasing a magnetic field H up parallel to the z-axis. In the final stage of increasing H up, the bias magnetic field H bias was also increased to make a trapping potential. Finally, the QMT field and H up were turned off in 70 ms. At this point ∼107 atoms at 200 μK had been captured in the z-wire trap. Typically, they were trapped \(480\;\upmu {\rm m}\) below the chip surface with μ 0 H bias = 1.5 mT and I id = 4.4 A. Note that I id was significantly large in our experiment thanks to the larger critical current in comparison with the similar experiments [13, 24]. This enabled us to generate the sufficiently tight trapping potential for creating BEC at the distance far from the chip surface. Next, H bias was increased to a given value in 500 ms, and forced evaporative cooling was started to increase the phase-space density of the atomic cloud with a radio frequency magnetic field, which was generated by a coil normal to the chip surface (along the y-axis) so as to avoid the penetration of the field into the closed-loop circuit. This arrangement of the coil was essential to achieve BEC with a persistent-supercurrent atom chip. The radio frequency was swept from 20 MHz to \(\sim1.7\;\hbox{MHz}\) in \(\sim 20\;\hbox{s}\). During the final 100 ms of the evaporative cooling, the frequency sweeping was accelerated to obtain a BEC by overcoming the serious three-body loss [29, 30].

The atomic cloud was illuminated with a resonant imaging pulse with a \(100\;\upmu\hbox{s}\) time duration, and an absorption image was obtained with a charge-coupled device camera. TOF images were taken with a beam injected parallel to the chip surface. The beam was then tilted by 5° from the TOF configuration in order to measure the distance Z trap between the center of the atomic cloud and the chip surface [5, 21]. The TOF image was taken 15 or 32 ms after releasing the atomic cloud by turning off the bias magnetic field. Unlike a standard TOF measurement, the persistent current was left running because it cannot be terminated quickly even with a laser-injected thermal-switching technique [20]. For this reason, the atomic cloud released from the trap was accelerated by both the gravitational field and the residual magnetic field of the persistent current, resulting in a small distortion in the TOF images.

For decay measurements, an almost pure BEC without thermal fraction was confined in the potential for less than 2 s. During this period, we applied a radio frequency shield in order to minimize the loss of trapped atoms by collisions with the background gas in the trapping volume [31] and also with the heated atoms generated by inelastic collisions [32, 33]. The radio frequency was set to the potential depth of \(0.7\;\upmu\hbox{K}\), which ensured that we could measure the three-body loss purely without an influence of collisional avalanche [33]. The loss due to the instability of the trap bottom was negligible, because the long-term drift of the bottom (including shot-to-shot fluctuations) was evaluated to be less than \(0.1\;\upmu\hbox{K}\), which was sufficiently smaller than the potential depth.

3 Results and discussion

In this section, first we analyze the magnetic trapping potential produced by both a persistent supercurrent and a misaligned bias magnetic field. This is an essential procedure in our present experiments using a superconducting closed-loop circuit. We then demonstrate the achievement of BECs in two different ways: a TOF measurement and a decay measurement. We confirm the quantum statistical properties of condensed atoms in the three-body loss process via a quantitative comparison of measured data and theoretical simulations.

3.1 Magnetic trapping potential

As explained in the previous section, there was an unknown misalignment between the bias magnetic field and the closed-loop circuit. This required a careful analysis of the configuration of the magnetic field produced near the chip surface. We describe the method for calculating the magnetic trapping potential in our experiments. We define the direction of H bias by using the two angles ϕ and θ as shown in Fig. 3, where P is a projection of H bias onto the xy-plane, ϕ is the angle between H bias and P, and θ is the angle between P and the y-axis, i.e., \({\bf H}_{\rm bias} = (H_x,H_y,H_z) = H_{\rm bias}(\cos \phi \sin \theta, \cos \phi \cos \theta, \sin \phi)\). The produced magnetic field is given as a function of five variables: H bias, ϕ, θ, I id, and H′. Here, H′ is the x-component of the residual magnetic field H′, which mainly consisted of the field of the permanent magnets of ion pumps. The magnitude |H′| was roughly evaluated to be on the order of 0.1 mT. We approximately neglected y- and z-components of H′; the numerical simulation showed that the magnetic trapping potential was very insensitive to these components as a characteristic of the Ioffe–Pritchard potential. Experimentally, H bias could be determined with a Hall probe magnetometer. The unknown variables I id, ϕ, θ, and H′ should be evaluated indirectly from measurements of quantities that characterize the magnetic trapping potential. In this regard, the following two facts simplified the problem. As mentioned in the previous section, we compensated for the contribution of the tilted bias field H bias to I id in the process of persistent-supercurrent induction. Furthermore, the residual magnetic field in the environment H′ was expected to be almost constant in our experiments and did not induce any supercurrents in the closed-loop circuit. Thus, the variable I id was independent of H bias, ϕ, θ, and H′.

Fig. 3
figure 3

Schematic view of the closed-loop circuit with a z-shaped wire configuration and H bias. O represents the origin of the coordinate and P a projection of H bias onto the xy-plane. ϕ represents the angle between H bias and P, and θ between P and y-axis

Full size image

We measured both Z trap [5, 21] and the minimum value of the trapping potential by varying H bias under the condition that I id was fixed at a certain value and then quantitatively compared the experimental results with calculations based on the Biot-Savart law using all the unknown variables as fitting parameters. Figure 4 shows the measurement results of Z trap as a function of μ 0 H bias. Filled circles represent the experimental data of Z trap obtained by changing μ 0 H bias from 2.7 to 9.5 mT under the condition of \(\mu_0 |{\bf H}_{\rm z}| = 1.0\;\hbox{mT}\). The measured Z trap values monotonically decrease as μ 0 H bias increases. We carried out numerical calculations and found that the calculated curves were nearly independent of H′ and θ values, which means that both I id and ϕ can be evaluated almost selectively via the measurement data of Z trap. The lines in Fig. 4 correspond to the calculated results using θ = 4° and \(\mu_{0}H^{\prime} = -0.2\;\hbox{mT}\), and four sets of I id and ϕ. From (i), (ii), and (iii), the dependence on H bias was highly sensitive to the I id value. Furthermore, by comparing between (i) and (iv), we see that the ϕ value slightly modifies the curvature of Z trap − μ 0 H bias curve. These properties made it possible for us to evaluate I id and ϕ to fit the measurement results of Z trap. We obtained \(I_{\rm id} = 4.4\;\hbox{A}\) and ϕ = 12° at \(\mu_0 |{\bf H}_{\rm z}| = 1.0\;\hbox{mT}\).

Fig. 4
figure 4

Z trap as a function of μ 0 H bias. Filled circles are the experimental data. Lines represent the calculated results with θ = 4°, μ 0 H′ =  − 0.2 mT, and four sets of I id and ϕ: (i) (I id, ϕ) = (3.9 A, 0°) for the dotted line, (ii) (4.4 A, 0°) for the dashed line, (iii) (4.9 A, 0°) for the dash-dotted line, and (iv) (4.4 A, 12°) for the solid line, respectively

Full size image

The remaining two variables θ and H′ were determined via the minimum value of the magnetic trapping potential that was measured as the highest radio frequency ν0 at which all the atoms vanished during evaporative cooling process [34, 35]. In Fig. 5, the filled circles represent the experimental data of ν0 when μ 0 H bias was changed from 1.5 to 6.3 mT keeping \(\mu_0 |{\bf H}_{\rm z}|=1.0\;\hbox{mT}\). ν0 gradually increased from 1.7 to 2.6 MHz as μ 0 H bias was increased. The magnetic potential was very stable thanks to the persistent supercurrent. The uncertainty of ν0 was less than 5 kHz. The lines in Fig. 5 depict the calculated results of ν 0 using \(I_{\rm id} = 4.4\;\hbox{A}, \phi =12^{\circ}\), and the four choices of both θ and μ 0 H′ values. The dotted line (i) calculated with \((\theta, \mu_{0}H^{\prime})=(0, 0\;\hbox{mT})\) showed a completely different dependence on μ 0 H bias in comparison with the measurement results. However, as demonstrated by both the dashed line (ii) and the dashed-dotted line (iii), even a small θ value greatly modified such dependence. We obtained the solid line (iv) that fitted the measured data by further choosing an appropriate μ 0 H′ value. All the unknown variables were determined so that they provided a good fit with the experimental results for Z trap and ν0 simultaneously in a self-consistent way, and we finally obtained \({\theta} = 4.15^{\circ}, {\phi} = 12^{\circ}, \mu_{0} H^{\prime} = -0.16\;\hbox{mT}\) and \(I_{\rm id} = 4.4\;\hbox{A}\) for \(\mu_0 |{\bf H}_{\rm z}|=1.0\;\hbox{mT}\). The procedures explained above allowed us to fully calculate the magnetic trapping potential produced on the chip as a function of H bias and I id.

Fig. 5
figure 5

ν0 as a function of μ 0 H bias. Filled circles represent the experimental data. Lines correspond to theoretical calculations using I id = 4.4 A, ϕ = 12°, and the four different choices of two unknown variables: (i) (θ,  μ 0 H′) = (0°, 0 mT) for the dotted line, (ii) (2°, 0 mT) for the dashed line, (iii) (4.15°, 0 mT) for the dash-dotted line, and (iv) (4.15°, − 0.16 mT) for the solid line, respectively

Full size image

3.2 TOF measurement

We realized BECs in a magnetic trapping potential produced with \(\mu_{0}H_{\rm bias} = 1.5\;\hbox{mT}\) and \(I_{\rm id} = 4.4\;\hbox{A}\). The corresponding trapping frequency in each direction was calculated to be (ω x , ω y , ω z ) = 2π × (54, 280, 280) Hz, and Z trap was \(480\; \mu\hbox{m}\). We observed the signature of the BEC transition after 20 s evaporation. Figure 6 shows TOF images obtained after 15 ms, associated with optical density profiles obtained along the dotted line in the corresponding TOF images. We obtained the characteristic velocity distributions in the TOF images depending on the final radio frequency of the evaporative cooling ν f. In Fig. 6a, b, the broad velocity distribution indicates that the atomic gas remained in the thermal state at \(\nu_{\rm f}=1.770\; \hbox{MHz}\). The small asymmetric velocity distribution found in Fig. 6a was caused by the magnetic field of the remaining persistent supercurrent as explained in the previous section. In Fig. 6c, d, a bimodal velocity distribution was observed as the onset of the BEC transition at \(\nu_{\rm f}=1.750\;\hbox{MHz}\). The total number of atoms was estimated to be 1.5 × 105 by integrating over the absorption image, and the condensate fraction was about 40 %. From these results, we estimated the temperature of the atomic gas to be about 330 nK and the critical temperature of the BEC transition to be about 390 nK. When νf was decreased to 1.735 MHz, the thermal distribution was hardly observed and an almost pure condensate with a narrow velocity distribution was obtained as shown in Fig. 6e, f. Here, the number of condensed atoms was N = 3.4 × 104, and the peak density was \(2.5\times10^{14}\;\hbox{cm}^{-3}\).

Fig. 6
figure 6

TOF images after 15 ms and cross-sections of the optical density along the dotted line in the images. Each set of figures corresponds to the final radio frequency of evaporative cooling: a and b \(\nu_{\rm f}=1.770\;\hbox{MHz}\); c and d 1.750 MHz; e and f 1.735 MHz. The solid lines in (b, d, f) represent a Gaussian fitting to a thermal distribution and a Thomas–Fermi fitting to a condensate. The cross-sections clearly reveal the signature of the BEC transition: b a broad thermal distribution, d a bimodal distribution corresponding to a mixture of thermal gas and a condensate, and f a narrow distribution of an almost pure condensate. The field of view of each TOF image is \(490\;\upmu{\rm m} \times 490\;\upmu{\rm m}\)

Full size image

3.3 Decay measurement of condensates

The magnetic trapping potential produced on our persistent-supercurrent atom chip exhibited the very high stability and wide controllability. Next, we utilized these advantages to create BEC by systematically changing the trapping frequency. A highly stable magnetic potential is of great use in reducing the shot-to-shot fluctuations of the number of condensed atoms, so that we can measure the atom number decay precisely. For 87Rb, the dominant loss of the condensates is caused by the three-body recombination process [32,36]. This process is characterized by a three-body correlation function and can be used as a tool for elucidating the quantum statistical properties of atoms [37]. It is well known that the three-body loss rate of a BEC is 3! times smaller than that of thermal gas owing to the indistinguishability of condensed atoms. The measured decay rate provides us with further evidence of condensation.

For this purpose, we created three different magnetic trapping potentials by changing H bias with a fixed \(I_{\rm id} = 4.4\;\hbox{A}\). The corresponding trap frequencies were as follows: (i) \(2\pi\times(64,570,570)\;\hbox{Hz}\) at μ 0 H bias = 2.2 mT, (ii) \(2\pi\times(68,1050,1050)\;\hbox{Hz}\) at \(\mu_{0}H_{\rm bias}=3.2\;\hbox{mT}\), and (iii) \(2\pi\times(68,1320,1320)\;\hbox{Hz}\) at \(\mu_{0}H_{\rm bias}=3.7\;\hbox{mT}\). The change in μ 0 H bias in the range of about 1 mT widely modified the potential confinement in the yz-plane. We verified the production of an almost pure BEC without thermal fraction in each potential by TOF imaging. The cooling time was appropriately controlled according to the trapping frequencies: stronger confinement potential required shorter cooling time. For example, we employed about 7 s evaporative cooling for the strongest confinement potential. The decay measurement procedure is as follows. The produced BEC was confined in a magnetic trapping potential during holding time τ hold after the evaporative cooling was completed. The number of atoms remaining in the trap was then measured precisely from TOF images observed at 32 ms after release. We repeated this procedure at least 8 times for each holding time.

The symbols in Fig. 7 show experimental results for the number of remaining atoms N as a function of τ hold corresponding to the three different magnetic potentials mentioned above. The error in the measured data was mainly attributed to the difference in the initial number of atoms before evaporative cooling and the small signal-to-noise ratio in TOF images for smaller N. Figure 7 shows that atoms decayed more rapidly in a trapping potential with tighter confinement, which clearly indicates that the decay process strongly depended on the atomic density. In our experiment, the initial peak densities of condensed atoms trapped in the three different potentials were estimated to be (i) \((5.8\pm0.9)\times10^{14}\;\hbox{cm}^{-3}\), (ii) \((9.8\pm0.6)\times10^{14}\;\hbox{cm}^{-3}\), and (iii) \((1.2\pm0.1)\times10^{15}\;\hbox{cm}^{-3}\). Furthermore, each decay exhibits a nonexponential dependence on τ hold. These features seen in Fig. 7 cannot be simply explained by the single-body loss due to the background gas collisions. Three-body loss dominated the decay process of the trapped atoms we measured.

Fig. 7
figure 7

Number of remaining atoms N versus holding time τ hold. The filled circles [triangles, squares] and dashed [dotted, solid] line represent the experimental data and theoretical calculation with trapping frequencies of (i) \(2\pi \times(64, 570, 570)\;\hbox{Hz}\) [(ii) \(2\pi \times(68, 1050,1050)\;\hbox{Hz}\), (iii) \(2\pi \times(68, 1320,1320)\;\hbox{Hz}\)], respectively. The error bars represent the standard deviation of the measurements

Full size image

The lines in Fig. 7 represent N calculated by a numerical simulation. The simulation and measurement results are in good agreement. We expected the following simulation to capture the essential features of the decay process: all of the atoms were assumed to be a condensate in a three-dimensional trapping potential, and their indistinguishability was taken into account [37]; in addition, their densities were precisely determined with a variational method to solve the Gross–Pitaevskii equation [38, 39]. Note that, we calculated these three lines with only one variable H bias without any fitting parameters. We can thus conclude that the decay measurements reveal the systematic creations of BECs.

Let us remark the dimensionality of condensates in the present experiments. For the most elongated geometry (iii), an aspect ratio of the trapping frequencies ω y,z /ω x is about 20 (see Table 1). We can thus expect that the initial condensates with N ∼50,000 are prepared in the three-dimensional regime [40]. In the pioneering experimental studies, the one-dimensional systems have been realized with the aspect ratio of \(\gtrsim 200\) [22]. According to Ref. [40], for (iii), the system could begin to enter in the 3D-1D cross-over regime when N < 10,000, suggesting that a deviation between the experiments and the calculations for \(\tau_{\rm hold}\gtrsim 0.3\,{\text s}\) may be attributed to the beginning of the cross-over. Irrespectively, we can confirm the creation of the BEC in the three-dimensional system from the results at \(\tau_{\rm hold}\lesssim 0.2\;\hbox{s}\).

Table 1 Aspect ratio \(\omega_{y,z}/\omega_x\), atomic cloud sizes in the α-direction \(\ell_\alpha\; (\alpha=x, y, z)\), and interaction energies E int in units of \(\hbar\omega_{y, z}\), which were calculated for \(\mu_{0}H_{\rm bias}= 2.2, 3.2, \hbox{ and } 3.7\;\hbox{mT}\)
Full size table

3.4 Theoretical simulations

In what follows, we explain our method for calculating the decay process shown in Fig. 7. Furthermore, we present the simulation results in terms of atomic cloud size and the energy of the atoms. In particular, we discuss how the anisotropy of the trapping potential affects these quantities. We finally provide an estimation as regards the ability of our system to create quasi-one-dimensional systems.

We begin by overviewing the simulation. First, assuming all of the atoms to be a condensate, we determined the wavefunction of the condensate \({\varPsi}({\bf r})\) with the variational method detailed below. Next, we calculated certain quantities that characterize the atomic loss, such as the density of atoms \(N |{\varPsi}({\bf r})|^2\) and the three-body correlation defined as

$$g_3=\frac{N^3}{3!} \int \text{d}{\bf r}|{\varPsi}({\bf r})|^6,$$
(1)

where the factor 1/3! originates from the indistinguishability of condensed atoms. Finally, we examined the rate equation written as [32]

$$\frac{\partial N}{\partial \tau_{\rm hold}}= -\gamma_3 g_3 -\gamma_1 N,$$
(2)

where γ3 is the three-body loss rate, and γ1 is the single-body loss rate. For 87Rb in the \(|2,2\rangle\) state, γ3 has been determined as \(1.8\times10^{-29}\;\hbox{cm}^{-6}\hbox{s}^{-1}\), and in addition, the two-body loss has been found to be negligible [32]. We estimated the γ1 value to be \(1/65\;\hbox{s}^{-1}\) from the exponential decrease in N observed for a large \(\tau_{\rm hold} \gtrsim 30\;\hbox{s}\).

We detail the method for calculating \({\varPsi}({\bf r})\). It is well known that \({\varPsi}({\bf r})\) can be described by the Gross–Pitaevskii equation [38]:

$${\cal H}{\varPsi}({\bf r})=\mu {\varPsi}({\bf r}),$$
(3)

where μ is the chemical potential, and \({\cal H}\) is the mean-field Hamiltonian defined as

$${\cal H}= \sum\limits_{\alpha=x, y, z}\left( -\frac{\hbar^2 \boldsymbol{\nabla}_\alpha^2}{2M}+ \frac{M \omega_\alpha^2 \alpha^2}{2}\right)+ \frac{4\pi\hbar^2a_{\text{S}} N}{M} |{\varPsi}({\bf r})|^2,$$
(4)

where M is the mass of 87Rb atoms, and a S is the scattering length between two 87Rb atoms in the \(|2,2\rangle\) state, which is determined as 5.8 nm [32]. To solve Eq. (3), we used the variational method based on the expansion of oscillator eigenfunctions [39]. The variational function is given by

$${\varPsi}({\bf r})= \sum\limits_{\bf n} c_{\bf n}\psi_{\bf n}({\bf r}),$$
(5)

where ψ n (r) are the eigenfunctions of the harmonic oscillator with the quantum number n = (n x , n y , n z ), and the eigen-energies of ψ n (r) are given by \(E_{\bf n}=\sum\nolimits_{\alpha=x,y,z} \hbar \tilde{\omega}_\alpha ( n_\alpha + 1/2)\). We set the renormalized frequencies \(\tilde{\omega}_\alpha\) and the coefficients c n to be the variational parameters, and we determined \({\varPsi}({\bf r})\) by minimizing the energy E:

$$E=\int \text{d}{\bf r} \bigg( -\frac{\hbar^2 }{2M}\sum\limits_{\alpha=x, y, z}{\varPsi}^*({\bf r})\boldsymbol{\nabla}_\alpha^2{\varPsi}({\bf r}) + \frac{M}{2} \sum\limits_{\alpha=x, y, z}\omega_\alpha^2 \alpha^2 |{\varPsi}({\bf r})|^2 + \frac{2\pi\hbar^2a_{\text{S}} N}{M} |{\varPsi}({\bf r})|^4 \bigg).$$
(6)

Here, we limited n α to a maximum of 4 for simplicity, and we examined that the change in \({\varPsi}({\bf r})\) is small when n α further increases. Note that, our variational method effectively describes the broadening of wavefunctions caused by the repulsive interactions. Variational parameters \(\tilde{\omega}_\alpha\) can be rewritten as \(\hbar /(\tilde{a}_\alpha^2M)\), where \(\tilde{a}_\alpha\) characterize the widths of the renormalized wavefunctions, namely the variational principle \(\frac{\partial E}{\partial \tilde{\omega}_\alpha}=0\) yields smaller \(\tilde{\omega}_\alpha\) than the bare ω α for a positive scattering length a S , meaning that the width of the wavefunctions \(\tilde{a}_\alpha\) increases due to the broadening effects. This feature allows us to solve the Gross–Pitaevskii equations efficiently and with high precision even with small n α .

Focusing on the anisotropy of the trapping potential, we discuss the properties of the wavefunctions of the condensates. In Table 1, we first show the aspect ratio ω y, z /ω x for different \(\mu_{0}H_{\rm bias}=2.2, 3.2, \hbox{ and } 3.7\;\hbox{mT}\). The increase in H bias enhances the one-dimensional anisotropy: ω y and ω z greatly increase as H bias increases, while ω x remains almost the same.

Next, in Table 1, we present the atomic cloud sizes ℓ α with α = x, y, z, which were determined from the full widths at half maximum of \({\varPsi}({\bf r})\) in the α-direction. Note that ℓ α do not (necessarily) equal with \(\tilde{a}_\alpha\) unless n α is limited to 0. The atomic cloud broadens in the x-direction as H bias increases, while it shrinks in the y- and z-directions. This characteristic behavior results from the competing effects of the interaction and the anisotropic confinement: the interaction causes the broadening of the cloud, and the strong confinement suppresses it in the y- and z-directions; and thus, the cloud elongates in the x-direction.

We finally show the interaction energy E int calculated from the third term in Eq. (6). Comparing it with the trapping frequencies ω y, z , we further discuss the competition between the interaction and the anisotropy. Table 1 shows that E int and \(\hbar\omega_{y, z}\) are of the same order. Note that \(E_{\rm int}/\hbar\omega_{y, z} \ll 1\) is a criterion for achieving quasi-one-dimensional systems. The numerical simulation revealed that μ 0 H bias of about 10 mT yields \(E_{\rm int}/\hbar\omega_{y, z} \sim 1\), where ω x is about 2π × 50 Hz, and ω y, z are about 2π × 5 kHz. We thus expect that our system has the potential to provide one-dimensional systems. These estimations are consistent with those proposed in Ref. [40].

4 Summary

In this work, we have achieved a BEC on a persistent-supercurrent atom chip. An unknown misalignment of the bias magnetic field in our experimental setup required the following careful procedures for creating and controlling a magnetic trap. We compensated for the supercurrent additionally induced by the misaligned bias magnetic field. Furthermore, we measured two quantities related to the magnetic trap: the value of the potential minimum and the distance between the potential minimum and the chip surface. The precise direction of the bias magnetic field was finally determined by fitting the measurement results with the calculations based on the Biot-Savart law, allowing us to fully calculate the magnetic trapping potential. Experimentally, a persistent supercurrent in a closed circuit and a condensate both show very high sensitivity to a magnetic field. Therefore, the above procedures were essential to our achievement of a BEC using a superconducting atom chip with a closed-loop circuit.

The condensation was verified with two different measurements. We clearly observed the signature of a BEC transition in the TOF images, while the released atoms were slightly affected by the magnetic field originating from the persistent supercurrent. We next performed an atom number decay measurement to elucidate the indistinguishability of condensed atoms via three-body loss. The measured decay rates agreed quantitatively with the theoretical simulations, which assumed a pure condensate, and precisely dealt with the three-body loss process without any fitting parameters. In addition, we theoretically showed that a quasi-one-dimensional Bose gas is within our reach. It will be interesting future work to make atomic waveguides for quantum metrology or investigate many-body physics in low-dimensional systems for quantum simulations by taking full advantage of the highly stable magnetic trap produced on a persistent-supercurrent atom chip.