1 Introduction

Over the past decades, methods and techniques for controlling the velocity of pulse and realizing subluminal and superluminal light propagation in different media have become more and more attractive [1–5]. Subluminal and superluminal phenomena can be introduced in many applications including optical buffering, optical sensing [6–9], and optical phase array antenna [10]. In the early stage, the interest of research is often focused on the techniques using large normal or abnormal dispersion associated with an optical resonance. Electromagnetically induced transparency (EIT) and coherent population oscillations (CPO) are among the most prominent methods.

Other methods with distinguishing features of a broad range of operating wavelengths, operation at room temperature, and compatible with fiber-optic communication systems attract more researchers’ attention. Stimulated Brillouin scattering (SBS) [11–13], stimulated Raman scattering (SRS) [14], and Raman-assisted parametric process [15], which are associated with laser-induced amplifying resonant dispersion, have been extensively investigated to modulate the velocity of ultra-short pulse in optical fiber systems. However, the inherent limitations, such as narrow gain bandwidth (GHz) and relatively small temporal shift, constrain their performance in many optical communication systems.

It is also noticed that the group velocity control of femtosecond pulse has been demonstrated through χ 2 cascading interactions in quasi-phase-matched (QPM) gratings. Two kinds of schemes based on the different footholds for group velocity controlling, which are separately modulated by quadratic cascading nonlinearity [16], and transverse electro-optic effect [18] have been proposed. However, the interplay of group velocity modulation by quadratic and cubic nonlinearity is often ignored under the condition of intense femtosecond pulse input. In this paper, a method based on the combination of electro-optic effect and cubic nonlinearity is demonstrated to control the group velocity at room temperature in MgO-doped periodically poled lithium niobate (MgO:PPLN), where the group velocity of ultra-short pulses is modulated by adjusting the external DC electric field and controlling the intensity of input pulse under phase-mismatching conditions. The energy between the input pulse and converted pulse consequently exchanges back and forth along the propagation in the χ 2 cascading interactions. Compared with the schemes which control the group velocity by transverse electro-optic effect or quadratic cascading nonlinearity, the combination of electro-optic effect and cubic nonlinearity yields greater modulation. Therefore, we can control the group velocity of pulses in a broader range of modulation.

2 Theoretical model

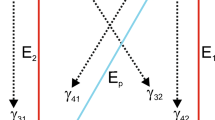
In our work, we consider the situation with femtosecond pulses incident onto a z-cut 5 mol% MgO:PPLN crystal along x direction (as shown in Fig. 1), and an external electric field applied along y direction. In MgO:PPLN, the transverse electro-optic effect induces the optical axis of each domain to alternately align at the angles of +θ and −θ with respect to the z axis which forms a kind of folded dielectric axis structure similar to that in a Solc filter [17]. The state of interest here is the energy coupling between ordinary wave (OW) and extraordinary wave (EW) in these folded domains under non-phase matching condition. The process about energy coupling in electro-optic effect under phase-mismatching condition, named as “polarization coupling cascading”, can be visualized as following steps: Taking account of OW incidence, the energy of OW flows to EW, but does not cause complete depletion; then the energy flows back from EW into OW due to phase mismatching. As a result, the OW is accelerated by the nonlinear phase shift brought from the inconsistence between the phase velocity of generated OW and original input OW.

Fig. 1
figure 1

Schematic of polarization coupling cascading process in MgO:PPLN crystal

Full size image

We derive the following coupled-mode equations for the polarization coupling, also taking the cubic nonlinear process into account, under the slowly varying envelope approximation to describe the interactions among the input pulse and the converted one inside the crystal:

$$ \frac{{\partial E_{1} }}{\partial Z} + \frac{{ik^{\prime\prime}_{1} }}{2} \cdot \frac{{\partial^{2} E_{1} }}{{\partial t^{2} }} = i\rho_{1} E_{2} \exp (i\varDelta k_{0} Z) + i\sigma_{1} [\left| {E_{1} } \right|^{2} E_{1} + 2\left| {E_{2} } \right|^{2} E_{1} ], $$
(1)
$$ \frac{{\partial E_{2} }}{\partial Z} + \delta \cdot \frac{{\partial E_{2} }}{\partial t} + \frac{{ik^{\prime\prime}_{2} }}{2} \cdot \frac{{\partial^{2} E_{2} }}{{\partial t^{2} }} = i( - \rho_{2} E_{1} \exp ( - i\varDelta k_{0} Z)) + i\sigma_{2} [\left| {E_{2} } \right|^{2} E_{2} + 2\left| {E_{1} } \right|^{2} E_{2} ], $$
(2)

where \( \rho_{i} (z) = \omega_{i} n_{1}^{2} n_{2}^{2} E_{y} \gamma_{51} /(c\sqrt {n_{1} n_{2} } ) \) (i = 1, 2, which denote the input pulse and the converted pulse) and σ i  = 3ω i χ 3/(8cn i ). E y denotes the transverse DC electric field, E i (z, t) denotes the amplitude of the electric field, and n 1, n 2 denote the refractive index of input and converted pulse, respectively. ω i denotes the angular frequency. Time t is measured in a time frame of the input pulse. k i is the wave vector of the central frequency, δ = k ′1  − k ′2 is the group velocity mismatching (GVM) between the input pulse and the converted pulse, where k ′ i is the inverse group velocity, and k ″ i  = d 2 k i /dω 2 is the group velocity dispersion (GVD), Δk 0 = k 2 − k 1 = 2π(n 2 − n 1)/λ 0 is the phase-mismatching vector, where λ 0 is the central wavelength of input pulse.

In this model, both self-phase modulation (SPM) and cross-phase modulation (XPM) are included, which is critical in considering the duration of ultra-short pulses in even moderate intensity.

3 Simulation results

The variables for the simulation are listed: The input OW duration is 70 fs centered at the wavelength of 1,550 nm, and the temperature is set to be 21 °C. The length of MgO:PPLN is set to be 20 mm, and the poling period is Λ = 19 μm. The value for χ 3of 5 mol% MgO:PPLN is set to be 1.03 × 10−22 m2/v2 which is calculated from its relationship with the nonlinear refractive index n 2. χ 3 = n 2 cn 20 /16π 2, [19] where n 2 = 9.7 × 10−11cm2/w [20]. Numerical simulation is carried out to solve Eq. (1) and Eq. (2) with a symmetric split-step beam-propagation method (BPM).

Figure 2 shows time advancement of the input OW and the generated EW. When OW passes through the sample, the polarization of OW is rotated by transverse electro-optic effect, so the pulse will propagate along the crystal at different velocity due to the non-QPM condition which results from the energy conversion between the OW and EW back and forth. Thus, the propagation time modulated by electro-optic effect is less than the propagation of no applying electric field. We can see that the time advancement of the output OW and the output EW reaches 90 and 82 fs, respectively, which is more than 1 times of the input pulse duration. Moreover, the OW pulse width only broadens to 94 fs due to the interplay of GVD and SPM/XPM.

Fig. 2
figure 2

Normalized pulse intensity of the interaction pulses with the electric-optic effect. Dashed line (solid line) represents the input (output) pulse intensity. Here, the input pulse is OW. The central wavelength of input pulse is 1,550 nm with the intensity of 20 GW/cm2, which corresponds to the GVM between OW and EW of 29 fs/mm. Both of the output pulses widths are 94 fs. In this case, the electric field is 3 kV/mm

Full size image

As shown in Fig. 3, the advancement and delay of output pulse can be obtained by changing the polarization of input pulse. When the input pulse is OW (EW), we achieve the result of the output OW (EW) acceleration (deceleration) case due to the negative (positive) GVM. Furthermore, it can be seen that both considerable advancement of 90 fs and delay of 94 fs are obtained.

Fig. 3
figure 3

Demonstration of the group velocity control with two different polarized incidence cases. Black dashed line represents the normalized intensity of temporal profile of input pulse. Red (Green) solid line refers to the advancement (delay) of OW (EW) incidence. The intensity of input pulse is 20 GW/cm2. In this case, the external electric field is 3 kV/mm

Full size image

Figure 4a–b shows the relationship between the advancement of OW (or delay of EW) and electric field, and Fig. 4c–d indicate its relationship with intensity of input pulse, respectively. From Fig. 4a–b, the result shows that time advancement (or delay) is almost in nonlinear proportion to the increasing electric field, so that it is possible to control the group velocity of the pulse by tuning the electric field. Another factor that gives an important impact on the delaying performance is the intensity of the injected pulses, where the numerical simulations are shown in Fig. 4c–d. By changing the intensity of input pulse from 10 to 60 GW/cm2, the change of time delay (or advancement) of output EW or OW is about 30 fs. We can conclude that the adjustment of intensity of input pulse is a effective approach to control the time delay (or advancement); however, we cannot use it blindly. The reshaping and distortion of output pulse induced by self- and cross-phase modulation cannot be ignored when the intensity of input pulse exceeds 56 GW/cm2, which is a critical point to the distorted output pulse.

Fig. 4
figure 4

Time advancement of OW or delay of EW vs. electric field and intensity of input pulse. a and c correspond to OW incidence, where the intensity of input pulse is 20 GW/cm2 for a, and the electric field is 3 kV/mm for c. b and d correspond to the case of EW incidence, where the intensity of input pulse for b, and the electric field for d are identical to case a and c

Full size image

Figure 5 shows the dependence of time delay of output pulse on electric field with different phase-mismatching condition. It should be noticed that under larger phase-mismatching condition, time delay will significantly decrease with the same electric field due to less energy exchange between OW and EW. The time delay (or advancement) of 50 fs can be obtained with modulating the electric field to 1.75 kV/mm under the condition of phase mismatching |Δk 1 L| = 86π, but the identical time delay (or advancement) is obtained by increasing the electric field to 2.75 kV/mm under the phase mismatching |Δk 2 L| = 109π. It can concluded that modulating the electric field with smaller phase mismatching is a flexible and efficient approach to control the group velocity of ultra-short pulse.

Fig. 5
figure 5

Time delay of output pulse as a function of electric field with different phase mismatching ΔkL. The purple and the pink curves refer to the poling period Λ 1 = 19 μm, which correspond to the phase mismatching |Δk 1 L| = 86π, whereas the cyan and the green curves refer to Λ 2 = 18.8 μm, corresponding to the phase mismatching |Δk 2 L| = 109π. The intensity of input pulse is set to be 20 GW/cm2

Full size image

Likewise, the time delay of output pulse versus the intensity of input pulse with different phase mismatching is calculated, and the corresponding curves are shown in Fig. 6. We adapt to the intensity of input pulse from 10 to 50 GW/cm2, the time delay (or advancement) which is corresponding to two different phase-mismatching conditions also rise. The effect is attributed to the nonlinear phase shift induced by cubic nonlinearity. Moreover, with larger phase mismatching, the change of the group velocity of input pulse is smaller than those with smaller phase mismatching. Because larger phase mismatching means less energy exchange between OW and EW, the influence on group velocity is weaker.

Fig. 6
figure 6

The dependence of time delay of output pulse on intensity of input pulse with different phase mismatching. The wine and the violet curves indicate to phase mismatching |Δk 1 L| = 86π, corresponding to the poling period Λ 1 = 19 μm. The dark yellow and the pink curves indicate to |Δk 2 L| = 109π, corresponding to Λ 2 = 18.8 μm. In this case, the electric field is 3 kV/mm

Full size image

4 Conclusion

In conclusion, we have demonstrated the ability of the quadratic and cubic cascaded nonlinear processes to perform the control of the group velocity of femtosecond pulses. Wider modulating range in group velocity is achieved through electric-optic effect rather than the intensity of input pulse. The significant advantage of our scheme is convenient to control the group velocity just by varying the electric field strength or the intensity of input pulse. Furthermore, larger phase-mismatching results in smaller time delay or advancement due to less energy exchange between OW and EW. Besides the approach of changing poling period, ways of changing the temperature and tuning injected central wavelength may also contribute to modulating the group velocity of pulse. It would be more flexible and sensitive if the scheme being utilized in waveguide system, and it will help us to practice in the future all-optical communications.