1 Introduction

High-repetition rate laser sources with few-cycle pulse durations and high-pulse energies are attractive for investigations of time-resolved photodynamic processes in atoms, molecules, clusters [1] and surfaces [2]. Such pulses are also utilized to generate spatially and temporally coherent extreme ultraviolet radiation through high-order harmonic generation, which have wide applications from attosecond physics [3] to surface electron dynamics [4]. Conventional approaches based on Ti:sapphire chirped-pulse amplification (CPA) laser systems require nonlinear spectral broadening processes in gas-filled hollow waveguides [5] or filamentation in gases [6] to reach the few-cycle regime in the visible. Due to its extremely broad working bandwidth and high single-pass gain, non-collinear optical parametric chirped-pulse amplification (OPCPA) presents a powerful alternative scheme, which allows a direct amplification of few-cycle laser pulses from an oscillator and shows negligible thermal problems [7]. Recently, a fiber pumped OPCPA system with 8-fs pulses at an average power up to 6.7 W, and a repetition rate of 96 kHz has been demonstrated [8], which has been further developed to generate sub-5-fs laser pulses with an average power of 3 W at a repetition rate of 30 kHz [9]. Sub-6-fs laser pulses with an average power of 430 mW at a repetition rate of 143 kHz have been generated and can be scaled to work at 500 kHz [10]. The OPCPA scheme allows to amplify oscillator pulses in the MHz regime. Less than two-cycle laser pulses with an average power of 22 W working at 1 MHz [11] have been achieved, and a sub-10-fs OPCPA system with an output power of 8 W at a repetition rate of 11.5 MHz [12] has been recently reported. For these systems, the temporal duration of the pump pulses were in the one picosecond range and the seed pulses were stretched to several hundred femtoseconds.

For pump pulses that have temporal durations of several tens or even more than hundred picoseconds, a corresponding temporal stretching of the seed pulses is required for improving the temporal overlap and to realize a reasonable conversion efficiency. Usually, a grating [13, 14] or grism [15, 16] stretcher is employed to achieve stretching ratios of 103–104. For a large stretching ratio, a careful dispersion management is important in order to properly recompress the pulses after amplification. A grism-pair stretcher has the advantage to provide both negative second and third-order dispersions. This allows to employ material dispersion in glass blocks with high transmission for the pulse compression. Theoretical calculations show that such kind of combination supports nearly an octave-spanning working bandwidth [17].

Here we present the design and realization of global dispersion management employing a grism-pair stretcher for down chirping the pulses, a material compressor, and an OPCPA system with a large stretching ratio of the seed pulses. We determine the residual dispersion after the compressor by the multi-photon inter-pulse interference phase scan (MIIPS) method [18]. Therefore, we introduce a visualization scheme of the MIIPS traces which enables an easy identification of the relevant higher-order dispersions, which are successively fed back to an acousto-optic programmable dispersive filter (AOPDF) for compensation. As a result, amplified pulses with a duration of 80 ps from 700 to 1,000 nm are recompressed by 350 mm SF57, 250 mm fused silica glass blocks, and the AOPDF to 9.6-fs-long pulses with low side lobes and an energy of 125 μJ at a repetition rate of 20 kHz.

2 Dispersion management

Long pump pulses of a few hundred picosecond duration can provide a high pump pulse energy to the amplifier at only moderate technical complexity, while maintaining good spatial and temporal beam profiles. To obtain a significant conversion efficiency, the seed pulse then has to be stretched to similar durations. This in turn requires a careful consideration of the dispersion compensation. In the following, these considerations are briefly reiterated for the present system before the MIIPS characterization of the pulses is discussed.

The dispersion of the whole system including the dispersions ϕ g(ω) resulting from the grism stretcher and ϕ m(ω) from all material in the OPCPA beam path including crystals, AOPDF and compressor glass can be written as

$$\varDelta \phi (\omega ) = \phi_{\text{m}} (\omega ) + \phi_{\text{g}} (\omega ) = \sum\limits_{k = 0}^{\infty } {\frac{{\varDelta \phi_{k} (\omega_{0} )}}{k!}(\omega - \omega_{0} )^{k} } ,$$
(1)

where Δϕ k (ω 0) is the kth-order dispersion at the central frequency ω 0. Δϕ 0 is a constant, and Δϕ 1(ω 0) is the group delay. Both of them have no influence on the pulse compression. Δϕ 2(ω 0) and Δϕ 3(ω 0) are the group delay dispersion (GDD), and the third-order dispersion (TOD), respectively. In a previous design [16], both Δϕ 2(ω 0) and Δϕ 3(ω 0) were set to zero to obtain matched second and third-order dispersions in the stretcher and compressor. This resulted in a flat dispersion around the central frequency, while the higher-order terms were left in the residual dispersion, imposing larger values to be compensated by an AOPDF.

However, such a lower-order flat dispersion is not a prerequisite for final pulse compression with an AOPDF. It has been shown that a broader spectral range can be compensated by a standard AOPDF when some lower-order dispersion is left [17]. The residual phase can be compensated if the residual spectral time delay is within the temporal working window \(\varDelta \tau_{0}\) of the AOPDF. Therefore, in the present design, we keep the time delay difference between the fastest frequency ω fast and slowest part ω slow of the pulse imposed by the residual dispersion within \(\varDelta \tau_{0}\), i.e.,

$$\varDelta \tau_{0} > \left| {\tau \left( {\omega_{\text{fast}} } \right) - \tau \left( {\omega_{\text{slow}} } \right)} \right|$$
(2)

In the calculation, the typical spectral range of an OPCPA pumped at 532 nm and seeded by a Ti:sapphire oscillator is considered [19]. Thereby, our present AOPDF limits the residual time delay spread to Δτ 0 < 3 ps. To simplify the alignment of the grism stretcher in the experiment, we fix the angle of incidence at the direction normal onto the surface of the first prism. The distance between the two apexes of the prisms is then varied to meet the requirements of Eq. (2). Other parameters such as the insertion amount at each prism and the distance between grating and prism are kept constant in the calculations as discussed in the previous work [16]. The materials include 250 mm fused silica, 25 mm TeO2 and 15 mm BBO. The length of SF57 is varied to achieve the optimal stretching ratio while maximizing the temporal overlap between pump and signal. The calculations show that up to 350 mm SF57 can be employed in the present design for the compressor, and the residual dispersion will still be kept in the working window of the AOPDF.

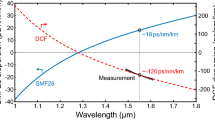
The results for the time delay and the residual dispersion are shown in Fig. 1a, b, respectively. A grism pair with 651 lines/mm generates a time delay of 80 ps from 689 to 1,011 nm at a central wavelength of 820 nm and provides more than 300 nm working spectral range (Fig. 1), in accordance with Dou et al. [17]. For comparison, Fig. 1b shows the residual dispersion obtained when the second and third-order dispersions are completely matched [16]. Due to a longer pathway through the material compressor, the working bandwidth is reduced from 230 nm for the previous design [16] to 206 nm, covering the spectral range from 737 to 943 nm at the central wavelength of 820 nm. The results show that the present design provides with Δλ ~ 320 nm, a significantly larger working bandwidth from 689 to 1,011 nm. A polynomial fitting of the residual dispersion up to fifth order is also shown as open dots in the Fig. 1b. The good agreement between the theoretical calculation and the polynomial fitting indicates that the residual dispersion has a regular distribution and can be described well by the first five terms of Eq. (1).

Fig. 1
figure 1

a The dependence of the spectral time delay for grisms with 651 and 300 lines/mm. Black solid lines dispersion of the material, blue dotted lines grism dispersion designed in [16] and red dashed lines grism dispersion of the present design. The sign of the grism dispersions are reversed for convenience. b Comparison of the residual time delay for different designs for the grisms with 651 lines/mm. The blue solid line denotes the previous design [16], the red line present results, and the dots denote a polynomial fitting of the residual time delay

Full size image

When different apex angles of the prisms in the grisms are chosen, the working spectral range can be shifted and thus adapted to the desired spectral range, as shown in Fig. 2a. For apex angles of α = 22.3°, 22.5° and 22.7°, the spectral bandwidths cover the ranges from 674 to 996 nm (Δλ ~ 322 nm, green dashed line), from 689 to 1,011 nm (Δλ ~ 322 nm, red solid line), and from 698 to 1,034 nm (Δλ ~ 326 nm, blue dots), respectively. For the present OPCPA system, an apex angle of α = 22.5° is chosen.

Fig. 2
figure 2

a Dependence of the residual time delay for grisms with different apex angles α and a grating with 651 lines/mm. b Dependence of the residual time delay on the incident angle θ onto the grism for θ = −0.2° (green dashed), 0.0° (red solid) and +0.2° (blue dots) and a grating with 651 lines/mm

Full size image

The sensitivity of the residual dispersion on the incident angle θ for a given prism with α = 22.5° is shown in Fig. 2b. A negative shift of the incidence angle by Δθ = −0.2° increases considerably the residual dispersion beyond the working range of the AOPDF, which results in uncompensated parts in the pulses. To the contrary, a positive shift of the incidence angle by Δθ = +0.2° reduces the residual dispersion, but on the expense of a narrower bandwidth. These results show that such a shift of the incidence angle is sufficient to alter the performance of the system, which indicates that in practice a careful alignment of the grism pair is required.

When a grating with 300 lines/mm is used, the apex angle of the grism is optimized to α = 18.8° for a similar spectral working range. The corresponding time delay introduced by the grism pair is further extended to Δt ~ 160 ps in the same spectral range, as shown in Fig. 1a. This stretching is about twice as large as obtained with the grating with 651 lines/mm. For longer pump pulses, a correspondingly better temporal overlap between pump and seed is obtained with possibly larger conversion efficiency. This longer stretching requires a beam path of about 750 mm through SF57 in the compressor. The residual time delay after the compressor is shown in Fig. 3. It provides a much larger spectral bandwidth than the results obtained with the earlier design [16].

Fig. 3
figure 3

Comparison of the residual time delay for different designs for grisms with 300 lines/mm. The blue solid line denotes the previous design [16], the red line the present results, and the dots denote a polynomial fitting of the residual time delay

Full size image

Table 1 shows the residual dispersions fitted with a polynomial function up to fifth order for both grism stretchers. The fitting results are also shown as dotted lines in Figs. 1b and 3. In comparison with the previous results [16], now a certain amount of GDD and TOD is kept in the present design, which partly balances the higher-order dispersions and leads to a significant extension of the working bandwidth. Table 1 also indicates that the experimental setup of the grism stretcher is much more compact when using the 651 l/mm grating compared the 300 l/mm one.

Table 1 Residual dispersions
Full size table

3 Residual dispersion compensation with MIIPS

A great amount of residual dispersion is still kept in the amplified pulses after the material compressor as is shown above. For further compensation by the AOPDF, this dispersion has to be detected. Frequency-resolved optical gating (FROG) [20] and spectral phase interference for direct electric field reconstruction (SPIDER) [21] have been widely implemented to characterize ultrashort laser pulses. However, in order to meet the requirement of the Shannon sampling theorem in FROG, a huge amount of data has to be collected to retrieve the spectral phase information for compression to few-cycle pulses with a large time-bandwidth product. Due to the complicated iterative mathematical algorithm for the phase retrieval, this will be time-consuming. The SPIDER technique can achieve the spectral phase information much faster, but the retrieval algorithm has to be corrected when it is used to characterize strongly chirped pulses [22]. Furthermore, it will be somewhat problematic or difficult to retrieve the phase information from the shearing spectral fringe if the pulse spectrum shows a complex structure or other parasitic components [10]. In contrast to both techniques, the multi-photon intrapulse interference phase scan (MIIPS) [18] is a single-beam technique to characterize ultrashort pulses with the help of an active pulse shaper which has attracted attention recently due to its much simpler setup and easier operation. Particularly, when a pulse shaper is already incorporated in the system, only a nonlinear crystal and a spectrometer are required additionally, and influences of further optical components on the pulse measurement can be avoided. In the following, we will focus on this method and show how to visually detect and correct the large amount of residual higher-order dispersion in the pulses.

The ultrashort pulses can be expressed in the frequency domain as

$$\tilde{E}(\omega ) = A(\omega )\exp \left[ { - i\phi (\omega )} \right],$$
(3)

where, A(ω) denotes the amplitude and ϕ(ω) the spectral phase.

The electric field of second harmonic generation (SHG) at frequency Ω = 2ω of the ultrashort pulses described by Eq. (3) is given by

$$\tilde{E}_{\text{SHG}} (\varOmega ) = \int {A(\omega - \varDelta \omega )A(\omega + \varDelta \omega )\exp \left[ { - i\varDelta \phi (\omega ,\varDelta \omega )} \right]{\text{d}}\varDelta \omega } .$$
(4)

The phase term in Eq. (4) is

$$\begin{aligned} \varDelta \phi (\omega ,\varDelta \omega ) & = \sum\limits_{k = 0}^{\infty } {\frac{{\phi^{(k)} (\omega )}}{k!}(\varDelta \omega )^{k} + } \sum\limits_{k = 0}^{\infty } {\frac{{\phi^{(k)} (\omega )}}{k!}( - \varDelta \omega )^{k} } \\ & = 2\phi_{0} + \phi^{(2)} (\omega )(\varDelta \omega )^{2} + O\left( {\varDelta \omega^{4} } \right). \\ \end{aligned}$$
(5)

If the spectral phase varies smoothly enough in the whole spectral range, only the second term in Eq. (5) contributes dominantly to SHG. Inserting Eq. (5) into Eq. (4) and neglecting the higher-order \(\varDelta \omega^{4}\) terms, the maximal SHG signal is obtained when the argument in the exponential term is zero, i.e.,

$$\phi^{(2)} (\omega ) = 0$$
(6)

If a known second-order dispersion f (2)(ω) is added to the pulse, the above condition is modified to

$$\phi^{(2)} (\omega ) + f^{(2)} (\omega ) = 0$$
(7)

Since the added GDD f (2)(ω) is known, the unknown GDD in the pulses ϕ (2)(ω) can be derived from the frequency position where the scanning function f (2)(ω) maximizes the SHG intensity, which is the basic principle of MIIPS [18].

When a sinusoidal scanning function \(f(\omega ,\delta ) = \alpha \sin [\gamma (\omega - \omega_{0} ) - \delta ]\) is applied, the GDD at the frequency ω in the pulse can be derived from the second derivative of f(ω, δ) as

$$\phi^{(2)} = \alpha \gamma^{2} \sin \left[ {\gamma (\omega - \omega_{0} ) - \delta } \right]$$
(8)

Here α is a parameter to determine the GDD scanning range, γ is a constant related to the spectral bandwidth of the pulses and generally is set to be the transform-limit pulse duration, and δ denotes the scanning variable to alter the GDD value of the scanning function. Equation (8) indicates that the maximum GDD value which can be detected amounts to αγ 2. When the absolute value of ϕ (2)(ω) is larger than αγ 2, the intensity distribution of SHG becomes irregular during scanning and the spectral phase cannot be detected correctly with the algorithm based on the detection of the peak position [18].

The relationship between the scanning variable δ and the spectral angular frequency ω is derived from Eq. (8),

$$\delta = n\pi + \gamma (\omega - \omega_{0} ) + ( - 1)^{n + 1} \arcsin \left[ {\frac{{\phi^{(2)} (\omega )}}{{\alpha \gamma^{2} }}} \right],\quad n\;{\text{integer}}.$$
(9)

The spectral phase ϕ(ω) can be expanded in a Taylor series at the central frequency ω 0 as,

$$\phi (\omega ) = \phi_{0} (\omega_{0} ) + \sum\limits_{k = 1}^{\infty } {\frac{{\phi_{k} (\omega_{0} )}}{k!}(\omega - \omega_{0} )^{k} } ,$$
(10)

and the corresponding ϕ (2)(ω)is

$$\phi^{(2)} (\omega ) = \sum\limits_{k = 2}^{\infty } {\frac{{\phi_{k} (\omega_{0} )}}{(k - 2)!}} \left( {\omega - \omega_{0} } \right)^{(k - 2)} ,$$
(11)

where ϕ k (ω 0) is the kth-order dispersion at ω 0.

Equation (9) can be further approximated if the condition \(\phi^{(2)} (\omega ) < < \alpha \gamma^{2}\) is valid,

$$\delta = n\pi + \gamma (\omega - \omega_{0} ) + \frac{{( - 1)^{n + 1} }}{{\alpha \gamma^{2} }}\left\{ {\sum\limits_{k = 2}^{\infty } {\frac{{\varDelta \phi_{k} (\omega_{0} )}}{(k - 2)!}(\omega - \omega_{0} )^{k - 2} } } \right\},\quad n\;{\text{integer}}.$$
(12)

With this analytical expression, the dependence of the MIIPS trace on each dispersion order near the central frequency ω 0 can be analyzed, which is outlined in the following.

3.1 Transform-limited pulses

If the pulse has no dispersion, Eq. (12) can be simplified to

$$\delta = n\pi + \gamma (\omega - \omega_{0} ).$$
(13)

Equation (13) shows that the scanning variable δ depends linearly on the angular frequency ω with a slope of γ. The MIIPS traces will be exactly distributed along theses parallel lines with a separation of π due to its modulo π dependence.

Figure 4 shows simulated MIIPS traces where Ω is shown as a function of scanning variable δ. The parallel lines (PLn, n = 0, 1, 2, 3) shown by Eq. (13) indicate that those lines are actually the theoretical expectations for pulses without any dispersion and their positions only depend on the scanning parameters. Another horizontal line at Ω = 2ω 0 is further added in the figure; it will be shown that both the parallel and the horizontal lines can be used to judge the spectral dispersion of the pulses visually.

Fig. 4
figure 4

MIIPS trace for transform-limited pulses

Full size image

3.2 Group delay dispersion

If the pulse shows only GDD, the relationship in Eq. (12) can be expressed as

$$\delta = n\pi + \gamma (\omega - \omega_{0} ) + ( - 1)^{n + 1} \frac{{\phi_{2} (\omega_{0} )}}{{\alpha \gamma^{2} }}.$$
(14)

It shows that the MIIPS traces are still parallel to each other again with a constant slope of γ, but the distance between two adjacent traces is no longer equal. The amount the trace is shifted with respect to the transform-limited trace depends on the ratio of the GDD to the maximum scanning value αγ 2, while the direction of the shift depends on the sign of the GDD. As shown in Fig. 5, when the GDD is negative, the traces shift to the right of the PLn for even n in Eq. (14), and to the left when n is odd. For GDD > 0, it is vice versa. The dashed lines indicate the traces expected for transform-limited pulses.

Fig. 5
figure 5

MIIPS trace for constant GDD. In the simulation α is set to α = 2π, γ = 8 fs, GDD is −200 fs2 for a and 200 fs2 for b

Full size image

3.3 Third-order term of the spectral dispersion

For third-order dispersion, only Eq. (12) yields in this case

$$\delta = n\pi + \gamma (\omega - \omega_{0} ) + ( - 1)^{n + 1} \frac{{\phi_{3} (\omega_{0} )}}{{\alpha \gamma^{2} }}(\omega - \omega_{0} ).$$
(15)

The equation shows that the TOD will change the slope of the traces such that the traces will be tilted against the parallel lines, with different slopes for consecutive traces. If the TOD is negative, they tilt clockwise for even n and counterclockwise for odd n. The behavior will be reversed when the TOD is positive, as illustrated in Fig. 6. The traces cross through the parallel lines at the intersection points of the parallels lines and the horizontal line. Along the horizontal line Ω = 2ω 0, the trace distance between adjacent traces is again π.

Fig. 6
figure 6

MIIPS trace for constant TOD. In the simulation α = 2π, γ = 8 fs, TOD is −1,000 fs3 for a and 1,000 fs3 for b

Full size image

3.4 Fourth-order term of the spectral dispersion

If only the fourth-order term contributes to the spectral dispersion, the relationship between δ and ω can be written as

$$\delta = n\pi + \gamma (\omega - \omega_{0} ) + ( - 1)^{n + 1} \frac{{\phi_{4} (\omega_{0} )}}{{\alpha \gamma^{2} }}(\omega - \omega_{0} )^{2} .$$
(16)

The traces are now parabolic curves centered at the intersection of the horizontal line Ω = 2ω 0 with the PLn lines. For adjacent traces, the direction of the curvature is opposite. If the FOD is negative, the traces will be curved to the right of the PLn for even n and to the left for odd n. The behavior is just opposite when the FOD is positive, see Fig. 7. In comparison with the TOD, the traces are now located only on one side of the parallel lines and do not cross them. This enables an easy distinction between TOD and FOD. Again, the trace distance at the horizontal line Ω = 2ω 0 is π.

Fig. 7
figure 7

MIIPS trace for constant FOD. In the simulation α = 2π, γ = 8 fs, FOD is −1×104 fs4 for a and 1 × 104 fs4 for b

Full size image

3.5 Fifth-order term in the spectral dispersion

If only the fifth-order term contributes to the spectral dispersion, the relationship between δ and ω can be written as

$$\delta = n\pi + \gamma (\omega - \omega_{0} ) + ( - 1)^{n + 1} \frac{{\phi_{5} (\omega_{0} )}}{{\alpha \gamma^{2} }}(\omega - \omega_{0} )^{3} .$$
(17)

Figure 8 shows that the MIIPS traces have a “S”-like shape when the pulse has only fifth-order dispersion. The traces for even higher-order dispersion can be analyzed in a similar way.

Fig. 8
figure 8

MIIPS trace for constant FiOD. In the simulation α = 2π, γ = 8 fs, FiOD is −2×105 fs5 for a and 2 × 105 fs5 for b

Full size image

Generally, for odd-order dispersions, the traces cross through the intersection points of the parallel zero dispersion lines and the horizontal line Ω = 2ω 0, while for the even-order dispersions the traces are located on one side of the zero dispersion lines. The analysis shows that the trace positions δ along horizontal line Ω = 2ω 0 depend only on the amount of GDD at the central frequency ω 0. Therefore, from this information, the GDD at the central frequency can unambiguously be determined.

It should be pointed out that the above analysis is carried out under the approximation that the pulse dispersion ϕ (2)(ω) is much less than the maximum amount of the scanning function αγ 2. This implies that the trace properties can only be visualized in the vicinity of the central frequency where this approximation is valid.

If the scanning range αγ 2 is limited by the performance of the AOPDF, it will be problematic for a correct detection of the spectral phase that goes beyond this range. In this case, the algorithm based on the detection of the SHG peak position in MIIPS is still valid near the central frequency ω 0 at each order. Once the spectral phase of the central frequency ω 0 is determined, it can be easily extended to the whole spectral range with a polynomial fitting. Therefore, it is quite helpful when the residual dispersion can be described with finite terms in a Taylor expansion as shown in Fig. 2.

4 Experimental results

The above analysis of the residual higher-order dispersion has been tested in an OPCPA system with down-chirped stretching. For this purpose, a compact grism-pair stretcher with a footprint of 17.5 × 17.5 cm2 is built as shown in Fig. 9. Gratings with 651 lines/mm (Carl Zeiss Microimaging) and AR-coated SF57 prisms (Hellma Optik) with an apex angle of α = 22.5° are used in the grism-pair stretcher. The transmission efficiency of the stretcher is measured to be 30 %. The stretcher is implemented in a two-stage three-pass OPCPA system. Pump pulses of 200 ps duration, 1.3 mJ energy at λ = 532 nm and a repetition rate of 20 kHz are employed [23, 24]. The sub-6-fs seed (Femtolaser, Rainbow) is down-chirped to 80 ps from about 700 to 1,000 nm and amplified to a pulse energy of about 140 μJ with a spectrum supporting a transform-limit pulse duration of 8.1 fs. The amplified pulses are compressed with 350 mm Brewster-cut SF57 and 250 mm fused silica glass blocks with a total transmission of 90 %, thus yielding an output pulse energy of 125 μJ at a repetition rate of 20 kHz. A quantum efficiency of about 15 % was thus achieved.

Fig. 9
figure 9

The compact grism-pair stretcher implemented in the experiment

Full size image

A coarse compression is carried out without AOPDF and is checked by an intensity autocorrelation measurement (IAC). Figure 10a shows the pulse duration in dependence of the change of the beam path in a SF57 glass block. The shortest pulse duration is 15.9 fs with the assumption of a Lorentzian temporal profile. However, a long tail spanning a 1.4 ps range in the IAC as shown in Fig. 10b indicates uncompensated high-order dispersions, especially the fourth-order dispersion, in the pulses.

Fig. 10
figure 10

Pulse compression with material only: a pulse duration in dependence of SF57 material change, the shortest pulse duration is about 16 fs. b A full scan of an IAC reveals a long pulse tail in the 1.4 ps range

Full size image

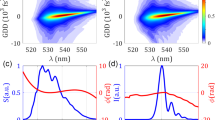
The residual spectral phase is detected with MIIPS as discussed above and compensated with an AOPDF (Fastlite, Dazzler). For the MIIPS characterization, a type-I phase-matched BBO crystal with 20-μm thickness is utilized together with a fiber coupled UV spectrometer (Avaspec 3648-USB2 330–573 nm). Figure 11 shows the MIIPS measurement while compensating the dispersion. In Fig. 11a, the MIIPS traces are shown without residual dispersion compensation. For the MIIPS analysis, the parameters in the scanning function δ are set to α = 8π and to γ = 8 fs. Clearly, contributions mainly from TOD and FOD are directly observed; the second-order dispersion is practically not present, because the MIIPS traces intersect at the central wavelength, the crossing between the parallel lines PLn and the horizontal line. The strongly curved traces indicate a strong negative FOD within the pulses, which agrees with the long tail observed in the intensity autocorrelation (Fig. 10b).

Fig. 11
figure 11

MIIPS traces a without any compensation, and after partial compensation of b FOD, c TOD, and d again TOD at smaller α parameter α = 3π and therefore higher phase sensitivity

Full size image

After partly compensating the FOD, clockwise tilted MIIPS traces at odd PLn orders are obtained as shown in Fig. 11b. This indicates that now a positive TOD is dominant in the actual pulses. Figure 11c shows the result when the TOD is compensated. In comparison with Fig. 11a, the MIIPS traces are approaching the zero dispersion lines but are still weakly curved. To further compensate the higher-order dispersion, α is set to α = 3π in order to improve the phase detection sensitivity, see Fig. 11d. The final result after a careful compensation following the above steps is shown in Fig. 12a. The MIIPS traces now nearly coincide with the zero dispersion lines; however, some subtle structures exist at both spectral ends. This indicates the presence of FiOD. The experimental TOD and FOD agree within 20 % with the expected calculated values. Only part (about 25 %) of FiOD could be compensated (the traces are not shown) in the experiment, because the diffraction efficiency of AOPDF decreases rapidly when larger values of FiOD dispersion are loaded which leads to an inefficient diffraction.

Fig. 12
figure 12

a MIIPS traces for the compensated pulses. b Fringe-resolved autocorrelation of the compressed pulses (dots: measurement, solid: retrieved)

Full size image

The final temporal pulse shape is characterized with a dispersion-balanced fringe-resolved autocorrelator (FRAC) and the results are presented in Fig. 12. A measurement over a large scan range indicates no significant intensity outside of the plotted ±50 fs temporal window.

The spectral phase is retrieved with the PICASO algorithm [25], and the temporal electric field is re-built based on the retrieval results, as shown in Fig. 13. The results show that part of the fifth-order dispersion still remains in the compressed pulses particularly at longer wavelengths. The reconstructed temporal intensity profile indicates a pulse duration of Δτ ~ 9.6 fs (FWHM) with only low side lobes of about 3 and 9 % of the peak intensity preceding and trailing of the main pulse, respectively. With these retrieved data, the numerically simulated FRAC trace is also presented in Fig. 12b (solid line). A good agreement between experimental measurement and theoretical simulation is achieved.

Fig. 13
figure 13

Amplified signal pulse after compression: a the measured signal spectrum (red) and the retrieved spectral phase (blue), and b the reconstructed temporal intensity envelope (red) and its phase (blue)

Full size image

5 Conclusion

In summary, we have designed a grism-pair stretcher to considerably extend the working spectral range. The setup has successfully implemented in a two-stage three-pass non-collinear OPCPA system. The seed is down-chirped to 80 ps from about 700 to 1,000 nm and re-compressed with a material compressor. The residual phase of the broadband spectrum is easily visualized using the MIIPS method. From the MIIPS traces, the individual higher-order dispersions are retrieved and fed back to the AOPDF for final compensation, yielding pulses with a temporal duration of 9.6 fs (FWHM) with only weak pre- and post-pulses. Therefore, a grism stretcher and material compressor together with the residual phase visualization by MIIPS enables the operation of OPCPA systems with long pump pulses. For such systems, fluctuations in the synchronization of pump and seed pulses are not important. For a complete compensation of FiOD, a longer crystal in the AOPDF or less dispersive compressor material is desirable. Although parametric amplification by pump pulses with a duration in the low picosecond range is optically easier to realize, the complexity of such systems which require an optical synchronization between pump and seed pulses is considerably higher.