Theory and simulation of ion Coulomb crystal formation in a Penning trap

Abstract

Ion Coulomb crystals (ICCs) are formed by laser-cooled ions in both radio-frequency and Penning traps. In radio-frequency traps, the crystals are generally stationary. In Penning traps, ICCs always rotate. The frequency of rotation is often set by an applied rotating wall drive that forces the crystal to rotate at the same frequency as the drive. In the absence of any applied rotating or oscillating fields, ICCs in a Penning trap can be in stable equilibrium with a range of rotation frequencies. The density and shape of the crystal adjust with the rotation frequency to ensure that equilibrium is reached. Here, we show that the parameters of the radial laser-cooling beam determine the rotation frequency of a small crystal in a Penning trap when no driving fields are present. We demonstrate, using an approximate theoretical treatment and realistic simulations, that the crystal rotation frequency is independent of the number of ions and the trap parameters, so long as the crystal radius remains smaller than the cooling laser beam waist. As the rotation frequency increases, the crystal eventually becomes a linear string, at which point it is no longer able to adjust its density. Instead, a small amplitude vibration in the zigzag mode of oscillation manifests itself as a rotation of the crystal at a fixed frequency that depends only on the applied trap potential.

1 Introduction

Atomic ions trapped in radio-frequency (RF) and Penning traps are remarkable systems that can be used for a wide variety of experiments in areas such as spectroscopy, fundamental physics, quantum information processing, precision measurements and plasma physics [1,2]. Some of these experiments use single ions, some use small numbers of particles and some use large clouds containing many thousands of ions.

One particular aspect of experiments with more than one ion in a trap is the possibility of the formation of an ion Coulomb crystal (ICC). This is a state of the system where the ions take up fixed positions relative to each other. With large numbers of ions, this becomes a regular lattice structure that is very similar to a condensed matter crystal. The main difference is that the inter-ion spacing is much greater than that in a conventional crystal, being typically 10 μm. The number density of such ion crystals is therefore typically of the order of 10¹² times lower than that of a conventional atomic crystal. The interaction between the ions is completely dominated by the Coulomb interaction at these large distances, and for a single-species ICC, the atomic structure of the particles plays no role in determining the crystal structure.

Many experiments with laser-cooled trapped ions have demonstrated the formation of ICCs when the temperature of the ions is low enough. Studies have been carried out in RF traps (see for example, [3–5]) and also in Penning traps [6]. The onset of crystal formation is governed by the value of the Coulomb-coupling constant, $\varGamma$, which is given by

$$\varGamma=e^2/4\pi\epsilon_0ak_BT.$$

(1)

Here, the Wigner–Seitz radius a is defined through (4/3)π a ³₀ n ₀ = 1 where n ₀ is the number density of ions. For an infinite plasma, simulations show that a first-order liquid–solid phase transition takes place at $\varGamma\approx 170$ [7, 8].

Ion Coulomb crystals (ICCs) can take many forms, from a simple one-dimensional string of ions along the axis of a trap to a solid three-dimensional structure. Different configurations of crystals are suited to different applications. For example, strings of ions in a linear radio-frequency trap have been used in quantum information studies (e.g. [9]). The transition from a linear string to a zigzag structure has been applied to a study of the Kibble–Zurek mechanism concerning the formation of defects in phase transitions [10–12]. Three-dimensional crystals have been used for the study of reaction rates between ions and neutral molecules [13]. In a Penning trap, unlike in radio-frequency traps, the crystal always rotates (see Sect. 4), but for many experiments this does not cause problems. The structure of a three-dimensional crystal in a Penning trap has been investigated by the use of Bragg scattering [14] and two-dimensional planar crystals have been used to simulate the interaction of spins [15].

In this article, we will be concerned with the formation of ICCs with small numbers of ions (less than approximately 20 ions) in Penning traps. We first review the trapping mechanism in a Penning trap (Sect. 2) and then we introduce a simple theoretical model for laser cooling of ions in this system (Sect. 3). In Sect. 4, we apply these results to the formation and configuration of ICCs in the Penning trap, and in Sect. 5, we discuss simulations that confirm the analysis provided in Sect. 3 and 4. Our conclusions are presented in Sect. 6.

2 The Penning trap

2.1 Motion of a trapped ion

The Penning trap confines charged particles (here atomic ions) by the use of static electric and magnetic fields [1]. Electrodes are designed to give a potential that has cylindrical symmetry and a purely quadratic dependence on position close to the centre of the trap, given by

$$\phi(r,z)=A(2z^2-r^2).$$

(2)

The required potential is most straightforwardly generated using three electrodes that follow the equipotential curves corresponding to Eq. 2. Alternatively, the potential can also be generated using a stack of hollow cylindrical electrodes with dimensions chosen to minimise the higher-order terms in the potential (in particular the quartic term, as all odd-powered terms should be absent for electrode structures having reflection symmetry about the trap centre).

The electrostatic potential confines positively charged particles in the axial direction if A is positive. The potential then has a minimum along the axial (z) direction. However, this causes the potential to have a maximum in the radial (r) direction, so the motion is unstable in this plane. Loss of particles from the trap can be avoided if a static magnetic field (with magnitude B) is applied along the z direction. The Lorentz force on the particles (having charge e and mass m) arises from both the electric and magnetic fields, and solution of the resulting equations of motion shows that the motion of a single ion has three components: an axial oscillation at an angular frequency ω _z , a modified cyclotron orbit in the radial plane at ω _c and a slower magnetron orbit in the radial plane at ω _m . These angular frequencies are defined by:

$$\omega_z=(4eA/m)^{1/2}$$

(3)

$$\omega_c=\varOmega/2+\omega_1$$

(4)

$$\omega_m=\varOmega/2-\omega_1$$

(5)

where

$$\omega_1=(\varOmega^2/4-\omega_z^2/2)^{1/2}$$

(6)

and the pure cyclotron frequency is given by $\varOmega=eB/m$.

2.2 The rotating frame

In order to discuss some aspects of the motion of ions in the Penning trap, it is convenient to move into a frame that rotates at half the cyclotron frequency, i.e. at $\varOmega/2$ [16]. In this frame (which we will refer to as the frame R), the Coriolis force arising from the rotation exactly balances the force on the particles due to their motion in the magnetic field, so the force on an ion now has no contribution that depends on its velocity. However, the radial potential is also modified due to the rotation (i.e. as a result of the centrifugal force) and acquires a positive quadratic term proportional to $\varOmega^2/4$ that dominates over the negative electrostatic term. The end result is an effective radial confining potential corresponding to the angular frequency ω ₁ defined above. Therefore, the parameter ω ₁ that emerges from the equations of motion has a clear physical interpretation as the harmonic oscillation frequency in the radial potential well in the rotating frame R.

Within the rotating frame R, the orbit of a single ion in one sense (+ω ₁) corresponds to the cyclotron motion (when transformed back into the laboratory frame) while an orbit in the opposite sense (−ω ₁) corresponds to the magnetron motion. In general, the motion in the rotating frame is elliptical and corresponds to an epicyclic superposition of the cyclotron and magnetron motions in the laboratory frame.

The trap becomes unstable when the axial confinement is raised above a critical value at which ω ₁ becomes zero. This corresponds to a flat effective potential in the rotating frame, leading to loss of radial confinement.

3 Laser cooling in the Penning trap

3.1 Laser cooling of a single particle

Doppler laser cooling utilises the radiation pressure from a laser beam interacting resonantly with atomic particles to slow them down. The Doppler effect is used to bring the laser frequency in and out of resonance depending on the velocity of the particle: if the laser is tuned slightly to the lower-frequency side of the transition, the scattering rate is higher when the particle is moving towards the laser. The equilibrium temperature of the ion is set by the balance between this cooling process and heating arising from the recoil of the particle from re-emission of photons, which is in a random direction.

Doppler cooling works very effectively in radio-frequency ion traps. It can also be applied to an ion trapped in a Penning trap, but it is complicated by the fact that the magnetron motion has a negative total energy. Here, we define “cooling” as a reduction of the size of the orbit, so for the magnetron motion this actually corresponds to an increase in total energy (though still a reduction in kinetic energy). For a laser-cooling beam that passes through the centre of the trap radially, the cyclotron motion is cooled, but the magnetron motion is heated, so the ion will be lost. It has been shown that in order to cool the ion effectively with a radial laser beam (a situation often referred to as “perpendicular laser cooling"), it is necessary to offset the beam so that there is a gradient of laser intensity across the centre of the trap. This can be shown in a number of different ways. Itano and Wineland [17] were the first to treat the problem in detail, starting from the change in velocity arising from individual photons scattering from the ion. Later, Thompson and Papadimitriou carried out a complementary analysis treating the system as a damped simple harmonic oscillator [18] but leading to the same criterion for successful cooling. Here, we summarise this model briefly and in Sect. 4, we extend the analysis to the situation where several ions are trapped in a small Coulomb crystal.

3.2 Theoretical model

The Doppler cooling limit for a trapped ion (depending on the details of the trap and the laser-cooling parameters) is typically 0.5 mK [17]. We will treat the case of Ca⁺ here but the results are similar for other species. The Doppler limit for typical Penning trap parameters corresponds to motion with an rms amplitude of the order of 1 μm and a velocity amplitude of the order of 1 m s⁻¹ (giving a Doppler shift of roughly 2 MHz on the laser-cooling transition). These values are much smaller than the typical laser beam waist (w) of 40 μm and transition linewidth (δν) of 20 MHz, respectively. It is therefore justified to apply a linear approximation where the laser intensity is linearly dependent on ion position and the scattering rate is linearly dependent on the ion velocity [18]. Figure 1 illustrates the model and the linear approximations involved. We can therefore write the force on the ion approximately as

$$F_x=F_0+\hbar k\left( \frac{\partial R}{\partial y}\right) y + \hbar k\left( \frac{\partial R}{\partial{\dot x}}\right) \dot x$$

(7)

where R is the rate of scattering of photons (each of momentum $\hbar k$), and the laser is parallel to the x axis. Neglecting F ₀, which is a constant force leading simply to a displacement of the origin of the motion, this equation can be rewritten as

$$F_x=-2m\alpha y-2m\beta \dot x$$

(8)

where m is the mass of the ion, and α and β can we written in terms of the photon scattering rate, given by

$$R={\frac{SA_0}{2}}{\frac{1}{1+S+D^2}}.$$

(9)

Here $D=2(\nu-\dot x/\lambda)/\delta\nu$  is a normalised velocity-dependent detuning and $S=S_{0}\exp(-Y^{2})$ is the position-dependent saturation parameter expressed as a function of the normalised position $Y=\sqrt{2}(y_{0}-y)/w$. In these equations the laser beam has an offset from the origin of y ₀ and a detuning from resonance of ν. The constant A ₀ = 2πδν is the Einstein A-coefficient of the laser-cooling transition.

Fig. 1

a Diagram showing the experimental situation assumed in the laser-cooling model. The Gaussian on the left shows the intensity of the beam as a function of y and indicates the changing intensity experienced by the ion as it moves counter-clockwise in the trap. The orbit of the ion is shown exaggerated for clarity. b If the amplitude of an ion’s motion is small compared to the waist of the beam, the variation in scattering rate R as a function of y is approximately linear. c Similarly, if the ion velocity is small then the change in Doppler shift as the ion oscillates is small compared to the linewidth of the transition and so the change in scattering rate as a function of $\dot x$ is approximately linear

Using these definitions, the equations of motion of the ion take the form

$$\ddot x+\varOmega\dot y+2\beta\dot x- {\frac{\omega_z^2}{2}}x+2\alpha y=0$$

(10)

$$\ddot y-\varOmega\dot x- {\frac{\omega_z^2}{2}}y=0.$$

(11)

These can be written in an approximate form as a single complex equation

$$\ddot u-i\varOmega\dot u+\beta\dot u- {\frac{\omega_z^2}{2}}u-i\alpha u=0,$$

(12)

where the particle position is written as a complex number u = x + iy [19]. This equation can be solved to give cooling rates for the cyclotron and mangetron motions, which are given by

$$\gamma_c={\frac{\beta\omega_c-\alpha}{2\omega_1}}$$

(13)

$$\gamma_m={\frac{\alpha -\beta\omega_m}{2\omega_1}}.$$

(14)

Global cooling of the motion of the ion can only be achieved if both of these quantities are positive. This places a restriction on the values of α and β, namely

$$\omega_m<\alpha/\beta<\omega_c.$$

(15)

For typical values in our experiments, with a magnetron frequency of ω _m  = 2π × 10 kHz and a modified cyclotron frequency of ω _c  = 2π × 700 kHz, typical laser parameters corresponding to strong laser cooling give α/β = 2π × 50 kHz, so that this inequality is satisfied. But the values of α and β are highly sensitive to the laser parameters (intensity, offset and detuning) so their ratio can be varied over a wide range of values.

3.3 Damping force

The effect of the interaction between an atomic particle and a laser beam is often described in terms of a damping force, as reflected in the name “optical molasses” that is sometimes used to describe laser cooling in the case of neutral atoms. The effect of a pure damping force is simply to reduce the velocity exponentially to zero. The damping is represented in the equation of motion by a term of the form $\beta\dot u$.

This simple view does not hold for an offset laser beam because this also supplies angular momentum to the particle. The damping term arising from the laser cooling in Eq. 12 is $(\beta\dot u-i\alpha u)$. The term in β is what is expected in any conventionally damped system. The additional term in α acts to give a torque on the particle that is proportional to its displacement from the origin. If we evaluate the total damping term in a frame rotating at an angular frequency of $\varOmega_{0}$ with respect to the laboratory frame, we find that in this frame it has the conventional form $\beta\dot u$, if $\varOmega_{0}$ has the value α/β. In other words, the damping force acts in a conventional manner in a frame rotating at $\varOmega_{0}$. It is as if the particle is immersed in a fictitious damping medium that is rotating at a fixed frequency $\varOmega_{0}$ (rather like a whirlpool). We will see the significance of this for ICCs in Sect. 4.1. Note that the criterion for laser cooling of both motions (Eq. 15) can now be written as $\omega_{m}<\varOmega_{0}<\omega_{c}$.

4 Ion Coulomb crystals in the Penning trap

4.1 Crystal rotation

The presence of the magnetic field in the Penning trap has the consequence that a trapped cloud of ions always rotates around the centre of the trap. An equilibrium is then set up between the trapping forces, the Coulomb repulsion between the ions, and the centripetal force that leads to a number density given by the following expression [8, 20, 21]:

$$n=2\epsilon_0m\varOmega_{{\rm rot}}(\varOmega-\varOmega_{{\rm rot}})/e^2$$

(16)

where $\varOmega_{{\rm rot}}$ is the angular rotation frequency of the cloud in the laboratory frame. This means that if the rotation frequency of the cloud changes, the cloud can remain in equilibrium by adjusting its number density. In other words, there are many different possible equilibrium states for a given cloud. The aspect ratio of the cloud is also determined by the rotation frequency.

When ions in a Penning trap are laser cooled with a radial cooling beam (perpendicular laser cooling), two processes occur at the same time. One is the reduction of thermal velocities (this can also equivalently be seen as a cooling of the many internal modes of the cloud). As a result of this, collisions between the particles are reduced and, if cold enough (see Eq. 1), they settle into a configuration where their relative positions are fixed (i.e an ion Coulomb crystal).

The second effect is that the laser beam applies a torque to the cloud that can move it towards a particular equilibrium rotation state. Torques can also arise from imperfections in the construction of the trap [22], but because of the small size of the crystals under consideration here, these torques are expected to be much smaller than that due to the laser beam. The final state of the system will be one where the average torque on the ions is zero. From a consideration of the discussion in Sect. 3.3, we can see that in the absence of other factors the equilibrium rotation frequency will be $\varOmega_{0}$. In other words, the crystal will rotate at the same rate as the fictitious damping medium discussed in Sect. 3.3. If the rotation frequency differs from this value, the torque arising from the rotating damping force will tend to speed up or slow down the crystal rotation until it matches $\varOmega_{0}$. It should therefore be possible to control the number density of the ion cloud or crystal by suitable adjustment of the laser-cooling parameters to alter $\varOmega_{0}$. Note, however, that this will only be the case if the crystal radius is less than the beam waist w, so that the linear approximations of Sect. 3.2 are valid.

It is instructive to consider typical values for the parameters of the ICC. If the radius of the crystal is 10 μm, and $\varOmega_{{\rm rot}}/2\pi = 100$ kHz, then the speed of an ion at this radius is 6 m/s and (for calcium) the maximum Doppler shift is 15 MHz. For a laser beam waist of 40 μm and a transition linewidth of 21 MHz, the approximations illustrated in Fig. 1 are therefore reasonably valid, so long as the laser detuning is not too small. However, for crystals with a larger radius these approximations begin to break down, as discussed in Sect. 5.2 below.

Using Eqs. 7 and 8 we can write $\varOmega_{0}$ as

$$\varOmega_0=\alpha/\beta=\left.\left( \frac{\partial R}{\partial y}\right) \big/ \left( \frac{\partial R}{\partial\dot x}\right) \right.$$

(17)

In Sect. 5, we show through simulations that for realistic parameters of the trap and laser, the rotation frequency of the crystal is indeed determined mainly by the laser parameters, in the absence of other competing effects.

The authors of Ref. [22] investigated the behaviour of a larger cloud of ions with a single perpendicular laser-cooling beam, as discussed here. The rotation frequency of the cloud was assumed to be determined by a balance between the torque from the laser beam and a torque due to field imperfections. The authors were then able to predict and measure the equilibrium radial temperature of the ions. However, in this case, the ion cloud was larger than the laser beam. In our case, the ICC is smaller than the laser beam, and the torque due to the field imperfections can be ignored. The equilibrium conditions are therefore determined by the laser beam parameters alone. The simulations reported here are not able to make any predictions concerning the temperature of the ions.

It is interesting to compare the situation of the Penning trap with a radio-frequency trap. It is of course also possible for an ion crystal in a radio-frequency trap to rotate, but there are two effects that lead to this being unlikely. One is that generally the laser-cooling beam will not be displaced from the centre of the trap, so there will be no torque present. The other reason is that the trap in general will not have perfect radial symmetry so the two radial oscillation frequencies will not be degenerate, and this will tend to prevent the crystal from starting to rotate. In the Penning trap, on the other hand, the crystal will always rotate due to the presence of the magnetic field. It is therefore much easier for the laser to control this rotation.

4.2 Axial crystals

At a sufficiently low axial confining potential, the equilibrium configuration of the ions (in both Penning and radio-frequency traps) is a linear string along the axis of the trap. This is the simplest type of Coulomb crystal and has been used in many experiments with trapped ions, as discussed in Sect. 1.

A perfectly linear string cannot normally be said to rotate, but we describe here a sense in which it is appropriate to describe the oscillation of a linear string that has undergone a small zigzag perturbation as a rotation. The linear string has normal modes of oscillation, like any other structure made up of a number of particles. Consider the linear string of ions in the rotating frame R introduced earlier. The lowest-frequency vibrational mode is always a transverse mode. In this mode, the ions oscillate in a zigzag configuration where the ions are still confined to a plane but adjacent ions are always on opposite sides of the trap axis. As the axial confining potential is increased, the frequency of this mode gradually decreases until it becomes equal to zero. At this point, there is a transition to a stable zigzag configuration [23]. Each ion is then permanently displaced from the axis, with the ions nearest to the centre of the string having the largest displacements. The magnitudes of all the displacements increase as the axial confinement is further increased, and eventually the crystal adopts more complicated, three-dimensional structures. Each transition from one structure to another can be characterised by the ratio of the confining strengths in the radial and axial directions, and some of these have been calculated by Rafac et al. [24] (see also [8]). We define μ as the ratio of radial to axial strengths, i.e. μ = ω ² _r /ω ² _z , at the transition from the linear to the zigzag configuration. For three ions, this transition (here to a simple kink) takes place at μ = 2.4 and for four ions, it takes place when μ = 4.15.

We define ω _zz to be the angular frequency of the zigzag oscillation of a linear string in the rotating frame. There are two degenerate modes, and we can take these to be a clockwise and an anticlockwise rotation about the trap axis at ω _zz (for small amplitudes). When transformed into the laboratory frame, this would be seen as a rotation of the (perturbed) string at a frequency of $\omega_{zz}^{\prime}=\varOmega/2 - \omega_{zz}$ (the component at $\varOmega/2 + \omega_{zz}$ is not important for this discussion). Once the linear string is perturbed in this way, the rotation described is a stable mode of oscillation of the system, in the absence of other damping mechanisms.

In order to calculate the value of the zigzag vibrational frequency in the rotating frame (ω _zz ), we note that the crystal adopts a stable zigzag configuration when the ratio of confinement strengths is equal to μ in a frame in which the crystal is stationary (call this frame C). But if the crystal is itself rotating at a frequency $\varOmega_{R}$ relative to the frame R, then the effective strength of confinement in the radial direction in frame C (ω _cryst ) is related to that in frame R (ω ₁) by

$$\omega_{\rm cryst}^2=\omega_1^2-\varOmega_{R}^2$$

(18)

by a straightforward consideration of the outward centrifugal force in the frame C. Therefore, if in the crystal frame C, the crystal is exactly at the critical point (so it can just sustain a small zigzag perturbation), ω ² _cryst /ω ² _z  must be equal to μ and ω _zz must be equal to $\varOmega_{R}$, giving

$$\omega_{zz}^2=\omega_1^2-\omega_{{\rm cryst}}^2=\omega_1^2- \mu\omega_{z}^2=\varOmega^2/4-(\mu+1/2)\omega_{z}^2.$$

(19)

We therefore now have an equation for the rotation frequency of a small zigzag perturbation of the linear string in the rotating frame R. In the laboratory frame, the observed rotation frequency will therefore be $\omega_{zz}^{\prime}$ which is given by

$$\omega_{zz}^\prime=\varOmega/2 - \omega_{zz}={\frac{\varOmega}{2}}-\sqrt{\varOmega^2/4-(\mu+1/2)\omega_z^2}.$$

(20)

5 Simulations

5.1 Simulation program

In order to investigate the behaviour of small ICCs in a Penning trap, we carried out simulations taking into account all the forces on the ions including those arising from the electric and magnetic fields, the Coulomb interaction between ions and the effects of the laser-cooling beams (one along the axis and one in the radial plane of the trap). The simulations were carried out in the laboratory frame.

Simulations were conducted by performing time-discretised numerical integration of the equations of motion of each particle in the trap, using analytical expressions for the forces due to the trapping fields, the Coulomb repulsion of the ions and the laser beam. The force due to the laser beam was evaluated explicitly, without making the linear approximations illustrated in Fig. 1: the laser beam profile was Gaussian and the frequency response of the ions was described by a Lorentzian profile. At each discrete time step, the total force on each ion was evaluated. Each particle’s motion over the time step was then approximated using a fourth order Runge–Kutta algorithm that performed numerical integration on the acceleration of the particle. Programs were written in C++, which was chosen for its balance of computational speed and ease of development.

The particles simulated were Ca⁺ with a laser-cooling wavelength corresponding to the S_1/2 to P_1/2 transition. The transition linewidth is δν = 21 MHz. Although the P_1/2 level can also decay (with a small branching ratio) to the metastable D_3/2 level, this decay was ignored as in experiments any ions that decay to this level are rapidly repumped into the cooling cycle by an additional laser beam. Re-emission of photons was not included as we were not concerned with the residual thermal motion of the ions but just with the global structure and rotation of the ICC. This reduced the computational effort required in the simulations. However, this means that no information is obtained on the temperature of the ions.

The laser beams were implemented using realistic parameters for the laser intensity and the beam waist. Simulations were carried out for different values of the offset of the beam and the laser detuning from resonance. In order to speed up the simulations, the photon momentum was artificially increased but simulations were also carried out without this change, in order to check that it did not affect the final result.

The correct operation of the simulation program was checked using it to simulate situations with known behaviour, such as the motion of a single ion in the absence of a laser beam, laser cooling of a single ion and the analytically calculable motion of crystals containing 2–4 ions.

The ions were started with random initial positions and speeds corresponding to an initial temperature of 5 K in order to limit the computational time required to reach equilibrium. In this work, the main interest was in the equilibrium final state, so different criteria were applied to determine when this equilibrium was reached. It was not sufficient simply to look for a state to be reached where, for example, the total energy of the system was constant. This is because as each ion moves within the profile of the laser beam, the force F ₀ in Eq. 7 changes, leading to fluctuations in the energy of the system. The scheme finally adopted was based on an analysis of the Fourier transform of the energy of the system. Fourier transforms of the potential energy were taken at regular intervals, and the individual components of the transforms compared. If no component had changed by more than a set value between two samples, the crystal would be declared stable.

The output of the simulation included the positions and fluorescence intensity of all particles. From these data, it was possible to extract the angular velocity of each particle, even in the case of an axial string. This is because the interaction with the laser beam is sufficient to give rise to a small perturbation in the configuration of the string, which excites the zigzag mode; the motion of this perturbation can then be followed as a function of time.

5.2 Simulation results

As an example of the output of the program, Fig. 2 shows several different final configurations of four ions for different axial confining potentials. At the lowest axial confinement (i.e. low applied voltage) the configuration is a linear string along the axis. As the strength of the confinement increases, the configuration changes through planar and solid (tetrahedral) structures until at the strongest confinement it forms a square in the radial plane.

Fig. 2

Simulated configurations of a four-ion crystal for different strengths of axial confinement. The image at the top left has the weakest axial confinement, and the image at the bottom right has the strongest axial confinement. The z-axis is vertical in these images

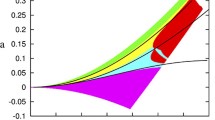
In Fig. 3, the angular velocity of a four-ion crystal in the laboratory frame is shown as a function of laser detuning for two different offsets of the laser beam, which has a waist of w = 40 μm. The normalised detuning D ₀ is expressed in units of δν /2. A theoretical curve (from Eq. 17) is also shown for comparison. It can be seen that for both values of the laser offset the crystal rotates at a frequency equal to that of the damping force provided by the laser (within the uncertainty of the measurement of angular velocity in the program). The fluorescence from the crystal is strongly dependent on the laser parameters and in particular it drops steadily as the laser detuning is increased, as expected. Note that the crystal structure changes as the detuning changes in these simulations.

Fig. 3

Plot of the angular velocity of a four-ion crystal in the laboratory frame as a function of the normalised detuning (D ₀). These simulations were carried out at a relatively high potential (A = 100 kV/m²) with a laser offset of y ₀ =  − 60 μm (red, squares) and y ₀ =  − 40 μm (black, circles). Theoretical predictions are shown dashed

In order to show that the rotation frequency is independent of the applied voltage, simulations were carried out for 15 ions with a range of trap potentials. Figure 4 shows that the frequency of rotation of the crystal is essentially independent of the applied potential. However, in order to maintain the same rotation frequency, the configuration of the crystal changes with the potential.

Fig. 4

Plot of the angular velocity of the crystal as a function of normalised detuning (D ₀) for simulations using 15 particles. The laser offset was y ₀ =  − 60 μm. Coloured lines show simulation results for different trap potentials. Dashed black line shows same theoretical curve as in Fig. 3

The agreement with the theoretical line is not so close for 15 ions as it is with four ions. This is because the radial extent of the crystal is larger. In particular, at low laser detunings, the measured rotation frequencies deviate significantly from the theoretical curve. In this region, the crystal is oblate and extends beyond the edge of the laser beam. The Doppler shift of the outer ions is also larger than the linewidth of the transition. The linear approximations made in Eq. 7 and illustrated in Fig. 1 are therefore no longer valid. In fact, at low detunings, the observed rotation is faster than predicted under these circumstances. This has also been observed in experiments in our laboratory [25].

At a given rotation frequency, the crystal becomes more prolate as the confining potential is reduced. Eventually, as discussed in Sect. 4.1, the crystal becomes a string along the trap axis and is no longer able to adjust its density to satisfy Eq. 16. At this point, the rotation frequency ceases to be determined by the laser parameters, as shown in Fig. 5. It can be seen that for both laser offsets, the limiting rotation frequency of the crystal is the same and only depends on the axial potential. Comparison with Eq. 19 shows that this equation correctly predicts the limiting frequency.

Fig. 5

Plot of the rotation frequency of a four-ion crystal against laser detuning for a laser beam offset of −40 μm (squares) and −60 μm (circles). The dotted lines show the calculated values of $\omega_{zz}^{\prime}$ for each trap potential

The maximum rotation frequency of the crystal in the rotating frame ($\omega_{zz}^\prime$) increases as the applied potential increases because the crystal is then able to spin faster before it becomes a string. However, there is a point where this maximum frequency becomes equal to $\varOmega/2$, at which point the density of the crystal is maximum (this is often referred to as “Brillouin flow”). At even higher voltages, the crystal never becomes a string. This is illustrated in Fig. 6.

Fig. 6

Plot showing the maximum rotation frequency ($\omega_{zz}^\prime$) of a four-ion crystal for various values of trap potential. The error bars show the range of rotation frequencies in different simulations, and the point shows the average. The theoretical line is from Eq. 20

6 Conclusions

We have shown that, in the absence of other forces, an ICC in a Penning trap adjusts its properties (i.e. its structural configuration and density) so that it rotates at a frequency set by the parameters of the laser beam. However, if the laser parameters dictate a frequency that is higher than the frequency at which the crystal becomes a linear string, the crystal is no longer able to follow the laser and instead it simply oscillates in its lowest transverse oscillation mode (the zigzag mode), at a frequency that depends only on the applied trap voltage. These predictions have been confirmed by detailed computer simulations. Using photon−photon correlation techniques, this behaviour should also be testable in the laboratory.