1 Introduction

Optical fibers cannot just transmit pulses of light: They can also be useful tools for shaping them. Based on the simultaneous action of anomalous dispersion and Kerr nonlinearity, pulses can be temporally compressed through a mechanism known as soliton compression [1, 2]; as pulse energy is preserved in the process, the peak power grows accordingly.

The process of modulation instability, by comparison, bestows exponential growth on a weak pulse that rides on a continuous wave background which provides the energy [3]. Probably the first discussion to use this effect for the generation of a train of short pulses was given in [4]. In that reference, it is also proposed to remove the continuous background by the polarization technique introduced in [5]. On several subsequent occasions, the possibility to generate trains of short pulses was pointed out, and the cw background was commented upon [6–9]. The background can also be removed by the Raman effect [9]. We will place this discussion in a more general context here. Modulation instability is the name commonly attached to the phenomenon that a continuous wave, under conditions of anomalous dispersion, is an unstable solution of the nonlinear Schrödinger equation that governs pulse propagation in optical fibers. In a more general framework, one can specify the stable solutions the system will tend to when it moves away from the continuous wave. While mathematically known for many years, these solutions were demonstrated in experiments only very recently: What is now known as the Akhmediev breather [10] was first seen in [11] and described in more detail in [12], the Peregrine soliton [13] was first seen in [14], and the Kuznetsov-Ma soliton [15, 16] was first seen in [17].

All three solution types share the property that there is a modulation on top of a continuous background. We discuss here the case that the background is removed in an interferometer. This is easily possible thanks to the clean phase structure of all solution types, and it can be tightly controlled—presumably better than alternative techniques by polarization or Raman effect which we do not pursue here. We present quantitative results on the pulse durations and peak powers that can be obtained. In two out of three cases, one can start from a very weak (basically, infinitesimal) perturbation and exploit the exponential gain inherent in the process. A very recent experiment reported in [18] deals with one of the three cases in just the manner discussed here; it demonstrates that this approach is viable and leads to good results. We will also comment on the question whether the pulses thus generated can become solitons in the same fiber.

The paper is structured as follows: After setting up all relevant equations and conditions in Sect. 2, we will treat the three cases of AB, PS and KM in Sects. 3, 4, and 5, respectively. In Sect. 6, we discuss the much disputed question [4, 6, 8, 9] how well the generated pulses approximate a soliton in the same fiber.

2 General properties of a family of solutions

The propagation of light pulses in optical fiber is governed by the nonlinear Schrödinger equation [19, 20] which can be written in the form

$$\frac{\partial A}{\partial z} = i \frac{\beta_2}{2} \frac{\partial^2 A}{\partial T^2} + i \gamma |A|^2 A$$
(1)

where A = A(T, z) is the complex field envelope in a comoving frame of reference. T denotes time, z the position, γ the nonlinearity coefficient, and β 2 the group velocity dispersion coefficient. For clarity, we will here disregard any higher-order corrections to nonlinear or dispersive behavior. Eq. (1) has several solutions of which solitons are discussed particularly frequently [19, 20]. We will turn to them below, but first we consider the expression [10]

$$A(a,Z,T) = \sqrt{P_0} \frac{(1-4a)\;\hbox{cosh}(bZ) +ib\; \hbox{sinh}(bZ) + \sqrt{2a}\;\hbox{cos}(\omega_{\rm m} T)}{\sqrt{2a} \;\hbox{cos}(\omega_{\rm m} T) - \hbox{cosh}(bZ)} \exp(iZ)$$
(2)

with the real parameter a ≥ 0 and the derived complex quantity \(b=\sqrt{8a-16a^2}\). Position is here normalized to the nonlinear length by Z = z/L NL = γ P 0 z. Power level is set by P 0, and the time scale by

$$\omega_{\rm m}=\sqrt{1-2a}\,\omega_{\rm c} \quad \hbox{with} \quad \omega_{\rm c}=\sqrt{\frac{4\gamma P_0}{|\beta_2|}}.$$
(3)

Equation (2) describes different solutions, depending on a. They all share the property that they can be written as modulation on a finite background. We illustrate this by recasting Eq. (2) as

$$A(a,T,Z) = \sqrt{P_0} [1 + M(a,T,Z)]\,\hbox{exp}(iZ),$$
(4)

where the modulated part can be written as

$$M(a,T,Z)\left\{ {\begin{array}{*{20}c} {\frac{{2(1 - 2a)\;{\text{cosh}}(bZ) + ib\;{\text{sinh}}(bZ)}}{{\sqrt {2a} \;{\text{cos}}(\omega _{{\text{m}}} T) - {\text{cosh}}(bZ)}}} \hfill & {:\quad 0 < a < \frac{1}{2}} \hfill \\ { - \frac{{4(1 + 2iZ)}}{{1 + \omega _{c}^{2} T^{2} + 4Z^{2} }}} \hfill & {:\quad a = \frac{1}{2}} \hfill \\ {\frac{{2(1 - 2a)\;{\text{cos}}(|b|Z) - i|b|\;{\text{sin}}(bZ)}}{{\sqrt {2a} \;{\text{cosh}}(|\omega _{{\text{m}}} |T) - {\text{cos}}(|b|Z)}}} \hfill & {:\quad a > \frac{1}{2}} \hfill \\ \end{array} } \right.$$
(5)

For 0 < a < 1/2, one obtains the Akhmediev breather (AB), a structure with oscillating time dependence. In this case, the solution develops from a continuous wave; a modulation grows and eventually culminates into a periodic chain of peaks, then decreases and leaves a continuous wave. The AB is, in other words, localized in position (at the culmination point), and periodic in time. Conversely, in the case a > 1/2, one has the Kuznetsov-Ma (KM) soliton. This is a structure which is localized in time and periodic in space. The singular case in between is the Peregrine soliton (PS) at a = 1/2, which is localized in both domains, i.e., has a single peak. 1/|b| is a characteristic length scale for AB and KM which diverges for PS.

The aim in all three cases is to let the structure propagate up to the culmination point. There, the modulation takes the global minimum of temporal width, and the global maximum of peak power given by

$$|A(a,0,0)|^2 = \hat{P}_{{\rm culm}} = P_0 \left(1+\sqrt{32a}+8a\right).$$
(6)

Inspection of Eq. (2) reveals that for the cases of AB and PS (real-valued b), |A(a, T, Z)| tends to the constant \(\sqrt{P_0}\) as \(Z \rightarrow \pm \infty\). For |Z|≫ 1, there is a weak modulation of both amplitude and phase superimposed on the constant background which is well approximated by a harmonic oscillation. Toward Z = 0, the modulation depth grows until the peaks culminate as in Eq. (6), and thereafter they evolve back and disappear for \(Z \rightarrow \infty\). In the KM case, there is always an oscillatory modulation with spatial frequency 2π/|b|, see in Sect. 5 below. At its minimum, e.g., at Z =  − π/|b|, the power is

$$P_{\hbox{min}}^{{\rm (KM)}} = P_0 \left(1 -\sqrt{32a} + 8a\right).$$
(7)

In practice, to generate the case of a targeted a, one will launch a continuous wave with a modulation. Particulars are covered by Eq. (5); one has to mimic the modulation at some chosen initial Z. With \(P_0,\;\beta_2\) and γ given, one chooses a and determines the corresponding frequency.

For the AB, this is done according to Eq. (3). One can use harmonic modulation of very small depth which approximates Eq. (5) at |Z| ≫ 1 quite well. The modulation depth, by virtue of the exponential gain, sets the Z position of the starting point and thus determines the fiber length to the culmination point. Simultaneous amplitude and phase modulations of the carrier are required so that the phasor of the modulated carrier traces out a straight line in the complex plane. For the KM, Eq. (3) yields an imaginary value; the real-valued frequency is chosen according to the modulus. The most practical method is to chose a modulation at minimum at Z =  − π/|b| and in the form as in Eq. (7); here, pure amplitude modulation suffices because modulation and carrier are in phase at all minima of the modulation. The fiber length to culmination is then automatically fixed to one half of the spatial period. In either case, one needs nothing more than amplitude and phase modulators; neither a second light source nor any sophisticated phase matching is required.

Here, we suggest to eliminate the constant background as seen in Eq. (4) by using a Mach–Zehnder interferometer. Nulling the background by destructive interference requires that the arm lengths are set for a suitable path difference and that the two amplitudes are equal; best efficiency is obtained with 50:50 beam splitters. Then in one of the outputs (but not the other, of course), the background is eliminated, while the pulse amplitude will be attenuated by a factor of F = 1/2 since each beam splitter contributes a factor of \(1/\sqrt{2}\).

In the long-standing debate how the peaks generated by MI are related to solitons, it was recently shown how the structure of the AB can be analyzed for its soliton content [21]. For that discussion, it is essential to realize that reality poses the constraint that the AB is finite in length—both in experiments and in numerical simulations. Such a truncated AB does contain a number of solitons, but it would be wrong to identify the individual peaks with individual solitons. It was also shown that pulses separated from the background by the Raman effect are indeed solitons ‘set free.’

3 Akhmediev breather

First, we consider the case a < 1/2. In real-world experiments with finite fiber lengths, the AB can be generated by applying a weak modulation of the carrier as a seed [12]. The modulation depth can, in principle, be arbitrarily small if the fiber length is chosen accordingly. Practically speaking, a limit to this will be set by noise considerations: To maintain tight control over the process, the modulation depth should well exceed the noise floor. The carrier is ideally a continuous wave, but in experiments, it may well be replaced by a very wide background pulse. One lets the modulation grow up to the culmination point where the fiber is terminated, and the light enters the interferometer. The path difference of the interferometer arms should amount to a travel time difference of \(\Updelta T=\pi/\omega_{\rm m}\); this way, the best background suppression is obtained. The output then takes the form

$$S^{{\rm (AB)}}(T,0) = F \sqrt{32aP_0}(1-2a) \frac{\hbox{cos}(\omega_{\rm m} T)}{2a\;\hbox{cos}^2(\omega_{\rm m} T)-1}$$
(8)

which is a train of pulses with alternating phases. In the power profile, the repetition frequency is doubled.

The temporal width (we use τ for full width at half maximum throughout) of the pulse train generated with this method is

$$\tau^{{\rm (AB)}} = \frac{2}{\omega_{\rm m}} \left[\pi -\hbox{arccos}\left( \frac{\left| 2 a-1\right|-\sqrt{4 {a}^{2}+1}}{\sqrt{8} a}\right)\right],$$
(9)

and the peak power is

$$\hat{P}_{{\rm out}}^{{\rm (AB)}}=F^2 32 a P_0.$$
(10)

The time scale is set by 1/ωm; other than that, the width is solely dependent on a. The power scale is set by P 0; other than that and with F = 1/2 fixed as above, the peak power is proportional to a; a fourfold increase over the cw power is possible. In Fig. 1, the duration is plotted in units of the modulation period T mod = 2π /ωm; in this format, the obtained temporal compression is immediately apparent to be considerable. Alternatively, the width is also shown normalized to the scaling time

$$T_{{\rm scale}}=\sqrt{\frac{|\beta_2|}{\gamma P_0}} ;$$
(11)

this facilitates calculation of absolute duration to be expected for different fibers and cw powers.

Fig. 1
figure 1

Width of pulses generated from the Akhmediev breather, normalized to the modulation period (solid curve and left axis) and to the scaling time Eq. (11) (dashed curve and right axis)

Full size image

4 Peregrine soliton

This same method can also be applied to the PS. It is convenient that the interferometer’s travel time difference \(\Updelta T\), while it must be larger than the pulse width, can otherwise be chosen arbitrarily as there is no risk that subsequent pulses interfere with each other. The sum field then reduces to a scaled version of M(1/2, T, 0) which is

$$S^{{(PS)}} = F\frac{{ - 4\sqrt {P_{0} } }}{{1 + \omega _{{\text{c}}}^{2} T^{2} }} .$$
(12)

The peak power is

$$\hat{P}_{\hbox{out}}^{{\rm (PS)}} = F^2 16P_0,$$
(13)

which is consistent with Eq. (10). [Note that Eq. (6) still contains the background]. The width of the resulting peak is

$$\tau ^{{({\text{PS}})}} = \frac{2}{\omega }_{{\text{c}}} \sqrt {\sqrt 2 - 1} ;$$
(14)

two such pulses at a separation of \(\Updelta T\) will emerge from the interferometer.

5 Kuznetsov-Ma soliton

For a > 1/2, one has to consider that the KM soliton is periodic in space. Maxima occur at \(Z = n \cdot 2 \pi/|b|\) with \(n \in \tt{N}\), minima at half-integer multiples. Minima are the natural launch points to obtain the benefit from amplitude growth. At Z = π/|b|, the modulated part of the field envelope takes the form

$$M_{{\rm min}}^{{\rm (KM)}}=\frac{4a-2}{\sqrt{2a}\;\hbox{cosh}(|\omega_{\rm m}| T)+1}.$$
(15)

The input pulse power thus should be chosen as

$$\hat{P}_{{\rm in}}^{{\rm (KM)}} = 4 P_0(\sqrt{2a}-1)^2,$$
(16)

and its width

$$\tau_{{\rm in}}^{{\rm (KM)}} = \frac{2}{|\omega_{\rm m}|}\;\hbox{arcosh} \left(-\frac{1}{\sqrt{2a}}+\frac{1}{\sqrt{a}}+\sqrt{2}\right).$$
(17)

After propagation up to Z = 0, the fiber is terminated, and the signal is steered into the interferometer. Again, the temporal shift \(\Updelta T\) in the interferometer can be chosen arbitrarily as long as it exceeds the pulse duration. The sum field, like in the Peregrine case, is a scaled version of M(a, T, 0):

$$S^{{\rm (KM)}}=F \frac{2(1-2a) \sqrt{P_0}}{\sqrt{2a}\; \hbox{cosh}(|\omega_{\rm m}| T)-1}.$$
(18)

The peak power thus achieved is

$$\hat{P}_{{\rm out}}^{{\rm (KM)}} = F^2 4P_0(\sqrt{2a}+1)^2.$$
(19)

Its dependence on a is shown in Fig. 2 together with the required power of the input modulation.

Fig. 2
figure 2

Power of pulses generated from the Kuznetsov-Ma soliton, shown together with required input power. Both are normalized to the initial cw power

Full size image

The width of the resulting peak is

$$\tau^{{\rm (KM)}} = \frac{2}{|\omega_{\rm m}|}\; \hbox{arcosh}\left(\sqrt{2 - \sqrt{\frac{8}{a}} + \frac{1}{a}}+\frac{1}{\sqrt{2a}}\right).$$
(20)

The value of τ(KM)(a) is shown in Fig. 3, normalized to the duration of the input modulation and to the scaling time T scale, respectively.

Fig. 3
figure 3

Width of pulses generated from the Kuznetsov-Ma soliton, normalized to width of input modulation (solid curve and left axis) and to the scaling time T scale (dashed curve and right axis)

Full size image

Contrary to the AB and PS cases where in principle unlimited gain is available, here the gain cannot exceed the ratio between peak powers at output and at launch. The ratio of generated output peak to invested modulation peak is obtained from evaluation of Eq. (5) at a > 1/2 with consideration of the factor F 2 from the interferometer. One obtains

$$\frac{\hat{P}_{{\rm out}}^{{\rm (KM)}}}{P_{{\rm mod,in}}} = F^2 \frac{1 + \sqrt{8a} + 2a}{1-\sqrt{8a}+2a}.$$
(21)

This becomes smaller than unity at a = 4.5; obviously an undesired situation.

6 Can solitons be formed?

In Fig. 4, we visualize how a train of short pulses can be formed according to the above discussion. For the picture, we selected the case of an AB at a = 0.48 shown in Fig. 4a, b displays the resulting pulse train as coupled out from the interferometer.

Fig. 4
figure 4

a Power profile of an Akhmediev Breather (a = 0.48) at the culmination point (Z = 0). b Power profile of the background-free pulse train generated from it by the interferometer

Full size image

The question now arises naturally whether the pulses thus generated can form solitons in the same fiber where the above solutions have been excited. The fundamental soliton solution of the nonlinear Schrödinger equation Eq. (1) can be written as [19, 20]

$$A(T,z) = \sqrt{P_0}\,\hbox{sech}\left( \frac{T}{T_0} \right) \exp \left(\frac{i Z}{2}\right)$$
(22)

except for trivial coordinate shifts. Characteristic is the sech shape of this solution, with a width

$$T_0 = \frac{\tau}{2\;\hbox{arsinh(1)}}\approx\frac{\tau}{1.763}.$$
(23)

There is a constraint linking peak power \(\hat{P}\) and width:

$$\hat{P} T_0^2 = N^2 \frac{|\beta_2|}{\gamma}.$$
(24)

The quantity N is known as the soliton order. For N = 1, one has the fundamental soliton, higher integer values correspond to higher-order solitons [19, 20, 22]. Deviations from integer values are indicative that in addition to solitons, there is also continuous radiation. For N < 1/2 no soliton exists. Again, we discuss the three types of solutions in turn.

For the AB one might, as a first rough approximation, assume that the generated peaks have a semblance to a sech shape. Then, by virtue of Eq. (24), the soliton number N can be estimated from

$$N^2 = \frac{\gamma}{|\beta_2|}\hat{P}_{\hbox{out}}^{{\rm (AB)}} T_0^2.$$
(25)

Inserting \(\hat{P}\) from Eq. (10) and T 0 from Eqs. (9) and (23) one obtains

$$N^2 = F^2 \Uplambda,$$
(26)

where

$$\Uplambda = \frac{8 a}{\hbox{arsinh}^2(1) (1-2a)} \left[ \pi -\hbox{arccos}\left( \frac{(1-2a) -\sqrt{4 {a}^{2}+1}}{ \sqrt{8}\,a}\right) \right]^2.$$
(27)

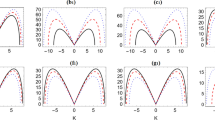
Solitons are formed when \(N \ge \frac{1}{2}\), which demands that \(\Uplambda \ge 1\). As the plot of \(\Uplambda\) versus a in Fig. 5 shows, solitons are formed when a > 0.18. Obviously the best value is close to a = 1/2.

Fig. 5
figure 5

Numerical values for the functions \(\Uplambda(a)\) and \(\Upgamma(a)\) used in this section. For the numerical value at the maximum see Eq. (28)

Full size image

This simple estimate notwithstanding, we turn to a more profound method to determine the soliton content of arbitrarily shaped pulses. The principal tool to obtain information about the soliton content of some structure is the inverse scattering transform (IST) technique originally described for a different equation by Gardner et al. [23] and first applied to the nonlinear Schrödinger equation by Zakharov and Shabat [24]. In its framework, solitons are described through certain discrete eigenvalues; in general, linear radiation is also produced which corresponds to the continuous part of the eigenvalue spectrum. It is of central importance to point out that IST relies on the integrability of the equation, a condition fulfilled here. We use the numerical IST-based technique introduced in [25] and known as direct scattering transform (DST). It requires data which decay to zero for \(T \rightarrow \pm \infty\). This is automatically fulfilled here for the KM and PS after passing the interferometer; for the AB, we used one periodicity interval with zero padding.

At F = 1/2, one finds that the resulting pulse contains a single soliton as 0.25 < a < 0.5. The soliton energy, normalized to the pulse energy, is plotted in Fig. 6. The best conversion efficiency is near a = 1/2, where almost 96 percent of the pulse energy contributes to the soliton.

Fig. 6
figure 6

Fraction of pulse energy that can be converted into a soliton, calculated by direct scattering transform. Note the change of scale at a = 0.5. A fundamental soliton is formed for \(0.25 \le a \le \infty\)

Full size image

For the PS case, a soliton number can be estimated as above when a shape similar to sech is assumed. To this end, we insert Eqs. (13), (14) and (23) in Eq. (24):

$$N^2 = \frac{4(\sqrt{2}-1)}{\hbox{arsinh}^2(1)} F^2 \approx 2.133 F^2.$$
(28)

This is consistent with the limit for \(a\rightarrow\) 1/2 obtained for the AB above.

In the KM case, the approximate soliton number is

$$\begin{aligned} N^2 &= F^2 \frac{(\sqrt{2a}+1)^2}{(2a-1)\;\hbox{arsinh}^2(1)} \hbox{arcosh}^2\left(\sqrt{2-\frac{2^{3/2}}{\sqrt{a}} +\frac{1}{a}}+\frac{1}{\sqrt{2a}}\right)\\ &= F^2 \Upgamma, \end{aligned}$$

where we introduced \(\Upgamma\) which depends only on a; see Fig. 5. For \(a\rightarrow 1/2\), its value coincides with the corresponding value obtained for the PS. From the observation that

$$\lim_{a\rightarrow \infty} \Upgamma^2 = 1 ;$$
(29)

it follows that solitons are formed for all values of a.

Again, we also applied the numerical DST to the generated fields. We obtain confirmation that indeed a single soliton is formed for all a > 1/2. Moreover, we also compared the soliton energy E sol to the total pulse energy \(E_{{\rm pulse}}=\int P(t)\,\hbox{d}t\), as a measure of conversion efficiency. Figure 6 shows the result, along with the same for AB and PS. As stated above, a soliton begins to exist at a = 0.25. The fraction of energy going into the soliton then rises quickly with increasing a, peaks at a = 0.5, and decays again. This shows that large values of a are useless if a soliton is to be generated efficiently.

7 Summary and conclusion

In summary, we present analytical properties of pulse trains as obtained from a continuous wave excitation with a small perturbation, after fiber propagation and shaping in an interferometer. For three cases, namely Akhmediev breather, Peregrine soliton and Kuznetsov-Ma soliton, we show that the pulse properties can be controlled by modulation parameter a; the entire process is specified by the input cw power P 0, fiber parameters β 2 and γ, the fiber length L, and the modulation type and depth.

A modulation of a continuous wave is adequate for excitation of each of the three cases. For the Akhmediev breather and the Peregrine soliton, the modulation can in principle be chosen infinitesimally small, on account of the exponential gain provided by modulation instability. However, in the interest of tight control over the process, the modulation amplitude should exceed the noise floor. After removing the background in a Mach–Zehnder interferometer, the achievable pulse peak power is 4P 0 in the limit \(a\rightarrow 1/2\). For the Kuznetsov-Ma soliton, the effective gain passes through unity at a = 4.5 so that it does not appear useful to consider values beyond that point. In terms of temporal compression (output pulse width versus input modulation period), the parameter region around a≈ 1/2 seems to be most attractive.

Using both an analytical approximation and the numerical direct scattering transform, we also calculated the soliton number of the resulting pulses, as referred to the same fiber. Fundamental solitons are formed for a > 0.25; for a ≈ 1/2 more than 95% of the pulse energy can be converted into an soliton.

Our results show that the method discussed here promises to work quite well. In fact, the recent report in [18], which is about one of the cases treated here, successfully demonstrates the experimental viability of this approach.