1 Introduction

Star sensor is widely used in attitude determination system of many spacecraft, especially in satellites [1–3], which needs high accuracy, nonexcursion and excellent autonomy. The apparent position of the observed stars based on charge-coupled device (CCD) or complementary metal oxide semiconductor (CMOS) sensors can be determined with sub-pixel accuracy by using image processing techniques [4]. The measurement precision of the observed star is mainly determined by the accuracy of the star sensor parameters. Therefore, it is necessary to correct the error of star sensor parameters through calibration. Star sensor calibration can be divided into ground-based initial calibration with static distortions and on-orbit calibration with dynamic distortions [5]. In this work, we only discuss ground-based calibration.

Theoretically speaking, star sensor can be regarded as a camera. So, star sensor can be modeled with the pinhole camera model which is just a perspective projection followed by an affine transformation in the image plane. The previous calibration models that are based on the assumption of the small field of view (FOV) usually relate to the principal point and the focal length only and do not need to take the influence of other factors into account [6]. However, with a new generation of star sensor which is characterized with wider FOV, ideal pinhole model is not accurate. Furthermore, most of the calibration methods require high-precision calibration devices to guarantee the high calibration precision. High-precision calibration devices mean low installation error and expensive. To consider installation error will reduce the demand of calibration devices. Hence, comprehensive factors should be taken account into star sensor calibration.

Up to now, many researchers have done a lot of work on star sensor calibration [4, 6–9]. Literature [4] and [9] calibrated focal length and the principal point using the standard nonlinear least-squares estimation. Those literatures only calibrated the principal point, and focal length of star sensors and the results were easily affected by noise. Literature [7] did calibration with lens distortion and analyzed in theory. Unfortunately, it cannot be applied to the real data. Literature [8, 10, 11] proposed optical laboratory star sensor calibration methods that require high-precision calibration device and assume that no error in the setup process. Though literature [12] took installation error into account in the laboratory star sensor calibration, the iterations of installation error need to be given manually. As present previously, these methods are not ideally accurate for star sensor.

As the new generation of star sensor is more similar to ordinary camera, we consider using camera calibration methods in computer vision for calibration. There are many literatures working on ordinary camera calibration [13–16]. Literature [13] presented that calibration can be done very efficiently by observing a calibration object whose geometry in 3D space is known with very good precision. Literature [14] proposed a method to calibrate a camera, which consists of a closed-form solution and followed by a nonlinear refinement. But this method requires the 3D information of the points. Literature [15] calibrated from an analysis of point matches between the images with a rotating camera. Literature [16] analyses the lens distortion in close-range camera calibration. These methods calibrate more parameters than star sensor, such as the principal point offset, focal length (on column and row direction) and lens distortion, which could increase the accuracy. These methods of ordinary camera are not completely suitable for star sensor; i.e., the data from star sensor cannot be used directly. But we use them in our paper by a suitable way.

The calibration data from ground-based real night sky observation are confined by many conditions [8]. For simplicity, we choose to simulate stars in laboratory. We establish the laboratory calibration by using a collimator, a two-dimensional pan-tilt-zoom (PTZ) and a CCD star sensor. The collimator is used to simulate stars in the laboratory, and the CCD star sensor is mounted on the PTZ. This paper presents a method to calibrate the principal point offset, focal length, radial distortion, tangential distortion and installation error of star sensor, which is based on nonlinear optimal method estimation, taking into account installation error and calibration methods of ordinary camera. The work aims to provide a simple and available solution for calibration issue of star sensor without having high accurate or expensive devices.

This paper is organized as follows. In Sect. 2, the general calibration model using least-square method is described. The advanced model that considers installation error is discussed in Sect. 3. To verify the performance of the proposed method, extensive experiments are performed in Sect. 4. Finally, conclusions are represented in Sect. 5.

2 The star sensor calibration method

Traditional star sensor calibration method only calibrates the principal point offset and focal length of star sensors. We take account of ordinary camera calibration methods for star sensor calibration [14, 16]. The star sensor calibration method consists of three parts. The first is an approximate pinhole camera model that neglects all lens distortion. The second is to take radial distortion and tangential distortion into account. Finally, we use a nonlinear refinement to get results.

2.1 Distortion-free calibration model

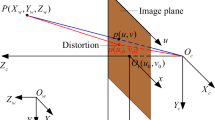
Stars are considered as infinitely far objects that focus on the focal plane of an imager. The simulated star is denoted by P. The star sensor coordinate system is denoted by o-xyz. Ideal PTZ coordinate system is the same as o-xyz. The origin of the o-xyz is the optical center of the star sensor, and the z axis coincides with its optical axis. The x axis and y axis coincide with the vertical and horizontal rotation axes of PTZ. The image plane c-uv, which corresponds to the image sensing array, is assumed to be parallel to the xoy plane and at a distance f to the origin, where f represents the (effective) focal length of the star sensor. The world coordinate system is denoted by O-XYZ. X axis and Y axis coincide with the vertical and horizontal rotation axes in case both rotation angles are both 0°, which called PTZ initial state. All the coordinate system in this paper is right hand. Figure 1 shows the relationship among o-xyz, O-XYZ and c-uv.

Fig. 1
figure 1

Ideal pinhole camera model and star sensor coordinates

Full size image

As previously discussed, the calibration method of ideal pinhole camera model requires the coordinates of P in O-XYZ. However, to determine PTZ initial state, it can be optional to the coordinates of P in O-XYZ nonunique. The ordinary way is to determine PTZ initial state in the knowable position so that the coordinates of P in O-XYZ can be unique.

One of the special positions is that let the Z axis through the point P, as illustrated in Fig. 1. Let \({\mathbf{P}}_{w} = [0,0,c]^{T} ,c \approx \infty\) represent the coordinates in O-XYZ, so point P is in the Z axis. \({\mathbf{P}}_{i} = [x_{i} ,y_{i} ,z_{i} ]^{T}\) represent the corresponding coordinates in o-xyz. \({\mathbf{I}}_{i}^{\prime } = (u_{i}^{\prime } ,v_{i}^{\prime } )\) represent the nonobservable, distortion-free image coordinates in c-uv. \({\mathbf{I}}_{i} = [u_{i} ,v_{i} ]^{T}\) is the observable distortion image coordinates in c-uv. We have \({\mathbf{I}}_{i}^{\prime } = {\mathbf{I}}_{i}\) on the distortion-free camera model. The transformation between O-XYZ and o-xyz is presented as follows:

$${\mathbf{P}}_{i} = {\mathbf{R}}_{i} \cdot {\mathbf{P}}_{w} ,$$
(1)

where \({\mathbf{R}}_{i}\) is a 3 × 3 rotation matrix from O-XYZ to o-xyz. And \({\mathbf{R}}_{i}\) is defined by the PTZ horizontal rotation angle \(\theta_{i}\) and vertical rotation angle \(\varphi_{i}\):

$${\mathbf{R}}_{i} = \left( {\begin{array}{*{20}c} {\cos (\theta_{i} )} \hfill & 0 \hfill & { - \sin (\theta_{i} )} \hfill \\ {\sin (\theta_{i} )\sin (\varphi_{i} )} \hfill & { - \cos (\varphi_{i} )} \hfill & {\cos (\theta_{i} )\sin (\varphi_{i} )} \hfill \\ {\sin (\theta_{i} )\cos (\varphi_{i} )} \hfill & {\sin (\varphi_{i} )} \hfill & {\cos (\theta_{i} )\cos (\varphi_{i} )} \hfill \\ \end{array} } \right)$$
(2)

According to geometric properties of optical imaging, as illustrated in Fig. 1, we have the following:

$$z_{i} \left( {\begin{array}{*{20}c} {u_{i} } \hfill \\ {v_{i} } \hfill \\ 1 \hfill \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {f_{u} } \hfill & 0 \hfill & {u_{0} } \hfill \\ 0 \hfill & {f_{v} } \hfill & {v_{0} } \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {x_{i} } \hfill \\ {y_{i} } \hfill \\ {z_{i} } \hfill \\ \end{array} } \right) = {\mathbf{K}} \cdot {\mathbf{P}}_{i}$$
(3)

where \((u_{0} ,v_{0} )\) represents the principal point of the image plane (i.e., the intersection of the image plane with the optical axis), u and v axes are chosen parallel to x and y axis, f u represents the focal length on the column direction, and f v represents the focal length on the row direction. In the traditional calibration model, \(f_{u} = f_{v}\).

Combining (1)–(3) leads to the following expressions that relate pixel position, the world coordinates and the various parameters to be calibrated.

$$\left\{ {\begin{array}{*{20}c} {\cos (\theta_{i} )\cos (\varphi_{i} )u_{i} = - \sin (\theta_{i} )f_{u} { + }u_{0} \cos (\theta_{i} )\cos (\varphi_{i} )} \hfill \\ {\cos (\theta_{i} )\cos (\varphi_{i} )v_{i} = f_{v} \cos (\theta_{i} )\sin (\varphi_{i} ){ + }v_{0} \cos (\theta_{i} )\cos (\varphi_{i} )} \hfill \\ \end{array} } \right.$$
(4)

Given the star P’s pixel locations \([u_{i} ,v_{i} ]^{T}\) in n image, above calibration problem can be easily solved by direct linear transformation (DLT) [17] and linear least-squares method (LSM) [18].

2.2 Lens distortion model

Up to now, we have not considered lens distortion of a star sensor. However, a star sensor usually exhibits significant lens distortion such as radial distortion, tangential distortion and thin prism distortion [19]. Referred to the literature [20, 21], it is shown that the distortion is totally dominated by the radial and tangential components, and any more elaborated modeling would cause numerical instability. However, it also has been found that higher-order lens distortion calibration model is feasible and potentially significant for wide angle lens or enough calibration data points [22, 23]. In this section, the first two terms of radial distortion and tangential distortion are considered (Fig. 2).

Fig. 2
figure 2

Radial and tangential distortion

Full size image

Let \({\mathbf{I}}_{i}^{\prime } = (u_{i}^{\prime } ,v_{i}^{\prime } )\) be the ideal (nonobservable distortion-free) pixel image coordinates, and \({\mathbf{I}}_{i} = [u_{i} ,v_{i} ]^{T}\) be the corresponding real observed image coordinates. Similarly, \((\bar{x}_{i}^{\prime } ,\bar{y}_{i}^{\prime } )\) and \((\bar{x}_{i} ,\bar{y}_{i} )\) are the ideal (distortion-free) and real (distorted) normalized image coordinates. We have the following:

$$\left( {\begin{array}{*{20}c} {\bar{x}_{i}^{\prime } } \hfill \\ {\bar{y}_{i}^{\prime } } \hfill \\ \end{array} } \right){ = }\left( {\begin{array}{*{20}c} {x_{c} /z_{c} } \hfill \\ {y_{c} /z_{c} } \hfill \\ \end{array} } \right)$$
(5)

According to [24], we come up with our lens distortion model taking radial and tangential distortion into account:

$$\begin{aligned} \tilde{u}_{i} & = f_{u} [\bar{x}_{i}^{\prime } \left( {1{ + }k_{1} \rho_{i}^{2} { + }k_{2} \rho_{i}^{4} } \right) \\ & \quad { + }2k_{3} \bar{x}_{i}^{\prime } \bar{y}_{i}^{\prime } { + }k_{4} (\rho_{i}^{2} { + }2\bar{x}_{i}^{\prime 2} )] + u_{0} \\ \tilde{v}_{i} & = f_{v} [\bar{y}_{i}^{\prime } \left( {1{ + }k_{1} \rho_{i}^{2} { + }k_{2} \rho_{i}^{4} } \right) \\ & \quad { + }k_{3} (\rho_{i}^{2} { + }2\bar{y}_{i}^{\prime 2} ) { + }2k_{4} \bar{x}_{i}^{\prime } \bar{y}_{i}^{\prime } ] + v_{0} \\ \end{aligned}$$
(6)

where \((\tilde{u}_{i} ,\tilde{v}_{i} )\) is the image coordinates get from Eq. (6), and \(\rho_{i} = \sqrt {\bar{x}_{i}^{\prime 2} + \bar{y}_{i}^{\prime 2} }\). k 1 k 2 are coefficients for radial distortion, and k 3 k 4 are coefficients for tangential distortion.

Given the star P’s pixel locations \([u_{i} ,v_{i} ]^{T}\) in n image, we stack all equations (6) together to obtain in total 2n equations, or in matrix form as

$${\mathbf{D}} \cdot {\mathbf{k = d}},$$
(7)

where

$${\mathbf{D}} = \left( {\begin{array}{*{20}c} {f_{u} \bar{x}_{1}^{\prime } \rho_{1}^{2} } \hfill & {f_{u} \bar{x}_{1}^{\prime } \rho_{1}^{4} } \hfill & {2f_{u} \bar{x}_{1}^{\prime } \bar{y}_{1}^{\prime } } \hfill & {f_{u} (\rho_{1}^{2} { + }2\bar{x}_{1}^{\prime 2} )} \hfill \\ {f_{v} \bar{y}_{1}^{\prime } \rho_{1}^{2} } \hfill & {f_{v} \bar{y}_{1}^{\prime } \rho_{1}^{4} } \hfill & {f_{v} (\rho_{1}^{2} { + }2\bar{y}_{1}^{\prime 2} )} \hfill & {2f_{v} \bar{x}_{1}^{\prime } \bar{y}_{1}^{\prime } } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {f_{u} \bar{x}_{n}^{\prime } \rho_{n}^{2} } \hfill & {f_{u} \bar{x}_{n}^{\prime } \rho_{n}^{4} } \hfill & {2f_{u} \bar{x}_{n}^{\prime } \bar{y}_{n}^{\prime } } \hfill & {f_{u} (\rho_{n}^{2} { + }2\bar{x}_{n}^{\prime 2} )} \hfill \\ {f_{v} \bar{y}_{n}^{\prime } \rho_{n}^{2} } \hfill & {f_{v} \bar{y}_{n}^{\prime } \rho_{n}^{4} } \hfill & {f_{v} (\rho_{n}^{2} { + }2\bar{y}_{n}^{\prime 2} )} \hfill & {2f_{v} \bar{x}_{n}^{\prime } \bar{y}_{n}^{\prime } } \hfill \\ \end{array} } \right)$$
$${\mathbf{k}} = [k_{1} ,k_{2} ,k_{3} ,k_{4} ]^{T}$$
$${\mathbf{d}}{ = }\left( {\begin{array}{*{20}c} {u_{1} - (f_{u} \bar{x}_{1}^{\prime } + u_{0} )} \hfill \\ {v_{1} - (f_{v} \bar{y}_{1}^{\prime } + v_{0} )} \hfill \\ \vdots \hfill \\ {u_{n} - (f_{v} \bar{x}_{n}^{\prime } + u_{0} )} \hfill \\ {u_{n} - (f_{v} \bar{y}_{n}^{\prime } + v_{0} )} \hfill \\ \end{array} } \right)$$

The linear least-squares solution is given by

$${\mathbf{k}} = ({\mathbf{D}}^{T} \cdot {\mathbf{D}} )^{ - 1} \cdot {\mathbf{D}}^{T} \cdot {\mathbf{d}}$$
(8)

2.3 Maximum likelihood estimation

The above solution is obtained through minimizing an algebraic distance which is not sufficiently accurate. We can refine it through maximum likelihood inference.

Given the star P’s pixel locations \([u_{i} ,v_{i} ]^{T}\) in n image. Assume that the image points are corrupted by independent and identically distributed noise. The maximum likelihood estimate can be obtained by minimizing the following functional:

$$\mathop {\hbox{min} }\limits_{{{\mathbf{X}} \in R^{8} }} \sum\limits_{\text{i = 1}}^{n} {\left\| { (u_{i} ,v_{i} )^{T} - (\tilde{u}_{i} ,\tilde{v}_{i} )^{T} } \right\|^{2} }$$
(9)

where \({\mathbf{X}} = \left( {f_{u} ,f_{v} ,u_{0} ,v_{0} ,k_{1} ,k_{2} ,k_{3} ,k_{4} } \right)^{T} \in R^{8}\) are the parameters to be calibrated.

Minimizing (9) is a nonlinear minimization problem, which is solved with the Levenberg–Marquardt algorithm [25]. It requires an initial guess of X which can be obtained using Eqs. (4) and (8).

3 Dealing with installation error

Installation error is generated in the process of the installation, use and calibration. The main sources of installation error are the installation of PTZ initial status, the installation of the PTZ and the installation of the CCD. In order to get the more accurate calibration result, the installation error is modeled in the installation process.

3.1 The installation error of PTZ initial status

On the assumption of \({\mathbf{P}}_{w} = [0,0,c]^{T} ,\,c \approx \infty\), we have a prerequisite that the point P must be on the Z axis, which usually cannot be satisfied in actual operation. There is installation error between point P and Z axis. Figure 3 illustrates the installation error.

Fig. 3
figure 3

Installation error of collimator

Full size image

Let OP be the Z′ axis and establish a right-handed coordinate system O-X′Y′Z. Let X′ and Y′ axes are very close to the X and Y axes. O-XYZ is the world coordinate system illustrated in Fig. 1. \({\mathbf{P}}_{w}^{\prime } = [0,0,c]^{T} ,c \approx \infty\) represent the coordinates in O-X′Y′Z′. The transformation between O-XYZ and O-X′Y′Z′ is presented as follows:

$${\mathbf{P}}_{w} = {\mathbf{R}}_{e} \cdot {\mathbf{P}}_{w}^{\prime } ,$$
(10)

where \({\mathbf{R}}_{e}\) is a 3 × 3 rotation matrix from O-X′Y′Z′ to O-XYZ, which is regarded as installation error of PTZ initial status. And \({\mathbf{R}}_{e}\) is defined by rotation angles a and b. The rotation angles a and b are both small.

$${\mathbf{R}}_{e} = \left( {\begin{array}{*{20}c} {\cos (a)} \hfill & {\sin (a)\sin (b)} \hfill & {\sin (a)\cos (b)} \hfill \\ 0 \hfill & { -\cos (b)} \hfill & {\sin (b)} \hfill \\ { -\sin (a)} \hfill & {\cos (a)\sin (b)} \hfill & {\cos (a)\cos (b)} \hfill \\ \end{array} } \right)$$
(11)

Combining (10) and (11) leads to the following expressions that the point P in O-XYZ:

$${\mathbf{P}}_{w} = \left( {\begin{array}{*{20}c} {\sin (a)\cos (b)} \hfill \\ {\sin (b)} \hfill \\ {\cos (a)\cos (b)} \hfill \\ \end{array} } \right)c$$
(12)

Furthermore, if we define O-X′Y′Z as right-handed coordinate system, then Z′ axis through the point P and O-XYZ is the PTZ initial status coordinate system. The transformation between O-XYZ and O-X′Y′Z′ is also presented by \({\mathbf{R}}_{e}\), and rotation angles a and b can be bigger. However, by determining PTZ initial status, we can uniquely represent \({\mathbf{P}}_{w}\) by \({\mathbf{R}}_{e}\). We do not need to determine PTZ initial state in the knowable position to obtain \({\mathbf{P}}_{w}\).

For simplicity sake, we regard \({\mathbf{R}}_{e}\) as installation error of PTZ initial status. We can set the initial guess of a and b to 0.

3.2 The installation error of PTZ

In actual operation, the star sensor is not exactly mounted on the PTZ. There are small offset angles between the star sensor and PTZ.

Let the PTZ coordinate system be denoted by o-X i Y i Z i . The X i axis and Y i axis coincide with the vertical and horizontal rotation axis of PTZ. o-xyz is the star sensor coordinate system illustrated in Fig. 1. α, β, γ represent those small offset angles. Figure 4 illustrates the installation error.

Fig. 4
figure 4

Installation error of PTZ

Full size image

The transformation between o-X i Y i Z i and o-xyz is presented as follows:

$$\left( {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right) = R_{c} \left( {\begin{array}{*{20}c} {X_{i} } \\ {Y_{i} } \\ {Z_{i} } \\ \end{array} } \right),$$
(13)

where \({\mathbf{R}}_{c}\) is a 3 × 3 rotation matrix from o-X i Y i Z i to o-xyz, which is regarded as installation error of PTZ. And \({\mathbf{R}}_{e}\) is defined by α, β, γ. The rotation angles α, β, and γ are small.

$${\mathbf{R}}_{e} = \left( {\begin{array}{*{20}c} {\cos (\gamma )} \hfill & {\sin (\gamma )} \hfill & 0 \hfill \\ { - \sin (\gamma )} \hfill & {\cos (\gamma )} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\cos (\beta )} \hfill & {\sin (\beta )} \hfill \\ 0 \hfill & { - \sin (\beta )} \hfill & {\cos (\beta )} \hfill \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {\cos (\alpha )} \hfill & 0 \hfill & { - \sin (\alpha )} \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill \\ {\sin (\alpha )} \hfill & 0 \hfill & {\cos (\alpha )} \hfill \\ \end{array} } \right)$$
(14)

3.3 The installation error of CCD

Ideal CCD plane is that the two image axes are perpendicular. But actually, the two image axes are not strictly perpendicular to each other. We let f s denote the parameter describing the skewness of the two image axes [14]. The orthogonal error of two image axes is due to a variety of factors [20], such as slight hardware timing mismatch between image acquisition hardware and camera scanning hardware, or defects produced in CCDs’ manufacture process. The skew is hardly caused by CCD defects so that most literatures consider f s  = 0 in camera calibration. However, all the installation processes of CCD will cause errors more or less. Referring to literature [26], the skew caused by hardware timing mismatch is very important in camera calibration. The effect of f s is approximate to the installation error of CCD. So, we redefined the intrinsic parameters matrix K as:

$${\mathbf{K}} = \left( {\begin{array}{*{20}c} {f_{u} } & {f_{s} } & {u_{0} } \\ 0 & {f_{v} } & {v_{0} } \\ 0 & 0 & 1 \\ \end{array} } \right)$$
(15)

where Eq. (3) is the special case of f s  = 0, which represents the ideal case of CCD plane.

3.4 Complete star sensors model

Combining (1), (2), (12), (13) and (15) leads to the complete image model

$$z_{i} \left( {\begin{array}{*{20}c} {u_{i} } \hfill \\ {v_{i} } \hfill \\ 1 \hfill \\ \end{array} } \right) = {\mathbf{K}} \cdot {\mathbf{R}}_{c} \cdot {\mathbf{R}}_{i} \cdot {\mathbf{R}}_{e} \cdot \left( {\begin{array}{*{20}c} 0 \hfill \\ 0 \hfill \\ c \hfill \\ \end{array} } \right)$$
(16)

Additionally, considering the lens distortion model (6), combining (9) and (16) leads to the complete star sensor calibration model in this paper:

$$\mathop {\hbox{min} }\limits_{{{\mathbf{X}} \in R^{14} }} \sum\limits_{\text{i = 1}}^{n} {\left\| { (u_{i} ,v_{i} )^{T} - (\tilde{u}_{i} ,\tilde{v}_{i} )^{T} } \right\|^{2} }$$
(17)

where \({\mathbf{X}}{ = }\left( {f_{u} ,f_{v} ,f_{s} ,u_{0} ,v_{0} ,k_{1} ,k_{2} ,k_{3} ,k_{4} ,a,b,\alpha ,\beta ,\gamma } \right)^{T} \in R^{14}\) are the parameters to be calibrated, \(f_{u} ,f_{v} ,f_{s} ,u_{0} ,v_{0}\) are the intrinsic parameters of star sensor, \(k_{1} ,k_{2} ,k_{3} ,k_{4}\) are the coefficients for lens distortion, and \(a,b,\alpha ,\beta ,\gamma\) are the parameters describing the installation errors.

Similarly, minimizing (17) is a nonlinear minimization problem, which is solved by the Levenberg–Marquardt algorithm. It requires an initial guess of X which can be obtained using Eqs. (4) and (8). \(a,b,\alpha ,\beta ,\gamma\) can be simply stetted to 0.

4 Experiments and results

4.1 Configuration and data

The laboratory calibration environment configuration is illustrated in Fig. 5.

Fig. 5
figure 5

Laboratory calibration environment configuration

Full size image

The collimator is used to simulate stars, and the CCD star sensor is mounted on the PTZ [27, 28]. PTZ is panned with a horizontal rotation angle and tilted with a vertical rotation angle to set a star sensor attitude. The zoom control of PTZ is not useful in our work. We take some images of simulate star P under different orientations by turning PTZ rotation of a certain angle and obtain the star P’s pixel locations in n images. The schematic data acquisition process is illustrated in Fig. 6. The regular gridded field of view samples is not only convenient for operation, but also suit for rectangular characteristic of CCD array. In addition, stars are evenly distributed over the image plane that will benefit for lens distortion calibration.

Fig. 6
figure 6

Data acquisition process schematic

Full size image

4.2 Result and analysis

The proposed method has been tested on both computer simulated data and real data. The nonlinear refining within the Levenberg–Marquardt algorithm takes 20–30 iterations to converge.

4.2.1 Computer simulations

In the computer simulation experiment, the star centroid estimation error in pixel needs to be considered. Generally speaking, systematic error of star centroid estimation in pixel is related with the intensity distribution of star image and the star centroid estimation methods. The star signal distribution can be expressed as Gaussian distribution in most situations [29, 30], and Gaussian function is a very good centroid estimation method for dealing with the normal range of stellar images [31, 32]. As a result, the star centroid estimation error can be considered as Gaussian distribution in most cases. In our experiment, we add a Gaussian noise distribution to the exact position of star image centroid in the pixel to simulate real case.

The simulated star sensor has the following properties which are shown in the first row of Table 1. The star sensor has a wider FOV of 60° × 60°, and the size of image plane is 1,024 pixel × 1,024 pixel. We totally obtain 900 data points, every 2° with one point obtained. The following experiments in this chapter are based on above basic configuration. According to different experimental requirements, only part of these conditions will be changed.

Table 1 Relative error of estimated result versus the noise level of the image points
Full size table
4.2.1.1 Performance with respect to noise level

This experiment investigates the performance with respect to noise level. Gaussian noise with 0 mean and σ standard deviation is added to the exact position of star image centroid in the pixel. The estimated star sensor parameters are then compared with the exact values. The noise level is varied from 0 pixels to 8 pixels. We perform 30 independent trials, and the results shown in Table 1 are the average. The first row (noise) is the noise level measured in pixel. The subsequent rows show the relative error for each estimated parameter. As we can see from Table 1, almost all the errors are small. The errors in \(f_{u} ,f_{v} ,f_{s} ,u_{0} ,v_{0}\) are lower than 1 pixel, and the errors in \(k_{1} ,k_{2} ,k_{3} ,k_{4}\) are lower than 0.001. But the errors in \(a,b,\alpha ,\beta ,\gamma\) are large. The main reason is that \(a,b,\alpha ,\beta ,\gamma\) are too small to be effected by noise. Furthermore, we can see that errors increase linearly with the noise level.

Additionally, we measure the root of mean square distance (RMS) between the estimated star sensor parameters and the exact values. As we can see from Fig. 7, although the value of error is small, lower than 1 in σ = 8, RMS slowly increases linearly with the noise level. The conclusion is the same as Table 1. Therefore, if we want to obtain the better result, it is better to decrease the noise.

Fig. 7
figure 7

RMS versus noise level

Full size image
4.2.1.2 Performance with respect to the number of data points

This experiment investigates the performance with respect to the number of data points. The number of data points is varied from 1(1 × 1) to 324(18 × 18). For each number, 50 trials of independent data points and independent noise with mean 0 and standard deviation 0.5 pixels are conducted. We measure the RMS between the estimated star sensor parameters and the exact values. As we can see from Fig. 8, RMS decreases when more data points are used. From 4 to 64, the RMS decreases significantly. The result shows that we need at least about 64 data points to obtain accurate calibration result.

Fig. 8
figure 8

RMS versus the number of data points

Full size image
4.2.1.3 Performance with respect to the size of FOV

This experiment investigates the performance with respect to the size of FOV (more precisely, the wider FOV). We vary the size of FOV from 10° × 10° to 90° × 90°, and let 900 data points be evenly distributed over the image plane for each FOV size. For each size, 50 trials of independent data points and independent noise with mean 0 and standard deviation 0.5 pixels are conducted. We measure the RMS between the estimated star sensor parameters and the exact values. As we can see from Fig. 9, RMS decreases when wider FOV star sensor is used. The RMS decreases significantly from 10° × 10° to 16° × 16°, and it decreases gently from 16° × 16° to 38° × 38°. The main reason is that small FOV size star sensor is more severely affected by noise [33]. The result shows that our calibration method is feasible for wider FOV star sensor calibration and is better used for 38° × 38° or larger. It means that the wider the size of FOV, the more precise the calibration result.

Fig. 9
figure 9

RMS versus the size of FOV

Full size image

4.2.2 Real data

We use a star sensor of 42° × 42° FOV to calibrate. We provide the result with real data set consisting of 81 data points; every 4° obtain one point. The size of the entire image plane is 1,024 pixel × 1,024 pixel.

4.2.2.1 Model comparisons

According to the investigation of chapter “Performance with respect to the number of data points,” we applied our method [Eq. (17)] to three quarters of total data points (61 points) to do parameter calibration, and the rest of points (21 points) for testing the errors. As a comparison, we also applied traditional method [9], laboratory method [12] and initial method [Eq. (9)] to the data set. The results are shown in Table 2. For last two configurations, two columns are given. The first column (initial) is the estimation of the closed-form solution. The second column (final) is the maximum likelihood estimation (MLE). The last row (RMS) displays the root of mean square distances between testing points and projected ones measured in pixel. The row (MD) before RMS displays the maximum distances between testing points and projected ones measured in pixel. Our method improves considerably these measures with the results of MD = 0.728 pixel and RMS = 0.379 pixel. (1 pixel is equal to 0.041° in 42° × 42° FOV). The accuracy of our method is 0.030° in MD and 0.015° in RMS, which has the same level as the traditional star sensor calibration methods [8]. Though the accuracy of literatures [10, 11] is higher than our method, their methods require high-precision calibration devices to guarantee the high calibration precision. Our calibration method is a simple and available solution for calibration issue of star sensor without having high accurate and expensive devices.

Table 2 Model comparisons result with real data
Full size table

The reason for inconsistency for k 1, k 2 between the closed-form solution and the MLE is that for the closed-form solution, star sensor intrinsic parameters are estimated assuming no distortion, and the predicted outer points lie closer to the image center than the detected ones. The subsequent distortion estimation tries to spread the outer points and increase the scale in order to reduce the distances, although the distortion shape does not correspond to the real distortion. The MLE finally recovers the correct distortion shape.

The value of the skew parameter is no significant from 0. Indeed, f s  = 5.534 with f u  = 1,401.805 corresponds to 89.773°, for the angle between the two image axes. This means that the two image axes of CCD plane are not strictly perpendicular to each other. The primary cause is the rough accuracy caused by cheaper mechanical components and manual operation. Therefore, skew angle of 0.227° (f s  = 5.534) is in a reasonable range.

The value of the aspect ratio f u /f v is equal to 0.9977. It is therefore very close to 1; i.e., the pixels are square.

4.2.2.2 Analysis on the direction of error vector

The error vector between data points and projected ones can be used to verify the calibration result. If the direction of the vector is with regularity, it means the calibration result is poor. Otherwise, if it is random, the result is feasible. Figure 10 illustrates the error vector. (a) is the error vector, with scale 100, drawn in Cartesian coordinate system. (b) is the error vector drawn in polar coordinate system. We can see that the error vector is not larger than 1 pixel. To observe error vector in polar coordinate system (b), we can found that their direction is obviously random. Therefore, the calibration result is feasible.

Fig. 10
figure 10

Error vector between data points and projected ones (a cartesian coordinate, b polar coordinate)

Full size image
4.2.2.3 Cross-validation

In order to further investigate the stability of our star sensor calibration method, we have applied the model to the data to do cross-validation. We evenly divide data set into four parts, numbered 1, 2, 3 and 4. We use 3 of the sub-data to do parameter calibration and the other one to test the error. All combinations of 4 sub-data have been used. The results are shown in Table 3, where the first column (123), for example, displays the calibration result with the sub-data 1, 2 and 3, and the MD and RMS are used for the sub-data 4. The last two columns display the mean and sample deviation of the four sets of results. The sample deviations for all parameters are quite small, which implies that the model is quite stable.

Table 3 Cross-validation of the calibration results
Full size table

5 Conclusion

In this paper, we present a simple and available method to calibrate the principal point, focal length, radial distortion, tangential distortion and installation error of star sensor in laboratory, and without having high accurate or expensive devices. The calibration model takes the ordinary camera calibration methods and installation error into account. The installation error is modeled by combination of three typical effects: the installation of PTZ initial status, PTZ and CCD, which result in six parameters. The proposed procedure consists of a closed-form solution, followed by a nonlinear refining based on maximum likelihood criterion. Both computer simulation and real data have been used to validate our method, and very good results have been obtained.

Need to note here that our method in this paper does not take into account more comprehensive factor. We can carry on further study in the following work.