Characteristics of tilted and off-axis partially coherent beams reflected back by a cat-eye optical lens in atmospheric turbulence

Abstract

In this paper, taking the tilted and off-axis partially coherent beams as the active detection laser beams, the characteristics of the active detection laser beams reflected back by a cat-eye optical lens in atmospheric turbulence are studied analytically and numerically. The analytical expressions for the centroid position deviation γ, the average intensity, the mean-squared beam width and the far-field divergence angle at the receiver plane are derived. It is found that tilted and off-axis active detection laser beams cannot be reflected back by a cat-eye optical lens in the direction of the source. The absolute deviation $\left| \gamma \right|$ decreases as the beam coherence decreases. Therefore, partially coherent beams are more suitable as active detection laser beams than fully coherent ones. In addition, $\left| \gamma \right|$ decreases greatly due to the aperture effect, and the influence of turbulence on $\left| \gamma \right|$ is not monotonic. On the other hand, the influence of the beam coherence and the atmospheric turbulence on the average intensity, the mean-squared beam width and the far-field divergence angle at the receiver plane is also examined, and some interesting results are obtained. The results obtained in this paper are very useful for applications of the active laser detection.

1 Introduction

The phenomenon that a light beam is reflected back by an optical system in the direction of the source is called the cat-eye effect. Two types of the optical system have this function, i.e., the cat’s eye reflector and the cat-eye optical lens. The cat’s eye reflector has many advantages such as diffraction limit [1] and low sensitivity to the direction of the incident light beam because it is well designed [2]. The cat’s eye reflector is a cooperative target in applications. The cat’s eye reflector is widely used in laser tracking interferometer systems [3], adjustment-free lasers [2, 4], micro-displacement measurements [5] and free space optical communications [6–8].

On the other hand, the optical lens used in the photoelectric equipment has a detector fixed on its focal plane, and the optical lens is called the cat-eye optical lens. By using the active laser detection technique based on the theory of cat-eye effect of optical lens, a much longer detection distance and a higher orientation precision can be obtained than by using passive detection technique [9, 10]. Active laser detection based on the cat-eye effect is a new type of technique used in laser weapons, and the key technology is to describe the reflection characteristics of optical targets exactly. The active detection laser beams may be tilted and off-axis because the cat-eye optical lens is a non-cooperative target in applications. The intensity distribution of tilted and off-axis Gaussian beams propagating through a cat-eye optical lens was studied in [11]. Some of optical lenses used in photoelectric equipment have the center shelter. The propagation properties of Gaussian beams through a cat-eye optical lens with center shelter were studied in [12]. In addition, in order to obtain more information about the target, the diffraction and interference characteristics of the cat-eye reflected light beams are important for applications in recognition technique [13]. However, in these studies [11–13], active detection laser beams are fully coherent Gaussian beams, and the atmospheric turbulence is not considered.

The atmospheric turbulence effect and the aperture effect of cat-eye optical lens cannot be neglected because active detection laser beams propagate a long distance in atmospheric turbulence. The propagation of laser beams through atmospheric turbulence is a topic that has been considerable theoretical and practical interest for a long time [14–29]. The partially coherent beams are often encountered in practice. It has been demonstrated that partially coherent beams are less sensitive to the effect of turbulence than fully coherent ones [16–18]. Then, some important questions arise: Are partially coherent beams more suitable as active detection laser beams than fully coherent beams? Can active detection laser beams still be reflected back in the direction of the source if active detection laser beams are tilted and off-axis? What are the effects of the turbulence and the apertures on the characteristics of active detection laser beams?

In this paper, taking the tilted and off-axis partially coherent beam as the active detection laser beam, we answer the questions mentioned above. In Sect. 2, we study whether tilted and off-axis partially coherent beams can be reflected back by a cat-eye optical lens in the direction of the source in turbulence, where the centroid position deviation is taken as the criterion. For the perpendicular incidence case, the average intensity, the mean-squared beam width and the far-field divergence angle of partially coherent beams reflected back by a cat-eye optical lens in turbulence at the receiver plane are examined in Sect. 3. In Sect. 4, the main results obtained in this paper are summarized.

2 Centroid position deviation

2.1 Theoretical model and formulae

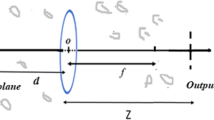
The propagation of tilted and off-axis partially coherent beams reflected back by a cat-eye optical lens in atmospheric turbulence can be illustrated by Fig. 1. The optical system shown in Fig. 1 is symmetrical about the detector because the laser beam is reflected by the detector. It is assumed that there is no atmospheric turbulence between the two lenses with the same focal length f. The law of laser beams propagating through a cat-eye optical lens in the y direction is the same as that in the x direction. For simplicity, in this paper, only one dimension along x direction is considered (see Fig. 1). The hard-edge apertures 1 and 3 with full width h ₁ oriented along the x-axis are located just before lens 1 and after lens 2, respectively. The hard-edge aperture 2 with full width h ₂ oriented along the x-axis is just located at the detector plane. δ is the distance between the detector and the focal plane, which is called the defocus parameter. L is the distance between the source plane and the lens 1, which is also the distance between the lens 2 and the receiver plane. θ is the tilted angle of the active detection laser beam, and D = tanθ is called the tilted parameter. $\Updelta x^{\prime }$ and Δx are the off-axis parameters of the active detection laser beam at the source plane and the lens 1 plane, respectively, and $\Updelta x^{\prime } = \Updelta x - DL$.

Fig. 1

Schematic illustration of tilted and off-axis detection laser beams reflected back by a cat-eye optical lens in atmospheric turbulence

It can be seen that the laser beam propagation through a cat-eye optical lens consists of four steps, i.e., the first step: the propagation through atmospheric turbulence over a distance L; the second step: the propagation through the apertured lens 1 and free space over a distance f + δ; the third step: the propagation through the aperture 2 and free space over a distance f + δ and the lens 2; the fourth step: the propagation through an aperture 3 and atmospheric turbulence over a distance L. The transfer matrixes of the four propagation steps are given by

$$\left[ {\begin{array}{*{20}c} {a_{1} } & {b_{1} } \\ {c_{1} } & {d_{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & L \\ 0 & 1 \\ \end{array} } \right],$$

(1)

$$\left[ {\begin{array}{*{20}c} {a_{2} } & {b_{2} } \\ {c_{2} } & {d_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - {\delta \mathord{\left/ {\vphantom {\delta f}} \right. \kern-0pt} f}} & {f + \delta } \\ { - {1 \mathord{\left/ {\vphantom {1 f}} \right. \kern-0pt} f}} & 1 \\ \end{array} } \right],$$

(2)

$$\left[ {\begin{array}{*{20}c} {a_{3} } & {b_{3} } \\ {c_{3} } & {d_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & {f + \delta } \\ { - {1 \mathord{\left/ {\vphantom {1 f}} \right. \kern-0pt} f}} & { - {\delta \mathord{\left/ {\vphantom {\delta f}} \right. \kern-0pt} f}} \\ \end{array} } \right],$$

(3)

$$\left[ {\begin{array}{*{20}c} {a_{4} } & {b_{4} } \\ {c_{4} } & {d_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & L \\ 0 & 1 \\ \end{array} } \right].$$

(4)

In this paper, the Gaussian Schell-model (GSM) beam is taken as a typical example of partially coherent beams. An analytical treatment of the aberrations is proposed by using the decomposition of the phase of the beam in terms of the Zernike polynomials [30]. For one dimension case, the cross-spectral density function of tilted and off-axis GSM beams at the source plane can be written as

$$W_{0} \left( {x_{1}^{\prime } ,x_{2}^{\prime } ,0} \right) = { \exp }\left[ { - ikD\left( {x_{1}^{\prime } -x_{2}^{\prime } } \right)} \right]{ \exp }\left[ { - \frac{{\left( {x_{1}^{\prime } -\Updelta x^{\prime } } \right)^{2} + \left( {x_{2}^{\prime } -\Updelta x^{\prime } } \right)^{2} }}{{w_{0}^{2} }} - \frac{{\left( {x_{1}^{\prime } -x_{2}^{\prime } } \right)^{2} }}{{2\sigma_{0}^{2} }}} \right],$$

(5)

where $x^{\prime}_{1}$ and $x_{2}^{\prime }$ are the transverse coordinates along the x direction at the source plane, k = 2π/λ is the wavenumber (λ is the wavelength), w ₀ and σ₀ are the waist width and the coherence length at the source plane, respectively.

Based on the extended Huygens-Fresnel principle, the cross-spectral density function of tilted and off-axis GSM beams after the first propagation step is expressed as [14]

$$\begin{aligned} W_{1} (x_{11} ,x_{21} ,z) & = \frac{1}{{\lambda b_{1} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {W_{0} \left( {x_{1}^{\prime } ,x_{2}^{\prime } ,0} \right){ \exp }\left\{ { - \frac{i\pi }{{\lambda b_{1} }}\left[ {a_{1} \left( {x_{1}^{\prime 2} - x_{2}^{\prime 2} } \right) - 2\left( {x_{11} x_{1}^{\prime } - x_{21} x_{2}^{\prime } } \right)} \right.} \right.} } \\ & \quad \left. {\left. { + {{d}}_{1} \left( {x_{11}^{2} - x_{21}^{2} } \right)} \right]} \right\}\left\langle {{ \exp }\left[ {\psi^{*} \left( {x_{11} ,x_{1}^{\prime } ,z} \right) + \psi \left( {x_{21} ,x_{2}^{\prime } ,z} \right)} \right]} \right\rangle_{m} {\text{d}}x_{1}^{\prime } {\text{d}}x_{2}^{\prime } , \\ \end{aligned}$$

(6)

where x ₁₁ and x ₂₁ are the transverse coordinates along the x direction at the aperture 1 plane, $\psi (x,x^{\prime } ,z)$ is the complex phase function that depends on properties of the turbulence medium. < > _m denotes average over the ensemble of the turbulent medium, and [31]

$$\left\langle {\exp \left[ {\psi^{*} \left( {x_{11} ,x_{1}^{\prime } ,z} \right) + \psi \left( {x_{21} ,x_{2}^{\prime } ,z} \right)} \right]} \right\rangle_{m} \cong { \exp }\left[ { - \frac{{\left( {x_{1}^{\prime } - x_{2}^{\prime } } \right)^{2} + \left( {x_{1}^{\prime } - x_{2}^{\prime } } \right)(x_{11} - x_{21} ) + (x_{11} - x_{21} )^{2} }}{{\rho_{0}^{2} }}} \right],$$

(7)

where $\rho_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - {3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}}$ is the spatial coherence radius of a spherical wave propagating in turbulence, and $C_{n}^{2}$ is the refraction index structure constant which describes how strong the turbulence is. Here, we employed the Kolmogorov spectrum and a quadratic approximation of the 5/3 power law for Rytov’s phase structure function. This quadratic approximation has been shown to be a good approximation for the second-order moment [31–33].

On substituting from Eqs. (5) and (7) into Eq. (6), and recalling the integral formula

$$\int\limits_{ - \infty }^{ + \infty } {{ \exp }( - s^{2} x^{2} \pm qx){\text{d}}x} = \frac{\sqrt \pi }{s}\exp \left( {\frac{{q^{2} }}{{4s^{2} }}} \right)\quad (s > 0),$$

(8)

and performing the integration with respect to $x_{1}^{\prime }$ and $x_{2}^{\prime }$ in Eq. (6), we obtain

$$\begin{aligned} W_{1} (x_{11} ,x_{21} ,z) & = \frac{\pi }{{\lambda b_{1} }}\exp (g_{1} )\exp \left[ { - \frac{{i\pi d_{1} }}{{\lambda b_{1} }}\left( {x_{11}^{2} - x_{21}^{2} } \right)} \right]\frac{1}{{p_{1} p_{2} }}\exp \left[ {r_{3} x_{11}^{2} + t_{1} x_{11} } \right. \\ & \quad \left. { + r_{2} x_{21}^{2} + s_{1} x_{21} + r_{1} x_{11} x_{21} + {{(r_{4} x_{21} + u_{1} x_{11} + v_{1} )^{2} } \mathord{\left/ {\vphantom {{(r_{4} x_{21} + u_{1} x_{11} + v_{1} )^{2} } {4p_{2}^{2} }}} \right. \kern-0pt} {4p_{2}^{2} }}} \right], \\ \end{aligned}$$

(9)

where

$$p_{1}^{2} = \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\alpha^{2} w_{0}^{2} }} + \frac{{i\pi a_{1} }}{{\lambda b_{1} }},$$

(10)

$$p_{2}^{2} = \frac{1}{{w_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\alpha^{2} w_{0}^{2} }} - \frac{{i\pi a_{1} }}{{\lambda b_{1} }} - \frac{1}{{p_{1}^{2} \rho_{0}^{4} }} - \frac{1}{{4p_{1}^{2} \alpha^{4} w_{0}^{4} }} - \frac{1}{{p_{1}^{2} \rho_{0}^{2} \alpha^{2} w_{0}^{2} }},$$

(11)

$$g_{1} = - \frac{{D^{2} k^{2} }}{{4p_{1}^{2} }} + \frac{{\Updelta x^{\prime 2} }}{{p_{1}^{2} w_{0}^{4} }} - \frac{{i\Updelta x^{\prime } Dk}}{{p_{1}^{2} w_{0}^{2} }} - \frac{{2\Updelta x^{\prime 2} }}{{w_{0}^{2} }},$$

(12)

$$r_{2} = \frac{1}{{4p_{1}^{2} \rho_{0}^{4} }} - \frac{1}{{\rho_{0}^{2} }},\quad r_{3} = r_{2} - \frac{{\pi^{2} }}{{b_{1}^{2} p_{1}^{2} \lambda^{2} }} - \frac{i\pi }{{b_{1} p_{1}^{2} \lambda \rho_{0}^{2} }},$$

(13)

$$s_{1} = \frac{{\Updelta x^{\prime } }}{{p_{1}^{2} w_{0}^{2} \rho_{0}^{2} }} - \frac{iDk}{{2p_{1}^{2} \rho_{0}^{2} }},\quad t_{1} = \frac{Dk\pi }{{b_{1} p_{1}^{2} \lambda }} + \frac{{2i\Updelta x^{\prime } \pi }}{{b_{1} p_{1}^{2} \lambda w_{0}^{2} }} - s_{1} ,$$

(14)

$$r_{1} = - \frac{1}{{2p_{1}^{2} \rho_{0}^{4} }} + \frac{2}{{\rho_{0}^{2} }} + \frac{i\pi }{{b_{1} p_{1}^{2} \lambda \rho_{0}^{2} }},$$

(15)

$$r_{4} = - \frac{2i\pi }{{b_{1} \lambda }} + \frac{1}{{p_{1}^{2} \rho_{0}^{4} }} - \frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2p_{1}^{2} \rho_{0}^{2} \alpha^{2} w_{0}^{2} }},$$

(16)

$$u_{1} = \frac{2i\pi }{{b_{1} p_{1}^{2} \lambda \rho_{0}^{2} }} + \frac{i\pi }{{b_{1} p_{1}^{2} \lambda \alpha^{2} w_{0}^{2} }} - \frac{1}{{p_{1}^{2} \rho_{0}^{4} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{1}{{2p_{1}^{2} \alpha^{2} w_{0}^{2} \rho_{0}^{2} }},$$

(17)

$$v_{1} = iDk + \frac{{2\Updelta x^{\prime } }}{{w_{0}^{2} }} - \frac{iDk}{{p_{1}^{2} \rho_{0}^{2} }} + \frac{{2\Updelta x^{\prime } }}{{p_{1}^{2} w_{0}^{2} \rho_{0}^{2} }} - \frac{iDk}{{2p_{1}^{2} \alpha^{2} w_{0}^{2} }} + \frac{{\Updelta x^{\prime } }}{{p_{1}^{2} w_{0}^{2} \alpha^{2} w_{0}^{2} }},$$

(18)

with α = σ ₀/w ₀ being called the beam coherence parameter.

After the second propagation step, the cross-spectral density function is given by [14]

$$\begin{aligned} W_{2} (x_{12} ,x_{22} ,z) & = \frac{1}{{\lambda b_{2} }}\exp \left[ { - \frac{{i\pi d_{2} }}{{\lambda b_{2} }}\left( {x_{12}^{2} - x_{22}^{2} } \right)} \right]\int\limits_{{ - {{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } 2}} \right. \kern-0pt} 2}}} {\int\limits_{{ - {{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } 2}} \right. \kern-0pt} 2}}} {W_{1} (x_{11} ,x_{21} ,z)} } \\ & \quad \times { \exp }\left\{ { - \frac{i\pi }{{\lambda b_{2} }}\left[ {a_{2} \left( {x_{11}^{2} - x_{21}^{2} } \right) - 2(x_{11} x_{12} - x_{21} x_{22} )} \right]} \right\}{\text{d}}x_{11} {\text{d}}x_{21} . \\ \end{aligned}$$

(19)

where x ₁₂ and x ₂₂ are the transverse coordinates along the x direction at the aperture 2 plane.

The window function of the aperture is described by the rectangular function of form

$$f\left( x \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {\left| x \right|} \\ \end{array} \le {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} \\ {\begin{array}{*{20}c} 0 & {\left| x \right| > {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} \\ \end{array} } \\ \end{array} } \right.,$$

(20)

where h is the full width of the aperture.

f(x) can be expanded into a finite sum of complex-valued Gaussian functions [34]

$$f(x) = \sum\limits_{i = 1}^{M} {F_{i} \exp } \left[ { - {{4G_{i} x^{2} } \mathord{\left/ {\vphantom {{4G_{i} x^{2} } {h^{2} }}} \right. \kern-0pt} {h^{2} }}} \right],$$

(21)

where the coefficients F _i , G _i and the number M are evaluated by a computation fitting given by Wen and Breazeale in Tab. 1 of Ref. [34] for M = 10 and are omitted here. According to Wen and Breazeale, the method of the finite expansion of the aperture function is applicable to the Fraunhofer and Fresnel regions except for the extreme near field (<0.12 times the Fresnel distance) [34]. Bearing this point in mind, Eq. (19) can be rewritten as

$$\begin{aligned} W_{2} (x_{12} ,x_{22} ,z) & = \frac{1}{{\lambda b_{2} }}\exp \left[ { - \frac{{i\pi d_{2} }}{{\lambda b_{2} }}\left( {x_{12}^{2} - x_{22}^{2} } \right)} \right]\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {f_{{i_{11} }} (x_{11} )f_{{i_{21} }}^{ * } (x_{21} )W_{1} (x_{11} ,x_{21} ,z)} } \\ & \quad \times { \exp }\left\{ { - \frac{i\pi }{{\lambda b_{2} }}\left[ {a_{2} \left( {x_{11}^{2} - x_{21}^{2} } \right) - 2(x_{11} x_{12} - x_{21} x_{22} )} \right]} \right\}{\text{d}}x_{11} {\text{d}}x_{21} . \\ \end{aligned}$$

(22)

On substituting from Eqs. (9) and (21) into Eq. (22), recalling the integral formula (8) and performing the integration with respect to x ₁₁ and x ₂₁ in Eq. (22) in turn, we obtain

$$\begin{aligned} W_{2} (x_{12} ,x_{22} ,z) & = \left( {\frac{\pi }{\lambda }} \right)^{2} \frac{1}{{b{}_{1}b_{2} }}\exp (g_{1} + g_{2} )\exp \left[ { - \frac{{i\pi d_{2} }}{{\lambda b_{2} }}\left( {x_{12}^{2} - x_{22}^{2} } \right)} \right]\frac{1}{{p_{1} p_{2} }}\sum\limits_{{i_{11} = 1}}^{10} {\sum\limits_{{i_{21} = 1}}^{10} {\frac{{F_{{i_{11} }} F_{{i_{21} }}^{ * } }}{{p_{3} p_{4} }}} } \\ & \quad \times { \exp }\left[ {\left( {\frac{i\pi }{{\lambda b_{2} p_{3} }}} \right)^{2} x_{12}^{2} + t_{2} x_{12} - \frac{1}{{4p_{4}^{2} }}\left( {\frac{2i\pi }{{\lambda b_{2} }}x_{22} - u_{2} x_{12} - v_{2} } \right)^{2} } \right], \\ \end{aligned}$$

(23)

where

$$p_{3}^{2} = \frac{{4G_{{i_{11} }} }}{{h_{1}^{2} }} + \frac{{ia_{2} \pi }}{{b_{2} \lambda }} + \frac{{id_{1} \pi }}{{b_{1} \lambda }} - \frac{{u_{1}^{2} }}{{4p_{2}^{2} }} - r_{3} ,\quad u_{2} = \frac{{i\pi r_{1} }}{{b_{2} p_{3}^{2} \lambda }} + \frac{{i\pi r_{4} u_{1} }}{{2b_{2} p_{2}^{2} p_{3}^{2} \lambda }},$$

(24)

$$p_{4}^{2} = \frac{{4G_{{_{{i_{21} }} }}^{ * } }}{{h_{1}^{2} }} - \frac{{ia_{2} \pi }}{{b_{2} \lambda }} - \frac{{id_{1} \pi }}{{b_{1} \lambda }} - \frac{{r_{4}^{2} }}{{4p_{2}^{2} }} - \frac{{r_{1}^{2} }}{{4p_{3}^{2} }} - \frac{{r_{1} r_{4} u_{1} }}{{4p_{2}^{2} p_{3}^{2} }} - \frac{{r_{4}^{2} u_{1}^{2} }}{{16p_{2}^{4} p_{3}^{2} }} - r_{2} ,$$

(25)

$$g_{2} = \frac{{v_{1}^{2} }}{{4p_{2}^{2} }} + \frac{{t_{1}^{2} }}{{4p_{3}^{2} }} + \frac{{v_{1} t_{1} u_{1} }}{{4p_{2}^{2} p_{3}^{2} }} + \frac{{v_{1}^{2} u_{1}^{2} }}{{16p_{2}^{4} p_{3}^{2} }},\quad t_{2} = \frac{{i\pi t_{1} }}{{b_{2} p_{3}^{2} \lambda }} + \frac{{iv_{1} u_{1} \pi }}{{2b_{2} p_{2}^{2} p_{3}^{2} \lambda }},$$

(26)

$$v_{2} = \frac{{v_{1} r_{4} }}{{2p_{2}^{2} }} + \frac{{r_{1} t_{1} }}{{2p_{3}^{2} }} + \frac{{r_{1} v_{1} u_{1} }}{{4p_{2}^{2} p_{3}^{2} }} + \frac{{r_{4} t{}_{1}u_{1} }}{{4p_{2}^{2} p_{3}^{2} }} + \frac{{v_{1} r_{4} u_{1}^{2} }}{{8p_{2}^{4} p_{3}^{2} }} + s_{1} .$$

(27)

Similarly, after the third propagation step, the cross-spectral density function can be derived as

$$\begin{aligned} W_{3} (x_{13} ,x_{23} ,z) & = \left( {\frac{\pi }{\lambda }} \right)^{3} \frac{1}{{b_{1} b_{2} b{}_{3}}}\exp (g_{1} + g_{2} + g_{3} )\exp \left[ { - \frac{{i\pi d_{3} }}{{\lambda b_{3} }}\left( {x_{13}^{2} - x_{23}^{2} } \right)} \right]\frac{1}{{p_{1} p_{2} }}\sum\limits_{{i_{11} = 1}}^{10} {\sum\limits_{{i_{21} = 1}}^{10} {\frac{{F_{{i_{11} }} F_{{i_{21} }}^{{^{ * } }} }}{{p_{3} p_{4} }}} } \\ & \quad \times \sum\limits_{{i_{12} = 1}}^{10} {\sum\limits_{{i_{22} = 1}}^{10} {\frac{{F_{{i_{12} }} F_{{i_{22} }}^{{^{ * } }} }}{{p_{5} p_{6} }}} } \exp \left[ {\left( {\frac{i\pi }{{\lambda b_{3} p_{5} }}} \right)} \right.^{2} x_{13}^{2} + t_{3} x_{13} \left. { - \frac{1}{{4p_{6}^{2} }}\left( {\frac{2i\pi }{{\lambda b_{3} }}x_{23} - u_{3} x_{13} - v_{3} } \right)^{2} } \right], \\ \end{aligned}$$

(28)

where x ₁₃ and x ₂₃ are the transverse coordinates along the x direction at the aperture 3 plane, and

$$p_{5}^{2} = \frac{{4G_{{i_{12} }} }}{{h_{2}^{2} }} + \frac{{\pi^{2} }}{{b_{2}^{2} p_{3}^{2} \lambda^{2} }} + \frac{{ia_{3} \pi }}{{b_{3} \lambda }} + \frac{{id_{2} \pi }}{{b_{2} \lambda }} - \frac{{u_{2}^{2} }}{{4p_{4}^{2} }},$$

(29)

$$p_{6}^{2} = \frac{{4G_{{i_{22} }}^{ * } }}{{h_{2}^{2} }} + \frac{{\pi^{2} }}{{b_{2}^{2} p_{4}^{2} \lambda^{2} }} - \frac{{ia_{3} \pi }}{{b_{3} \lambda }} - \frac{{id_{2} \pi }}{{b_{2} \lambda }} + \frac{{\pi^{2} u_{2}^{2} }}{{4b_{2}^{2} p_{4}^{4} p_{5}^{2} \lambda^{2} }},$$

(30)

$$g_{3} = \frac{{v_{2}^{2} }}{{4p_{4}^{2} }} + \frac{{t_{2}^{2} }}{{4p_{5}^{2} }} + \frac{{v_{2} t_{2} u_{2} }}{{4p_{4}^{2} p_{5}^{2} }} + \frac{{v_{2}^{2} u_{2}^{2} }}{{16p_{4}^{4} p_{5}^{2} }},\quad t_{3} = \frac{{i\pi t_{2} }}{{b_{3} p_{5}^{2} \lambda }} + \frac{{iv_{2} u_{2} \pi }}{{2b_{3} p_{4}^{2} p_{5}^{2} \lambda }},$$

(31)

$$u_{3} = \frac{{\pi^{2} u_{2} }}{{b_{2} b_{3} p_{4}^{2} p_{5}^{2} \lambda^{2} }},\quad v_{3} = - \frac{{iv_{2} \pi }}{{b_{2} p_{4}^{2} \lambda }} - \frac{{i\pi t_{2} u_{2} }}{{2b_{2} p_{4}^{2} p_{5}^{2} \lambda }} - \frac{{iv_{2} u_{2}^{2} \pi }}{{4b_{2} p_{4}^{4} p_{5}^{2} \lambda }},$$

(32)

After the last propagation step, the cross-spectral density function of tilted and off-axis GSM beams at the receiver plane is expressed as [14]

$$\begin{aligned} W_{4} (x_{14} ,x_{24} ,z) & = \frac{1}{{\lambda b_{4} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {f_{{i_{13} }} (x_{13} )f_{{i_{23} }}^{ * } (x_{23} )W_{3} (x_{13} ,x_{23} ,z)\exp \left\{ { - \frac{i\pi }{{\lambda b_{4} }}\left[ {a_{4} \left( {x_{13}^{2} - x_{23}^{2} } \right) - 2(x_{14} x_{13} - x_{24} x_{23} )} \right.} \right.} } \\ & \quad \left. {\left. { + d_{4} \left( {x_{14}^{2} - x_{24}^{2} } \right)} \right]} \right\}\left\langle {\exp [\psi * (x_{14} ,x_{13} ,z) + \psi (x_{24} ,x_{23} ,z)]} \right\rangle_{m} {\text{d}}x_{13} {\text{d}}x_{23} . \\ \end{aligned}$$

(33)

where x ₁₄ and x ₂₄ are the transverse coordinates along the x direction at the receiver plane. Letting x ₁₄ = x ₂₄ = x, substituting from Eqs. (7), (21) and (28) into Eq. (33), recalling the integral formula (8), and performing the integration with respect to x ₁₃ and x ₂₃ in Eq. (33) in turn, we obtain the average intensity of tilted and off-axis GSM beams reflected back by a cat-eye optical lens in atmospheric turbulence at the receiver plane, i.e.,

$$\begin{aligned} \left\langle {I(x,L)} \right\rangle & = \left( {\frac{\pi }{\lambda }} \right)^{4} \frac{1}{{b_{1} b_{2} b_{3} b_{4} }}\frac{1}{{p_{1} p_{2} }}\sum\limits_{{i_{11} = 1}}^{10} {\sum\limits_{{i_{21} = 1}}^{10} {\frac{{F_{{i_{11} }} F_{{i_{21} }}^{ * } }}{{p_{3} p_{4} }}} } \sum\limits_{{i_{12} = 1}}^{10} {\sum\limits_{{i_{22} }}^{10} {\frac{{F_{{i_{12} }} F_{{i_{22} }}^{ * } }}{{p_{5} p_{6} }}} } \sum\limits_{{i_{13} = 1}}^{10} {\sum\limits_{{i_{23} = 1}}^{10} {\frac{{F_{{i_{13} }} F_{{i_{23} }}^{ * } }}{{p_{7} p_{8} }}} } \\ & \quad \times { \exp }(g_{1} + g_{2} + g_{3} + g_{4} )\exp \left[ {\left( {\frac{{u_{4}^{2} }}{{4p_{8}^{2} }} - \frac{{\pi^{2} }}{{b_{4}^{2} p_{7}^{2} \lambda^{2} }}} \right)x^{2} + \left( {t_{4} + \frac{{u_{4} v_{4} }}{{2p_{8}^{2} }}} \right)x + \frac{{v_{4}^{2} }}{{4p_{8}^{2} }}} \right], \\ \end{aligned}$$

(34)

where

$$p_{7}^{2} = \frac{{4G_{{i_{13} }} }}{{h_{1}^{2} }} + \frac{{\pi^{2} }}{{b_{3}^{2} p_{5}^{2} \lambda^{2} }} + \frac{{ia_{4} \pi }}{{b_{4} \lambda }} + \frac{{id_{3} \pi }}{{b_{3} \lambda }} + \frac{1}{{\rho_{0}^{2} }} - \frac{{u_{3}^{2} }}{{4p_{6}^{2} }},$$

(35)

$$p_{8}^{2} = \frac{{4G_{{_{{i_{23} }} }}^{ * } }}{{h_{1}^{2} }} + \frac{{\pi^{2} }}{{b_{2}^{2} p_{6}^{2} \lambda^{2} }} - \frac{{ia_{4} \pi }}{{b_{4} \lambda }} - \frac{{id_{3} \pi }}{{b_{3} \lambda }} + \frac{1}{{\rho_{0}^{2} }} + \frac{{\pi^{2} u_{3}^{2} }}{{4b_{3}^{2} p_{6}^{4} p_{7}^{2} \lambda^{2} }} + \frac{{i\pi u_{3} }}{{b_{3} p_{6}^{2} p_{7}^{2} \rho_{0}^{2} \lambda }} - \frac{1}{{p_{7}^{2} \rho_{0}^{4} }},$$

(36)

$$g_{4} = \frac{{v_{3}^{2} }}{{4p_{6}^{2} }} + \frac{{t_{3}^{2} }}{{4p_{7}^{2} }} + \frac{{v_{3} t_{3} u_{3} }}{{4p_{6}^{2} p_{7}^{2} }} + \frac{{v_{3}^{2} u_{3}^{2} }}{{16p_{6}^{4} p_{7}^{2} }},$$

(37)

$$t_{4} = \frac{{i\pi t_{3} }}{{b_{4} p_{7}^{2} \lambda }} + \frac{{iv_{3} u_{3} \pi }}{{2b_{4} p_{6}^{2} p_{7}^{2} \lambda }},\quad u_{4} = \frac{{\pi^{2} u_{3} }}{{b_{3} b_{4} p_{6}^{2} p_{7}^{2} \lambda^{2} }} + \frac{2i\pi }{{b_{4} p_{7}^{2} \rho_{0}^{2} \lambda }} - \frac{2i\pi }{{b_{4} \lambda }},$$

(38)

$$v_{4} = - \frac{{iv_{3} \pi }}{{b_{3} p_{6}^{2} \lambda }} - \frac{{i\pi t_{3} u_{3} }}{{2b_{3} p_{6}^{2} p_{7}^{2} \lambda }} - \frac{{iv_{3} u_{3}^{2} \pi }}{{4b_{3} p_{6}^{4} p_{7}^{2} \lambda }} + \frac{{t_{3} }}{{p_{7}^{2} \rho_{0}^{2} }} + \frac{{v_{3} u_{3} }}{{2p_{6}^{2} p_{7}^{2} \rho_{0}^{2} }}.$$

(39)

The intensity moments are very useful for characterizing laser beams. The first-order intensity moment denotes the centroid position of laser beams, which is defined as [35]

$$\bar{x} = {{\int\limits_{ - \infty }^{ + \infty } {x\left\langle {I(x,z)} \right\rangle {\text{d}}x} } \mathord{\left/ {\vphantom {{\int\limits_{ - \infty }^{ + \infty } {x\left\langle {I(x,z)} \right\rangle {\text{d}}x} } {\int\limits_{ - \infty }^{ + \infty } {\left\langle {I(x,z)} \right\rangle } }}} \right. \kern-0pt} {\int\limits_{ - \infty }^{ + \infty } {\left\langle {I(x,z)} \right\rangle } }}{\text{ d}}x.$$

(40)

On substituting from Eq. (34) into Eq. (40), after very tedious but straightforward integral calculations, we obtain the centroid position of tilted and off-axis GSM beams reflected back by a cat-eye optical lens in atmospheric turbulence at the receiver plane, which is given by

$$\bar{x}_{2} = {{\sum\limits_{{i_{11} = 1}}^{10} {\sum\limits_{{i_{21} = 1}}^{10} {\sum\limits_{{i_{12} = 1}}^{10} {\sum\limits_{{i_{22} = 1}}^{10} {\sum\limits_{{i_{13} = 1}}^{10} {\sum\limits_{{i_{23} = 1}}^{10} {s_{2} s_{3} } } } } } } } \mathord{\left/ {\vphantom {{\sum\limits_{{i_{11} = 1}}^{10} {\sum\limits_{{i_{21} = 1}}^{10} {\sum\limits_{{i_{12} = 1}}^{10} {\sum\limits_{{i_{22} = 1}}^{10} {\sum\limits_{{i_{13} = 1}}^{10} {\sum\limits_{{i_{23} = 1}}^{10} {s_{2} s_{3} } } } } } } } {\sum\limits_{{i_{11} = 1}}^{10} {\sum\limits_{{i_{21} = 1}}^{10} {\sum\limits_{{i_{12} = 1}}^{10} {\sum\limits_{{i_{22} = 1}}^{10} {\sum\limits_{{i_{13} = 1}}^{10} {\sum\limits_{{i_{23} = 1}}^{10} {s_{2} s_{4} } } } } } } }}} \right. \kern-0pt} {\sum\limits_{{i_{11} = 1}}^{10} {\sum\limits_{{i_{21} = 1}}^{10} {\sum\limits_{{i_{12} = 1}}^{10} {\sum\limits_{{i_{22} = 1}}^{10} {\sum\limits_{{i_{13} = 1}}^{10} {\sum\limits_{{i_{23} = 1}}^{10} {s_{2} s_{4} } } } } } } }},$$

(41)

where

$$s_{3} = \frac{{t_{4} }}{2} + \frac{{v_{4} u_{4} }}{{4p_{8}^{2} }},\quad s_{4} = \frac{{\pi^{2} }}{{b_{4}^{2} p_{7}^{2} \lambda^{2} }} - \frac{{u_{4}^{2} }}{{4p_{8}^{2} }},$$

(42)

$$s_{2} = \frac{{F_{{i_{11} }} F_{{i_{21} }}^{ * } F_{{i_{12} }} F_{{i_{22} }}^{ * } F_{{i_{13} }} F_{{i_{23} }}^{ * } }}{{p_{3} p_{4} p_{5} p_{6} }}\sqrt {\frac{\pi }{{s_{4} }}} \exp \left( {g_{1} + g_{2} + g_{3} + g_{4} + \frac{{v_{4}^{2} }}{{4p_{8}^{2} }} + \frac{{s_{3}^{2} }}{{s_{4} }}} \right).$$

(43)

In this paper, the centroid position deviation γ is defined as the difference between the centroid position of laser beams at the receiver plane and that at the source plane, i.e.,

$$\gamma = \bar{x}_{2} - \bar{x}_{1} ,$$

(44)

where $\bar{x}_{1}$ is the centroid position of the incident beams expressed by Eq. (5), and $\bar{x}_{1}$ can be derived as $\bar{x}_{1} = \Updelta x - DL$. It is clear that a larger $\left| \gamma \right|$ means the larger deviation from the direction of the source, and active detection laser beams can be reflected back by a cat-eye optical lens in the direction of the source when γ = 0.

For the unapertured case (i.e., $h_{1} \to \infty$ and $h_{2} \to \infty$), Eq. (44) reduces to

$$\gamma = {{2(Df - \Updelta x)(f^{2} + f\delta - L\delta )} \mathord{\left/ {\vphantom {{2(Df - \Updelta x)(f^{2} + f\delta - L\delta )} {f^{2} }}} \right. \kern-0pt} {f^{2} }}.$$

(45)

From Eq. (45), some interesting results for the unapertured case can be obtained, which are given as follows:

• 1. Τhe centroid position deviation γ is independent of the beam coherence parameter α and the refraction index structure constant $C_{n}^{2}$, which is quite different from the behavior for the apertured case.

• 2. For D = 0 case, Eq. (45) reduces to γ = −2Δx(f ² + fδ − Lδ)/f ², i.e., $\left| \gamma \right|$ increases with increasing $\left| {\Updelta x} \right|$. For $\Updelta x = 0$ case, Eq. (45) reduces to γ = 2D(f + δ − Lδ/f), i.e., $\left| \gamma \right|$ increases with increasing $\left| D \right|$.

• 3. For Df = Δx or Lδ = f(f + δ) case, Eq. (45) reduces to γ = 0, i.e., active detection laser beams can be reflected back by a cat-eye optical lens in the direction of the source.

When D = Δx = 0, we have γ = 0 both for apertured and unapertured cases. The physical reason is that the intensity distributions at the source and receiver planes are all symmetrical about the x-axis, i.e., $\bar{x}_{1} = \bar{x}_{2} = 0$.

It is mentioned that we check the lengthy formulas provided in this paper by comparing them to some of the results already existing in the literature. For example, when D = 0, Δx = 0, α = ∞ and $C_{n}^{2} = 0$, Eq. (34) in this paper can reduce to Eq. (14) in [12] when the center shelter ratio ε = 0. In addition, for the unapertured case (i.e., $h_{1} \to \infty$ and $h_{2} \to \infty$), we derive independently the expression for the centroid position deviation γ, which is the same as Eq. (45) in this paper.

2.2 Numerical calculation results and analysis

Some numerical calculations are performed to illustrate changes of the centroid position deviation γ, please see Figs. 2, 3, 4, 5, where w ₀ = 1 mm, λ = 1.06 μm, f = 500 mm, δ = 0 and L = 2 km are taken. Figures 2 and 3 give changes of γ versus the tilted parameter D for the Δx = 0 case, and Figs. 4 and 5 show changes of γ versus the off-axis parameter Δx for the D = 0 case. When Δx = 0, it can be seen that the absolute deviation $\left| \gamma \right|$ increases with increasing $\left| D \right|$ (see Figs. 2 and 3). On the other hand, $\left| \gamma \right|$ increases with increasing $\left| {\Updelta x} \right|$ when D = 0 (see Figs. 4 and 5). Comparing Fig. 2b with Fig. 2a, we can see that $\left| \gamma \right|$ decreases greatly due to aperture effect, and this result can also be obtained in Fig. 4. Figure 3 shows that $\left| \gamma \right|$ increases with increasing the beam coherence parameter α both in turbulence and in absence of turbulence, which can also be seen in Fig. 5. $\left| \gamma \right|$ decreases when the turbulence strength is not strong enough (see Figs. 3a, 5a), while $\left| \gamma \right|$ increases when the turbulence strength is strong enough (see Figs. 3b, 5b). In addition, Fig. 3b shows that there exist several cross-points between two lines (see the two lines for the small α = 0.3 in strong turbulence and for the large α = 2 in absence of turbulence, respectively). It means that $\left| \gamma \right|$ of active detection laser beams with small α in the strong turbulence may be smaller than that with large α in absence of turbulence.

Fig. 2

Changes of the centroid position deviation γ versus the tilted parameter D. Δx = 0, $C_{n}^{2} = 0$, α = 0.8

Fig. 3

Changes of the centroid position deviation γ versus the tilted parameter D. Δx = 0, h ₁ = 150 mm, h ₂ = 20 mm

Fig. 4

Changes of the centroid position deviation γ versus the off-axis parameter Δx. D = 0, $C_{n}^{2} = 0$, α = 0.8

Fig. 5

Changes of the centroid position deviation γ versus the off-axis parameter Δx. D = 0, h ₁ = 150 mm, h ₂ = 20 mm

The physical explanations of the main results obtained above are given as follows. The field deviation from the z-axis increases as $\left| D \right|$ and $\left| {\Updelta x} \right|$ increase, which causes $\left| \gamma \right|$ to increase because of increase in $\left| D \right|$ and $\left| {\Updelta x} \right|$. On the other hand, the field deviation from the z-axis decreases due to the apertures, which results in decrease in $\left| \gamma \right|$ for the apertured case.

Figure 6 gives the average intensity distributions at the receiver plane for α = 0.3 and 2 at different propagation distances. Firstly, it shows that the unsymmetricalness of the average intensity distribution is larger for α = 2 than that for α = 0.3. Secondly, the beam spreading is larger for α = 2 than that for α = 0.3 when the different propagation distance is not small (see Fig. 6c, d), which is quite different from the behavior for the apertured case. These are the physical reasons why $\left| \gamma \right|$ increases with increasing the beam coherence parameter α.

Fig. 6

Average intensity distributions <I(x, L)> at the receiver plane versus x. Δx = 0.05 m, D = 0, h ₁ = 150 mm, h ₂ = 20 mm

3 Other characteristics

From Sect. 2, we see that active detection laser beams can be reflected back by a cat-eye optical lens in the direction of the source exactly for the perpendicular incidence case (i.e., D = Δx = 0). In this section, we examine some other characteristics (e.g., the average intensity, the mean-squared beam width and the far-field divergence angle) at the receiver plane when D = Δx = 0.

3.1 Average intensity

When D = Δx = 0, Eq. (34) reduces to

$$\left\langle {I(x,L)} \right\rangle = \left( {\frac{\pi }{\lambda }} \right)^{4} \frac{1}{{b_{1} b_{2} b_{3} b_{4} }}\frac{1}{{p_{1} p_{2} }}\sum\limits_{{i_{11} = 1}}^{10} {\sum\limits_{{i_{21} = 1}}^{10} {\frac{{F_{{i_{11} }} F_{{i_{21} }}^{ * } }}{{p_{3} p_{4} }}} } \sum\limits_{{i_{12} = 1}}^{10} {\sum\limits_{{i_{22} }}^{10} {\frac{{F_{{i_{12} }} F_{{i_{22} }}^{ * } }}{{p_{5} p_{6} }}} } \sum\limits_{{i_{13} = 1}}^{10} {\sum\limits_{{i_{23} = 1}}^{10} {\frac{{F_{{i_{13} }} F_{{i_{23} }}^{ * } }}{{p_{7} p_{8} }}} } \exp \left[ {\left( {\frac{{u_{4}^{2} }}{{4p_{8}^{2} }} - \frac{{\pi^{2} }}{{b_{4}^{2} p_{7}^{2} \lambda^{2} }}} \right)x^{2} } \right],$$

(46)

By using Eq. (46), the on-axis average intensity distributions at the receiver plane versus the defocus parameter δ for α = 0.3 and 2 are plotted in Fig. 7a, b, respectively. It can be seen that for the small positive defocus case, the on-axis average intensity reaches its maximum, e.g., δ = 51 μm in Fig. 7a, b, which is independent of α and $C_{n}^{2}$.

Fig. 7

On-axis average intensity distributions <I(0, L)> at the receiver plane versus the defocus parameter δ. w ₀ = 1 mm, λ = 1.06 μm, Δx = D = 0, h ₁ = 100 mm, h ₂ = 20 mm, f = 500 mm, L = 5 km

The average intensity distributions at the receiver plane versus x for α = 0.3 and 2 are depicted in Fig. 8a, b, respectively, where δ = 0 and δ = 51 μm are considered. It is clear that for δ = 51 μm, the average intensity is larger and the beam width is smaller than those for δ = 0 in absence of turbulence. However, the two average intensity distributions are close to each other due to turbulence. Comparing Fig. 8b with Fig. 8a, we can see that the main difference of the average intensity distribution between α = 2 and 0.3 is that the average intensity is larger for α = 2 than that for α = 0.3.

Fig. 8

Average intensity distributions <I(x, L)> at the receiver plane versus x. w ₀ = 1 mm, λ = 1.06 μm, Δx = D = 0, h ₁ = 100 mm, h ₂ = 20 mm, f = 500 mm, L = 5 km

In order to illustrate the influence of turbulence on the characteristics, the Strehl ratio and the parameter β are adopted. The Strehl ratio is defined as S _R  = I _max/I _0max, where I _max and I _0max are the maximum intensity in turbulence and in absence of turbulence, respectively. The smaller S _R is, the more the maximum intensity is affected by turbulence. The parameter β is defined as β = w _turb/w _free, where w _turb and w _free are the mean-squared beam width in turbulence and in absence of turbulence, respectively. The smaller β means the beam spreading is less affected by turbulence. The values of S _R and β are given in Fig. 8. It can be seen that the influence of α on the beam spreading and the maximum intensity can be neglected nearly, but for δ = 51 μm, the beam spreading and the maximum intensity are more affected by turbulence than those for δ = 0. The propagation of laser beams in atmospheric turbulence is affected by two mechanisms, i.e., free space diffraction and atmospheric turbulence. It is known that turbulence results in the beam spreading and the intensity decreasing. In physical, the effects of turbulence are masked by the larger spreading and the smaller intensity in free space [16]. From Fig. 8, it can be seen that in free space, the beam spreading is smaller and the intensity is larger when δ = 51 μm than those when δ = 0. This is the physical reason why laser beams are more sensitive to turbulence when δ = 51 μm than those when δ = 0.

3.2 Mean-squared beam width and far-field divergence angle

The second-order moment represents the beam width, which is called the mean-squared beam width and is defined as [35]

$$w^{2} (L) = {{4\int\limits_{ - \infty }^{ + \infty } {x^{2} \left\langle {I(x,L)} \right\rangle {\text{d}}x} } \mathord{\left/ {\vphantom {{4\int\limits_{ - \infty }^{ + \infty } {x^{2} \left\langle {I(x,L)} \right\rangle {\text{d}}x} } {\int\limits_{ - \infty }^{ + \infty } {\left\langle {I(x,L)} \right\rangle {\text{d}}x} }}} \right. \kern-0pt} {\int\limits_{ - \infty }^{ + \infty } {\left\langle {I(x,L)} \right\rangle {\text{d}}x} }}.$$

(47)

On substituting from Eq. (46) into Eq. (47) and after tedious but straightforward integration, we can obtain the mean-squared beam width of GSM beams reflected back by a cat-eye optical lens in atmospheric turbulence at the receiver plane, i.e.,

$$w^{2} (L) = A + BL + CL^{2} + FL^{{{{16} \mathord{\left/ {\vphantom {{16} 5}} \right. \kern-0pt} 5}}} ,$$

(48)

where

$$A = \frac{{2\sum\nolimits_{{i_{11} = 1}}^{10} {\sum\nolimits_{{i_{21} = 1}}^{10} {\sum\nolimits_{{i_{12} = 1}}^{10} {\sum\nolimits_{{i_{22} = 1}}^{10} {\sum\nolimits_{{i_{13} = 1}}^{10} {\sum\nolimits_{{i_{23} = 1}}^{10} {D_{2} } } } } } } }}{{\sum\nolimits_{{i_{11} = 1}}^{10} {\sum\nolimits_{{i_{21} = 1}}^{10} {\sum\nolimits_{{i_{12} = 1}}^{10} {\sum\nolimits_{{i_{22} = 1}}^{10} {\sum\nolimits_{{i_{13} = 1}}^{10} {\sum\nolimits_{{i_{23} = 1}}^{10} {D_{2} s_{5} } } } } } } }},\quad B = - \frac{{2i\sum\nolimits_{{i_{11} = 1}}^{10} {\sum\nolimits_{{i_{21} = 1}}^{10} {\sum\nolimits_{{i_{12} = 1}}^{10} {\sum\nolimits_{{i_{22} = 1}}^{10} {\sum\nolimits_{{i_{13} = 1}}^{10} {\sum\nolimits_{{i_{23} = 1}}^{10} {D_{2} \lambda s_{6} } } } } } } }}{{\pi \sum\nolimits_{{i_{11} = 1}}^{10} {\sum\nolimits_{{i_{21} = 1}}^{10} {\sum\nolimits_{{i_{12} = 1}}^{10} {\sum\nolimits_{{i_{22} = 1}}^{10} {\sum\nolimits_{{i_{13} = 1}}^{10} {\sum\nolimits_{{i_{23} = 1}}^{10} {D_{2} s_{5} } } } } } } }},$$

(49)

$$C = \frac{{\sum\nolimits_{{i_{11} = 1}}^{10} {\sum\nolimits_{{i_{21} = 1}}^{10} {\sum\nolimits_{{i_{12} = 1}}^{10} {\sum\nolimits_{{i_{22} = 1}}^{10} {\sum\nolimits_{{i_{13} = 1}}^{10} {\sum\nolimits_{{i_{23} = 1}}^{10} {D_{2} \lambda^{2} \left( {4s_{5} s_{7} - s_{6}^{2} } \right)} } } } } } }}{{2\pi^{2} \sum\nolimits_{{i_{11} = 1}}^{10} {\sum\nolimits_{{i_{21} = 1}}^{10} {\sum\nolimits_{{i_{12} = 1}}^{10} {\sum\nolimits_{{i_{22} = 1}}^{10} {\sum\nolimits_{{i_{13} = 1}}^{10} {\sum\nolimits_{{i_{23} = 1}}^{10} {D_{2} s_{5} } } } } } } }},$$

(50)

$$F = 8\left( {0.545C_{n}^{2} } \right)^{\frac{6}{5}} k^{\frac{2}{5}} ,\quad D_{2} = \frac{{F_{{i_{11} }} F_{{_{{i_{21} }} }}^{ * } F_{{i_{12} }} F_{{i_{22} }}^{ * } F_{{i_{13} }} F_{{i_{23} }}^{ * } }}{{p_{3} p_{4} p_{5} p_{6} }}\sqrt {\frac{\pi }{{s_{5} }}} ,$$

(51)

$$s_{5} = \frac{{4G_{{i_{13} }} }}{{h_{1}^{2} }} + \frac{{4G_{{i_{23} }}^{ * } }}{{h_{1}^{2} }} - \frac{{u_{3}^{2} }}{{4p_{6}^{2} }} + \frac{{\pi^{2} }}{{b_{3}^{2} p_{5}^{2} \lambda^{2} }} + \frac{{\pi^{2} }}{{b_{3}^{2} p_{6}^{2} \lambda^{2} }} + \frac{{i\pi u_{3} }}{{b_{3} p_{6}^{2} \lambda }},$$

(52)

$$s_{6} = \frac{{4G_{{i_{13} }} }}{{h_{1}^{2} }} - \frac{{4G_{{i_{23} }}^{ * } }}{{h_{1}^{2} }} - \frac{{u_{3}^{2} }}{{4p_{6}^{2} }} + \frac{{\pi^{2} }}{{b_{3}^{2} p_{5}^{2} \lambda^{2} }} - \frac{{\pi^{2} }}{{b_{3}^{2} p_{6}^{2} \lambda^{2} }} + \frac{{2id_{3} \pi }}{{b_{3} \lambda }},$$

(53)

$$s_{7} = \frac{{4G_{{i_{13} }} }}{{h_{1}^{2} }} + \frac{{4G_{{i_{23} }}^{ * } }}{{h_{1}^{2} }} - \frac{{u_{3}^{2} }}{{4p_{6}^{2} }} + \frac{{\pi^{2} }}{{b_{3}^{2} p_{5}^{2} \lambda^{2} }} + \frac{{\pi^{2} }}{{b_{3}^{2} p_{6}^{2} \lambda^{2} }} - \frac{{i\pi u_{3} }}{{b_{3} p_{6}^{2} \lambda }}.$$

(54)

From Eq. (48), we obtain the far-field divergence angle, which is given by

$$\theta = \mathop {\lim }\limits_{L \to \infty } {{w(L)} \mathord{\left/ {\vphantom {{w(L)} L}} \right. \kern-0pt} L} = \sqrt {C + FL^{{{6 \mathord{\left/ {\vphantom {6 5}} \right. \kern-0pt} 5}}} } .$$

(55)

The first three terms on the right-hand side in Eq. (48) represent the mean-squared beam width in free space, and the first term on the right-hand side in Eq. (55) denotes the far-field divergence angle in free space. On the other hand, the last terms in Eqs. (48) and (55) describe effects of turbulence on the mean-squared beam width and the far-field divergence angle, respectively, which are independent of the beam parameters.

The mean-squared beam width w and the far-field divergence angle θ versus δ are shown in Figs. 9 and 10, respectively. It can be seen that w reaches its minimum near the position δ = 0, e.g., δ = 39 μm > 0 in Fig. 9, which is independent of α and $C_{n}^{2}$. However, θ reaches its minimum when δ = 0, which is also independent of α and $C_{n}^{2}$. In addition, from Figs. 9 and 10, we can see that the influence of α on w and θ can be neglected nearly. Furthermore, the influence of turbulence on w and θ can be observed only near their minimum positions.

Fig. 9

Changes of the mean-squared beam width w versus the defocus parameter δ. w ₀ = 1 mm, λ = 1.06 μm, Δx = D = 0, h ₁ = 100 mm, h ₂ = 20 mm, f = 500 mm, L = 5 km

Fig. 10

Changes of the far-field divergence angle θ versus the defocus parameter δ. w ₀ = 1 mm, λ = 1.06 μm, Δx = D = 0, h ₁ = 100 mm, h ₂ = 20 mm, f = 500 mm, L = 25 km

4 Conclusions

In this paper, characteristics of tilted and off-axis partially coherent beams reflected back by a cat-eye optical lens in atmospheric turbulence have been studied in detail. Taking the GSM beam as a typical example of partially coherent beams, analytical expressions for the centroid position deviation γ, the average intensity, the mean-squared beam width w and the far-field divergence angle θ at the receiver plane have been derived.

For unapertured case, γ is independent of beam coherence and atmospheric turbulence, and active detection laser beams can be reflected back by a cat-eye optical lens in the direction of the source exactly if Df = Δx or Lδ = f(f + δ) is satisfied. However, for the apertured case, active detection laser beams can be reflected back by a cat-eye optical lens in the direction of the source exactly only when D = Δx = 0 is satisfied (i.e., perpendicular incidence). The absolute deviation $\left| \gamma \right|$ decreases greatly due to aperture effect. $\left| \gamma \right|$ increases as the beam coherence parameter α increases. Furthermore, $\left| \gamma \right|$ decreases when the turbulence is not strong enough, while $\left| \gamma \right|$ increases when the turbulence is strong enough.

For the perpendicular incidence case, the average intensity, the mean-squared beam width w and the far-field divergence angle θ at the receiver plane have also been examined. In absence of turbulence, the on-axis average intensity may reach a maximum if a suitable small positive defocus parameter δ is chosen, but this advantage is not evident in turbulence. The θ reaches a minimum for the focus case (i.e., δ = 0). The influence of the beam coherence on w and θ can be neglected nearly. Furthermore, the influence of turbulence on w and θ can be observed only near their minimum positions.

The results obtained in this paper are very useful for applications of the active laser detection. Active laser detection based on the cat-eye effect is a new type of technique used in laser weapons. Because the cat-eye optical lens is a non-cooperative target in applications, the active detection laser beam is usually tilted and off-axis, as a result of which the laser beam cannot be reflected back by the cat-eye optical lens in the direction of the source. The absolute deviation $\left| \gamma \right|$ increases as $\left| D \right|$ and $\left| {\Updelta x} \right|$ increase. It is clear that the target will not be detected when $\left| \gamma \right|$ is larger than a certain value. In this paper, we find out that the $\left| \gamma \right|$ decreases as the beam coherence parameter α decreases. Therefore, partially coherent beams are more suitable as active detection laser beams than fully coherent ones.