1 Introduction

Many precision experiments in modern atomic laser spectroscopy and quantum optics are carried out in an externally applied DC magnetic field, produced by a combination of Helmholtz coils and/or solenoids. The precise knowledge of the amplitude and orientation of the magnetic field is a paramount importance for accurate measurements.

In principle, magnetic field distributions can be calculated from the known distributions of coil currents. Alternatively, the spatial field distribution can be mapped by scanning an appropriate magnetometer, such as a fluxgate magnetometer, through the volume of interest. However, there are several technological issues related to those approaches. First of all, many experiments are carried out inside of a passive magnetic shield that will distort the field produced by the coils, an effect which is difficult to account for by quantitative modeling. Secondly, there may be experimental imprecisions associated with the correct placement of the atomic sample (often a vapor contained in a glass cell) with respect to the mapped volume. Moreover, depending on the sample used, the signals from the specific laser spectroscopy experiment may depend on the volume-averaged magnetic field (such as in cells with wall coatings) or on the field averaged over the laser–atom interaction volume (such as in high buffer gas experiments). Other types of experiments (such as in atomic beams or in atom traps) may render it difficult to insert magnetometers at the positions of interest.

The most elegant way around these complications is a field calibration method that uses the atomic sample itself, and in fact such methods have been deployed in the past [1, 2]. Using the atomic sample proper for the calibration has furthermore the distinct advantage that the aforementioned volume averages are intrinsically taken into account. The precise knowledge of all three-vector components of the field applied to the sample implies two distinct aspects. On one hand, the coils have to be calibrated, and on the other hand, one has to determine the residual field components, i.e., the magnetic field present in the sample, when the coils are not powered. One expects the calibration constant to be rather stable over time, unless temperature changes, e.g., affect the coil geometry. In that sense, calibration procedures do not have to be executed at short time intervals. The residual field, however, may change on a daily basis, because of magnetized material being moved in the vicinity of the experiment, or because of uncontrollable changes of the properties of a magnetic shield.

In this paper, we will present efficient methods, both for calibrating the coils and for determining (and compensating) the residual fields. The calibration constants are inferred from the recording and analysis of free-induction decay signals [3] following an optical pumping pulse with resonant linearly polarized light, while we use the ground state Hanle effect to null the residual fields.

We present a proof-of-concept study using the free-induction decay of atomic alignment in a paraffin-coated cesium vapor cell for calibrating a solenoid and two rectangular coil pairs. However, the method can be generally applied to any coil system using any atomic medium, in which spin polarization (orientation or alignment) can be created and detected by the interaction with a resonant laser beam.

2 Coil calibration

2.1 Calibration constants

We assume the laser beam to propagate along the direction \(\hat{k}\) in the horizontal plane, and assume furthermore that the experimental setup is equipped with three independent coil systems generating fields along \(\hat{k}\) and along two orthogonal directions. We will refer to the three magnetic field components as B k, B v, and B h, denoting, respectively, the components along \(\hat{k}\) and along the vertical \((\hat{{\rm v}})\) and horizontal \(({\hat{{\rm h}}})\) directions perpendicular to \({\hat{k}}\). In the calibration procedure reported below, we apply mutually orthogonal magnetic fields B produced by three distinct coil systems and determine for each field configuration the atomic Larmor frequency ω L = 2π ν L = γ F |B|, where γ F is the gyromagnetic ratio of the ground state hyperfine level F on which the experiments are performed. The linear relationship between |B| and ν L is assured as long as the field is small enough, so that contributions from the quadratic Zeeman effect can be neglected.

Figure 1 shows for each coil the drive scheme used in our setup: a control voltage generates a constant current by a voltage-controlled current source that drives the coil(s). The control voltage has two independent input: V inull for nulling the residual field and V i that produces the current I i generating the field components B i .

Fig. 1
figure 1

A control voltage produces a constant current using a voltage-controlled current source (V/I) driving the coil(s). V inull is used to nulling the residual field, while V i controls the current I i generating the field component B i which induces Larmor precession at frequency ν i or 2ν i . The calibration constant η i connects the Larmor frequency to the control voltage via ν i  = η i V i

Full size image

The calibration constants η i , with i = k, h, v, relate the corresponding Larmor frequencies ν i to the control voltages V i , according to ν i  = η i V i .

2.2 Free-induction decay of atomic alignment

The calibration procedure consists in inferring the atomic Larmor frequency from the free-induction decay (FID) of atomic alignment in a time-resolved pump–probe experiment. A high-intensity pulse of resonant linearly polarized laser light produces atomic alignment along the laser polarization direction (pump process). After allowing spin polarization to build up, the (pump) laser power is stepped down to a lower (probe) level. The alignment produced by the pump pulse precesses in the magnetic field to be calibrated while relaxing exponentially (free-induction decay, FID). The decaying precession is probed by monitoring the time-dependent power of the probe beam transmitted by the atomic medium. The probe power is chosen such that it does not significantly influence the polarization during its evolution in the field. We note that recently similar FID signals have been used in a vapor-cell-atomic magnetometer monitoring the earth’s magnetic field [4], and in a cold-atom magnetometer for real-time vector component measurements [5].

2.3 Model

As discussed in [2], the laser power transmitted through an (optically thin) atomic medium is given by

$$ P(t)=P_0-P_0 \kappa_0L+P_0 \alpha \kappa_0L m_{2,0}(t) , $$
(1)

where κ 0 is the peak optical absorption coefficient, L the column length of the vapor, and \(\alpha\equiv\alpha_{F,F^{\prime}}\) the specific alignment analyzing power of the \(F\rightarrow F^{\prime}\) hyperfine transition introduced in [2]. The numerical values of the constants κ 0, L, and \(\alpha_{F,F^{\prime}}\) are irrelevant for the procedure outlined below.

Optical pumping with linearly polarized light creates a tensor spin polarization (alignment) in the medium that is described by the longitudinal atomic multipole moment [6] m 2,0 in a reference frame with quantization axis along the light polarization \(\hat{\varepsilon}.\) Under the torque exerted by the magnetic field, the alignment undergoes a free-induction decay m 2,0(t), which manifest itself as a damped oscillation of the transmitted power by virtue of (1).

The dynamic evolution of the initial alignment m 2,0(t = 0) prepared by the pump pulse is governed by a set of five linear differential equations, given, e.g., in [2]. Under the assumption that the longitudinal \((\varGamma_0)\) and two transverses (\(\varGamma_1\) and \(\varGamma_2\)) relaxation rates are equal to \(\varGamma\), the time dependence of the relevant longitudinal alignment m 2,0(t) is given by

$$ \frac{m_{2,0}(t)}{m_{2,0}(0)}=\left[ \left(\frac{\omega_\perp^2-2\omega_\parallel^2}{2\omega_{\rm L}^2}\right)^2 + 3 \frac{\omega_\parallel^2 \omega_\perp^2}{\omega_{\rm L}^4}\cos(\omega_{\rm L} t) +\frac{3\omega_\perp^4}{4\omega_{\rm L}^4}\cos(2\omega_{\rm L} t) \right] e^{- \varGamma t} . $$
(2)

The Larmor frequencies ω ∥ and ω⊥ are associated with the magnetic field components B ∥ and B ⊥ that are, respectively, parallel and perpendicular to the light polarization \(\hat{\varepsilon}.\) They obey \(\sqrt{\omega_\parallel^2 + \omega_\perp^2}=\omega_{\rm L}=\gamma_F |{\bf B}|.\)

It has been shown before [2, 8] that the orientational dependence of alignment-based magnetometers depends on a single geometrical parameter θ, viz., the angle between the light polarization \(\hat{\varepsilon}\) and the magnetic field. The above result (2) can therefore also be expressed as

$$ \begin{aligned} \frac{m_{2,0}(t)}{m_{2,0}(0)} &=\left[ \left(\frac{3\cos^2\theta-1}{2}\right)^2 \right.\\ &\quad\left.+\,3\cos^2\theta\sin^2\theta\cos(\omega_{\rm L} t)\,+\,\frac{3}{4} \sin^4\theta\cos(2\omega_{\rm L} t)\right]e^{- \varGamma t} \end{aligned} $$
(3)
$$\quad =\sum_{q=-2}^{q=+2} |C_{2,q}(\theta,0)|^2 \cos(q\omega_{\rm L} t)e^{- \varGamma t} , $$
(4)

where \(C_{2,q}(\theta,\varphi)=\sqrt{4\pi/5} Y_{2,q}(\theta,\varphi).\) It is interesting to note the similarity of (4) derived here and Eq. (14) of [2] describing the ground state Hanle effect with linearly polarized light. This is not surprising since the experimental method described here is the time domain equivalent of the experiments reported in [2], so that Eq. (14) of [2] is the ω = 0 component of the Fourier transform of m 2,0(t) derived here.

One sees that a pure longitudinal magnetic field (θ = 0, equivalent ω ⊥ = 0) does not produce any time-dependent (FID) signal. All calibration experiments are thus carried out in pure transverse fields (θ = π/2), for which the time dependence of the alignment reduces to

$$ m_{2,0}(t)= \frac{m_{2,0}(0)}{4}\left[1+3 \cos(2 \omega_{\rm L} t) \right] e^{-\varGamma t} , $$
(5)

which, after insertion into (1), yields for the power after the cell

$$ P(t)=A_1+A_2 e^{-\varGamma t}+3A_2 \cos(2 \omega_{\rm L} t) e^{-\varGamma t} , $$
(6)

with

$$ A_1=P_0(1-\kappa_0L) $$
(7)
$$ A_2=\frac{1}{4} P_0 \alpha \kappa_0L m_{2,0}(0) $$
(8)

The FID signal (6) represents an oscillation at twice the Larmor frequency with initial amplitude 3A 2 superposed on a background signal of amplitude A 2, both decaying exponentially at rate \(\varGamma\) toward the asymptotic power level \(P(t\gg\varGamma^{-1})=A.\) The contrast of the FID signal (i.e., the ratio of the oscillatory and the asymptotic values of the photocurrent at t = 0) is given by

$$ \frac{4A_2}{A_1}\approx m_{2,0}(0) \alpha \kappa_0L , $$
(9)

to first order in κ 0 L.

We note that, according to (2), the contamination of a nominally pure transverse field ω ⊥ by a small longitudinal field component ω ∥ ≪  ω ⊥ leads to the appearance of a Fourier component at ω L, whose amplitude relative to the dominating 2 ω L component is (2 ω ∥/ω ⊥)2.

3 Experiments

3.1 Apparatus

We carried out the experiments reported below in a spherical (30 mm diameter) paraffin-coated Cs vapor cell [7] at room temperature using a linearly polarized diode laser beam. The laser frequency was actively stabilized to the \(F_g=4 \rightarrow F_e=3\) hyperfine component of the \(D_1\;(6^2S_{1/2}\;\rightarrow\;6^2P_{1/2})\) transition. The power of the transmitted light was detected by a biased photodiode followed by a current-voltage converter, and the FID signals were stored on a digital oscilloscope. We used a (600 mm long, 209 mm diameter) solenoid for the B k field and two pairs of (600 mm long, 184 mm wide) rectangular coils in Helmholtz configuration for the B h and B v fields, respectively. The cell and coils were mounted inside of a two-layer mu-metal shield (inner diameter = 550 mm, length = 1,200 mm) without end caps. The current through the rectangular coils was controlled by two independent (nominally identical) home-made voltage-controlled current sources, producing up to \(\pm20\;\hbox{mA}\;(\pm9\;\upmu\hbox{T})\) with a precision of 2 nA. The current source for the solenoid produces up to \(\pm4\;\hbox{mA}\;(\pm6\;\upmu\hbox{T})\) with a precision of 0.4 nA.

3.2 FID recording

Prior to recording the FID signals proper, we have carefully compensated the residual field components to a level of 1 nT using the method outlined in Sect. 5.

Free-induction decay signals were recorded in the following way. First, the atomic vapor is excited by a 1.5 ms long light pulse of typically \(P_{\rm pump}=200\;\upmu\hbox{W},\) after which the light power is reduced to a level of typically \(P_{\rm probe}=4\;\upmu\hbox{W}\) for \(\approx\)150 ms. The laser power control is achieved by a combination of an electro-optic modulator and a linear polarizer. The pump pulse prepares the atomic alignment, whose free evolution and relaxation is then detected by monitoring the time dependence of the transmitted probe beam’s power, yielding a signal S FID(t) proportional to (6). The signal S FID(t) is recorded on a digital 8-bit storage oscilloscope by averaging 512 time traces of ≈150 ms duration.

In this way, we calibrate the three coil systems sequentially, by recording the FID signals for a set of control voltage values \(V_{\rm k},\;V_{\rm h}\) and V v, respectively, using the geometries shown in Fig. 2.

Fig. 2
figure 2

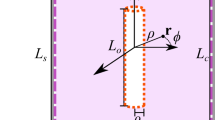
Geometries used to calibrate the coils producing the fields B k (a), B h (b), and B v (c), respectively. \(\hat{\varepsilon}\) represents the light polarization used for the three calibrations. The laser beam propagates along \(\hat{k}.\) The same beam serves to pump and probe the atoms. During the probe process, the laser intensity is lowered. PD indicates the photodetector

Full size image

In all three geometries, the light polarization \(\hat{\varepsilon}\) is orthogonal to the direction of the field to be calibrated (θ = π/2), so that the FID signal is expected to contain no oscillation at the fundamental of the Larmor frequency ω L.

4 Data analysis and results

The upper trace of Fig. 3 shows typical raw data S FID(t) of an FID signal recorded during calibration the field B k. In the off-line analysis, we first apply a digital high-pass filter to the data (details given in “Appendix”) to suppress the constant and exponentially decaying background given by the first two terms of (6). The central trace of Fig. 3 shows the high-pass filtered data, together with a fit of the form \(S_{\rm FID}^{\rm hpf}(t)=3B \cos{(2\pi 2\nu_{\rm L} t)},\) yielding 2νL=1,766.45(2) Hz. The decay time of the FID signal is \(\varGamma^{-1}=35.04(3)\;\hbox{ms}.\)

Fig. 3
figure 3

FID data recorded in the geometry of Fig. 2a with a control voltage V k = 0.390 V. Upper trace raw data S FID(t) with overlaid background from bottom figure. Middle trace high-pass filtered FID data S hpfFID (t) (dots) together with FID fit. Lower trace difference of raw data from upper trace and fitted function from middle trace, together with a fitted function (exponential decay plus constant amplitude sine wave). These background data, together with their fit, are overlaid in the top figure

Full size image

The lower trace \(\varDelta S\) represents the difference in the raw data (upper trace) and the fitted function of the middle trace of Fig. 3. These background data show a signal decaying with a time constant of 116(8) ms and a superposed oscillation at 250 Hz, due to a photocurrent pickup contamination of unknown origin, as expected from the first two terms of (6). These background data show a signal decaying with a time constant of 116(8) ms, as expected from the first two terms of (6), and a superposed oscillation at 250 Hz, due to a photocurrent pickup contamination of unknown origin.

The fact that the decay constants of the FID proper and of the background differ is probably due to the fact that the longitudinal and transverse relaxation rates are different. The bottom trace illustrates well that there is no contribution at ω L in the data, as expected from the chosen geometry \((\hat{\varepsilon}\perp\hat{B}_{\rm k}).\)

The fit quality is also evidenced in Fig. 4, where we show the filtered FID signals, together with fitted curves and fit residuals for two selected field values.

Fig. 4
figure 4

Filtered FID data recorded in the geometry of Fig. 2a, together with fits and residuals for B k ≈ 267 nT (top traces) and B k ≈ 524 nT (bottom traces)

Full size image

4.1 Calibration results

Figure 5 shows a typical example of calibration data for the solenoid (B k-field). The FID oscillation frequencies were measured both for positive and negative V k values, and the results are symmetric as expected.

Fig. 5
figure 5

Calibration of the solenoid field B k from dependence of FID oscillation frequencies 2νL on the control voltage V k. Top measurements with pump/probe power levels of 18/2 μW (blue circles), and of 200/4 μW (red squares). Bottom fit residuals

Full size image

Data were taken with two different combinations of pump/probe power (see caption of Fig. 5) and the data were fitted by linear dependencies on V k, i.e., B k = η k V k + B res.k ., allowing for a residual field B res.k whose value compatible with zero. The fitted residual field value is compatible with zero and the calibration constants were found to be \(\eta_{\rm k}=2.264(7)\;\hbox{Hz/mV}\) for the 18/2 μW data and \(\eta_{\rm k}=2.260(5)\;\hbox{Hz/mV}\) for the 200/4 μW data. From the consistency of the two values, we conclude that the FID frequency does not critically depend on the pump and probe power. The average of the two calibrations yields \(\eta_{\rm k}=2.262(4)\;\hbox{Hz/mV}\) corresponding to a relative precision δη k/η k = 2 × 10−3.

4.2 Discussion

We note that the typical statistical uncertainty in the Larmor frequency determination from a single (time averaged) FID trace is on the order of 10 mHz, corresponding to δν L/νL on the order of 10−5. This precision is compatible with the expectation for a Cramér-Rao (CR) limited frequency determination [9] of a damped sine wave with a signal/noise ratio that is 20 dB above shot noise.

The fact that the achieved precision is two orders of magnitude worse than the precision of the individual frequency determinations can be traced back to the ‰ precision of the individual measurements of the control voltages V i performed by the oscilloscope.

We have applied the same procedure for calibrating the B h and B v coils and obtained calibration constants with a similar precision. At an earlier stage, we have calibrated the same coils using the ODMR method with circularly polarized light discussed in [1, 2]. The calibration constants from those measurements are compatible with the present determination and have comparable uncertainties.

5 Residual magnetic field

As stated in the introduction, the precision control of the magnetic field involves, besides coil calibration, the precise compensation of the residual magnetic field components that are present when the coils are not powered. Currently, we determine the residual field vector using the ground state Hanle effect with linearly polarized light (LGSHE). LGSHE resonances are recorded by monitoring the transmitted laser power while scanning a selected field component B s through B s  = 0.

In [2], we have derived algebraic expressions for the lineshapes observed in LGSHE spectroscopy. Here, we make use of the fact that no resonance is observed when the scanned field is perfectly parallel to the light polarization \(\hat{\varepsilon},\) i.e., when there are no spurious field components in the directions perpendicular to \(\hat{B}_s.\) This is illustrated in Fig. 6, where scan the component B h parallel to the light polarization \(\hat{\varepsilon}=\hat{h}.\) The central plot of the figure shows the absence of the Hanle resonance, when the components B k and B v are perfectly nulled, while the left and right plots of Fig. 6 show the appearance of a Hanle resonance in the presence of small field components along \(\hat{B}_{\rm k}\) and \(\hat{B}_{\rm v},\) respectively. Using the disappearance of the Hanle peak as a criterion, one can null the spurious field components in this way with a precision of ≈1 nT. The residual component of the scanned field (here \(\hat{B}_s=\hat{B}_{\rm h}\)) can be determined from the offset position of the Hanle resonance with respect to B h = 0.

Fig. 6
figure 6

Ground state Hanle effect with linearly polarized light as an efficient method for measuring (and zeroing) residual magnetic field components

Full size image

We note again that the calibration constants are expected to be rather stable over time, but that varying laboratory fields require the residual fields to be checked at regular time intervals. The Hanle resonance method has proven to be a fast and efficient method for achieving this.

An alternative—not yet evaluated—method for nulling the residual field components could use the FID signals proper. Since most modern digital oscilloscopes have a built-in fast Fourier transform (FFT) capability, one might monitor the Fourier spectrum over a frequency range scanning ν L and 2ν L while shining a periodic sequence of the pump–probe pulses. By iteratively adjusting all three field control voltages such that the peaks at both ν L and 2ν L vanish, one could achieve perfect field-free conditions. The sensitivity of this method is currently under evaluation.

6 Summary and conclusion

We have presented a simple method for calibrating a three-axis coil system based on the free-induction decay of atomic alignment prepared by optical pumping with resonant linearly polarized laser light. We have demonstrated that the fitting of high-pass filtered FID data can—in principle—provide 10 ppm precision in the FID frequency determination. In the proof-of-concept measurements reported here, the precision of the calibration constants was limited to the ‰ level because of the 8-bit resolution of the oscilloscope.

We have previously used optically detected magnetic resonance (ODMR) spectroscopy for field calibration, which, because of the same limiting factors, has yielded a similar ‰ precision. Compared to the ODMR method, the FID method presented here offers three main advantages: (1) the experimental apparatus is simpler: no rf magnetic field and no lock-in detection is needed; (2) the calibrations of all three coils are independent, and (3) the calibration curves all depend in a linear manner on the field control voltage.

We finally point out that the presented calibration in frequency units circumvents the requirement to know the magnetic field on an absolute scale, which is of practical use when measuring, e.g., frequency shifts or relaxation times.