Precise control of the properties of light propagation along linear waveguides has always been of great importance in the world of optics and same as terahertz field. Surface plasmon polaritons (SPPs) provide the possibility of localizing and guiding electromagnetic (EM) waves in subwavelength metallic structures and constructing miniaturized optoelectronic circuits [1, 2]. The plasmonic structure could confine the EM energy within subwavelength dimensions over a wide spectral range [3–6]. And different surface structures or material interfaces can cause significant changes in the properties of the transmitted or propagated EM fields [7, 8], which is especially important for slowing light. Slow light is a key technology in areas of optical modulators, optical sensors, and nonlinear enhancement [9–13]. Based on this feature, it is already demonstrated that a kind of graded depth grating structure could confine, focus, slowdown, and even stop the THz waves along the metal surface [14, 15]. However, no one gives how much the exact propagation speed of the THz waves is, and how to realize a specific slow propagation speed. These problems are discussed in this letter and demonstrated using a two-dimensional (2D) finite-difference time-domain (FDTD) simulation technique.

It is known that, at THz frequencies, metals resemble in many ways a perfect conductor, and the negligible penetration of the EM fields leads to highly delocalized SPPs. However, periodically structured metal surface with grooves can achieve subwavelength confinement in metal gratings at THz or microwave frequencies [14, 15], because the dispersion relation of SPPs can be engineered at will by designing the parameters of surface grating. In this way, the confinement does not rely on the finite conductivity of the metal but is purely due to the surface structure. With such a structure, plasmonics could enable THz waves applied in many promising fields, such as near-field imaging [16] or biosensing [17], with unprecedented sensitivity. Basically, such a one-dimensional (1D) grating engraved in the metal surface has three-dimensional parameters: depth (d), width (w), and period (p).

The metallic structures based on SPPs in THz and GHz domains, as an approximation to the metals, could be treated as perfect electrical conductors (PEC). Then, the dispersion relation for TM-polarized (Ex, Ez, Hy) EM waves propagating in the x direction along the surface grating structure can be expressed as below:

$$ k = \frac{\omega }{c}\sqrt {1 + \frac{{w^{2} }}{{p^{2} }}{ \tan }^{2} \left( {\frac{\omega }{c}d} \right)} $$
(1)

where c is the light velocity in vacuum. This is a first-order approximation. It is just an approximate expression to simplify and illustrate the principle of grating design. In fact, the cutoff frequency estimated from Eq. (1) will be slightly larger than FDTD simulation. In order to attain a more precise prediction, an eigenvalue equation in the corrugated conducting plane of a periodic system need to be introduced, and higher-order scattering components should be taken into account [18].

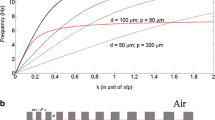
The dispersion relations for the 1D groove grating with different depths can be obtained by solving Eq. (1), which is shown in Fig. 1a. The blue line (d = 60 μm) and red line (d = 120 μm) in Fig. 1a show different dispersion property while changing the groove depth (d). Figure 1b shows the schematic of the graded depth (grating 1) and partial graded depth (grating 2) metal grating structure.

Fig. 1
figure 1

a Dispersion curves calculated for different grating depth (d): d = 60 μm (blue line), d = 120 μm (red line), light in vacuum (green dotted line), b schematic of a graded depth metal grating 1 and partial graded depth metal grating 2, with width (w), period (p), and depth (d)

Full size image

For d = 60 μm, the cutoff frequency of the dispersion curve is close to 1.1 THz, which means the corresponding structure is capable of supporting the surface EM modes in the grating structure at such a frequency, as demonstrated below by using FDTD simulations. For d = 120 μm, the cutoff frequency of the grating structure is reduced to about 0.6 THz. Therefore, the EM wave at 0.6 THz could be coupled, confined, and propagated along the grating structure. With the depth increasing, the cutoff frequency of the dispersion curve is decreased. The period (p) and width (w) are set as 50 and 25 μm, respectively.

As illustrated by the dispersion relations in Fig. 1a, the normal surface grating structures are capable of slowdown, confine, and propagate the EM waves. In this case, the surface grating structures with 1D periodic subwavelength grooves can work as a waveguide for slow EM modes propagation at various frequencies with specific designed surface gratings [19, 20]. However, it is almost impossible to use a single-depth grating as ultraslow waveguide. Because the supported ultraslow frequency must be close to the corresponding cutoff frequency, the wave vector mismatch (Δk) between the dispersion curve and light line (green dotted line) is too large (Fig. 1a). If the depth of the grating is graded linearly along the whole grating, the dispersion curves of the graded depths grating will differ from those for a constant grating depth. For a grating with graded depth changing from 60 to 120 μm, the dispersion curves will be located between the blue line and red line, as shown in Fig. 1a. Therefore, the cutoff frequency of the graded structure decreased from 1.1 to 0.6 THz, which means a broadband EM waves within a frequency band of 0.6–1.1 THz can be slowed down in such a single-graded depth grating structure, even completely stopped at the different locations along the surface grating. The propagation group velocity (v g) can be deduced from Eq. (1):

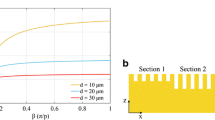
$$ v_{g} = \frac{{{\text{d}}\omega }}{{{\text{d}}k}} = \frac{c}{{G + \frac{{w^{2} d}}{{Gcp^{2} }}\omega \tan \left( {\frac{\omega }{c}d} \right){ \sec }^{2} \left( {\frac{\omega }{c}d} \right)}} $$
(2)

where \( {\text{G}} = \sqrt {1 + \frac{{w^{2} }}{{p^{2} }}{ \tan }^{2} (\frac{\omega }{c}d)} \). It can be seen from Fig. 2, when the depth close to zero, the group velocity equals to the light velocity in vacuum. As the grating depth increases, the group velocity will slow down (Fig. 2). It drops to zero at certain depth point and even goes to be negative after that point which is different for different frequencies. Figure 2 also shows that higher frequencies slow down faster and stop first at a smaller depth, i.e., frequency of 1.1 THz will stop at a depth of 70 μm and frequency of 0.6 THz will stop at depth of 120 μm. The graded depth grating structure (grating 1 shown in Fig. 1b) can definitely work as a wave trapper. Except for that, it can also work as an ultraslow waveguide for different frequencies by just fixing the grating depth when the depth increases to a certain value (grating 2 shown in Fig. 1b). For example, if the grating depth linearly changes to 85 μm and fixes from this point, the frequency of 0.9 THz (green line in Fig. 2) will be stopped, but the frequency of 0.8 THz (black line in Fig. 2) will be still propagated in a very small group velocity which is around 107 m/s (1/30 of light speed in vacuum), which could be reduced further to close zero by using a grating depth of 95 μm.

Fig. 2
figure 2

Calculated group velocities (v g) of different grating depths (d) at different frequencies: red line (0.6 THz); blue line (0.7 THz); black line (0.8 THz); green line (0.9 THz); cyan line (1.0 THz); magenta line (1.1 THz)

Full size image

Figure 3 shows the 2D FDTD simulation results of grating 1 (Fig. 3a–c) and grating 2 (Fig. 3d–f). The 2D EM field distribution of grating 1 shown in Fig. 3a–c shows that three different frequencies are localized and trapped at three various positions corresponding to different grating depth. The EM wave at 0.6 THz is stopped at the location having the depth of approximately 110 μm (Fig. 3a), whereas at 0.75 THz, it is localized at the grating depth of approximately 90 μm (Fig. 3b) and at 0.8 THz is localized at the grating depth of approximately 85 μm. They are a little different from the expected results of Eqs. (1) and (2). That is because Eq. (1) is a first-order approximation, and the cutoff frequency estimated from Eq. (1) is slightly larger than FDTD simulation as mentioned before. The 2D EM field distribution of grating 2 at frequencies of 0.6, 0.75, and 0.8 THz is shown in Fig. 3d–f, respectively. The grating depth is fixed at 85 μm after a distance of graded change. This depth can reduce the speed of 0.8 THz to zero, but still can support lower frequencies propagation. Hence, frequency of 0.8 THz is stopped (Fig. 3f) which is same as that shown in Fig. 3c. However, frequencies of 0.6 and 0.75 THz are all propagated. And the propagation speed of 0.75 THz must be much slower than 0.6 THz, which will be demonstrated later.

Fig. 3
figure 3

Results of 2D FDTD simulations: 2D EM field distribution of grating 1 at three different frequencies of 0.6 THz (a), 0.75 THz (b), and 0.8 THz (c); 2D EM field distribution of grating 2 at the same three different frequencies (d–f)

Full size image

These results are based on a 2D FDTD model (Fig. 1b) simulation and clearly confirm that different frequencies stop at different positions along the grating 1, and some of the frequencies can propagate along grating 2 working as an ultraslow waveguide. We can surely tune the working frequency range of the grating structure by using another different grating depth. The dispersed pulse of such a structure has a very steady state distribution, so that the spectrum information could be obtained conveniently. The thickness of the metal is set to be 300 μm. The incident wave is a pulsed source with a centered frequency at 1 THz. The full width at half-maximum (FWHM) of the pulse in frequency domain is around 0.6–1.3 THz, so that the structure response of any frequency in this range can be simulated.

The total length of the grating structure is 5 mm. The propagation time (t p) should be calculated as 5 mm/c, and the simulation time (t s) is set to t s = 100 t p = 500 mm/c. The simulation time is already far beyond the EM waves propagating time in free space. That is to make sure the simulated slowing down effect is reliable. The dimension of the simulated region is 5,000 μm × 800 μm with a uniform cell of Δx = 2 μm and Δz = 2 μm. The simulated region is surrounded by a perfectly matched layer absorber. The FDTD simulation results show that different frequencies are localized at different locations along the grating 1 and propagated along the grating 2 after a long simulation time (t s = 100 t p) and stay unchanged using even much longer calculation time, confirming whether the group velocity of the SPP modes has been reduced to nearly zero (grating 1) or not (grating 2).

It is already demonstrated that the grating 2 can be used to slowdown the EM wave packet on the surface and work as an ultraslow EM wave waveguide. The propagation speed is also depending on the frequencies of the incoming EM waves. Next, the real propagation speed will be calculated according to the propagating length at different time. The 1D EM intensity (|E|2) distributions along the grating 2 are shown in Fig. 4. The wave packet of 0.6 THz is propagated to x = −500 μm after a time t 0 (red line in Fig. 4a) and to x = 1,200 μm after a time t 0 + t 1 (black line in Fig. 4a). The total propagation length in time t 1 is around 1,700 μm. The absolute value of t 1 is about 2.4 × 10−11 s, which is an increased calculation time adding on the calculation time t 0. Then, the propagation speed of 0.6 THz equals 1,700/2.4 × 10−11 = 7.1 × 1013 μm/s, which is about 0.24 times of light speed in vacuum. For the frequency of 0.75 THz shown in Fig. 4b, the propagation speed becomes much slower. The total propagation length in time t 1 is only around 50 μm. Then, the propagation speed of 0.75 THz equals 50/2.4 × 10−11 = 2.1 × 1012 μm/s, which is about 0.007 times of light speed in vacuum. And the real propagation speed can be designed by tuning the grating depth according to the application demand. The micrometer-scale dimensions of the structure for THz waves can be easily realized by current fabrication technologies.

Fig. 4
figure 4

1D EM intensity (|E|2) distribution along the structured metal surface (grating 2) at different frequencies: a 0.6 THz, b 0.75 THz

Full size image

In conclusion, when the grating depth is graded, the dispersion curves of the surface structure are dramatically changed and become spatially inhomogeneous. Such grating structures are capable of slowing down EM waves within an ultrawide spectral band along the surface. We have demonstrated a metal surface structure with combined graded and fixed depth grating can support ultraslow THz SPP modes and calculated the real propagation speed which could be reduced to be nearly zero according to the real application demand, which is almost impossible for a single-depth grating. The working frequency can be easily widen or shifted by tuning the depth of the grating structure. Such a feature could open a door to exactly control the EM waves on a chip or even realize novel applications such as signal processing, data storage, and chemical diagnostic integrated on a chip.