1 Introduction

The hybrid structure consisting of a semiconductor quantum dot (SQD) and a metal nanoparticle (MNP) has attracted significant attention in recent years. There is no direct tunneling in such structure, excitons (discrete quantum-confined electronic states in SQD) and plasmons (dielectric-confined electromagnetic modes in the MNP) strongly coupled due to the long-range Coulomb interaction [1]. This still growing interest is driven to a large extent by novel fabrication techniques with that the functionalities of the hybrid system with the tunable size and shape are further increased for better control of optical properties and energy flows on nanometer length and femtosecond time scales [2]. So far, quantum mechanical approach [3, 4] and semiclassical theory [1, 5–12] have been used to describe the hybrid system, respectively. Experimental investigations have shown an enhanced luminescence [13] and enhancement of fluorescence efficiency [14] of the core–shell SQD coupled to MNP. The composition and structure of the SQD–MNP complexes can be controlled well using self-assembly approach [15], besides, the surface plasmon can assist the modal gain enhancement [16].

Theoretical studies demonstrate that exciton–plasmon interactions allow design of absorption and emission properties [1, 5, 7, 8, 12], control of Förster energy transfer processes [17, 18], creation of optical bistability [10], enhancement of photon fields inside the quantum emitter [19–21] and modulation of the quantum optics properties [11, 22, 23]. Exciton–plasmon in SQD–MNP hybrid structure offers a wide range of opportunities to control light-mater interactions. Therefore, the large optical nonlinearities are expected in the hybrid structure. Recently, linear susceptibility dependence on the interparticle distance and material parameters of the hybrid system has been investigated in detail [24]. The second-harmonic generation (SHG) has been studied in a quantum dot–metallic nanoparticle hybrid system [25]. It has been found that the SHG signals are enhanced by the dipole–dipole interaction, and the SHG signal can be switched on and off by applying a control field.

The attraction of the hybrid system arises of their complementary optical properties. The optical excitation in the SQD is the exciton with a sharp, discrete optical response and plasmonic excitations in the MNP with the strong, local field. The former leads to increase emission yield [19] and capability in light harvesting. The latter enables the concentration of electromagnetic energy and enhances optical fields and nonlinearities. Here, we focus theoretically on the hybrid system to understand how the exciton–plasmon coupling affects the four wave mixing (FWM) response of a SQD by considering the multipole polarization of the MNP. In the framework of the effective mass and the rotating wave approximation, we demonstrate the FWM response of the SQD, which is enhanced remarkably in the presence of the MNP by controlling the geometrical parameters of the hybrid structure and the polarized direction of the electric field. However, it is well known that phenomenological treatments will break down when the nanoparticle is very close to each other, due mainly to the neglect of the nonlocal responses of the MNP. Therefore, we give the results corresponding to the local and nonlocal optical response of the MNP, respectively, for the comparison. By investigating a series of different parameter dependence, we confirm that the nonlocal effect should be considered in the special geometrical parameters under which the FWM response shows stronger. The results provide several degrees of freedom for the design and fabrication of structures, which are completely new opportunities for optimizing the nonlinear responses of the SQD.

2 Model and theory

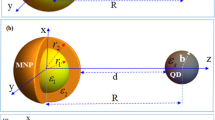
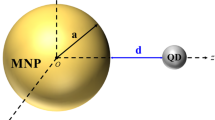
The model we study here consisting of a core–shell CdSe/ZnS SQD with the inner radius(core radius) R 1 and the outer radius R 2 (inner radius plus the shell thickness), and a Au MNP with the radius R m subject to an applied electric field (shown in Fig. 1). The two nanoparticles have a center-to-center distance d and the surface distance d s. We assume that the SQD has a small dimensions i.e., \(R_{2} \ll d\) and the applied field is so large that noise can be ignored. The interaction between exciton and plasmon occurs in the nanometer-scale vicinity of the two material systems, which is revealed as an enhancement or suppression of emission. The former arises the electric field amplified by the plasmon resonance and the latter comes from energy transfer from SQD to MNP. The FWM depends strongly on the geometrical parameters of the system, the physical and material properties of the MNP. We take advantage of the effective mass approximation and local field theory [26] to describe the hybrid system in order to study well the relationship between nonlinear optical response and microscopic parameters. This is a reasonable treatment for our investigation purposes.

Fig. 1
figure 1

The model of hybrid molecule composed of a core–shell CdSe/ZnS quantum dot coupled to an Au nanoparticle

Full size image

The Schrödinger equation for a particle reads

$$\left[ { - \frac{{\hbar^{2} }}{2}\nabla \frac{1}{{m^{ * } }}\nabla + V(r)} \right]\psi (r) = E\psi (r), $$
(1)

in effective mass approximation with single bands for both the conduction and valence-band carriers [27], where \(\hbar\) is Planck’s constant divided by \(2\pi\), \(m^{ * }\) is the effective mass of a carrier. The Coulomb interaction energy of an exciton can be treated as a helium-like perturbation term [28]

$$E_{c} = - \frac{{e^{2} }}{4\pi }\int {\int {{\text{d}}{\mathbf{r}}_{\text{e}} {\text{d}}{\mathbf{r}}_{{\mathbf{h}}} \frac{{\psi_{e}^{ * } ({\mathbf{r}}_{\text{e}} )\psi_{h}^{ * } ({\mathbf{r}}_{h} )\psi_{e} ({\mathbf{r}}_{\text{e}} )\psi_{h} ({\mathbf{r}}_{h} )}}{{\left| {{\mathbf{r}}_{{\mathbf{e}}} - {\mathbf{r}}_{{\mathbf{h}}} } \right|}}} } \cdot \frac{1}{{\varepsilon (r_{e} - r_{h} )}}, $$
(2)

and the new band gap of the core–shell quantum dot material is the sum of the confinement energies, the Coulomb energy and the bulk band gap energy, i.e.,

$$E_{\text{gap}} = E_{e,1s} + E_{h,1s} + E_{c} + E_{{{\text{gap}},{\text{bulk}}}} . $$
(3)

The Eigen solutions of the exciton are obtained numerically, and the continuous and smooth boundary conditions in SQD are added. We consider only the elementary case of two-level system, the optical transition interested in occur between the ground state \(\left| 1 \right\rangle\) and the excited state \(\left| 2 \right\rangle\) of the exciton, with the excite energy \(\hbar \omega_{21}\).

The entire hybrid system subjects to an applied electric field in the form \(E_{0} (t) = \text{Re} (\tilde{E}_{0} e^{ - i\omega t} ) = (\tilde{E}_{0} e^{ - i\omega t} + {\text{c}} . {\text{c}} .)/2.\) The total electric field applied inside the SQD [7] is given by the sum of the three electric vector field

$${{\user2 E}}_{\text{SQD}} = \frac{1}{2}[({{\tilde{\user2 E}}}_{1} + {{\tilde{\user2 E}}}_{2} + {{\tilde{\user2 E}}}_{3} )e^{ - i\omega t} + {\text{c}}.{\text{c}}.], $$
(4)

\({\tilde{\user2 E}}_{1} = \varepsilon_{b} /\varepsilon_{{{\text{eff}}1}} {\tilde{\user2 E}}_{0}\) is the local electric field induced by \(\user2{E}_{0}\) inside a SQD in the absence of a MNP, where \(\varepsilon_{b}\), \(\varepsilon_{s}\) and \(\varepsilon_{{{\text{eff}}1}}\) are the dielectric constants of the background, CdSe quantum dot and the effective permittivity, respectively, and \(\varepsilon_{{{\text{eff}}1}} = (\varepsilon_{s} + 2\varepsilon_{b} )/(3\varepsilon_{b} )\). \(\tilde{E}_{2} = [g_{1} \varepsilon_{b} \gamma_{1} R_{m}^{3} /(\varepsilon_{{{\text{eff}}1}} d^{3} )]\tilde{E}_{0}\) comes from the surface charges of the MNP induced by \(\user2{E}_{0}\) and \({\tilde{\user2 E}}_{3} = \sum\nolimits_{n = 1}^{\infty } {\left[ {{{g_{n} \varepsilon_{b} \gamma_{n} R_{m}^{2n + 1} } \mathord{\left/ {\vphantom {{g_{n} \varepsilon_{b} \gamma_{n} R_{m}^{2n + 1} } {(\varepsilon_{{{\text{eff}}1}} \varepsilon_{{{\text{eff}}2}} d^{2n + 4} )}}} \right. \kern-0pt} {(\varepsilon_{{{\text{eff}}1}} \varepsilon_{{{\text{eff}}2}} d^{2n + 4} )}}} \right]} {{\tilde{\user2 p}}}\) is the effective electric field induced by the dipole (n = 1) and multipole (n > 1) interactions between the SQD and MNP, where \(\varepsilon_{{{\text{eff}}2}} = (\varepsilon_{s} + 2\varepsilon_{b} )/3\), \(\gamma_{1} = [\varepsilon_{m} (\omega ) - \varepsilon_{b} ]/[\varepsilon_{m} (\omega ) + 2\varepsilon_{b} ],\) \(\gamma_{n} = [n(\varepsilon_{m} - \varepsilon_{b} )]/[n(\varepsilon_{m} + \varepsilon_{b} ) + \varepsilon_{b} ],\) \(\varepsilon_{m} (\omega )\) is the dielectric function of the Au, \(g_{1} = 2\;{\text{or}}\;( - 1)\) and \(g_{n} = (n + 1)^{2}\) or \(P_{n}^{\prime } (1)\) for the electric field polarization. \(E_{0}\) is parallel or perpendicular to the major axis of the system, respectively. Here \(P_{n}^{\prime } (1)\) is the derivative of the Legendre function at the argument of 1. In the simplest approximation, we describe the MNP with the local uniform dielectric function \(\varepsilon_{m} (\omega ) = \varepsilon_{m1} (\omega )\) obtained from Ref. [29]. In nonlocal case [30–32], the nonlocal dielectric function \(\varepsilon_{m} (\omega )\) is expressed by \(\varepsilon_{m2} .\) We have the following equation

$$\frac{1}{{\varepsilon_{m2} }} = \left[ {\frac{1}{{\varepsilon_{m1} }} + (2n + 1)\left[ {\frac{{r\omega_{p} }}{\beta u}} \right]^{2} I_{{\frac{2n + 1}{2}}} (u)K_{{\frac{2n + 1}{2}}} (u)} \right], $$
(5)

where \(\beta^{2} = 3v_{\text{F}}^{2} /5\) with the Fermi velocity \(v_{\text{F}} ,\) \(u = R_{m} \sqrt {\omega_{p}^{2} - \omega (\omega + i\gamma )} /\beta ,\) \(I_{\nu } {\kern 1pt}\) and \(K_{\nu }\) are the modified Bessel functions.

The optical nonlinearities of the exciton in the SQD are described in terms of the interband polarization and the occupancy by the optical Bloch equations

$$\dot{\rho }_{22} = \frac{i}{\hbar }{\varvec{\upmu}}_{12} \cdot {\text{E}}(\rho_{21}^{ * } - \rho_{21} ) - \frac{1}{{T_{1} }}\rho_{22} , $$
(6)
$$\dot{\rho }_{21} = - \left( {i\omega_{21} + \frac{1}{{T_{20} }}} \right)\rho_{21} + \frac{i}{\hbar }{\varvec{\upmu}}_{12} \cdot {\mathbf{E}}(\rho_{11} - \rho_{22} ). $$
(7)

The solutions of the Eqs. (6) and (7) can be obtained in the rotating wave and steady state approximation. Substituting them into Eq. (4), the local field factors are given by using the local field effects in nonlinear optics

$$f_{s} = \frac{{\varepsilon_{b} }}{{\varepsilon_{{{\text{eff}}1}} }} $$
(8)
$$f_{2} = f_{s} \left( {1 + \frac{{g_{1} \gamma_{1} R_{m}^{3} }}{{d^{3} }}} \right) $$
(9)
$${\tilde{\user2 E}}_{3} = f_{2} \sum\limits_{n = 1}^{\infty } {\frac{{g_{n} \varepsilon_{b} \gamma_{n} R_{m}^{2n + 1} }}{{\varepsilon_{{{\text{eff}}1}} \varepsilon_{{{\text{eff}}2}} d^{2n + 4} }}\frac{{ - \mu^{2} (\rho_{11} - \rho_{22} )}}{{\hbar [\omega - \omega_{12} + G(\rho_{11} - \rho_{22} ) + i/T_{20} ]}}\tilde{\varvec{E}}_{0} } $$
(10)
$$f_{m} = f_{2} + f_{3} $$
(11)

where \(f_{3} = - f_{2} G(\rho_{11} - \rho_{22} )/[\omega - \omega_{12} + G(\rho_{11} - \rho_{22} ) + i/T_{20} ]\), we have defined

$$G = \sum\limits_{n = 1}^{\infty } {\frac{{g_{n} \varepsilon_{b} \gamma_{n} R_{m}^{2n + 1} \mu^{2} }}{{\varepsilon_{{{\text{eff}}1}} \varepsilon_{{{\text{eff}}2}} d^{2n + 4} \hbar }}} = G_{R} + iG_{I} . $$
(12)

where G is known as the self-interaction of the SQD [8]. It arises firstly when applied field polarizes the SQD, which in turn polarizes the MNP that produces a field to interact with the SQD, and is a key in determining the shift of the frequency and enhancement of the total field felt by the SQD. Multipole effects govern the interparticle Coulomb interaction for small interparticle distance, which has been demonstrated in paper [7]. We will take N = 10 in our following calculations. As it was expected, multipole effect has crucial influence compared with N = 1 (dipole) considered for FWM response.

We can now calculate the effective susceptibility [33] of the FWM in the absence of the MNP

$$\chi_{s}^{(3)} = f_{s}^{4} \chi^{(3)} ( - 2\omega_{1} + \omega_{2} ;\omega_{1} ,\omega_{1} , - \omega_{2} ). $$
(13)

Otherwise, the effective susceptibility of the FWM in the presence of the MNP is written as

$$\chi_{m}^{(3)} = f_{m} (2\omega_{1} - \omega_{2} )f_{m}^{2} (\omega_{1} )f_{m} ( - \omega_{2} )\chi_{m}^{(3)} ( - 2\omega_{1} + \omega_{2} ;\omega_{1} ,\omega_{1} , - \omega_{2} ). $$
(14)

We directly give the expression of \(\chi^{(3)}\) corresponding to the FWM

$$\chi^{(3)} ( - 2\omega_{1} + \omega_{2} ;\omega_{1} ,\omega_{1} , - \omega_{2} ) = \frac{{ - 2i\mu N_{0} }}{{[i\hbar (\omega_{21} - 2\omega_{1} + \omega_{2} ) + \hbar \gamma_{2} ][i\hbar (\omega_{2} - \omega_{1} ) + \hbar \gamma_{1} ]}}\left[ {\frac{1}{{i\hbar (\omega_{21} - \omega_{1} ) + \hbar \gamma_{2} }} + \frac{1}{{i\hbar (\omega_{2} - \omega_{21} ) + \hbar \gamma_{2} }}} \right]. $$
(15)

For the sake of simplicity, we assume that \(\gamma_{1} = \gamma_{2} ,\) meanwhile, \(\chi_{m}^{(3)} ( - 2\omega_{1} + \omega_{2} ;\omega_{1} ,\omega_{1} , - \omega_{2} )\) has the same form with Eq. (15) as long as we make the transform \(\omega_{21} \to \omega_{21} - G_{R} (\rho_{11} - \rho_{22} )\) and \(\gamma_{1} = \gamma_{2} = 1/T_{2} \to \gamma_{m} = 1/T_{2} + G_{I} (\rho_{11} - \rho_{22} ).\) We assume T 2 is a constant and do not consider the influence of the MNP on it in this paper.

3 Results and discussion

In this section, we investigate mainly the influence of the presence of Au MNP on the FWM response from a SQD for several parameters of the hybrid system in the cases of the local response and nonlocal response of the MNP, as well as compared with each other. We pay special attention to the small interparticle distance regime, where the multipole effects play a crucial role. We take the dielectric constant of the background to be \(\varepsilon_{b} = 1.8.\) The parameters used for SQD in the calculation are chosen as \(m_{{e,{\text{CdSe}}}}^{ * } = 0.13m_{0} ,\) \(m_{{h,{\text{CdSe}}}}^{ * } = 0.45m_{0} ,\) \(m_{{e,{\text{ZnS}}}}^{ * } = 0.28m_{0} ,\) \(m_{{h,{\text{ZnS}}}}^{ * } = 0.49m_{0} ,\) \(E_{\text{band gap,CdSe}} = 1.84\;{\text{eV,}}\) \(E_{\text{band gap,ZnS}} = 3.9\;{\text{eV}}\) [27], the relaxation time \(T_{2} = 0.3\;{\text{ps}},\) conduction band offset 0.9 eV [34], \(\varepsilon_{s} = 6.2\) [35]. For the MNP, we take the plasmon frequency as \(\hbar \omega_{p} = = 8.54\;{\text{eV}}\) [11] and \(\tau = (9.3 \pm 0.9) \times 10^{15} \;\text{s}\) [36]. We describe local response with the dashed curves and nonlocal response with the solid curves throughout this paper.

The influence of initial population difference is small for certain values of chosen parameters that we can ignore, i.e., \(\rho_{11} - \rho_{22}\) is almost constant 1 in the paper. A detailed study of self-interaction G and multipole polarization in a MNP is given in paper [7], so we straightly give the results that (a) real and (b) imaginary parts of the nonlinear susceptibility \(\chi_{\text{FWM}}^{(3)}\) of the SQD corresponding to the dipole effect and multipole effect, respectively, with the change of the pumping photon energy in Fig. 2. The nonlinear susceptibility is a physical quantity that is used to determine the nonlinear polarization of a medium under the action of an applied laser field. The real part of the nonlinear susceptibility \(\chi_{\text{FWM}}^{(3)}\) describes the frequency dispersion characteristic, and the imaginary part describes the absorption characteristic of the medium with the transmission of the light according to the theory of light transmission. We assume that the electric field polarization is along z axis and the surface distance is 5 nm. To get a better insight into the multiple effect and dipole effect, we give a reference curve (green) corresponding to the case of the absence of the MNP (bare SQD). A glance at Fig. 2 shows that the center peaks redshift obviously with the appearance of the strong absorption band in the presence of MNP compared to the reference curves. This means that, plasmon–exciton interaction results the exciton energy transferred to the MNP, but also the plasmon resonance provides strong coupling to the SQD and leads to strong enhancement of the light absorption, which is greater than the energy transfer from SQD to MNP [19]. As a consequence, dispersion in SQD changes from normal dispersion in the bare SQD into the anomalous dispersion in the hybrid system, and the absorption band can be observed in Fig. 2, which has important application in optical switching and light transmission of the device, such as anomalous dispersion optical filter and dispersion compensation devices. With the increase in N, the absorption band keeps on redshift, more specifically, and the frequency shift is about 7.6 meV (3.6 meV) for N = 10 (1). Furthermore, N = 10 is enough for convergence in all the cases studied in the paper. Another important result (Fig. 2b) shows that refractive index is suppressed when taken multipole effect into account in contrast to the results in the dipole approximation. The induced field arises from the multipole effect is stronger than that from the dipole effect, which makes the more population of particle transfer, which leads a stronger absorption. In addition, we observe the dispersion and absorption curves, in the case of nonlocal response of the MNP, are different from the ones considered in the local response, which is more evident when the multipole effect is taken into account. This is due to the fact that the polarizations are very different in the local and nonlocal models. The nonlocal effects are important in the response of the MNP when the multipoles are excited. Therefore, the multipole polarization in a MNP leads to a greater change to the nonlinear response, with optical signatures of red-shifted of the center frequency and the increase in the magnitude which will be helpful for the experimental observation. We will consider multipole effect in latter calculations instead of the dipole effect in MNP.

Fig. 2
figure 2

a Real and b imaginary parts of the \(\chi_{\text{FWM}}^{(3)}\)of the SQD for considering multiple effect (black curve), dipole effect (blue curve) and absence (green curve) of MNP in the case of nonlocal response (solid curve) and local one (dashed curve). R 1 = 2.0 nm, R 2 = 2.6 nm, d s = 5 nm and R m = 10 nm are fixed

Full size image

Figure 3 shows the dependence of the dispersion and absorption on the center-to-center surface distance between the SQD and the Au MNP. We depict in detail the dispersion and absorption curves with the change of the d s when the electric polarization parallel (black curves) and perpendicular (red curves) to the major axis of the system in Fig. 3a when \(\hbar \omega = \hbar \omega_{21}\). As the center-to-center surface distance d s is increased, the change of the refraction and the absorption is relatively gentle when the electric field polarizations along x (y) axis. However, refraction index changes dramatically when the electric field polarizations along z axis, simultaneously, the maximum and the minimum values in absorption spectrum are shown. That means there exists an optimal distance for the absorption spectrum with the fixed pump phonon energy, revealing more interesting information can be obtained for the small center-to-center surface distance. Specifically, we study the characters of the dispersion and absorption with the change of continuous pump photon frequency in Fig. 3b and c, respectively, when electric field polarizations along z axis. Dispersion has a Fano shape, and absorption is strongly enhanced at a small value of d s. A symmetric peak for dispersion and a Fano shape for the absorption curves appear with the further increasing the distance between particles. Note also that the curves coincide with the one that corresponds to the case that in the absence of the MNP at very large interparticle distance (80 nm),which indicates the interaction between SQD and MNP is almost absent at that point. The position of the center frequency is shifted toward to the blue direction when considering the nonlocal response. The smaller the distance between particles is, the bigger the blueshift of the center frequency is. In other words, the nonlocal effect is important at small distance between particles where present the more strong FWM response.

Fig. 3
figure 3

a Real and imaginary parts of the \(\chi_{\text{FWM}}^{(3)}\) versus interparticle surface distances for a fixed pumping photon frequency \(\omega = \omega_{21} ,\) parallel (g = 2) or perpendicular (g = −1) polarization are considered. Real b and c imaginary parts of the \(\chi_{\text{FWM}}^{(3)}\) for several values of the interparticle surface distance: d s = 5 nm (black curve), 10 nm (red curve) 80 nm (green curve) and for the absence of MNP (black dash–dot curve). The rest parameters are R 1 = 2.0 nm, R 2 = 2.6 nm and R m = 10 nm

Full size image

We analyze the influence of the SDQ-size on the FWM response susceptibility. The shape, size and material of the SQD strongly determine both the exciton energy level and dipole moment. Figure 4 shows the data obtained for the hybrid system with R 1 = 2.0 nm (black), R 1 = 1.5 nm (red) and R 2 = R 1 + 0.6 nm when electric field polarizations along z axis. We assume fixed value of the distance between particles d s = 5 nm. Meanwhile, the dotted curves are plotted as the reference curve corresponding to the case of the bare SQD. The same behaviors of the two sets curves are that dispersion in SQD all change from normal dispersion into the anomalous dispersion and the absorption spectrum change from negative peak to the positive peak due to the appearance of the MNP. Furthermore, the position of the resonance of the curve is shifted to the low-energy side (redshift). The interaction between the SQD and MNP makes the refractive index and absorption enhance strongly for the larger core size (black curves) of the SQD in comparison with the reference curves in a certain region, by nearly a factor of 4.75 at the maximum value of the absorption peak in Fig. 4b. It is basically consistent with experimental result where the emission intensity that is a product of local field enhancement and the modified quantum efficiency is enhanced by a factor is about 4 [15]. A different behavior occurs in the smaller size core (red) that the magnitude is suppressed strongly in the presence of the MNP. This reflects the size of the SQD has significant impact on the nonlinear optical response. Using effective mass theory, we obtain the results for the larger and smaller SDQ, \(\hbar \omega_{21} = 2.2582\;{\text{eV}}\) and \(\mu = 1.2159{\text{e}}\;{\text{nm}}\) when R 1 = 2.0 nm, R 2 = 2.0 + 0.6 nm, \(\hbar \omega_{21} = 2.497\;{\text{eV}}\) and \(\mu = 0.9653{\text{e}}\;{\text{nm,}}\) when R 1 = 1.5 nm and R 2 = 1.5 + 0.6 nm, respectively. Note that, Eq. (14) describing the FWM response has an important parameter: the local field factor f m, which is determined by the self-interaction \(G \propto \mu^{2}\) in Eq. (12). The decrease in the SQD size leads to the decrease in the dipole, all these make the interplay of the SQD and MNP weaken and the induced field becomes weak. Therefore, the absorption coefficient decreases with the size of the SQD decrease; thus, the absorption still enhance strongly relative to the bare SQD. As demanded by Kramers–Kronig relations, there is a complementary behavior between the absorption and dispersion, the increase in the absorption must correspond to the decrease in the refractive index and the anomalous dispersion appears in the absorption band. We note that a blueshift of the resonance position of the curves takes place remarkably when the size of the SQD is larger in nonlocal response of the NMP.

Fig. 4
figure 4

Dispersion (real part) and absorption (imaginary part) curves are plotted as function of the pumping photon energy for different sizes of the SQD, i.e., R 1 = 2.0 nm, R 2 = 2.0 + 0.6 nm (black curves) and R 1 = 1.5 nm, R 2 = 1.5 + 0.6 nm (red curves), respectively

Full size image

Figure 5 shows dispersion and absorption characteristics with the same geometrical parameters R 1 = 2.0 nm, R 2 = 2.6 nm and d s = 5 nm but different sizes of the MNP when the electric field along the system major axis. For comparison, the nonlinear optical response for the same geometrical parameters of the hybrid structure and the polarization which is orthogonal to the major axis of the system are plotted in Fig. 6. The dash–dot curves (green) are plotted as the reference curve corresponding to the case of absence of the MNP in the Figs. 5 and 6. Figure 5 clearly reveals a substantially red-shifted of the center frequency and enhancement of the optical response from the SQD with the increase in the MNP-size. We point out that the larger size of the MNP brings in stronger plasmonic effects, which are sensitively proportional to the particle size and shape [37]. The absorption is suppressed strongly and no obvious absorption band appears in the Fig. 6, as compared to the case of a parallel polarized field. It is shown from Figs. 5 and 6 that (1) the redshift of the center frequency appear with the increase in the MNP-size, irrelevant to the direction of polarization of the electric field, (2) the enhancement of the refractive index and the absorption in comparison with the bare SQD when the electric field polarization along z axis. The situation is reverse when the electric field polarization orthogonal to the z axis, which might be due to the weakness of the induced field strongly and (3) comparing the FWM response in Figs. 5 and 6, the order of the magnitude is 10−13 and 10−15, respectively. It is agreement with the experimental data [15], and the absorption may change dramatically by nearly 2 orders in magnitude in that structure, where the maximal value along the laser polarization axis and the minimal value at the direction perpendicular to it. It is quite useful to compare the properties of these two cases of the electric filed polarization. Furthermore, we have observed that the nonlocal effects are important for the larger size of the MNP when the electric field polarization parallel to z axis; thus, the case is opposite for the electric field polarization perpendicular to z axis, where nonlocal effects is important for the smaller size of the MNP. These findings suggest that the enhancement or the suppression of the dispersion and absorption manifesting significant dependence on the polarization of the electric field and the size of the MNP in the hybrid system should be an important tuning parameter in optimizing nonlinear optical response.

Fig. 5
figure 5

Dispersion (real part) and absorption (imaginary part) curves of the SQD in the hybrid system with d s = 5 nm, R 1 = 2.0 nm and R 2 = 2.6 nm at different sizes of the MNP when the electric field polarization is parallel to the system major axis

Full size image
Fig. 6
figure 6

Same response as in Fig. 5, except here, the electric field polarization is perpendicular to the system major axis

Full size image

As far as the calculated results is concerned, we assume that the detuning of the two incident light beams with frequencies \(\omega_{1}\) and \(\omega_{2}\) is zero, i.e., \(\omega_{2} - \omega_{1} = 0.\) However, the detuning has impact on the nonlinear response. The fixed parameters \(\omega_{1} = \omega_{21} ,\) R 1 = 2.0 nm, R 2 = 2.6 nm, R m = 10 nm and d s = 5 nm are chosen. We will take into nonlocal effect account only in the size with these parameters according to the previous calculations. The FWM response of the SQD considered the nonlocal effect in the hybrid system (red curves) and the bare SQD (black curves) versus the detuning of the incident light is presented in Fig. 7. From the picture, we can see that the presence of the MNP results the dispersion and absorption curves changed in opposite directions compared with the bare SQD. Typically, absorption band blue-shifted and the absorption is enhanced strongly, and the magnitude of the absorption peak range from −1.4419 × 10−14 m2/V2 to 5.4476 × 10−16 m2/V2. This shows that the appearance of the MNP not only changes the resonance frequency but also enhances the nonlinear optical response remarkably. On the other hand, the response of SQD becomes more complicated in the hybrid system with the change of the detuning, the real and imaginary part of the FWM susceptibility indicate the presence of a satellite peak on the absorption band edge. It has been shown that there is a nonlinear frequency-dependent behavior due to the strong coupling between the SQD and the MNP.

Fig. 7
figure 7

FWM response of the SQD in the hybrid system (red) and the bare SQD (black) with the changing of the detuning between the two incident light frequency

Full size image

4 Conclusion

To summarize, the FWM of a coupled hybrid system composed of a MNP and a SQD has been studied theoretically by using the effective mass and rotating wave approximation. Dispersion and absorption characteristics of the SQD in the local and nonlocal optical response of the MNP have been presented. It has been shown that the nonlocal effect should be taken in special conditions where the stronger FWM is presented. Moreover, we have found that a strong absorption band appearance in the presence of the MNP and this enhancement can be easily tuned by varying the size of the nanoparticles and the center-to-center distance. The order of the magnitude of the enhancement factor calculated is in agreement with the experimental result. Finally, the impacts of the detuning of the two incident light beams on the nonlinear response are investigated. SQD–MNP hybrid system holds great promise for controlling nonlinear optical properties. Our results provide a new method for optimizing and controlling the nonlinear response of the SQD. It would be of great interest to extend the present calculation by considering the susceptibility of the hybrid system in which the nonlocal nature of the dielectric response may be shown greater important.