1 Introduction

The development of the chirped pulse amplification (CPA) technique enabled generation of petawatt-power optical radiation [1–3]. Superintense optical radiation has been widely used for producing monoenergetic electron and proton beams generated during the interaction of extreme light with gas and solid targets. The most significant parameters of optical radiation in such studies are peak focusing intensity, time contrast and duration. Consequently, temporal and spatial characteristics of superintense laser radiation should be optimized. Of particular interest is investigation of a possibility of using thin (less than 1 mm) optical elements for generation of second harmonic radiation aimed at increasing time contrast [4], time recompression of femtosecond pulses [5], optical polarization transformation from linear to a circular one.

The intensity of unfocused petawatt radiation is several TW/cm2. In these conditions, small-scale self-focusing (SSSF) [6] is the principal restriction in using transmission optical elements. SSSF is induced by cubic nonlinearity of the medium and leads to enhanced spatial perturbations and laser beam filamentation and, consequently, to damage of optical elements. The SSSF impact may be reduced by minimizing the accumulated nonlinear phase (B-integral), as well as by reducing spatial noise. In the first case, thin, large-aperture (~100 mm) optical elements are needed. In the second case, spatial filters—vacuum lens telescopes with a diaphragm in the focal plane—are usually employed [7–9]. The diaphragm allows suppressing perturbations with the transverse wave vectors in the instability band. These filters are efficient for nanosecond pulses with a characteristic intensity of several GW/cm2. However, such devices cannot be used for spatial filtering of powerful femtosecond radiation with TW/cm2 peak intensity as lenses greatly modify parameters of the radiation.

In the present work, we propose, justify theoretically and verify experimentally, the method in which free space is used for filtering spatial perturbations of high-intensity (~1 TW/cm2) laser beams. Here and after, free space is a vacuum free space. The method is mostly convenient to be implemented after optical vacuum compressors, and the distance between the last diffraction grating and the target chamber can be used like a spatial filter. The proposed method is applicable for radiation with intensities over several hundred GW/cm2. For lower intensities, unreasonably huge free space will have to be used. A technique of calculating a safe distance between the mirrors that are sources of noise and the transparent optical elements is considered.

2 Free space is a noise filter

We will consider a possibility of using free space as a filter of spatial perturbations of a laser beam. To begin with, we will study the dependence of the noise power amplified in a medium with cubic nonlinearity on the angle of vision of the nonlinear element and on the accumulated nonlinear phase.

The process of spatial noise (harmonic perturbations) amplification in a medium with cubic nonlinearity was considered and studied in ample detail [6]. The key parameters are the transverse wave vector of harmonic perturbation \(\mathop {k_{ \bot } }\limits^{ \to }\) and the nonlinear phase referred to as B-integral:

$$B = \frac{2\pi }{\lambda }\gamma \cdot I \cdot h, $$
(1)

where λ is wavelength, I is radiation intensity, γ is cubic nonlinearity and h is the thickness of the nonlinear medium. The characteristic values for solids are γ = (3/8) × 10−7 cm2/GW. These parameters determine the amplification coefficient of harmonic perturbations averaged over initial phases [10]:

$$G\left( {\kappa ,B} \right) = \frac{1}{2}\left( {2\cos h^{2} (Bx) + \left( {\frac{{2Bx}}{{\kappa ^{2} - 4B}}} \right)^{2} \sin h^{2} (Bx) + \left( {\frac{{\kappa ^{2} - 4B}}{{2Bx}}} \right)^{2} \sin h^{2} (Bx)} \right), $$
(2)

where \(x^{ 2} = \frac{{\kappa^{ 2} }}{B} - \frac{{\kappa^{ 4} }}{{4B^{ 2} }}\), \(\kappa = k_{ \bot } \sqrt {h/k}\) is the normalized transverse wave vector, \(k = \frac{2\pi }{\lambda }n\) is the wave vector and n is the index of refraction. The highest amplification of harmonic perturbations is attained at the following value of the wave vector \(k_{ \bot }^{\hbox{max} }\) [6, 7]:

$$\varphi_{\hbox{max} } = \frac{{k_{ \bot }^{\hbox{max} } }}{k} = \sqrt {\frac{2\gamma I}{n}} $$
(3)

The harmonic perturbations grow if their transverse wave vector inside the nonlinear medium lies within the instability band [6]:

$$0 < \frac{{k_{ \bot } }}{k} \le 2 \cdot \sqrt {\frac{\gamma I}{n}} $$
(4)

It is clear from the expressions (3, 4) that the transverse wave vectors corresponding to the maximum amplification coefficient and the instability boundary depend only on medium parameters and intensity of the intense wave. The angle between the noise wave vector and the z-axis \(\left( {\varphi \cong \frac{{k_{ \bot } }}{k}} \right)\) at which the amplification coefficient is maximal (Fig. 1) and is proportional to \(\sqrt I\). In glass with refractive index n = 1.5 and nonlinearity γ = 3.35 × 10−7 cm2/GW, this angle is φ max = 1.2 mrad for the powerful wave intensity 3 GW/cm2 and φ max = 36.6 mrad 3 TW/cm2. As the “dangerous” angles for intense radiation (3 TW/cm2) are rather large, spatial components may be filtered in free space. Filtering of laser radiation with the intensity of several GW/cm2 demands much longer beam propagation in free space, which in turn, may be critical for beams obtained experimentally. It is important to note that this length cannot be increased by using several mirrors, as every mirror is a source of spatial noise. By increasing the distance between the last mirror in front of the transparent optical element, it is possible to decrease the amplitude of laser beam harmonic perturbations in the region of a strong impact of cubic nonlinearity. The idea of the proposed method is illustrated in Fig. 1. If the angle of vision θ = D/L is much smaller than φ max, then a substantial part of noise will be outside the nonlinear element aperture and, hence, will not be amplified in it. Noise appearing on reflection at the preceding mirrors or diffraction gratings will be suppressed still more as the noise sources are located farther from the nonlinear element.

Fig. 1
figure 1

Schematic diagram of using free space for filtering spatial harmonic perturbations

Full size image

Let us now consider amplification of the power of spatial harmonics of beam perturbations in a medium with cubic nonlinearity. To provide uniform noise power distribution at the input, noise at the output of the nonlinear medium may be written in the form

$$\frac{{P_{{n\_out}} }}{{P_{{n\_in}} }} = \frac{{\int_{\Omega } {G\left( {\overrightarrow{k}_{ \bot } ,B} \right)d^{2} \overrightarrow{k}_{ \bot } } }}{{\int_{\Omega } {d^{2} \overrightarrow{k}_{ \bot } } }} = \frac{{2 \cdot \int\limits_{0}^{{\chi _{{\max }} }} {G\left( {\kappa ,B} \right)\kappa d\kappa } }}{{\chi _{{\max }}^{2} }} $$
(5)

Here, Ω is the domain of integration in the wave vector space, \(\chi_{\hbox{max} } = \frac{{\theta \sqrt {h \cdot k} }}{{n\sqrt {\left( {4 + \theta^{2} } \right)} }}\) is the maximum dimensionless transverse wave vector defined by the Snell’s law and the angle of vision \(\theta = \frac{D}{L}\), where D is beam diameter and L is the distance from the noise source to the nonlinear element. Formula (5) takes into account that the harmonic perturbations with transverse wave vector κ > χ max make an insignificant contribution to the output noise power. The safe angle of vision of the nonlinear element must be less than angle θs found from the condition \(\chi_{\hbox{max} } = \sqrt {2 \cdot B}\) (see Eq. 4):

$$\theta_{\rm s} = \frac{{n\sqrt {8 \cdot B} }}{{\sqrt {hk - 2Bn^{2} } }} = \sqrt {\frac{8\gamma In}{1 - 2\gamma In}} $$
(6)

when θ ≪ θ s, the well-amplified harmonic perturbations are filtered by free space, thus reducing the risk of optical element damage, even at large values of B-integral. The smaller the angle of vision, the more safely is to use any transparent optical elements. The dependence of θ s versus intensity for the observed parameters is depicted in Fig. 2.

Fig. 2
figure 2

The dependence of the angle of vision θ s mrad versus intensity, the safety region is θ ≪ θ s

Full size image

The technique of calculation of safety distance between the source of spatial noise and the transmission optical element is to calculate the θ s angle for the prospective level of intensity, which is going to be used in experiments, and chose the distance from the condition L ≫ D/θ s. For example, if the beam parameters are I = 1 TW/cm2, D = 100 mm the safety distance L should be significantly more 1.6 m.

Note that components of the harmonic perturbations with transverse wave vectors \(\left( {\kappa \ll \sqrt {2 \cdot B} } \right)\) cannot be omitted within the framework of the proposed technique. The worst situation in terms of SSSF development is when the angle of vision overlaps the instability band where all the dangerous components are in the region of a strong field and are well amplified. Relative position of the transmission element and the noise source in this region has almost no impact on the power of the amplified noise.

3 Experimental results and discussion

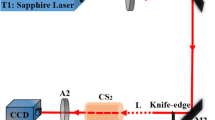
To confirm a possibility of using free space as a spatial filter of laser beam perturbations, we developed a vacuum chamber combined with a compressor of the front end of the femtosecond laser complex PEARL [1]. The schematic diagram of the experiment is shown in Fig. 3. The compressor output radiation passed through a narrowing mirror telescope with astigmatism correction (magnification f 2 /f 1  = 0.3, where f 1,2 are the focal distances of spherical mirrors), and propagated through the noise source to a nonlinear medium. A dielectric mirror was the source of spatial perturbations of intense laser radiation, and a 4 mm-thick parallel-sided plate made of K8 glass was the nonlinear medium. A system controlling parameters of the radiation comprised a femtosecond pulse duration meter (second-order intensity autocorrelator), as well as energy, beam profile and frequency spectrum meters. Pulse duration was measured before and after the experimental runs. Control of the duration of each pulse was complicated by the need to use a transmission optical element dividing plate which, at the intensity of several TW/cm2, strongly modifies radiation parameters, such as phase and spectral intensity. All transmission optical elements, which were used for diagnostics of the beam parameters, were shifted out from the beam line in the experiments with B-integrals more than 5.

Fig. 3
figure 3

Schematic diagram of the experiment on studying a possibility of using free space for filtration of harmonic perturbation. Here, AW-automated fused silica wedge 1 mm, SM1 and SM2 are spherical mirrors of a narrowing telescope, SN—source of spatial noise, 1 first reflection from the wedge for spectrum control (out of vacuum chamber), 2 s reflection from the wedge for near field control (out of vacuum chamber)

Full size image

Laser pulse energy (1–20 mJ) and distance between the nonlinear element and the source of spatial noise were measured in our experiment. The radiation intensity distribution in the Fresnel zone (in the plane of the nonlinear medium) is shown in Fig. 4. The peak intensity of output radiation for this profile was 3.6 TW/cm2 at pulse energy 20 mJ and duration FWHM 70 fs. The central wavelength of the radiation was 910 nm. The pulse repetition rate of the front end was 1 Hz.

Fig. 4
figure 4

Intensity distribution in the Fresnel zone

Full size image

No damage was observed in the glass sample on a single exposure to such a pulse, despite the value of B-integral exceeded 20 for the peak intensity. However, on multiple exposure (10–100 pulses), the transmission coefficient in the sample decreased and pronounced brown spots appeared in the sample (see Fig. 5a). A darker imprint of the laser pulse corresponded to a more developed instability of harmonic perturbations. Plots of the transmission coefficient of the nonlinear element exposed to 100 laser pulses normalized to the transmission coefficient of its undamaged part as a function of radiation wavelength are presented in Fig. 5b for different angles of vision. The difference between the transmission coefficients of damaged and undamaged glass was greatest at the border between the ultraviolet and visible parts of the spectrum. This, in turn, explains the brown color of the laser beam imprints. The considered effect became stronger at large angles of vision (θ = 0.13), as harmonic perturbations with maximum increment were present in the region of strong influence of cubic nonlinearity and were amplified efficiently. The decrease of the angle of vision resulted in spatial filtration of harmonic perturbations. In this case, the SSSF process was insignificant even for the B-integral of 20.

Fig. 5
figure 5

a Photo of the glass sample after experimental runs; b Experimental plots of the normalized spectral transparency of K-8 glass exposed to 100 laser pulses as a function of radiation wavelength for different angles of vision

Full size image

This conclusion is fully confirmed by Fig. 6 where one can see the experimental points and the theoretical dependence of the logarithm of normalized amplified noise power as a function of the calculated value of B-integral and angle of vision. The noise power was normalized to the calculated value at the experimental point labeled by a square. There are three types of the experimental points on the diagram: black, gray and white. The points were obtained after exposure of the sample by 100 laser pulses. The color of the points corresponds to the transmission coefficient in the visible spectral range: black points correspond to bad transmission (serious damage), gray ones correspond to average transmission (moderate damage) and white circles correspond to no damage at all. The theoretical isolines demonstrate the equal conditions for the amplification of the noise power. Normalized logarithm of noise power is shown next to each isoline. The isoline passing throw the square point divides the diagram into two parts, which determines safety and dangerous areas of parameters for implementation of the transmission glass plate. The square point was chosen from experimental data. In the safety region, the experimental points have no damages and were white colored on the diagram. The brown imprints were observed in the dangerous area, and experimental points are gray and black.

Fig. 6
figure 6

Theoretical curves: logarithm of noise power normalized to the value at a point labeled by a square as a function of B-integral and angle of vision. Experimental points: black, gray and white circles correspond to high, small and zero transmission reduction due to optical damage

Full size image

The value of B-integral was calculated for peak intensity of the laser radiation. It is important to emphasize the difference between results of exposure of the medium to picosecond or nanosecond pulses and to intense femtosecond radiation. In the first case, there regularly arise tracks in the nonlinear element despite smaller values of the B-integral, while no apparent tracks have been observed for femtosecond radiation, even for the B-integral more than 20.

The several experimental facts justify the explanation of the phenomena: the peak intensity of the laser beam was not changed crucially in the different positions of the nonlinear element; the observed structure of the imprints in microscope demonstrated that the diameter of the small spots is about several microns; the distribution of the spots on the brown imprints has no preferred spatial structure and the damages distributed homogenously across the area of the beam.

It is worth noting that the presented result is the first experimental confirmation of the principle of spatial noise filtration using free space for laser beams with the intensity of several TW/cm2. For the values of the B-integral exceeding 10, radiation parameters are strongly modified—the frequency spectrum broadens appreciably and acquires strong modulation and the spatial beam distribution becomes strongly inhomogeneous. Hence, the proposed approach of using free space as a filter of harmonic perturbations allows avoiding damage of transmission optical elements, but does not eliminate other negative effects caused by cubic nonlinearity.

4 Conclusion

To conclude, we have proposed to use free space for filtering harmonic perturbations of laser beams having intensity of several TW/cm2 instead of vacuum spatial filters. The method was supported by the linearized theoretical model of SSSF development in media with cubic nonlinearity and was verified experimentally. The proposed technique allows using transmission optical elements for petawatt beams, which greatly expands capabilities of controlling their parameters: efficient conversion to the second harmonic, circular polarization or controlled spectrum broadening for subsequent recompression.