1 Introduction

In lidar observations, background noise may generate spurious signals that can adversely affect measurement accuracy. Consequently, the appropriate treatment of such background noise is an important element of lidar data processing, but debate continues regarding the most effective approach, and different researchers use different techniques. Some determine the level of background noise experimentally by placing a cover over the telescope of the lidar system [1]. However, the background noise signal obtained in this manner is simply electronic noise and does not include background noise generated by the atmosphere. An alternative approach uses the average value of three data points acquired prior to laser shots, or the value of distant data points, as the background noise level [2–4]. However, in this method, the background noise level obtained is not real, because significant fluctuations of electronic noise exist in the signal. In fact, the multi-averaged value of fluctuating electronic noise is negligibly small. Background noise generated by the atmosphere depends on the wavelength of the lidar, which should be constant, independent with distance [5, 6]. Two factors affect the background noise value: the width of the band-pass filter used and the measurement time. In the case of a wide band-pass filter and daytime measurements, background noise levels may be very large and independent of altitude. Researchers commonly reduce background noise levels experimentally by making lidar measurements at night, using a narrow band-pass filter, and decreasing the telescope’s field of view [7]. Even so, it remains difficult to determine the level of atmospheric background noise. Few papers have considered in detail how to obtain background noise levels, but here we present a method that facilitates the detection of larger background noise levels based on the shape of the range-corrected signal, and an approach to calculating background noise levels from the measurement data. In case of fine day (or just after raining) lidar observation, the lidar range-corrected signal should be smooth without any aerosol loading. In general case, in lower altitude (or boundary layer), the atmosphere is dirty with more aerosols loading, and in higher altitude, the atmosphere is clear or with less aerosol loading. Anyway, we can always find any ranges (long or short) where the range-corrected signal is smooth, due to clear atmosphere or homogenous aerosol layer. In this paper, an equation that describes background noise in a clear atmosphere or homogeneous aerosol layer is derived in detail, and the background noise level is calculated using experimental data and a simulated lidar signal.

2 Theoretical analysis of background noise

2.1 Identifying the presence of larger background noise levels

In lidar data analysis, the range-corrected signal (P(r) × r 2) is the intensity of lidar signal multiplied by r 2. The numerical value of range-corrected signal is much larger than lidar return signal, easy to find the fine structure of lidar signal. The shape of range-corrected signal can be used to easily find inhomogeneous atmospheric layers, clear atmospheric or homogenous aerosol layers where the lidar return signal is small but range-corrected signal is more strong. Therefore, the shape of the range-corrected signal can be used to easily identify a clear atmosphere or homogeneous aerosol layer. At high altitude, the atmosphere is clearer than that in the aerosol layer at lower altitudes and is also homogeneous. According to the shape of range-corrected signal, we can find some homogeneous layers (some ones are thick and some ones are thin) where range-corrected signal is smooth and extinction coefficients is almost constant. To demonstrate the characteristics of a range-corrected signal containing a large amount of background noise, we performed the simulations shown in Fig. 1, which show three overlapping simulated lidar signals, with clear atmosphere or homogeneous aerosol layer from 4,000 to 8,400 m between two aerosol layers. One of the signals is a simulated lidar signal with no background noise, while the other two are simulated lidar signals with background noise levels of 1e−7 and 2e−7. At around 3,400 and 8,800 m, we assume two thick aerosol layers existence there. The background noise effect is taken into consideration in the whole range.

Fig. 1
figure 1

a Three overlapping simulated lidar signals, one without background noise and two with background noise levels of 1e−7 and 2e−7. b Range-corrected signals corresponding to a with homogeneous layer from 4, 000 to 8,400 m between two aerosol layers

Full size image

It can be difficult to distinguish lidar signals having different background noise levels, such as those in Fig. 1a. However, the use of range correction allows signals containing more background noise to be identified, such as in Fig. 1b, which shows the range-corrected signals corresponding to Fig. 1a. In Fig. 1b, we selected two points \(\left( {Q(r_{1} ) = p_{1} r_{1}^{2} ,Q(r_{2} ) = p_{2} r_{2}^{2} } \right)\) \(\left( {(p_{1} + \Updelta p)r_{1}^{2} ,(p_{2} + \Updelta p)r_{2}^{2} } \right)\) in the range-corrected signal without background noise (with background noise at \(\Updelta p = 2{\text{e}}^{ - 7}\)) in the homogeneous layer. According to the lidar equation, we have

$$P(r) = KP_{0} \frac{A}{{r^{2} }}\beta (r)\exp \left[ { - 2\int\limits_{0}^{r} {\alpha (r){\text{d}}r} } \right] $$
(1)

Here, P(r), P 0, β(r), and α(r) are the lidar return signal, laser power, backscatter coefficient, and extinction coefficient, respectively, while r, K, and A are distance, the lidar constant, and the telescope area, respectively. According to Fig. 1b and Eq. (1), we consider the background noise calculation as follows. Rayleigh scattering and extinction relates to the value of temperature, pressure, and wavelength [8]. Regard of all the factors, the Rayleigh scatter coefficient and extinction is calculated, according to reference 8, as in Fig. 2. Figure 2a–d shows the backscatter coefficient (β(r)) at 532 nm, extinction coefficient α(r) at 532 nm, the integral calculation of extinction coefficient \(\left( {\int_{0}^{r} {\alpha (r){\text{d}}r} } \right)\), and the backscatter coefficient multiplied by attenuation \(\left( {\exp ( - 2\int_{0}^{r} {\alpha (r){\text{d}}r} } \right)\).

Fig. 2
figure 2

a Rayleigh backscatter coefficient profile at 532 nm. b Rayleigh extinction coefficient profile at 532 nm. c Integral calculation of extinction coefficient at 532 nm. d Backscatter coefficient multiplied by attenuation

Full size image

We set two points at r 1 and r 2 in Figs. 1b, 2d, respectively. Equation (2) is satisfied. By Fig. 2d, it is easy to have Eq. (3). In consideration of Eqs. (1), (2), and (3), we obtain Eq. (4).

$$r_{1} \le r_{2} $$
(2)
$$\beta (r_{1} )\int\limits_{0}^{{r_{1} }} {\alpha (r){\text{d}}r} > \beta (r_{2} )\int\limits_{0}^{{r_{2} }} {\alpha (r){\text{d}}r} $$
(3)
$$P_{1} r_{1}^{2} > P_{2} r_{2}^{2} $$
(4)

Now, considering a range-corrected signal with an assumed background noise of Δp, P 1, and P 2 is function of range r 1 and r 2, we have

$$(P_{1} + \Updelta p)r_{1}^{2} > (P_{2} + \Updelta p)r_{2}^{2} $$
(5)

The physical meaning of (5) is when background noise is small, the range-corrected signal also decays, similar to the situation of the range-corrected signal without background noise. In case of small background noise, the justification of background noise existence is difficult and rearranging gives

$$\frac{{P_{1} r_{1}^{2} - P_{2} r_{2}^{2} }}{\Updelta p} > r_{2}^{2} - r_{1}^{2} $$
(6)

When Δp is small, Eq. (6) is satisfied, while when Δp is large enough, Eqs. (7) and (8) will be satisfied, that is,

$$\frac{{P_{1} r_{1}^{2} - P_{2} r_{2}^{2} }}{\Updelta p} < r_{2}^{2} - r_{1}^{2} $$
(7)
$$(P_{1} + \Updelta p)r_{1}^{2} < (P_{2} + \Updelta p)r_{2}^{2} $$
(8)

In this case, Eqs. (7) and (8) describe the increasing range-corrected signal in the clear atmosphere or homogeneous aerosol layer, and the background noise concealed within the lidar signal is large, that is, \(\Updelta p = 2{\text{e}}^{ - 7} > 1{\text{e}}^{ - 7}\), as shown in Fig. 1b. The physical meaning of (8) is the shape of increasing range-corrected signal can contain a large amount of background noise concealed in lidar signal.

2.2 Calculation of background noise level

Rearranging Eq. (1) gives Eq. (9)

$$Q_{0} (r) = P(r)r^{2} = KAP_{0} \beta (r)\exp \left[ { - 2\int\limits_{0}^{r} {\alpha (r){\text{d}}r} } \right]. $$
(9)

Regarding a lidar signal without background noise, Eq. (9) calculated at r 1 and r 2 gives

$$Q_{0} (r_{1} ) = P(r_{1} )r_{1}^{2} = KAP_{0} \beta (r_{1} )\exp \left[ { - 2\int\limits_{0}^{{r_{1} }} {\alpha (r){\text{d}}r} } \right], $$
(10)

and

$$Q_{0} (r_{2} ) = P(r_{2} )r_{2}^{2} = KAP_{0} \beta (r_{2} )\exp \left[ { - 2\int\limits_{0}^{{r_{2} }} {\alpha (r){\text{d}}r} } \right] $$
(11)

or

$$\ln \frac{{Q_{0} (r_{1} )}}{{KAP_{0} \beta (r_{1} )}} = \ln \frac{{P(r_{1} )r_{1}^{2} }}{{KAP_{0} \beta (r_{1} )}} = \ln \left[ {P(r_{1} )r_{1}^{2} } \right] - \ln [KAP_{0} ] - \ln \beta (r_{1} ) = - 2\int\limits_{0}^{{r_{1} }} {\alpha (r){\text{d}}r} , $$
(12)

and

$$\ln \frac{{Q_{0} (r_{2} )}}{{{\text{KAP}}_{0} \beta (r_{2} )}} = \ln \frac{{P(r_{2} )r_{2}^{2} }}{{{\text{KAP}}_{0} \beta (r_{2} )}} = \ln [P(r_{2} )r_{2}^{2} ] - \ln [{\text{KAP}}_{0} ] - \ln \beta (r_{2} ) = - 2\int\limits_{0}^{{r_{2} }} {\alpha (r){\text{d}}r} . $$
(13)

We then subtract Eq. (12) from (13) to obtain

$$\ln [P(r_{2} )r_{2}^{2} ] - \ln [P(r_{1} )r_{1}^{2} ] - \ln \beta (r_{2} ) + \ln \beta (r_{1} ) = - 2\int\limits_{0}^{{r_{2} }} {\alpha (r){\text{d}}r} + 2\int\limits_{0}^{{r_{1} }} {\alpha (r){\text{d}}r} , $$
(14)

which can be rearranged to give

$$\Updelta (\ln Q_{0} (r)) = \Updelta (\ln [P(r)r^{2} ]) = \ln \frac{{\beta (r_{2} )}}{{\beta (r_{1} )}} - 2\int\limits_{{r_{1} }}^{{r_{2} }} {\alpha (r){\text{d}}r} . $$
(15)

Considering a lidar signal with background noise Δp, we have

$$\Updelta (\ln [Q_{N} (r) - \Updelta Q]) = \Updelta (\ln [(P(r) - \Updelta P)r^{2} ]) = \ln \frac{{\beta (r_{2} )}}{{\beta (r_{1} )}} - 2\int\limits_{{r_{1} }}^{{r_{2} }} {\alpha (r){\text{d}}r} . $$
(16)

where Q N (r) means range-corrected signal with background noise, N represent background noise.

This can be rewritten as

$$\Updelta (\ln [(P(r) - \Updelta P)r^{2} ]) = \ln \frac{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }}{{(P(r_{1} ) - \Updelta P)r_{1}^{2} }} = \ln \frac{{\beta (r_{2} )}}{{\beta (r_{1} )}} - 2\int\limits_{{r_{1} }}^{{r_{2} }} {\alpha (r){\text{d}}r} , $$
(17)

or

$$\Updelta (\ln [(P(r) - \Updelta P)r^{2} ]) = \ln \frac{{(P(r_{3} ) - \Updelta P)r_{3}^{2} }}{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }} = \ln \frac{{\beta (r_{3} )}}{{\beta (r_{2} )}} - 2\int\limits_{{r_{2} }}^{{r_{3} }} {\alpha (r){\text{d}}r} . $$
(18)

Equations (18) − (17) gives (19),

$$\ln \frac{{(P(r_{3} ) - \Updelta P)r_{3}^{2} }}{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }} - \ln \frac{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }}{{(P(r_{1} ) - \Updelta P)r_{1}^{2} }} = \ln \frac{{\beta (r_{1} )\beta (r_{3} )}}{{\beta (r_{2} )\beta (r_{2} )}} + 4\int\limits_{0}^{{r_{2} }} {\alpha (r){\text{d}}r} - 2\int\limits_{0}^{{r_{3} }} {\alpha (r){\text{d}}r - 2\int\limits_{0}^{{r_{1} }} {\alpha (r){\text{d}}r} } $$
(19)

In the case of

$$\Updelta r = r_{2} - r_{1} = r_{3} - r_{2} ,$$

We define \(f_{1} (r_{2} ) = \ln \frac{{\beta (r_{1} )\beta (r_{3} )}}{{\beta (r_{2} )\beta (r_{2} )}}\) and \(f_{2} (r_{2} ) = 4\int_{0}^{{r_{2} }} {\alpha (r){\text{d}}r} - 2\int_{0}^{{r_{3} }} {\alpha (r){\text{d}}r} - 2\int_{0}^{{r_{1} }} {\alpha (r){\text{d}}r}\) at ∆r = constant.

Therefore, we have

$$\ln \frac{{(P(r_{3} ) - \Updelta P)r_{3}^{2} }}{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }} - \ln \frac{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }}{{(P(r_{1} ) - \Updelta P)r_{1}^{2} }} = f_{1} (r_{2} ) + f_{2} (r_{2} ) = f(r_{2} ). $$
(20)

For easy discussion, we do Rayleigh (clear atmosphere) calculation for \(f_{1} (r_{2} ),f_{2} (r_{2} )\,{\text{and}}\,f(r_{2} )\) as shown in Fig. 3.

Fig. 3
figure 3

a Function of \(J(r_{2} ) = \frac{{\beta (r_{1} )\beta (r_{3} )}}{{\beta (r_{2} )\beta (r_{2} )}}\) calculated at \(\Updelta r = 38.7\)m. b Function of \(f_{1} (r_{2} ) = \ln J(r_{2} )\) and \(f_{2} (r_{2} ) = 4\int_{0}^{{r_{2} }} {\alpha (r){\text{d}}r} - 2\int_{0}^{{r_{3} }} {\alpha (r){\text{d}}r} - 2\int_{0}^{{r_{1} }} {\alpha (r){\text{d}}r}\) calculated at \(\Updelta r = 38.7\) m. c Function of \(f(r_{2} ) = f_{1} (r_{2} ) + f_{2} (r_{2} )\)

Full size image

In Fig. 3a, it is easy to see that \(J(r_{2} ) = \frac{{\beta (r_{1} )\beta (r_{3} )}}{{\beta (r_{2} )\beta (r_{2} )}} \approx 1\) at \(\Updelta r = 38.7\) m. Fig. 3b shows \(f_{1} (r_{2} ) = \ln J(r_{2} ) = \ln \frac{{\beta (r_{1} )\beta (r_{3} )}}{{\beta (r_{2} )\beta (r_{2} )}} \approx 0\) and \(f_{2} (r_{2} ) = 4\int_{0}^{{r_{2} }} {\alpha (r){\text{d}}r} - 2\int_{0}^{{r_{3} }} {\alpha (r){\text{d}}r} - 2\int_{0}^{{r_{1} }} {\alpha (r){\text{d}}r \approx 0}\). Figure 3c is the sum of \(f_{1} (r_{2} )\) and \(f_{2} (r_{2} )\), it is obviously shown that \(f(r_{2} ) = f_{1} (r_{2} ) + f_{2} (r_{2} ) \approx 0\). Figure 3 shows that \(f(r_{2} )\) is negligibly small at any altitude, r 2. In case of a homogeneous aerosol layer, we can assume \(\beta (r)\) and \(\alpha (r)\) are constant, obviously, \(f_{1} (r_{2} ) = 0\), \(f_{2} (r_{2} ) = 0\) and \(f(r_{2} ) = f_{1} (r_{2} ) + f_{2} (r_{2} ) = 0\) exist. Therefore, in case of clear atmosphere (Rayleigh scatter) or homogeneous aerosol layer, we have

$$\ln \frac{{(P(r_{3} ) - \Updelta P)r_{3}^{2} }}{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }} - \ln \frac{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }}{{(P(r_{1} ) - \Updelta P)r_{1}^{2} }} = f(r_{2} ) \approx 0. $$
(21)

Rearrange Eq. (21) to obtain Eq. (22),

$$\frac{{(P(r_{3} ) - \Updelta P)r_{3}^{2} }}{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }} = \frac{{(P(r_{2} ) - \Updelta P)r_{2}^{2} }}{{(P(r_{1} ) - \Updelta P)r_{1}^{2} }} $$
(22)

Expanding Eq. (22) gives

$$(P(r_{1} )P(r_{3} ) - (P(r_{1} ) + P(r_{3} ))\Updelta P + \Updelta^{2} P)\frac{{r_{1}^{2} r_{3}^{2} }}{{r_{2}^{4} }} = P^{2} (r_{2} ) - 2P(r_{2} )\Updelta P + \Updelta^{2} P, $$
(23)

And, for easy discussion, replacing \(\frac{{r_{1}^{2} r_{3}^{2} }}{{r_{2}^{2} }}\) with k, we obtain

$$\Updelta^{2} P + \frac{{2P(r_{2} ) - k(P(r_{1} ) + P(r_{3} ))}}{k - 1}\Updelta P + \frac{{kP(r_{1} )P(r_{3} ) - P^{2} (r_{2} )}}{k - 1} = 0. $$
(24)

To obtain the background noise level Δp, we take the inverse of Eq. (24). During the calculation, k depends on the range r 1, r 2, r 3 related to the selected points (in next section). Aerosol loading relates to the backscatter and extinction coefficient β(r) and α(r) in Eq. (1). It is easily to see lidar return signal P(r) results from aerosol loading in Mie lidar measurements. If no aerosol loading, the Mie lidar return signal will be zero. Aerosol loading would not disturb the background noise calculation. For easy calculation, we assume the aerosol loading is homogeneous at high altitude; actually, the inhomogeneous aerosol loading at lower altitude does not affect the background noise calculation results.

3 Treatment of randomness thermal and electric noise signal

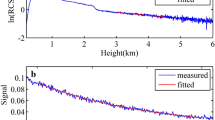
The background noise includes background light noise from the atmosphere and thermal and electric noise from detector and lidar system. The background light noise from atmosphere depends on the used wavelengths can be taken as constant [5, 6]. Usually, according to empirical experiment, the thermal and electric noise is randomness, and empirical average of randomness noise is constant, independent of range. Figure 4 is the background noise taken from our lidar system.

Fig. 4
figure 4

Background noise from lidar system

Full size image

In Fig. 4, the random noise including sky background is taken from the running lidar system. The laser beam is blocked and telescope is opened. In this case, the detected signal consists of thermal and electric noise from the detector and operation lidar system and background noise from sky. Table 1 presents the sky background. We can see the sky background radiation relates to the associated wavelength. Generally, interference filter associated with used wavelength is used in lidar system, and the background noise from sky should be constant [5, 6]. We do linear fit calculation for the random noise, as shown in Fig. 4. Combination of Fig. 4 and Table 1 indicates that the averaged randomness noise is almost constant, independent with range.

Table 1 Sky background radiation [5, 6, 9]
Full size table

4 Calculating background noise using experimental data

We applied this theoretical approach to the calculation of background noise levels in experimental data at 532 nm, as shown in Fig. 5. The lidar return and range-corrected signals are arbitrary unit. Figure 5a shows the lidar return signal beyond 2,000 m is very small. Three overlapping lidar signals are shown in Fig. 5a, the original signal (black line) without noise treatment and two signals with a small background noise element with values of −0.00437 (blue) and −0.00483 (red). For easy discussion, we present the range-corrected signal (P(r)*r 2) in Fig. 5b, which is the lidar return signal (P(r)) amplified by r 2. Figure 5b shows the range-corrected signal between 2,000 and 5,000 m clearly. Figure 5b is an enlarged view of the signals in Fig. 5a, shown with an expanded y-axis. In Fig. 5b, we have selected five points (①–⑤) in the homogeneous layer (3,000–4,000 m) from the original lidar signal, where the range-corrected signal in Fig. 5c is smooth.

Fig. 5
figure 5

a Three overlapping lidar signals: the original signal (black line) without background noise treatment and two with background noise treatment at values of −0.00437 (blue) and −0.00483 (red). b The lidar signals in a shown on an expanded y-axis. c Range-corrected signals corresponding to a

Full size image

The range and signal intensity of the five points are listed in Table 2.

Table 2 Parameters for ΔP calculation
Full size table

In Table 2, points ①, ③, and ⑤, and points ②, ③, and ④, are used to calculate the background noise levels in the two signals. Points ①, ③, and ⑤ have ranges of r 1 = 3,006 m, r 2 = 3,500.75 m, and r 3 = 3,995.5 m, respectively, and satisfy the condition Δr = r 3 − r 2 = r 2 − r 1 = 494.75 m and signal intensities of P 1 = 0.0223, P 2 = 0.001164, and P 3 = 0.00558, respectively. For points ②, ③, and ④, the three ranges are r 1 = 3,103.45 m, r 2 = 3,500.75 m, and r 3 = 3,898.05 m, respectively, and they satisfy the condition \(\Updelta r = r_{3} - r_{2} = r_{2} - r_{1} = 397.30\) m. The signal intensities are P 1 = 0.01992, P 2 = 0.001164, and P 3 = 0.00646, respectively. The observed range bins r 1, r 2, r 3 can be selected automatically at condition of \(\Updelta r = r_{3} - r_{2} = r_{2} - r_{1}\) in homogeneous aerosol layer. Inserting these parameters for points ①, ③, and ⑤, and points ②, ③, and ④, into Eq. (22), we obtain background noise values of ΔP = − 0.00483, and ΔP = − 0.00437, respectively. Similar noise levels were obtained from the two groups, that is, \(\Updelta P = - 0.00483 \approx - 0.00437\). The background noise values of −0.00483 or −0.00437 were then subtracted from the original measurement signal to obtain two lidar signals or range-corrected signals. Figure 5b, c show that the original signal and the range-corrected signal (black lines) are negative at high altitude (>4,500 m), but after background noise treatment, the two range-corrected lidar signals become positive (blue and red) and are almost equal and overlapping.

Figure 6 also shows a lidar signal and is similar to Fig. 5, but in Fig. 6 the signal intensity at high altitude is positive. We selected six points (①–⑥) from the lidar signal (black line) in the homogeneous layer (3,500–5,000 m) where the range-corrected signal (Fig. 6c) is smooth. For points ①, ③, and ⑤, the range and intensity are r 1 = 3,500.75 m, r 2 = 4,003 m, and r 3 = 4,505.25 m, while P 1 = 0.00998, P 2 = 0.00605, and P 3 = 0.00438, respectively, and satisfy the condition \(\Updelta r = r_{3} - r_{2} = r_{2} - r_{1} = 502.25\,{\text{m}}\). For points ②, ④, and ⑥, the range and intensity are r 1 = 3,748.13 m, r 2 = 4,302.85 m, and r 3 = 4,857.57 m, while P 1 = 0.00758, P 2 = 0.00493, and P 3 = 0.00387, respectively, and satisfy the condition \(\Updelta r = r_{3} - r_{2} = r_{2} - r_{1} = 554.72\) m. As in the calculation in Fig. 5, inserting the parameters (range and signal intensity) for points ①–⑥ into Eq. (22), we obtain the background noise levels for points ①, ③, and ⑤, and points ②, ④, and ⑥, of ΔP = 0.00301 (blue), and ΔP = 0.00308 (red), respectively. The lidar signals and range-corrected signals treated with the background noise correction are almost equal and overlap completely (Fig. 6).

Fig. 6
figure 6

a Three overlapping lidar signals. b Lidar signals in a shown with an expanded y-axis. c Range-corrected signals

Full size image

Comparing Figs. 5 and 6, we find that the calculated background noise is negative in Fig. 5 and positive in Fig. 6. At high altitudes, the original range-corrected signal is clearly negative (Fig. 5c), and the range-corrected signal adjusted for the background noise becomes positive and larger than the original. In Fig. 6c, at high altitude, the original range-corrected signal is positive and decays, and the range-corrected signal adjusted for the background noise is also positive and decays, but is smaller than the original.

5 Calculating background noise in a simulated lidar signal

Figure 7 shows simulated lidar signals for which the background noise level has to be calculated. Figure 7a shows the simulated lidar signals, with and without background noise, which are shown on an expanded y-axis in Fig. 7b. Points 1, 2, 3, and 4 were selected from the simulated lidar signal with background noise (Fig. 7b), with ranges of 6,000, 7,000, 8,000, and 9,000 m and signal intensities of 7.5467e−6, 5.49071e−6, 4.1705e−6, and 3.27508e−6, respectively. We again used Eq. (22) to calculate the background noise based on the parameters (range and intensity) from two groups of points (1–3 and 2–4) and obtained the same background noise level for each: \(\Updelta P = 2{\text{e}} - 7\). We subtracted this background noise (\(\Updelta P = 2{\text{e}} - 7\)) from the upper lidar signal (red) to obtain the lower lidar signal (black) without background noise (Fig. 7b).

Fig. 7
figure 7

a Simulated lidar signals. b Lidar signals in a shown on an expanded y-axis. c Range-corrected signals

Full size image

To further verify Eq. (22), we also selected four points (①–④) from the lower signal in Fig. 7b, with ranges of 6,500, 7,500, 8,500, and 9,500 m and intensities of 6.1973e−6, 4.56295e−6, 3.48213e−6, and 2.73244e−6, respectively. Inserting the same parameters as previously from the two groups (①, ②, ③, and ②, ③, ④) into Eq. (22), we obtained background noise levels of −3.39142e−10 ≪ e−6 and 9.799e−11 ≪ e−6, that is, negligibly small.

Figures 5, 6 show the background noise calculation results from experimental data, and Fig. 7 is background noise level calculation by using simulation data. The calculation results in Figs. 5, 6 coincide with that in Fig. 7. The physical meaning of this work is to be able to obtain more precisely the background noise concealed in lidar data. Before lidar data analysis, we should do background noise calculation, so that we can remove background noise from the raw lidar data to make the lidar measurement data more real, more comparable, more reliable. Otherwise, we cannot know the background accurately, and the lidar measurement results will be questionable. This work can ensure lidar data with high quality in meteorological studies.

6 Conclusions

In lidar measurements, the level of background noise generated by the atmosphere is related to the wavelengths used and can be treated as constant. In a homogeneous atmospheric layer, an increasing range-corrected signal indicates that larger background noise levels are concealed within the lidar measurement data. In this paper, we developed a theoretical background noise calculation using parameters (range and intensity) from equally spaced reference points in the lidar signal. Testing this theoretical approach, we found that reasonable background noise levels were obtained using parameters derived from experimental data, and the accuracy of the background noise level was calculated using a simulated lidar signal. These calculations, based on parameters from measured and simulated signals, verified our theoretical approach to the assessment of background noise levels in lidar data.