1 Introduction

Plasmonic waveguide structures (i.e. photonic waveguide structures that involve metal-dielectric interfaces) have been extensively studied in recent years because they hold promise for subwavelength confinement and efficient manipulation of light at the nanoscale, see, e.g., [1–4]. The structures, however, suffer from metallic losses and consequently exhibit an inherent trade-off between confinement and propagation length [5–8]. Various geometries have been proposed and compared with the aim of improving this trade-off. Among 1-D structures, a plasmonic slot waveguide, formed by a dielectric core placed between two metallic slabs, appears to be most effective [6, 9].

Applications of plasmonic waveguides in nano-optical circuits require solution of the problem of coupling between plasmonic waveguides [10–13] as well as the problem of coupling between plasmonic and external dielectric waveguides [14, 15]. To this aim, directional couplers that involve plasmonic waves were studied both theoretically and experimentally [10–19].

Due to strong enhancement of local electromagnetic fields, nonlinear optical phenomena can be boosted in plasmonic devices. A comprehensive overview of nonlinear plasmonic effects and their main applications has been recently published in Ref. [20]. In particular, the nonlinear effects enable active control of optical signals propagating in plasmonic devices [21]. For example, efficient and fast all-optical modulation can be achieved by light-induced absorption modulation in the dielectric [22, 23] and metal [24].

This paper considers Kerr-nonlinearity (i.e. intensity dependent refractive index), which, in conjunction with plasmonics, can enable fabrication of miniature all-optical functional devices, such as switches, gates or memories. Concerning nonlinear dielectric structures, one of the simplest yet most important devices is a nonlinear directional coupler. Such couplers, in which power is periodically exchanged between two waveguides placed in close proximity, exhibit strongly nonlinear characteristics and may be utilized, e.g., for power-dependent switching [25]. Recently, similar nonlinear couplers with plasmonic waveguides have been proposed and investigated [26, 27]. Simulation results for the couplers with plasmonic slot waveguides [26, 28] indicate that metallic losses significantly decrease the coupler performance and unrealistically high nonlinearities are required for the switching operation; note, however, that the sharpness of the switching response can be recovered by using a tapered geometry [29].

The analysis in Refs. [26, 28, 29] assumes that the slot waveguides are made of nonlinear dielectric cores and linear metallic claddings. However, bulk metals may exhibit strong third-order nonlinearities at optical frequencies, see [30] and references therein. Such nonlinearities were recently considered in numerical studies of plasmonic metal film waveguides [31] and couplers [31, 32]. It is an open question whether the usual neglecting of metal nonlinearities in the case of plasmonic slot waveguides is justified.

In this paper, a numerical investigation of nonlinear coupling between plasmonic slot waveguides is presented in more detail. In particular, we discuss the effect of losses on the coupler performance and the nonlinearity levels required for the switching operation. After obtaining results for the suggested structure [26], various modifications of its parameters are considered with the aim of improving the nonlinear characteristics and decreasing the switching levels. The influence of metal nonlinearities is briefly discussed as well.

2 Analysis

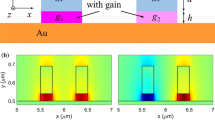
We consider a planar coupler formed by two identical plasmonic slot waveguides. The geometry of the structure is shown in Fig. 1. The structure exhibits Kerr-nonlinearity so that the dielectric function \(\varepsilon(y,z)\) can be separated into the linear, \(\varepsilon^{(0)}(y),\) and nonlinear, \(\Updelta \varepsilon(y,z),\) parts

$$\varepsilon = \varepsilon^{(0)}+\Updelta \varepsilon = \varepsilon^{(0)} + \gamma\hbox{\bf E}\cdot\hbox{\bf E}^\ast, $$
(1)

where \({\bf E}\) is the electric field, and γ is the Kerr-nonlinear coefficient. \(\varepsilon^{(0)}(y)\) and γ(y) are piecewise constant functions given by the relations \(\varepsilon^{(0)}=\varepsilon_m, \gamma=\gamma_m\) for claddings, and \(\varepsilon^{(0)}=\varepsilon_d, \gamma=\gamma_d\) for cores.

Fig. 1
figure 1

The geometry of the plasmonic coupler. The structure consists of two identical waveguides with dielectric cores and metallic claddings. The waveguide widths are w and the separation of the cores is s. \(\varepsilon_m\) and \(\varepsilon_d\) are the linear dielectric functions of the metal and the dielectric, respectively. γ m and γ d are the Kerr coefficients of the metal and the dielectric, respectively. The coupler is excited at z = 0 with the linear mode of one waveguide with the incident power P 0. P 1 and P 2 are the powers propagating in the two waveguides

Full size image

Simulation of the coupler is achieved in two steps. First, we calculate eigenmodes of the linear structure [i.e. we assume \(\Updelta \varepsilon=0\) in Eq. (1)] by using a finite-difference modesolver. Then, the unknown electric and magnetic fields of the nonlinear structure are expanded in the terms of those eigenmodes as

$$\hbox{\bf E}(y,z) = {\sum_{m}}f_m(z) {\bf e}_{m}(y)\exp{(i\omega t-i\beta_m z)}, $$
(2)
$$\hbox{\bf H}(y,z) = {\sum_{m}}f_m(z) {\bf h}_{m}(y)\exp{(i\omega t-i\beta_m z)}. $$
(3)

Here, \({\bf e}_{m}\) and \({\bf {h}}_{m}\) are the transversal electric and magnetic field profiles of the m-th eigenmode, respectively. β m is the corresponding propagation constant, ω is the angular frequency and the functions f m are the unknown modal amplitudes. Note that we consider only the modes propagating in the +z direction. As the mode profiles are orthogonal, they are normalized by using the following relation:

$$\int\limits \left({{\bf e}}_{m}\times c\mu_0{{\bf h}}_{n}\right) \cdot \user2{{\hat{\varvec{\rm\mathbf z}}}} dy= \frac{\delta_{mn}}{2}. $$
(4)

The integral is over the entire computational window in the y direction, c is the speed of light in vacuum, μ 0 is the vacuum magnetic permeability, \(\user2{{\hat{\rm\mathbf z}}}\) is the unit vector parallel to the z-axis, and δ mn is the Kronecker delta.

A standard approach based on the coupled-mode theory [33] leads to the nonlinear coupled system for the amplitudes f m

$$\frac{df_m}{dz} = -i{\sum_{n}}K_{mn}f_n\exp{\left[i(\beta_m-\beta_n) z\right]}, $$
(5)

where

$$K_{mn}=\frac{\omega}{c}\int \left(\Updelta \varepsilon {{\bf e}}_{m\bot}\cdot{{\bf e}}_{n\bot} - \frac{\Updelta \varepsilon \varepsilon^{(0)}}{\varepsilon^{(0)}+ \Updelta \varepsilon } {e}_{mz}{e}_{nz} \right) dy, $$
(6)

and \({\bf e}_{m\bot}\) denotes the transverse part of \({\bf e}_{m}.\) Note that because \(\varepsilon\) is complex, neither Eq. (4) nor Eq. (6) contains complex conjugates of the fields.

The structure is excited at z = 0 with the linear plasmon mode (i.e. the fundamental TM mode) of one of the slot waveguides, scaled to the power P 0 (Fig. 1). Kerr-nonlinearity is characterized with a parameter \(\Updelta n_{\rm{NL},0}\) defined as the maximum nonlinear index change in the dielectric core at the structure input. Note that the parameter \(\Updelta n_{\rm{NL},0}\) is proportional to the product γ d P 0 (provided that the other parameters are kept constant). The input excitation is also expanded as in Eqs. (2) and (3), thus providing initial values of f m . Then, the coupled system in Eq. (5) is solved by using the standard numerical approach, i.e Runge-Kutta technique. The following calculations were carried out with only 2 eigenmodes (symmetric and antisymmetric) used in the expansion. However, we verified that using more modes does not significantly increase accuracy of the results.

First, we discuss the effect of losses on the coupler performance. We consider the idealized structure with the numerical parameters defined by Salgueiro and Kivshar [26] (silver claddings and silica cores at a wavelength λ = 480 nm; the values of \(w/\lambda\) and \(s/\lambda\) were rounded to a single digit) and compare results for the lossless (Fig. 2a) and lossy (Fig. 2b) cases. Because the structure serves only as a model, we neglect the metal nonlinearities for the moment (γ m  = 0). We will consider a realistic value of γ m later.

Fig. 2
figure 2

a and b Relative powers P 1/P 0 and P 2/P 0 as functions of the normalized propagation distance \(z/\lambda\) for various nonlinearity levels \(\Updelta n_{\rm{NL},0}\) (the values of \(\Updelta n_{\rm{NL},0}\) in the box apply for the both graphs). a Lossless structure, \(\varepsilon_m=-8.25;\) b Lossy structure, \(\varepsilon_m=-8.25\text{--}i0.3;\) the other numerical parameters for a and b are \(\varepsilon_d=2.25, \gamma_m=0, w/\lambda=0.08\) and \(s/\lambda=0.1.\) c The normalized coupling length \(L_c/\lambda\,\) vs. the nonlinearity level \(\Updelta n_{\rm{NL},0\,}\)for various values of the normalized core separation \(s/\lambda,\) the other parameters are as in a or b

Full size image

As seen in Fig. 2a, the lossless structure exhibits behavior similar to that of the dielectric coupler [25]. Namely, power is periodically exchanged between the waveguides and two types of solutions are observed. (1) For low nonlinearity levels (low input powers), the amount of the exchanged power is equal to P 0 and the coupling length L c (defined here as a position of the first maximum of P 2) increases with \(\Updelta n_{\rm{NL},0}\) [see the curve labeled as “no losses” (\(s/\lambda=0.1\)) in Fig. 2c]. (2) If \(\Updelta n_{\rm{NL},0}\) exceeds a certain critical value (at which \(L_c\rightarrow\infty\)) the exchanged power is less than P 0 and, for sufficiently high \(\Updelta n_{\rm{NL},0},\) the power remains in the input waveguide. Transition between these two states can be used for the power-dependent switching.

This behavior changes significantly when metallic losses are taken into account, see Fig. 2b, c. The extreme values of P 1 and P 2 occur at different positions, the exchanged power is always less than P 0 and L c becomes shorter and upper limited (see the curve for \(s/\lambda=0.1\) labeled “losses” in Fig. 2c). Furthermore, the maximum of L c is shifted to the higher values of \(\Updelta n_{\rm{NL},0}\) suggesting that higher input powers are required for the nonlinear switching. Such increase of switching power was already observed [26].

Figure 3 (the curve for \(s/\lambda=0.1\)) shows the corresponding switching characteristic; in this case, the coupler length was adjusted to the coupling length L c,0 of the linear device in order to maximize P 2 at the end of the coupler. Obviously, due to the losses, the maximum of P 2 does not reach P 0.

The performance of the switching operation cannot be much improved by altering the core separation s (see Figs. 2c, 3). Decreasing s leads to a shorter linear coupling length L c,0 so the effect of losses can be almost arbitrarily minimized. However, the shorter L c,0 requires higher nonlinearity levels for the switching operation. Thus, the device exhibits a trade-off between the effect of losses (controlled by s) and the switching level of \(\Updelta n_{\rm{NL},0}\): for a given maximal achievable value of \(\Updelta n_{\rm{NL},0},\) we obtain a minimal value of s. Note that the switching levels \(\Updelta n_{\rm{NL},0} \sim 0.5\) seen in Fig. 3 (which correspond to the normalized input power ∼0.4 as defined and observed by Salgueiro and Kivshar [26]) are already extremely high.

The influence of the waveguide width w on the switching characteristics is presented in Fig. 4. It is observed that, in this case, altering w cannot improve coupler performance either. For a qualitative explanation, consider three competing mechanisms (see Fig. 5) which affect the characteristics. (1) For a plasmon mode of an individual slot waveguide with the effective mode index n eff, the propagation length \(L_{p}=\left|4\pi\rm{Im}\left(n_{\rm{eff}}\right)/\lambda\right|^{-1}\) generally increases with increasing w [9]. (2) The confinement factor (the ratio of the power inside the core to the entire power carried by the mode) of the mode decreases with increasing w. Thus, we observe a decrease of the nonlinear sensitivity \(\eta=dn_{\rm{eff}}/d\left(\Updelta n_{\rm{NL},0}\right)\) (the derivative is evaluated at \(\Updelta n_{\rm{NL},0}=0\)) of the effective mode index. (3) This is accompanied with the decreasing difference between the propagation constants of the symmetric and antisymmetric coupler eigenmodes and therefore with the increasing coupling length L c,0. The relative influence of these factors depends on other coupler parameters. For the structure under consideration, two conclusions follow from the dependencies presented in Fig. 5. First, the ratio L p /L c,0 increases with increasing w. As a result, the linear coupling efficiency (i.e. P 2/P 0 at \(\Updelta n_{\rm{NL},0}=0\) in Fig. 4) is increased with increasing w. Second, consider the phase shift \(\phi=\left(2\pi/\lambda\right)n_{\rm{eff}} L_{c,0}\) acquired over the distance L c,0. Nonlinear sensitivity \(d\phi/d\left(\Updelta n_{\rm{NL},0}\right)\propto \eta L_{c,0}\) of the shift decreases with increasing w. Thus, the switching levels of \(\Updelta n_{\rm{NL},0}\) seen in Fig. 4 increase slightly with increasing w. As we will see later, this behavior may substantially change with different values of optical constants.

Fig. 3
figure 3

Relative power P 2/P 0 vs. the nonlinearity level \(\Updelta n_{\rm{NL},0}\) for different constant values of the normalized core separation \(s/\lambda.\,P_2\)was calculated at z = L c, 0 = the coupling length of the linear device (L c,0 varies with s). The remaining parameters are as in Fig. 2b

Full size image

Now, we take into account the metal nonlinearities by assuming γ m  > 0 [30]. Numerical experiments show that all the previously presented characteristics are unaffected by the actual value of γ m provided that γ m is less than or approximately equal to γ d . Further increasing γ m causes more losses in the nonlinear case. However, for realistic structures consisting of silica and silver, γ m is three orders of magnitude larger than γ d [34]. This means that nonlinearity of silica can be neglected and the coupler completely loses its functionality.

Fig. 4
figure 4

Relative power P 2/P 0 vs. the nonlinearity level \(\Updelta n_{\rm{NL},0}\) for different constant values of the normalized waveguide width \(w/\lambda.\,P_2\) was calculated at z = L c,0 = the coupling length of the linear device (L c,0 varies with w). The remaining parameters are as in Fig. 2b

Full size image
Fig. 5
figure 5

The normalized propagation length \(L_{p}/\lambda,\) normalized coupling length \(L_{c,0}/\lambda,\) and nonlinear sensitivity η vs. the normalized waveguide width \(w/\lambda.\,L_{p}\) and L c,0 were calculated for linear structures. L p and η were calculated for plasmon mode of single slot waveguide. The other structural parameters are as in Fig. 4

Full size image

Finally, we demonstrate that the switching characteristics can be improved by changing the width of the waveguide core provided that material parameters are suitably chosen. We assume that the core is made of silicon nanocrystals (Si-nc) embedded in an amorphous silica matrix [35, 36]. For simulations (Figs. 6, 7), we supposed λ = 1.55 μm and used the linear refractive index n Si-nc = 1.54 − i10−5 of one Si-nc sample measured in Ref. [36]. For claddings, we used the dielectric function of silver [37]. These linear parameters provide propagation lengths that are longer than those in the previous simulations.

Fig. 6
figure 6

Relative power P 2/P 0 vs. the nonlinearity level \(\Updelta n_{\rm{NL},0}\) for the coupler with parameters \(\varepsilon_d=(1.54{-} i10^{ - 5})^2, \varepsilon_m= -130{-}i3.3, s/\lambda=0.05,\) and different constant values of the normalized waveguide width \(w/\lambda.\,P_2\) was calculated at z = L c,0 = the coupling length of the linear device. The characteristics are independent of value γ m provided γ m is less than or of the same order of magnitude as γ d

Full size image
Fig. 7
figure 7

The normalized propagation length \(L_{p}/\lambda,\) normalized coupling length \(L_{c,0}/\lambda,\) and nonlinear sensitivity η vs. the normalized waveguide width \(w/\lambda.\,L_{p}\) and L c,0 were calculated for linear structures. L p and η were calculated for plasmon mode of single slot waveguide. The other structural parameters are as in Fig. 6

Full size image

Si-nc exhibit a high nonlinear response and can find applications in all optical switching devices [35, 36]. Considering the data presented in Ref. [36], we estimate that γ d ∼3γ m and thus the metal nonlinearities can be safely neglected. Compared with other high nonlinear materials, the low value of n Si-nc ≈ 1.5–1.9 enables longer propagation lengths in slot waveguides. Note that this structure serves only as an example; the actual value of γ d may vary with optical intensity [36] and we also leave aside the problem of whether such materials can be integrated with current technologies.

Figure 6 presents the switching characteristics of such coupler for various constant values of the waveguide width w. (An influence of the waveguide separation s is not considered; the above-described trade-off is generally valid indeed. However, we used smaller constant value of s, with the aim of obtaining coupling efficiencies similar to those in Fig. 4.) The observed behavior can be explained with the help of Fig. 7. The ratio L p /L c,0 remains approximately constant. Thus, the linear coupling efficiency (P 2/P 0 at \(\Updelta n_{\rm{NL},0}=0\) in Fig. 6) does not vary appreciably with w. In contrast with the situation in Fig. 5, the product η L c,0 increases with increasing w. As a result, significant reduction of switching levels is achieved by increasing w (Fig. 6). Note, however, that the switching levels are still very high and the reduction is achieved at the price of a longer device.

3 Conclusions

In summary, nonlinear coupling between plasmonic slot waveguides was numerically studied. It was shown that the losses, which always appear in the plasmonic waveguides, have not only detrimental influence on coupler performance but also put constraints on minimal nonlinearity levels required for switching operation. We observed that metal nonlinearities have negligible effect on switching characteristics, provided that the third-order susceptibility of the metal is less than or of the same order of magnitude as the third-order susceptibility of the dielectric. Depending on values of optical constants, coupler performance can be improved by changing the width of the waveguide core. However, the obtained switching levels are still very high. These results indicate that, in order to fully exploit the potential of nonlinear plasmonic couplers for creation of ultra-compact nonlinear switches, novel metallic materials with low losses and novel dielectric materials with large nonlinearities are required.