1 Introduction

Since the first discovery by Yablonovitch [1] and John [2], the photonic crystals (PCs) have been attracted great attentions of researchers for their rich physics and potential applications. The conventional PC is a kind of artificial material with periodically arranged different index materials, and the magic regions named photonic band gaps (PBGs) originating from the interface of Bragg scattering also can be obtained. In the PBGs, the propagation of electromagnetic wave (EM wave) is forbidden, whatever the polarization and the propagation direction. The larger PBGs have been potentially used in various modern applications, such as PCs lasers [3], filter [4], waveguide [5], and omnidirectional reflector [6]. Recently, the metamaterials or left-handed materials have been introduced to PCs to form the tunable PBGs [7] or \({\text{zero - }}\overline{n}\) gap [8] since firstly proposed by Veselago in 1967 [9]. Thus, the PCs containing the metamaterials become a new active research area. Similar to the conventional PCs, the PCs containing the metamaterials display strong spatial dispersion, resulting in the appearance of electromagnetic band gap structure [10, 11]. The metamaterials always contains two types of materials. One is named double-negative metamaterials whose permittivity and permeability are simultaneously negative [12], the other is called single-negative metamaterials [13]. There are two kinds of single-negative metamaterials [14]. One configuration, in which the permeability is negative but the permeability is positive, gives rise to the so-called epsilon-negative (ENG) materials. The other is that the permeability is positive but the permeability is negative. In this case, the mu-negative (MNG) materials can be obtained. Moreover, the double-negative metamaterials hardly can be found in nature materials but the ENG materials always can be found easily in practical applications, such as semiconductors [15], metals [16], plasma [17–19], and superconductors [20]. Due to the ENG materials can be looked as the negative-index materials in certain condition, the EM waves propagating in the PCs composed of the ENG materials and positive-index materials have different dispersive properties compared with the conventional PCs. Up to now, the PCs containing the ENG materials have been investigated in detail. For example, Moroz [21] studied the 3D complete PBGs of face-centered-cubic (fcc) PCs in visible and the relative band gap can be as large as 10 % even if the host dielectric ε h  = 1. He found that the spheres made out of material having a Drude-like behavior of dielectric function can provide the structure with tunable PBGs. Wang et al. [22] investigated theoretically the optical properties of a 3D self-assembly of spherical-metal nanoparticles in a fcc lattice of metals with metal particles with radii of approximately 160 nm, and found that the PBGs can be obtained in near infrared and optical frequencies. They also found that the metal nanoparticles can be replaced by dielectric spheres coated with a layer of good metal (silver), which can be found even if the absorption is taken into account. Chan et al. [23] studied the properties of PBGs for different 3D PCs constructed with spheres containing a metal core or metallic coating in theory and experiment, and also discussed the stop band gaps (SBGs) in the Г-X and Г-L directions. They found that the PBGs can be obtained if the sphere filling ratio exceeds a certain minimum in the microwave regime, with the measured results in excellent agreement with the theoretical predictions. Zhang et al. [24] investigated the PBGs of different 3D PCs with spheres containing a metal or metallic coating in theory and experiment. They found that the PBGs can be obtained in any periodic structure if filling factor is larger then a threshold. They also found that the frequency and the size of the PBGs depend on the local order rather than on the symmetry or the global along range order. The ENG materials also can be used to design some special PCs devices with the MNG materials, such as omnidirectional filter [25], multiple-channeled filter [26], and omnidirectional reflector [27]. All of those designs are based on the \({\text{zero - }}\overline{n}\) gaps, which is insensitive to the change of scaling, the disorder and also independent of polarization and incidence angle. As we know, it is very difficult to obtain the ENG and MNG materials at the same time, as we fabricate the PCs devices. However, PCs containing the ENG materials can be fabricated today by several techniques [28, 29].

As mentioned above, there are few reports about the dispersive properties of 3D PCs containing the isotropic dielectric and ENG materials, but just only focused on the ENG materials in 1D or 2D PCs. On the other hand, the effective dielectric function of the ENG material always is looked as a constant. Even if the ENG material is seen as a kind of the frequency-dependent medium, the damping factor is always ignored. Thus, such kind of PC becomes a new interesting research focus. The fcc lattices can be found in the most nature real-space structure for the optical medium, which also can be looked as the most famous atomic arrangement. Moreover, the complete PBGs for the conventional 3D PCs with fcc lattices hardly can be obtained since its high symmetry [30, 31]. Therefore, the researchers are more interesting in the SBG which is the gap in the spectrum for a fixed direction of the incident light [32] in some special applications, such as beam splitter [33] and waveguide [34].

In this paper, we intend to investigate the dispersive properties of 3D PCs containing the isotropic dielectric and ENG materials with fcc lattices based on a modified PWE method. We use a Drude-like model to describe the effective dielectric function of the ENG material, and the damping factor also is considered. We also concerned the periodic structures are infinite, whose spheres with ENG materials are arranged in the dielectric background periodically with fcc lattices. The influences of relative dielectric constant, electronic plasma frequency, damping factor and filling factor on the flat band region, the first (1st) PBG and 1st SBGs above the flat band region in the Г-X and Г-L directions for the 3D PCs containing the ENG materials are discussed, respectively.

2 Computation model and numerical method

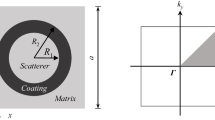
The calculated schematic of 3D PCs with fcc lattices containing the ENG materials and the first irreducible Brillouin zone for computing are plotted in Fig. 1. We assume the relative dielectric function for isotropic dielectric and ENG materials are ε a and ε p , respectively. The radius of the spheres with ENG materials and lattice constant are R and a, respectively. In the following numerical calculations, the ENG material is assumed to be isotropic and dispersive with effective dielectric function ε p can be written as [27].

Fig. 1
figure 1

Schematic structure of 3D PCs with fcc lattices and the first irreducible Brillouin zone for computing the band structures. a structure of such 3D PCs, b the first irreducible Brillouin zone for computing the band structures

Full size image
$$\varepsilon_{p} (\omega ) = \varepsilon_{b} - \frac{{\omega_{p}^{2} }}{{\omega (\omega { + }j\gamma )}} $$
(1)

where ε b , ω p , and γ are the dielectric constant of ENG material, the electronic plasma frequency and the damping factor that contribute to the absorption and losses, respectively. We compute the band structures from Maxwell’s equations by a modified PWE method as illustrated in many published papers [16, 19]. The Maxwell’s equation for the magnetic field can be expressed as:

$$\nabla \times \left[ {\frac{1}{{\varepsilon ({\mathbf{r}})}}\nabla \times {\mathbf{H}}({\mathbf{r}})} \right] = \frac{{\omega^{2} }}{{c^{2} }}{\mathbf{H}}({\mathbf{r}}) $$
(2)

where \({\mathbf{\varepsilon }}^{{{\mathbf{ - 1}}}} {\mathbf{(r)}}\) is the inverse dyadic of \({\mathbf{\varepsilon (r)}}^{{}}\). Since \({\mathbf{\varepsilon (r)}}\) is periodic, we can use Bloch’s theorem to expand the \({\mathbf{H}}\) field in term of plane wave,

$${\mathbf{H}}({\mathbf{r}}) = \sum\limits_{{\mathbf{G}}} {\sum\limits_{\lambda = 1}^{2} {h_{{{\mathbf{G}},\lambda }} {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{\varvec{\lambda}}} } e^{{\left[ {j({\mathbf{k}} + {\mathbf{G}}) \cdot {\mathbf{r}}} \right]}} } $$
(3)

where \({\mathbf{k}}\) is a wave vector in the Brillouin zone of lattice, \({\mathbf{G}}\) is a reciprocal-lattice vector, and \({\mathbf{e}}_{{\mathbf{1}}}\), \({\mathbf{e}}_{ 2}\) are orthogonal unit vectors that are both perpendicular to wave vector \({\mathbf{k + G}}\) because of the transverse character of magnetic field \({\mathbf{H}}\) (i.e., \(\nabla \cdot {\mathbf{H}} = 0\)). The dielectric constant dyadic can also be expanded into its Fourier form as,

$${\mathbf{\varepsilon }}^{{{\mathbf{ - 1}}}} {\mathbf{(r)}} = \sum\limits_{{\mathbf{G}}} {{\mathbf{\varepsilon }}^{{{\mathbf{ - 1}}}} {\mathbf{(G)}}e^{{j{\mathbf{G}} \cdot {\mathbf{r}}}} } = \sum\limits_{{\mathbf{G}}} {V_{{\mathbf{G}}} e^{{j{\mathbf{G}} \cdot {\mathbf{r}}}} } $$
(4)

where the Fourier transform coefficient \(\varepsilon^{{{ - }1}} ({\mathbf{r}})\) is also a dyadic. Substituting Eqs. (3) and (4) into Eq. (2), the following linear matrix equations can be obtained.

$$\sum\limits_{{{\mathbf{G}}^{\prime } ,\lambda^{\prime } }} {H_{{{\mathbf{G,G}}^{\prime } }}^{{\lambda ,\lambda^{\prime } }} h_{{{\mathbf{G}}^{\prime } ,\lambda^{\prime } }} } = \frac{{\omega^{2} }}{{c^{2} }}h_{{{\mathbf{G}},\lambda }} $$
(5)

where,

$$H_{{{\mathbf{G,G}}^{\prime } }}^{{\lambda ,\lambda^{\prime } }} = \left| {{\mathbf{k + G}}} \right|\left| {{\mathbf{k + G}}^{\prime } } \right|\left( {\begin{array}{*{20}c} {{\mathbf{e}}_{{\mathbf{2}}} \cdot {\mathbf{\varepsilon }}_{{{\mathbf{G,G}}^{\prime } }}^{{{\mathbf{ - 1}}}} \cdot {\mathbf{e}}_{{{\mathbf{2}}^{\prime } }} } & { - {\mathbf{e}}_{{\mathbf{2}}} \cdot {\mathbf{\varepsilon }}_{{{\mathbf{G,G}}^{\prime } }}^{{{\mathbf{ - 1}}}} \cdot {\mathbf{e}}_{{{\mathbf{1}}^{\prime } }} } \\ { - {\mathbf{e}}_{{\mathbf{1}}} \cdot {\mathbf{\varepsilon }}_{{{\mathbf{G,G}}^{\prime } }}^{{{\mathbf{ - 1}}}} \cdot {\mathbf{e}}_{{{\mathbf{2}}^{\prime } }} } & {{\mathbf{e}}_{{\mathbf{1}}} \cdot {\mathbf{\varepsilon }}_{{{\mathbf{G,G}}^{\prime } }}^{{{\mathbf{ - 1}}}} \cdot {\mathbf{e}}_{{{\mathbf{1}}^{\prime } }} } \\ \end{array} } \right) $$
(6)

To solve Eq. (5) we use the expansion Eq. (4), and write \(h_{{{\mathbf{G}},\lambda }}\) in the form

$$h_{{{\mathbf{G}},\lambda }} = \sum\limits_{{\mathbf{G}}} {A({\mathbf{k}}|{\mathbf{G}})e^{{j({\mathbf{k + G}}) \cdot {\mathbf{r}}}} } $$
(7)

As we known, the filling factor of spheres in the 3D PCs with fcc lattices is f = (16πR 3)/(3a 3). The Fourier coefficients \(V_{{\mathbf{G}}}\) could be written as [16]:

$$V_{{\mathbf{G}}} = \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\omega^{2} { + }j\gamma \omega }}{{\varepsilon_{b} \omega^{2} { + }j\varepsilon_{b} \gamma \omega - \omega_{p}^{2} }}} \right)f + \left( {\frac{1}{{\varepsilon_{a} }}} \right)(1 - f)\begin{array}{*{20}c} , & {{\mathbf{G}} = 0} \\ \end{array} } \\ {\left( {\left( {\frac{{\omega^{2} { + }j\gamma \omega }}{{\varepsilon_{b} \omega^{2} { + }j\varepsilon_{b} \gamma \omega - \omega_{p}^{2} }}} \right) - \frac{1}{{\varepsilon_{a} }}} \right) \cdot 3f\left( {\frac{{\sin (|{\mathbf{G}}|R) - (|{\mathbf{G}}|R)\cos (|{\mathbf{G}}|R)}}{{(|{\mathbf{G}}|R)^{3} }}} \right)\begin{array}{*{20}c} , & {{\mathbf{G}} \ne 0} \\ \end{array} } \\ \end{array} } \right. $$
(8)

When Eq. (8) is substituted into Eq. (5), we obtain as the equation for the coefficients {\(A({\mathbf{k}}|{\mathbf{G}})\)}

$$\begin{gathered} \left( {\left( {\frac{{\omega^{2} { + }j\gamma \omega }}{{\varepsilon_{b} \omega^{2} + j\gamma \varepsilon_{b} \omega - \omega_{p}^{2} }}} \right) (1 - f )+ \left( {\frac{1}{{\varepsilon_{a} }}} \right)f} \right) \cdot \left| {{\mathbf{k}}{ + }{\mathbf{G}}} \right|\left| {{\mathbf{k}}{ + }{\mathbf{G}}^{\prime } } \right| \cdot \overleftrightarrow {\mathbf{F}} \cdot A({\mathbf{k}}|{\mathbf{G}}) \hfill \\ + \sum\limits_{{{\mathbf{G}}_{{}}^{'} }} {^{\prime } } \left( {\left( {\frac{1}{{\varepsilon_{a} }}{ - }\left( {\frac{{\omega^{2} { + }j\gamma \omega }}{{\varepsilon_{b} \omega^{2} { + }j\varepsilon_{b} \gamma \omega - \omega_{p}^{2} }}} \right)} \right)3f\left( {\frac{{\sin (|{\mathbf{G}}|R) - (|{\mathbf{G}}|R)\cos (|{\mathbf{G}}|R)}}{{(|{\mathbf{G}}|R)^{3} }}} \right)} \right) \cdot \left| {{\mathbf{k}}{ + }{\mathbf{G}}} \right|\left| {{\mathbf{k}}{ + }{\mathbf{G}}^{\prime } } \right| \cdot \overleftrightarrow {\mathbf{F}} \cdot A({\mathbf{k}}|{\mathbf{G}}) = \frac{{\omega^{2} }}{{c_{{}}^{2} }}A({\mathbf{k}}|{\mathbf{G}}) \hfill \\ \end{gathered} $$
(9)

where the prime on the sum over \({\mathbf{G}}_{{}}^{'}\) indicates that the term with \({\mathbf{G}}_{{}}^{'} = {\mathbf{G}}_{{}}^{{}}\) is omitted. We consider \(\overleftrightarrow {\mathbf{F}} = \left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{{\mathbf{2}}} \cdot {\mathbf{e}}_{{{\mathbf{2}}^{{\mathbf{'}}} }} } & { - {\mathbf{e}}_{{\mathbf{2}}} \cdot {\mathbf{e}}_{{{\mathbf{1}}^{{\mathbf{'}}} }} } \\ { - {\mathbf{e}}_{{\mathbf{1}}} \cdot {\mathbf{e}}_{{{\mathbf{2}}^{{\mathbf{'}}} }} } & {{\mathbf{e}}_{{\mathbf{1}}} \cdot {\mathbf{e}}_{{{\mathbf{1}}^{{\mathbf{'}}} }} } \\ \end{array} } \right]\). At this point we use the definition of a complex variable \(\mu\) given by

$$\mu = \frac{\omega }{c} $$
(10)

where c is light speed in vacuum, and Eq. (8) yields

$$\mu^{4} \overleftrightarrow {\mathbf{\rm I}} - \mu^{3} \overleftrightarrow {\mathbf{T}} - \mu^{2} \overleftrightarrow {\mathbf{U}} - \mu \overleftrightarrow {\mathbf{V}} - \overleftrightarrow {\mathbf{W}} = 0 $$
(11)

where \({\mathbf{I}}\) is the identity matrix, and:

$$\overleftrightarrow {\mathbf{T}}({\mathbf{G}}|{\mathbf{G}}^{'} ) = - j\frac{\gamma }{c}{\varvec{\delta}}_{{{\mathbf{G}} \cdot {\mathbf{G}}^{'} }} , $$
(12a)
$$\overleftrightarrow {\mathbf{U}}({\mathbf{G}}|{\mathbf{G}}^{\prime } ) = \left\{ {\frac{{\omega_{p}^{2} }}{{\varepsilon_{b} c^{2} }} + \left( {\frac{1}{{\varepsilon_{b} }}f + \frac{(1 - f)}{{\varepsilon_{a} }}} \right) \cdot \left| {{\mathbf{k}}{ + }{\mathbf{G}}} \right|\left| {{\mathbf{k}}{ + }{\mathbf{G}}^{\prime } } \right| \cdot {\mathbf{F}}} \right\}{\varvec{\delta}}_{{{\mathbf{G}} \cdot {\mathbf{G}}^{'} }} + \left( {\frac{1}{{\varepsilon_{b} }} - \frac{1}{{\varepsilon_{a} }}} \right)\overleftrightarrow {\mathbf{M}}, $$
(12b)
$$\overleftrightarrow {\mathbf{V}}({\mathbf{G}}|{\mathbf{G}}^{\prime } ) = \left\{ {j\frac{\gamma }{c}\left( {\frac{1}{{\varepsilon_{b} }}f + \frac{(1 - f)}{{\varepsilon_{a} }}} \right) \cdot \left| {{\mathbf{k}}{ + }{\mathbf{G}}} \right|\left| {{\mathbf{k}}{ + }{\mathbf{G}}^{\prime } } \right| \cdot \overleftrightarrow {\mathbf{F}}} \right\}{\varvec{\delta}}_{{{\mathbf{G}} \cdot {\mathbf{G}}^{'} }} + j\frac{\gamma }{c}\left( {\frac{1}{{\varepsilon_{b} }} - \frac{1}{{\varepsilon_{a} }}} \right)\overleftrightarrow {{\mathbf{M}},} $$
(12c)
$$\overleftrightarrow {\mathbf{W}}({\mathbf{G}}|{\mathbf{G}}^{\prime } ) = \left\{ { - \frac{{\omega_{p}^{2} }}{{c^{2} }}\frac{( 1- f)}{{\varepsilon_{b} \varepsilon_{a} }} \cdot \left| {{\mathbf{k}}{ + }{\mathbf{G}}} \right|\left| {{\mathbf{k}}{ + }{\mathbf{G}}^{\prime } } \right| \cdot \overleftrightarrow {\mathbf{F}}} \right\}{\varvec{\delta}}_{{{\mathbf{G}} \cdot G^{\prime } }} { + }\frac{{\omega_{p}^{2} }}{{c^{2} }}\left( {\frac{1}{{\varepsilon_{b} \varepsilon_{a} }}} \right)\overleftrightarrow {\mathbf{M}}, $$
(12d)

where \(\overleftrightarrow {\mathbf{M}} = 3f\left( {\frac{{\sin (|{\mathbf{G}}|R) - (|{\mathbf{G}}|R)\cos (|{\mathbf{G}}|R)}}{{(|{\mathbf{G}}|R)^{3} }}} \right) \cdot \left| {{\mathbf{k}}{ + }{\mathbf{G}}} \right|\left| {{\mathbf{k}}{ + }{\mathbf{G}}^{{\mathbf{'}}} } \right| \cdot \overleftrightarrow {\mathbf{F}}\), the element of the N × N matrices are \(\overleftrightarrow {\mathbf{T}}\), \(\overleftrightarrow {\mathbf{U}}\), \(\overleftrightarrow {\mathbf{V}}\), and \(\overleftrightarrow {\mathbf{W}}\). This polynomial form can be transformed into a linear problem in 4 N dimension by \(\overleftrightarrow {\mathbf{Q}}\) that fulfills

$$\overleftrightarrow {\mathbf{Q}}z = \mu z,\,\,\overleftrightarrow {\mathbf{Q}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\overleftrightarrow {\mathbf{I}}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\overleftrightarrow {\mathbf{I}}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\overleftrightarrow {\mathbf{I}}} \\ {\overleftrightarrow {\mathbf{W}}} & {\overleftrightarrow {\mathbf{V}}} & {\overleftrightarrow {\mathbf{U}}} & {\overleftrightarrow {\mathbf{T}}} \\ \end{array} } \right] $$
(13)

Then, we can also obtain the complete solution to this 3D PCs by solving Eq. (13).

3 Results and discussion

As we know, a symmetric set of primitive vectors for the fcc lattice is a 1  = (0.5a, 0.5a, 0), a 2  = (0, 0.5a, 0.5a), a 3  = (0.5a, 0, 0.5a). The reciprocal-lattice vector basis can be defined as b 1  = (2π/a, 2π/a, −2π/a), b 2  = (−2π/a, 2π/a, 2π/a), b 3  = (2π/a, −2π/a, 2π/a). The high symmetry points have the coordinate as Г = (0, 0, 0), X = (2π/a, 0, 0), W = (2π/a, π/a, 0), K = (1.5π/a, 1.5π/a, 0), L = (π/a, π/a, π/a), and U = (2π/a, 0.5π/a, 0.5π/a). The convergence accuracy is better than 1 % for the lower energy bands as a total number of 729 plane waves can be used [35]. In order to simplify our case, we consider ε b  = 1. Without loss of generality, we plot ωa/2πc with the normalization convention ω p0 a/2πc = 1. With this definition, we can let a take any value as long as R is shifted according to achieve the same filling factors. Thus, we can define the electronic plasma frequency as ω p  = 0.35ω p0 to make the problem scale-invariant, and we also choose the damping factor as γ = γ o  = 0.02ω p , ε a  = 13.9, µ a  = 1, and µ p  = 1, respectively. Here, we only focus on the properties of 1st PBG and the 1st SBGs above the flat band region in the Г-X and Г-L directions for such 3D PCs. In order to investigate the dispersive properties of 3D PCs, the relative bandwidth is defined as

$$\Updelta \omega /\omega_{i} = 2 (\omega_{\text{up}} - \omega_{\text{low}} ) / (\omega_{\text{up}} { + }\omega_{\text{low}} ) $$
(14)

where \(\omega_{\text{up}}\) and \(\omega_{\text{low}}\) are the upper and lower limits of a PBG, respectively.

The dispersion curves for such 3D PCs with different electronic plasma frequency, damping factor and f = 0.6, respectively, are plotted in Fig. 2. The red and blue shaded regions indicate PBG and SBGs, respectively. As shown in Fig. 2a, there are two SBGs in the Г-X and Г-L directions can be observed as ω p and γ are null (the ENG materials can be seen as air), which are indicated by A and B. They present themselves at 0.3256−0.4080(2πc/a), and 0.3950−0.4019(2πc/a) in the frequency region, respectively. The 1st PBG also can be observed, which covers 0.6308−0.6321(2πc/a). As the ENG materials are introduced to the 3D PCs, the edges of such two SBGs and PBG shift to higher frequencies, and a new flat band region appears. The region of flat band spans 0−0.35(2πc/a). The main reason for flat band formation is that surface plasma waves are presented with localized fields around an ENG material sphere same as surface plasmon polaritons in the notation of metallic PCs [36]. In the flat bands, the group velocity is slow. There exist the flat band regions because of the existence of surface plasmon modes, and the plasmon resonance bands are around the cutoff frequencies of the ENG materials. The positions of two SBGs are located at 0.4211−0.4748 (2πc/a) and 0.4666−0.4675 (2πc/a), respectively. The 1st PBG runs 0.6631−0.6805 (2πc/a). Obviously, the edges of SBGs and PBG are upward to higher frequencies, and the bandwidth of PBG is enlarged but bandwidths of SBGs are narrowed. Consequently, inclusion of ENG materials in the 3D PCs with fcc lattices can not only bring a new flat band region, but also the frequency range of 1st PBG directions can be enlarged and 1st SBGs the Г-X and Г-L directions are narrowed.

Fig. 2
figure 2

The band structure of EM waves for such 3D PCs with ε a  = 13.9 and f = 0.6 but with different electronic plasma frequency and damping factor. a ω p  = 0, γ = 0, b ω p  = 0.35ω p0 , γ = 0.02ω p , and c the details of position B. The red shaded region indicates PBG, and the blue shaded regions indicate SBGs

Full size image

In Fig. 3, we plot the effects of relative dielectric constant on 1st PBG and 1st SBGs above the flat band region in the Г-X and Г-L directions for such 3D PCs with ω p  = 0.35ω p0 , f = 0.6, and γ = 0.02ω p , respectively. The shaded region indicates the PBG. As shown in Fig. 3a, the edges of 1st PBG for 3D PCs with fcc lattices are downward to lower frequencies with increasing ε a . The bandwidth of PBG increases first and then decreases with increasing the ε a . If the ε a  < 10, there is no PBG and 1st PBG will be closed at ε a  = 60. It also can be seen from Fig. 3b that the both edges of 1st SBGs in the Г-X and Г-L directions for 3D PCs shift downward to lower frequencies, and there are close points for 1st SBGs in the both directions. The bandwidths also are decreased with increasing the ε a. It is noticed that the bandwidth of SBG in the Г-L direction is obviously larger than that in the Г-X direction. As we know, the bandwidths of the PBGs are governed by refractive contrast for the PCs and the positions of the PBGs are governed by the average refractive index of the PCs. Thus, the 1st PBG for such 3D PCs can be tuned by the ε a . As shown in Fig. 3c, the relative bandwidth for the SBG in the Г-L direction is decreased with increasing the ε a , but that for the SBG in the Г-X direction is increased. A general trend for 1st PBG is the bandwidth increases first then decreases with increasing the ε a . The maximum \(\Updelta \omega /\omega_{i}\) of 1st PBG and 1st SBGs in the Г-X and Г-L directions are 0.036, 0.007, and 0.158, which can be found at ε a  = 35, 60 and 5, respectively. As mentioned above, the 1st PBG and 1st SBGs in the Г-X and Г-L directions for such 3D PCs with fcc lattices can be tuned by the relative dielectric constant of background dielectric, and the maximum \(\Updelta \omega /\omega_{i}\) for the PBG and the SBGs always appear at low-ε a regions.

Fig. 3
figure 3

The effects of relative dielectric constant on 1st PBG and 1st SBGs above the flat band region in the Г-X and Г-L directions for such 3D PCs with ω p  = 0.35ω p0 , f = 0.6 and γ = 0.02ω p , respectively. a 1st PBG, b 1st SBGs in the Г-X and Г-L directions and c relative bandwidths. The shaded region indicates the PBG

Full size image

In Fig. 4, we display the 1st PBG and 1st SBGs above the flat band region in the Г-X and Г-L directions for such 3D PCs versus f with ω p  = 0.35ω p0 , γ = 0.02ω p and ε a  = 13.9, respectively. It can be seen from Fig. 4a that the edges of 1st PBG for PCs are upward to higher frequencies with increasing the filling factor. If the f is larger than 0.49, the PBG appears. The frequency range of 1st PBG runs from 0.6936 to 0.7260 (2πc/a), and frequency bandwidth is 0.1331(2πc/a), when the f is increased from 0.49 to 0.65. Compared to f = 0.49, the bandwidth is increased by 0.1311(2πc/a). The main reason is that increasing the filling factor of ENG material means the space averaged dielectric constant becoming lower [37], and the refractive contrast for such 3D PCs is also changed. As we know, if the filling factor is equal to zero, such 3D PCs become a dielectric block. Obviously, this is a contradiction in the definition of the PCs. If the filling factor is less than 0.49, there is no PBG. In order to obtain the PBG, the filling factor needs to be greater than 0.49 as shown in the Fig. 4a. Therefore, the filling factor is an important parameter for such 3D PCs. In order to investigate the effects of the filling factor on the flat band region, we plot the band diagrams of such 3D PCs in Fig. 5 with f = 0.01, 0.1, 0.5, and 0.6, respectively. As shown in Fig. 5a, if filling factor is equal to 0.01, such 3D PCs can be approximately seen as dielectric block. The EM waves can easily propagate through the 3D PCs. Thus, the flat band region spans from 0.0542 to 0.35 (2πc/a). As shown in Fig. 5a–d, the upper edge of flat band region does not change but the area of flat band region can be tuned by the filling factor when the filling factor is small enough. As shown in Fig. 4b, the edge and central frequencies of 1st SBGs in the Г-X and Г-L directions shift upward to higher frequencies, and the bandwidths are enlarged. It is also noticed that the bandwidth for 1st SBG in the Г-L direction is larger than that in the Г-X direction. It is seen from Fig. 4c that a general trend for 1st SBG in the Г-L direction is the \(\Updelta \omega /\omega_{i}\) almost linearly increases with increasing the f but that in the Г-X direction decreases. The \(\Updelta \omega /\omega_{i}\) for 1st PBG is increased with increasing the f, if the f is larger than 0.49. The maximum \(\Updelta \omega /\omega_{i}\) of 1st PBG and 1st SBGs above the flat band region in the Г-X and Г-L directions are 0.046, 0.007, and 0.135, which can be found at f = 0.65, 0.65, and 0.30, respectively.

Fig. 4
figure 4

The effects of filling factor on 1st PBG and 1st SBGs above the flat band region in the Г-X and Г-L directions for such 3D PCs with ω p  = 0.35ω p0 , ε a  = 13.9 and γ = 0.02ω p , respectively. a 1st PBG, b 1st SBGs in the Г-X and Г-L directions and c relative bandwidths. The shaded region indicates the PBG

Full size image
Fig. 5
figure 5

The band diagrams for such 3D PPCs with ω p  = 0.35ω p0 , ε a  = 13.9 and γ = 0.02ω p but with different filling factor, a f = 0.1, b f = 0.01, c f = 0.5, and d f = 0.6, respectively. The red shaded regions indicate the PBGs

Full size image

Figure 6 shows the dependences of dispersive properties of such 3D PCs on electronic plasma frequency with ε a  = 13.9, f = 0.6, and γ = 0.02ω p0 , respectively. The shaded region indicates the PBG. As shown in Fig. 6a, the PBG can be modulated by electronic plasma frequency obviously. The edges and central frequency of 1st PBG shift upward to higher frequencies with increasing the ω p /ω p0 . The frequency range of PBG is enlarged with increasing the ω p /ω p0 . If the ω p /ω p0 <0.01, there does not exist the PBG, and such PBG will be increased with the ω p /ω p0 . Figure 6b reveals that the edges of 1st SBGs above the flat band region in the Г-X and Г-L directions are upward to higher frequencies, and a general trend for the SBG in the Г-L direction is the bandwidth decreases with increasing the ω p /ω p0 . However, the bandwidth for that in the Г-X direction increases first then decreases. As shown in Fig. 6b, the bandwidth for 1st SBG in the Г-L direction is larger than that in the Г-X direction. As shown in Fig. 6c, the general trends for 1st SBGs in the Г-X and Г-L directions are the \(\Updelta \omega /\omega_{i}\) almost decrease with increasing the ω p /ω p0 , and the relative bandwidth of 1st PBG is increased with increasing the ω p /ω p0 . The maximum \(\Updelta \omega /\omega_{i}\) of 1st PBG and 1st SBGs in Г-X and Г-L directions are 0.034, 0.016, and 0.227, which can be found at ω p /ω p0  = 0.6, 0.01 and 0.01, respectively.

Fig. 6
figure 6

The effects of electronic plasma frequency on 1st PBG and 1st SBGs above the flat band region in the Г-X and Г-L directions with ε a  = 13.9, f = 0.6 and γ = 0.02ω p0 , respectively. a 1st PBG, b 1st SBGs in the Г-X and Г-L directions and c relative bandwidths. The shaded region indicates the PBG

Full size image

In Fig. 7, we plot the effects of damping factor on the 1st PBG and 1st SBGs above the flat band region in the Г-X and Г-L directions for such 3D PCs with ω p  = 0.35ω p0 , ε a  = 13.9, and f = 0.6, respectively. The shaded region indicates the PBG. The horizontal axis of Fig. 7 is in log scale. Figure 7a shows that the edges of 1st PBG for the 3D PCs with ENG materials hardly can be tuned by the damping factor. The frequency range of 1st PBG remains invariant, and the central frequency also cannot be tuned with increasing the γ/γ o . The similar conclusion also can be obtained from Fig. 7b. The edges and central frequencies of 1st SBGs in the Г-L and Г-X directions remain invariant with increasing the γ/γ o . The bandwidths of those SBGs run from 0.4211 to 0.4748 (2πc/a), from 0.4666 to 0.4675 (2πc/a), and the bandwidths of two SBGs are 0.0009 and 0.0537 (2πc/a), respectively, as the γ/γ o is increased from 0.002 to 0.2. It can be seen from Fig. 7c that the relative bandwidths of 1st PBG and 1st SBGs in the Г-L and Г-X directions for such 3D PCs cease to change with increasing the γ/γ o . The \(\Updelta \omega /\omega_{i}\) for 1st PBG and 1st SBGs in the Г-L and Г-X directions are 0.026, 0.119, and 0.026, respectively. It is noticed that the \(\Updelta \omega /\omega_{i}\) for 1st PBG is less than that for 1st SBG in Г-L direction, and the 1st SBG in Г-L direction has the largest relative bandwidth. As mentioned above, the damping factor has no effect on the dispersive properties for 3D PCs containing the ENG materials.

Fig. 7
figure 7

The effects of damping factor on 1st PBG and 1st SBGs above the flat band region in the Г-X and Г-L directions for such 3D PCs with ω p  = 0.35ω p0 , ε a  = 13.9 and f = 0.6, respectively, a 1st PBG, b 1st SBGs in the Г-X and Г-L directions, and c relative bandwidth. The shaded region indicates the PBG

Full size image

Finally, we investigate the influence of the parameters of such 3D PCs on the upper edge of flat band region. In Fig. 8, we plot the dependences of the upper edge of flat band region for such 3D PCs on the ε a , f, ω p , and γ, respectively. As shown in Fig. 8a, b, d, the upper edge of flat band region cannot be tuned by the relative dielectric constant, filling factor and damping factor, and its location is almost unchanged with increasing the relative dielectric constant, filling factor and damping factor, respectively, the reason being that the upper edge of flat band region is around the ω p because of the existence of surface plasmon modes. Obviously, changing ε a , f and γ have no effects on the cutoff frequency of the ENG material, respectively. Thus, the cutoff frequency of the ENG material cannot be changed, and the coupling between the ENG material spheres are also unchanged. It can be seen in Fig. 8c that the upper edge of flat band region will be increased linearly with increasing the ω p /ω p0 . This is because the higher surface plasmon modes can be widely extended through the interface between the ENG material spheres with increasing the ω p . As mentioned above, the upper edge of flat band region for such 3D PCs cannot be manipulated by any parameters except for the electronic plasma frequency.

Fig. 8
figure 8

The dependences of upper edge of flat band region for such 3D PCs with ENG materials on the ε a , f, ω p , and γ, respectively. a ε a , b f, c ω p and d γ

Full size image

4 Conclusions

In summary, the dispersion properties of 3D PCs with fcc lattices containing the ENG materials for EM waves have been theoretically studied by a modified PWE method. Such modified PWE method can be used to calculate the band structures of 3D dispersive PCs with any lattices. The results show that the edge frequencies of 1st PBG and 1st SBGs above the flat band region in the Г-L and Г-X directions for such 3D PCs shift downward to lower frequencies with increasing the relative dielectric constant, and the bandwidths are enlarged first then narrowed. The bandwidths of 1st SBGs in the Г-L and Г-X directions are narrowed. The relative bandwidth of 1st PBG increases first then decreases, and the maximum \(\Updelta \omega /\omega_{i}\) for the PBG always appears at low-ε a region. The relative bandwidth of 1st SBG in the Г-L direction decreases with increasing the relative dielectric constant but that in the Г-X direction is opposite. It is also can seen that the edges of 1st PBG and 1st SBGs in the Г-L and Г-X directions for such 3D PCs shift upward to higher frequencies with increasing the electronic plasma frequency, and bandwidths also can be controlled. The larger filling factor means the larger bandwidths of 1st PBG but smaller frequencies ranges of 1st SBGs in the Г-L and Г-X directions, and their relative bandwidths almost are increased linearly with increasing the filling factor. However, changing damping factor has no effect on dispersion properties of the proposed 3D PCs. The upper edge of flat band region for such 3D PCs cannot be tuned by any parameters except for the electronic plasma frequency, and is increased linearly with increasing the electronic plasma frequency. It is also noticed that the frequency range and relative bandwidth of 1st SBG in the Г-L direction are larger than those in the Г-X direction. These results may provide theoretical instructions to design the future optoelectronic and communications devices containing the ENG materials.