Generation of femtosecond double pulse by adjusting the refractive index modulation of volume holographic grating

Abstract

Based on the modified Kogelnik’s coupled-wave theory, expressions of diffraction field distribution of volume holographic grating (VHG) are derived when it is illuminated by an ultrashort pulse. It is found that the diffracted pulse is involved into two pulses, and the two-pulse interval is found to be proportional to the refractive index modulation of the VHG. Moreover, the emergence of double pulses is periodic. An overmodulation effect of refractive index modulation of transmitted VHG is used to explain this particular diffraction behavior of the VHG. Results of our study provide a feasible method to generate interval adjustable double pulse with a simple system.

1 Introduction

With the development and maturation of ultrashort pulse laser technology, ultrashort pulses are widely used in optical communications, optical information processing and nonlinear optics. Femtosecond pulse, with ultrashort pulse durations and ultrahigh peak intensities, is becoming a powerful tool to reveal the interaction between light and materials [1, 2]. It is well known that short pulse duration means a wide spectral range; therefore, the spectral resolution is limited in femtosecond laser pump-probe measurement. If the ultrashort pulse is shaped into pulse sequences, the resolution can be improved accordingly [3–5]. Moreover, femtosecond double pulses are useful in many fields, such as coherent control of quantum states and femtosecond micromachining, etc. [3–10]. In femtosecond pulse measurement, such as Spectral Phase Interferometer for Direct Electrical-Field Reconstruction (SPIDER) and Frequency-resolved optical Gating(FROG), double pulses are also quite necessary [11–13].

The common method to generate femtosecond double pulse is by autocorrelator. A semireflecting mirror is generally used as the beam splitter, which invariably introduces material dispersion and absorption [14]. As a result, the intensities of the generated two pulses are not equal exactly, and the beam splitter has even been as thin as 2 μm in some experiments to avoid the material dispersion [15]. Therefore, a full-reflective structure to replace the semireflective mirror would be much desired. Li et al. [16] proposed a scheme using two reflective Dammann gratings to split the incident pulses. This scheme can generate multiple beams with equal intensities while avoiding both material dispersion and angular dispersion, which is a better solution than the autocorrelator scheme. Dai et al. [17] demonstrated a scheme named Dammann second harmonic-generation frequency-resolved optical gating (SHG-FROG), where three low-density reflective Dammann gratings are used. This structure can not only generate two output pulses the same as that of input pulse, but also can characterize the femtosecond pulse. Zheng et al. [18] proposed a very simple structure with two different line-density reflective gratings for pulse compression and generation of double pulses. No reflective mirror is needed. By selecting appropriate periods of gratings, this scheme can be considered as a compressor or a stretcher. Collinear double pulses are useful in femtosecond pulse measurement. Bai et al. [19] proposed a scheme where three low-density Dammann grating and two mirrors are used for the generation of collinear double pulses. This structure is free of angular dispersion and spectral spatial walk-off. In addition, this structure can also compress the positive chirped pulse, which cannot be realized with an autocorrelator structure. Liu et al. [20] proposed a structure using three Dammann gratings to generate double pulses with variable intervals, equivalent intensity and time duration. Wu et al. [21] demonstrated a scheme of using two high-density transmitted gratings for generation of double pulses. This device provides an interesting approach for conversion between single and double laser pulses.

In this paper, based on the Kogelnik’s coupled-wave theory [22] and Fourier Transform theory, we propose a new scheme to generate femtosecond double pulses by adjusting the refractive index modulations of transmitted VHG. Comparing to other schemes, our scheme needs only one volume grating with very simple structure. Using the overmodulation effect of refractive index modulation in transmitted VHG, we present a reasonable explanation on the periodic emergence of the diffracted double pulses. The relation between the pulse interval and the refractive index modulation is also discussed.

2 Theory analysis

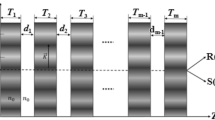
The configuration for writing and readout of a VHG is shown in Fig. 1, which is a typical transmitted VHG write-read geometry. Two copolarized cws write beams at a wavelength of λ _p incident on the surface of the photorefractive material with equal angles θ _p to record an unslanted photorefractive grating. The grating has the form of $n = n_{0} + \Updelta n\cos (Kx)$, where n ₀ is the background refractive index of the photorefractive material, Δn is the maximum refractive index modulation and $K = 2\pi /\Uplambda$ is the grating vector length with the grating period $\Uplambda = {{\lambda_{\text{p}} } \mathord{\left/ {\vphantom {{\lambda_{\text{p}} } {2\sin \theta_{\text{p}} }}} \right. \kern-0pt} {2\sin \theta_{\text{p}} }}$. In order to ensure that the recorded grating is a thick grating, the grating thickness should satisfy $d \ge 10{\kern 1pt} {\kern 1pt} n_{0} {\kern 1pt} \Uplambda^{2} /2{\kern 1pt} \pi {\kern 1pt} \lambda$ [23] with λ of the free-space wavelength for the readout pulse.

Fig. 1

The configuration for studying the diffraction of femtosecond pulse from volume holographic grating (VHG). Two cw beams write a VHG and a femtosecond pulse incidents to readout

The broadband femtosecond readout pulse E _r with a central angular frequency ω ₀ (corresponding central wavelength λ ₀) enters the material at an angle of θ_r (the angle inside the material is θ_r’) and is diffracted by the refractive index grating. Here we assume that θ_r equals to the Bragg angle for the central wavelength λ ₀. In the following analysis, it is supposed that the readout femtosecond pulse has a Gaussian shape in time; the temporal amplitude of the readout pulse can be generally expressed as

$$ e_{\text{r}} (t) = \exp ( - i\omega_{0} t - t^{2} /T^{2} ) $$

(1)

where $\omega_{0} = 2\pi c/\lambda_{0}$ is the central frequency and c is the speed of light in free-space. The parameter T is related to the ΔT, a full width at half maximum (FWHM), by the following relation: $T = {{\Updelta \tau } \mathord{\left/ {\vphantom {{\Updelta \tau } {2\sqrt {\ln 2} }}} \right. \kern-0pt} {2\sqrt {\ln 2} }}.$

By applying Fourier transform on Eq. (1), the field distribution in the spectrum domain can be obtained:

$$ E_{\text{r}} (\omega ) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {e_{\text{r}} (t)} \exp (i\omega t)dt = \frac{T}{2\sqrt \pi }\exp [ - \frac{{T^{2} (\omega - \omega_{0} )^{2} }}{4}] $$

(2)

To describe the propagation and coupling between the transmitted and diffracted pulses in the VHG, the slowly varying field approximation is employed, after neglecting the quadratic and high order terms in the index change, we can obtain the modified Kogelnik coupled-wave equations,

$$ \begin{gathered} \frac{{{\text{d}}E_{t} (z,\omega )}}{{{\text{d}}z}} = - i\nu E_{d} (z,\omega )\sqrt {{{C_{S} } \mathord{\left/ {\vphantom {{C_{S} } {C_{R} }}} \right. \kern-0pt} {C_{R} }}} \hfill \\ \frac{{{\text{d}}E_{d} (z,\omega )}}{{{\text{d}}z}} + 2i\xi E_{d} (z,\omega ) = - i\nu E_{t} (z,\omega )\sqrt {{{C_{R} } \mathord{\left/ {\vphantom {{C_{R} } {C_{S} }}} \right. \kern-0pt} {C_{S} }}} \hfill \\ \end{gathered} $$

(3)

where $E_{t} \left( {z,\omega } \right)$ and $E_{d} \left( {z,\omega } \right)$ are the electric fields of the transmitted and diffracted beams, which are dependent on propagation distance z and angular frequency ω; in unslanted grating, $C_{R} {\kern 1pt} = C_{S} = \cos \theta^{\prime}_{\text{r}} ;\nu = \frac{\omega \Updelta n}{{2c\cos \theta^{\prime}_{\text{r}} }}$ is the coupling coefficient. For the broadband readout beam, it is impossible that all frequency components are met the Bragg condition, simultaneously in the VHG, so off-Bragg parameter $\xi = \frac{{i\pi^{2} c}}{{\Uplambda^{2} n_{0} \cos \theta^{\prime}_{\text{r}} }}\left( {\frac{1}{\omega } - \frac{1}{{\omega_{0} }}} \right)$ is introduced to represent the deviation from the Bragg condition. When the frequency of the readout spectral component satisfies the Bragg condition in the VHG, ω = ω ₀, ξ approaches zero.

Equation (3) is applicable to all frequency components within the spectrum of the readout femtosecond pulse. Substituting the initial conditions $E_{\text{t}} (0,\omega ) = E_{\text{r}} (\omega )$ and $E_{d} (0,\omega ) = {\kern 1pt} 0$ into the modified coupled-wave Eq. (3), the analytical solution for the diffracted field at the output plane is given by

$$ E_{d} (\omega ,\,d) = - i\nu {d} \cdot \exp (\xi \,d) \cdot \frac{{\sin \sqrt {(\nu d\,)^{2} - (\xi \,d)^{2} } }}{{\sqrt {(\nu d)\,^{2} - (\xi \,d)^{2} } }} \cdot E_{\text{r}} (\omega ) $$

(4)

The spectrum intensity of diffracted beam at the output plane is

$$ I_{d} (\omega ,d) = (\nu d)^{2} \frac{{\sin^{2} \sqrt {(\nu d)^{2} - (\xi d)^{2} } }}{{(\nu d)^{2} - (\xi d)^{2} }} \cdot E_{\text{r}}^{2} (\omega ) $$

(5)

According to the principle of reverse-Fourier-transform, the time variation of the diffracted field at the output plane is given by

$$ E_{d} (d,t) = \int\limits_{ - \infty }^{\infty } {E_{d} (\omega ,d)\exp ( - i\omega t)d\omega } $$

(6)

Then the time variation of the diffracted intensity is given by

$$ I_{d} (d,t) = \left| {E_{d} (d,t)} \right|^{2} $$

(7)

The spectrum distributions and the time variation of the diffracted beam are strongly dependent on the grating’s period, thickness, refractive index modulation and the duration of the input femtosecond pulse. The influences of these parameters on the diffraction are discussed in former literatures [24–26]. Here we focus on the effect of refractive index modulation of the VHG on the time variation of the diffracted intensity.

3 Numerical simulations of diffracted double pulses

In this section, the time variations of the diffracted intensity are investigated. During the simulation, we choose the FWHM of the readout pulse as $\Updelta \tau$ = 100 fs, central wavelength $\lambda_{0}$ = 1.5 µm (corresponding to central angular frequency $\omega_{0} = 4\pi \times 10^{14} {\text{rad/s}}$), background refractive index $n_{0} = 3.314$, grating thickness d = 7.5 mm, grating period $\Uplambda$ = 7.3 µm, light speed in free-space c = 3 × 10⁸ m/s and $\cos \theta^{\prime}_{r} = \sqrt {1 - \left( {{{\lambda_{0} } \mathord{\left/ {\vphantom {{\lambda_{0} } {2\Uplambda n_{0} }}} \right. \kern-0pt} {2\Uplambda n_{0} }}} \right)}$, after substituting these values into Eqs. (4–7), the time variation of diffracted intensity distributions with respect to the different refractive index modulations is numerically simulated. Here we focus on the emergence of diffracted double pulses as the refractive index modulation changes.

Figure 2 is the diagram of the time variations of diffracted intensity distributions when the refractive index modulations of the VHG change in the range of 1.0 × 10⁻³ to 5.50 × 10⁻³. It is obvious that double pulses have been generated. To a specific refractive index modulation, we can obtain two diffracted pulses with the same peak intensity and duration. As the refractive index modulation varies, the duration and peak intensity changes accordingly. Defining the pulse interval as the separation of two peaks of the diffracted double pulses, it is seen that as the refractive index modulation increases, pulse interval broadens, diffracted peak intensity and duration of the two pulses increases accordingly. Moreover, by defining the center of readout Gaussian pulse as t = 0, it can be seen that the symmetric centers of all diffracted double pulses shift to the negative time-delay and the displacements show the similar trend when the refractive index modulation varies.

Fig. 2

Time variations of diffracted double pulse when the refractive index modulations are Δn = 1.0 × 10⁻³, 1.50 × 10⁻³, 2.50 × 10⁻³, 3.50 × 10⁻³, 4.50 × 10⁻³ and 5.50 × 10⁻³, respectively

By increasing the refractive index modulations further from 5.50 × 10⁻³ to 6.50 × 10⁻³, the time variations of diffracted intensity distributions are shown in Fig. 3. It can be seen that all diffracted pulses include double pulses, and the pulse interval increases with the refractive index modulation. However, different from those diffracted pulses shown in Fig. 2, it is seen from Fig. 3 that all diffracted double pulses have similar pulse duration and peak intensity. In addition, the symmetric centers of all diffracted double pulses shift to the negative time-delay too, and the displacement has the similar trend as that in Fig. 2.

Fig. 3

Time variations of diffracted double pulses when the refractive index modulations are Δn = 5.50 × 10⁻³, 5.70 × 10⁻³, 5.90 × 10⁻³, 6.10 × 10⁻³, 6.30 × 10⁻³ and 6.50 × 10⁻³

When the refractive index modulations of the VHG are increased from 6.5 × 10⁻³ to 3.05 × 10⁻² with step of 0.6 × 10⁻³, the time variations of diffracted double pulses are shown in Fig. 4. It is interesting to note that all the diffracted pulses are double pulses and all the pulses have the same durations and peak intensities. The FWHM of each pulse is 70 fs. Evolution of the two-pulse interval with respect to the refractive index modulation shows the similar trend as those in Figs. 2 and 3, which means that with increasing the refractive index modulation of the VHG, the two-pulse interval increases. This fact suggests the possibility of generating interval adjustable double pulses by changing refractive index modulation. Moreover, the symmetric centers of diffracted double pulses have a negative time-delay shift.

Fig. 4

Time variation of diffracted double pulses when the refractive index modulations change from 6.50 × 10⁻³ to 3.05 × 10⁻²

4 Explanation on the emergence of diffracted double pulses

The intrinsic reason for emergence of the diffracted double pulses is due to the Bragg selectivity of VHG. When the refractive index modulations of the VHG change, some spectral components are filtered out and the diffracted spectral components synthesize into double pulses. The periodic evolvement of diffracted double pulse can be explained by the overmodulation effect of refractive index modulation [27, 31]. It can be seen from Eq. (6) that the time variation of the diffracted field E_d(d, t) can be regarded as a superposition of a series of monochromatic diffracted field with different frequencies and weights. From Eq. (4), we know the weight E_d(d, ω) is modulated by sine function, so does the time variation of the diffracted field. Therefore, the time variation of the diffracted intensity is modulated by the power of the sine function.

From Eq. (5), we know the diffracted intensity spectrum is governed by the term $\sin^{2} \sqrt {(\nu d)^{2} - (\xi d)^{2} }$. Since term $\sin^{2} \sqrt {(\nu d)^{2} - (\xi d)^{2} }$ is a periodic function of ν, the time variation of the diffracted intensity distribution is also a periodic function of ν. That is the reason the double pulses at different refractive index modulations are obtained in the previous simulation.

In $\sin^{2} \sqrt {(\nu d)^{2} - (\xi d)^{2} } ,\,\nu{d} = \frac{\omega \,\Updelta nd}{{2c\cos \theta^{\prime}_{r} }}$ is a function of Δn, while ξ is not, so the period of the emergence of diffracted double pulse is determined by νd with the periodicity of

$$ \nu{d} = \pi $$

(8)

According to the definition of $\nu = \frac{\omega \Updelta n}{{2c\cos \theta^{\prime}_{\text{r}} }}$, the period of refractive index modulation at which there exists diffracted double pulses is

$$ \Updelta (\Updelta n) \cdot d = \pi \cdot 2c\cos \theta^{\prime}_{\text{r}} /\omega $$

(9)

where Δ(Δn) represents the period of refractive index modulation to generate diffracted double pulses.

Substituting these values defined in Sect. 3 into Eq. (9), the period of refractive index modulation can be calculated to be Δ(Δn) = 2.0 × 10⁻⁴. In simulated data shown in Figs. 2, 3 and 4, we chose the refractive index modulations as integral times of the period of Δ(Δn), that is why diffracted double pulses are obtained.

$\nu{d} = \frac{\omega \,\Updelta nd}{{2c\cos \theta^{\prime}_{\text{r}} }}$ is also a function of grating thickness d. If the refractive index modulation is fixed, while the thickness of the VHG changes, the emergence of diffracted double pulses depends upon the period of thickness based on Eq. (8),

$$ \Updelta n \cdot (\Updelta d) = \pi \cdot 2c\cos \theta^{\prime}_{\text{r}} /\omega . $$

(10)

where Δd is the period of VHG thickness in which diffracted double pulses occur.

Fixing the refractive index modulation on $\Updelta n = 3 \times 10^{ - 3}$, Fig. 5 shows the time variation of the diffracted intensity distribution when the grating thicknesses are integral times of period of thickness, i.e., $d = 0.5,\;1,\;1.5,\;2,\;2.5$ mm. From Fig. 5, it can be seen that all the diffracted pulses are double pulses. Also, the diffracted peak intensity and pulse interval increase with the increasing grating thickness.

Fig. 5

Time variations of diffracted double pulses when the grating thickness changes from 0.5 to 2.5 mm

From former discussions, we know that as long as the relation between the thickness and refractive index modulation satisfies

$$ \Updelta n \cdot d = \pi \cdot 2c\cos \theta^{\prime}_{\text{r}} /\omega $$

(11)

the diffracted double pulses will appear periodically. As ν is irrelevant to grating period and duration of readout pulse, no matter how large these two parameters get, diffracted double pulses will never appear. It proves that the periodic emergence of the diffracted double pulses is due to the overmodulation effect of refractive index modulation and grating thickness. The diffracted double pulses are also emerged in Yi’s paper [28].

5 Relation between the pulse interval and refractive index modulation

According to the former discussions, the diffracted double pulses only occur at those refractive index modulations that are equal to the integral times of the period Δ(Δn) = 2.0 × 10⁻⁴. Choosing the refractive index modulations in the range of 1.0 × 10⁻³ to 3.05 × 10⁻² with the step of 2.0 × 10⁻⁴, Fig. 6 shows the relation between the refractive index modulation and pulse interval. The relation can be divided into two parts. The first part is within 1.0 × 10⁻³ to 4.5 × 10⁻³, as shown in the inner diagram of Fig. 6, where the relation between the refractive index modulation and pulse interval is nonlinear, the pulse interval increases slowly with the increasing of the refractive index modulations. When the refractive index modulation is greater than 4.5 × 10⁻³, the pulse interval is linearly proportional to the refractive index modulation, and the slope of linearity is determined to be 26.7 ps. This linear relation provides us with a convenient method to choose appropriate refractive index modulation to generate double pulses with a desired pulse interval.

Fig. 6

Relation between the pulse interval and refractive index modulations. The refractive index modulations are in the range of 1.0 × 10⁻³ to 3.05 × 10⁻²

6 Conclusion

Based on the Kogelnik’s coupled-wave theory and Fourier transformation, doubling of the incident femtosecond pulse is realized by adjusting the refractive index modulation of the volume holographic grating. It can be found when the index modulation changes in the range of 1.0 × 10⁻³ to 3.05 × 10⁻², we can get diffracted double pulses. However, when the refractive index modulations are in the range of 1.0 × 10⁻³ to 5.50 × 10⁻³, the peak intensity of diffracted double pulses is different. While the refractive index modulations are in the range of 5.5 × 10⁻³ to 3.05 × 10⁻², peak intensity of all diffracted double pulses is equal. When the refractive index modulation is larger than 4.50 × 10⁻³, the pulse interval is linearly proportional to the index modulations. This periodic emergence of double pulses can be explained by overmodulation of refractive index modulation of transmitted VHG. Comparing to alternative methods for generation of double pulses, our scheme needs only one volume holographic grating, the system structure is very simplified. Corresponding volume holographic grating can be made in BB-640 emulsions [27], photorefractive polymers [29], photopolymers based on PMMA [30] or PVA/acrylamide [31] and liquid crystal molecule [32], femtosecond laser induction [33] or photo-thermal-refractive glass [34].