1 Introduction

Transient absorption spectroscopy is a major tool for the study of the mechanisms of photochemical reactions. Since a photoreaction is initiated by absorption of light, a short light pulse can be used to synchronize the reactions in an ensemble of molecules. Subsequently, the optical absorption of the sample is measured as a function of the time delay t after the excitation pulse and as a function of the wavelength λ of the probe light. The result is a two-dimensional data array A(t, λ) which contains information on the spectra of the various intermediates involved in the photoreaction, and their kinetics. In most cases the sample before initiating the photoreaction is used as the reference, and the data correspond to the difference absorption \(\Updelta A(t,\lambda) = A(t,\lambda) - A(-\infty,\lambda). \) The method was introduced under the name flash photolysis by Norrish and Porter as early as 1949 [1], who received the Nobel price for this discovery in 1967 [2]. Whereas the original experiments had a time resolution in the millisecond range, the technique soon was extended to the microsecond and nanosecond time range. Under the name of pump-probe spectroscopy it is now used with femtosecond time resolution. Recent reviews can be found in references [3–5].

The highest time resolution can be achieved with ultrashort probe pulses, and the highest wavelength resolution is then obtained with transform limited pulses. Measurements with transform limited probe pulses require one excitation of the sample for each time delay t i and wavelength λ j . When M measurements are averaged for each data point, the sample has to be excited \(N_{\mathrm{ex}} = M \times N_{\hbox{T}} \times N_{\hbox{S}}\) times, where N T is the number of time points and N S is the number of spectral points in the data array. The data array is usually analyzed in terms of the kinetics of several species, often by application of multi-exponential fits. A reasonable fit requires a good signal to noise in the data which requires in turn the accumulation of typically M ≈ 100 measurements for each data point. Hence, filling a data array with N T = 500 time steps and N S = 500 spectral elements requires \(N_{\mathrm{ex}} = 2.5 \times 10^7\) excitations of the sample with intense laser pulses.

If the excited molecules undergo a photocycle with very high yield of recovery, such large numbers of excitations can be applied. However, typical organic photochromic molecules sustain only ≈1,000 pump probe pulse sequences, and in many cases the photoreaction is irreversible. Then the sample must be replaced by a fresh sample after every excitation, i.e., the available amount of sample limits the number of measurements that can be performed. In such cases it is advantageous to have a method that measures several data points in the data array following a single excitation of the sample. One option is to use monochromatic probe light of long duration and measure the transmitted light intensity as a function of time. In this case the time resolution is given by that of the detector, which is usually a photomultiplier. Each measurement yields a column of the data array, and the number of excitations required to fill the data matrix is \(N_{\mathrm{ex}} = M \times N_{\hbox{S}}. \) Alternatively, the data array can be measured one row at a time using a broadband short light pulse as a probe in combination with a spectrograph and a detector array, which requires \(N_{\mathrm{ex}} = M \times N_{\hbox{T}}\) excitations of the sample.

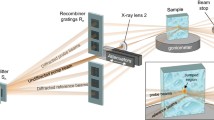
The ultimate efficiency with respect to the actinic stress applied to the sample is obtained if a broadband (white) light pulse of long duration is passed through the sample and is subsequently analyzed both with respect to time and wavelength. This can be achieved by the combination of a spectrograph and a streak camera. Streak cameras have been developed as time analyzers for light pulses with a time resolution of a few ps. Their function is schematically shown in Fig. 1. The light pulse to be analyzed is directed onto a photocathode K where photoelectrons are ejected. These are accelerated towards a detector consisting of a multichannel plate and a phosphor screen. A voltage ramp applied along the x-direction deflects the electrons so that photoelectrons generated at later times hit the detector at increasing values of x. In this way the temporal structure of the light pulse is transformed into a spatial image on the phosphor screen. This image is recorded by a CCD camera, digitized, and processed by a computer. If the photocathode extends into the y-direction perpendicular to x and z, many light pulses applied along the y-direction are analyzed simultaneously. In our setup these light pulses correspond to different wavelengths, produced by spectral dispersion of the input light pulse along the y-direction by a spectrograph.

Fig. 1
figure 1

Principle of a streak camera

Full size image

Among the first applications of streak cameras was the diagnostics of ultrashort laser pulses and other light emission events of short duration. If the light to be analyzed is first dispersed in one direction by a spectrograph and subsequently dispersed temporally in the orthogonal direction by the streak camera, an image of the spectro-temporal characteristics can be recorded for a single light event (e.g. from an explosion). The first report of the use of a streak camera for transient absorption measurements that we could find in the literature is a communication by Müller from 1976 [6]. He reports on the transient absorption spectra of dyes. A Xe flashlamp of 5 μs duration was used as the probe light, and the streak image was recorded by a photographic plate and analyzed by a computer controlled microdensitometer. Peak positions assigned to S\(_1 \rightarrow\) S n transitions are given, but no time information, and no original data are shown. Three years later Yoshihara et al. [7] reported time profiles from the transient absorption of trans stilbene with a time-resolution of ca.10 ps. The fluorescence of a dye was used as probe light. Other groups reported similar setups in the 1980s [8–11]. The first report of a measurement using wavelength dispersion in combination with time dispersion is by Ito et al. in 1991 [12]. However, only data that were averaged over all wavelengths or over a certain time interval are discussed. This is also true for several later papers from the same group [13–17]. Whereas most of the papers mentioned before report a streak camera measurement mostly as a proof of principle, the groups of Kelley [18–20] and Du-Jeon Jang [21–28] apparently used their setup for further studies. In all of these studies, the signal to noise ratio is in the range S/N ≈ 3–5, or the standard deviation in the transient absorption is in the order of 0.3 optical density units. Hence only monoexponential decays of a single species can be analyzed. The main source of fluctuations in these experiments is the low reproducibility of the temporal profile of the probe light, which is either fluorescence from a dye or the emission of a plasma produced by focussing a strong laser pulse into compressed Xe gas. Another limiting factor is the low dynamic range of ca. 100:1 of the streak camera.

Our project follows a quite different approach. In the past decades, powerful pump-probe methods have been developed for the study of transient absorption in the time range of a few fs up to 10 ns. If sufficient sample is available for the large number of pump probe pulse sequences required, these methods are far superior to a streak camera measurement. Our interest is in transient absorption measurements in the time range of 10 ns up to 10 ms on molecular systems which are available only in small quantities and cannot sustain many pump probe pulse sequences. Of particular interest are photoactive proteins related to light sensing functions in plants and algae which undergo the photoreaction only once or need hours to recover from a photoexcitation. Our aim is to extract a maximum of information on the spectral and temporal dynamics for each excitation of the sample. In contrast to all previous studies on transient absorption with streak cameras we use a streak camera with particularly large dynamic range of ca. 104. For the probe light we use a pulsed Xe lamp which provides a flat time profile over a time period of several ms with fluctuations less than 0.1 %. As far as we know, our setup is the first that analyzes the complete two-dimensional data array in terms of multimodal kinetics of several species. Two applications of the setup to the study of a light sensing protein [29] and a photocatalytic reaction [30] have already been published. Here we give a detailed account of the design and the performance of the apparatus.

2 Experimental setup

The setup is schematically shown in Fig. 2. The sample is excited by a light pulse which is generated either directly by a Nd:YAG laser (532 or 355 nm) or by an optical parametric oscillator (OPO) pumped by the third harmonic of the Nd:YAG (Surelite II and Surelite OPO PLUS, Continuum). The pulse duration is typically 8 ns, and the energy typically 10 mJ. For stable operation the laser runs with a constant repetition rate of 10 Hz and a single pulse is selected with a high-energy shutter (LS055, nmLaser). The probe light is generated by a pulsed xenon flash lamp (MSP-05, Müller Elektronik–Optik) which produces a white light pulse with very flat intensity profile of adjustable duration (250 μs–10 ms). In order to make the light path achromatic, the probe light is focused three times by toroidal mirrors (aluminium-coated blanks of eyeglass lenses, Rodenstock): At the first focus a shutter (LS6ZM, Uniblitz) is placed which blocks access of the continuous background light of the pulsed xenon light source to the sample. The second focus is placed at the sample position, the third on the entrance slit of the spectrograph (Bruker 200is) equipped with a grating having 100 lines / mm. After spectral dispersion by the spectrograph the light is temporally analyzed by the streak camera (C7700, Hamamatsu Photonics). The latter consists of two parts: the streak tube which produces an image on a phosphor screen, and a CCD camera (ORCA-CR, Hamamatsu Photonics) which digitizes this image. The streak camera is operated in the single shot and gate modes at the smallest possible gain to collect as many photons of the probe light as possible. Temporal control of all components is achieved with home-built electronics. Samples with very long recovery time are studied in a fused silica flow cuvette (Starna) attached to a peristaltic pump (LKB-pump P-1, Pharmacia).

Fig. 2
figure 2

Schematic of the setup

Full size image

A transient absorption measurement requires four streak images:

$$ \Updelta A = -\log \left( \frac{I_{\hbox{LP}}-I_{\hbox{L}}}{I_{\hbox{P}}-I_{\hbox{D}}} \right) $$
(1)

In this expression I LP is the intensity image obtained when both laser and probe light are on, I L and I P are the intensities when only the laser or the probe are on, respectively, and I D is the dark image. The measurements of these four images is performed in the sequence ILP, ID, IL, IP. This sequence is repeated M times. When only small amounts of sample are available, i.e., when consecutive measurements have to be performed with the same sample, the cycle time t C between two consecutive ILP measurements must be comparable to the recovery time of the photochemical reaction. For some biological photosensor proteins like LOV domains (see below) t C can be several minutes. It is then important that the measurement of IL occurs at t C/2 so that the sample can recover for the same time after each laser excitation.

When the fluorescence generated by the sample is very intense, subtraction of an image with the laser alone may not result in complete cancelation. In this case we found it easier to omit the measurement of IL and replace I L with I D in the numerator of Eq. 1. The fluorescence then appears as an apparent negative transient absorption which can in many cases be well fitted by the instrument response function. As a benefit, the fluorescence spectrum is obtained within the TA measurement. This should be compared with the situation of one-dimensional TA measurements at fixed wavelengths, which are usually performed with a photomultiplier having an active voltage divider (i.e., one with transistors instead of resistors). When such a multiplier is hit by strong fluorescence, it becomes “blind” for several milliseconds. Thus, in our earlier (one-dimensional) measurements of TA in flavin-containing protein domains [31–33], measurements were not possible in the spectral region of the fluorescence. As will be shown below, this is no longer the case with the streak camera.

The amount of probe light injected into the sample was measured with the well-known ferrioxalate actinometer [34]. A 0.15-M solution of Fe(III) oxalate in water was excited in the same cell and with the same optical arrangements as in the transient absorption experiments. The flash pulse was set to the highest intensity with a pulse duration of 250 μs. This intensity is sufficient for a measurement in the 10-μs time window of the streak camera. For larger time windows the intensity could be reduced accordingly. The actinometer solution captures all photons in the range 315–470 nm, given by the cutoff filter (Schott WG 305) and the absorption band of the Fe(III) oxalate. Under these conditions we find that 9.3 × 1014 photons are absorbed. Less than 5 % of these photons are needed in the 10-μs time window, but with the standard electronics of the flash lamp we cannot make the pulse duration shorter than 250 μs. If damage to the sample by the probe light should become a problem, faster switching of the probe light pulse could solve this. We used the photocatalytic oxidation of methyl benzylalcohol (MBA) with riboflavin tetraacetate (RFTA) to measure the stress applied to the sample by the pump laser. The sample contained MBA and RFTA in concentrations of 30 mM and 40 μM, respectively, resulting in an optical density of 0.5 along a 1-cm path. The photochemical turnover in this sample was 0.43 μM/pulse for the pump laser and 0.45 μM/pulse for the 250 μs probe flash pulse. Thus the stress applied by the pump and the probe pulse are of similar magnitude, but the latter could be reduced considerably be reducing the probe pulse duration.

3 Data analysis

The data sets produced by the streak camera are transient absorption differences as functions of time and wavelength, \(\Updelta A(t,\lambda). \) For a set of discrete N T time points t i and N S wavelengths λ j these data form a rectangular matrix \({\boldsymbol\Updelta {\user2{A}}}\) of dimension N T × N S with matrix elements \(\Updelta A_{ij} = \Updelta A(t_i,\lambda_j). \) Every column of the matrix is a time-trace for a fixed wavelength; every row is a spectrum at a given delay time. Many techniques have been developed for the analysis of data matrices of this kind, and recent reviews can be found in [35–38]. In the following we give a short account of those techniques that we usually apply.

We wish to decompose the data matrix into sum of products of one-dimensional functions:

$$ \Updelta A_{ij} = \sum_{k=1}^N c_k(t_i) S_k(\lambda_j) = \sum_{k=1}^N c_{ik} S_{kj} $$
(2)

Such a decomposition can in principle be done exactly, and in an infinite number of ways, when N is equal to the full rank of the data matrix, \(N = {\mathrm{Min}}(N_{\hbox{T}},N_{\hbox{S}}). \) One particularly useful technique is singular value decomposition (SVD). However, we are interested in a decomposition with only a small number of components N C ≪ N corresponding to the number of spectrally distinct chemical species involved in the photoprocess. The k-th column of the matrix c then contains the concentration time profile of species k, whereas the k-th row of the matrix S contains the spectrum of species k. Obviously, truncation of the sum in Eq. 2 results in a model data matrix D which only approximately reconstructs the original data \({\boldsymbol\Updelta {\user2 A}}. \)

$$ D_{ij} = \sum_{k=1}^{N_{\hbox{C}}} c_{ik} S_{kj} $$
(3)

Finding the “best” solution constitutes an optimization problem that can, e.g., be solved by minimizing the sum of squares

$$ \chi^2 = \parallel {\boldsymbol\Updelta {\user2 A}} - {\user2 D} \parallel^2 = \mathrm{Min} $$
(4)

Ideally one would do the decomposition with no or only a small number of assumptions. We do the analysis in several steps. The first step is model independent and extracts the significant information from the data. The effective rank of the matrix is determined by SVD, setting an upper limit to the number N C of distinguishable species involved. Further processing can then be done either with the original data set or with a reduced data set truncated to the first N C most important components with the largest singular values. One option is solving Eq. 4 with a global fit, employing a suitable model either for the concentration time profiles or the spectra. The other option is performing an inverse Laplace transform along the time axis, leading to a spectral distribution of rate constants p(k, λ). Sometimes the data matrix contains invalid data, e.g. strong scattered laser light, or strong fluorescence that cannot be canceled to a degree required for the application of the fit or the Laplace transform. In these cases the part of the matrix containing invalid data must be modified in an appropriate way.

In the following sections we shall first describe the SVD and rank analysis, followed by a short outline of the fit procedure. The procedure developed by us for correction for scattered laser light and/or fluorescence is described next. Although it would appear logical to describe this before the fit, we use the reversed order here since the technique is integrated into the fit procedure. The last section discusses the shortcomings inherently present in a multiexponential fit and describes the method used for the inverse Laplace transform. The latter is based on a maximum entropy concept.

3.1 SVD and rank analysis

Singular value decomposition (SVD) decomposes a matrix \({\boldsymbol\Updelta {\user2 A}}\) with N r rows and N c columns into the product of three matrices U, W, and V as

$$ {\boldsymbol\Updelta {\user2 A}} = {\user2 U W V}^t $$
(5)

where the superscript t represents the transposed matrix. We assume that N r ≥ N c; otherwise the decomposition is done with the transposed matrix \({\boldsymbol\Updelta {\user2 A}}^t. \) The matrix U has the same dimension as \({\boldsymbol\Updelta {\user2 A}}, \) and the columns of U are mutually orthogonal. W and V are square matrices of dimension N c. V is an orthogonal matrix, and W is diagonal with diagonal elements w j  ≥ 0 usually ordered in descending order. The reconstruction of the matrix \({\boldsymbol\Updelta {\user2 A}}\) with the first K components is then the best representation of the original matrix by a sum of K bilinear products:

$$ {\boldsymbol\Updelta {\user2 A}}^{(K)} = \sum_{k=1}^K {\user2 u}(k) w_k {\user2 v}^t(k) $$
(6)

In this expression u(k) refers to the k-th column of the matrix U. Thus the standard deviation σ(K) defined as

$$ \sigma^{(K)} = \sqrt{\left| \left| {\boldsymbol\Updelta {\user2 A}}^{(K)} - {\boldsymbol\Updelta {\user2 A}} \right| \right|^2} $$
(7)

is the smallest standard deviation that can be expected for a fit to \({\boldsymbol\Updelta {\user2 A}}\) by a model of the form of Eq. 3 with K components. A plot of σ(K) versus K yields a monotonously decaying curve. Usually, this curve shows a steep slope for small values of K, until σ(K) comes close to the experimental noise level. The first component that does not lead to a significant improvement of σ(K), as well as all further components, can then be regarded as representing noise. Truncation of the reconstruction of Eq. 6 to only the significant components yields a data matrix which has been effectively filtered for noise. For example, reconstruction of a 512 × 512 matrix to 4 components is equivalent to averaging over 128 columns and 128 rows, but without any loss in temporal or spectral resolution. Representing the data as a 3D surface plot usually requires such a filtering. An example of this procedure is presented in the performance section.

3.2 Global lifetime analysis

The global lifetime analysis assumes that the data can be modeled by a factorization into a sum of products of spectra S k (λ) and concentration time profiles c k (t) as defined in Eq. 2, where the time profiles can be written as a linear combination of known analytic functions f j (t), 

$$ D_{ij} = \sum_{k=1}^{N_{\hbox{C}}} c_k(t_i) S_k(\lambda_j) $$
(8)
$$ c_k(t) = \sum_{l=1}^{N_{\hbox{F}}} f_l(t) X_{lk} $$
(9)

Here, N C is the number of distinct spectral species, and N F the number of analytic time functions. Defining C as a N T × N C matrix with elements C ik  = c k (t i ), and F as a N T × N F matrix with matrix elements F il  = f l (t i ), the model data matrix D can be written in the following form:

$$ {\user2 D} = {\user2 C S} = {\user2 F X S} = {\user2 F B} $$
(10)

The k-th row of the matrix B with elements B kj  = b k (λ j ) corresponds to the spectral changes associated with the time function f k (t). When these time functions are exponential decays (convoluted with the instrument response), the corresponding spectra are called decay-associated difference spectra (DADS). Optimization corresponds to solving the least squares optimization problem

$$ \chi^2 = \parallel {\boldsymbol\Updelta {\user2 A}} - {\user2 F B} \parallel^2 = \mathrm{Min} $$
(11)

Efficient algorithms exist that solve Eq. 11 for fixed matrices \({\boldsymbol\Updelta {\user2 A}}\) and F. The value of χ2 optimized in this way is further minimized by a nonlinear least squares algorithm by variation of the rate constants in F. The DADS and the corresponding rate constants are the unique result of this global lifetime analysis. This treatment does not require any model for the kinetics involved in the transient processes. The details of such a model will be entirely defined in the matrix X that relates the actual species kinetics to the elementary function f k (t). Once a model and thus the appropriate matrix X has been chosen, the species-associated difference spectra in matrix S can be calculated by

$$ {\user2 S} = {\user2 X}^{-1} {\user2 B} $$
(12)

3.3 Eliminating invalid data

Efficient algorithms exist that solve the linear least squares problem of Eq. 11. These require the full rectangular data matrix \({\boldsymbol\Updelta {\user2 A}} \),or a SVD decomposition of it. Scattered laser light or a strong fluorescence signal will, however, make small spots on the data image invalid for this analysis. Hence these data must be excluded. Since the matrix may not have “holes”, this means that the invalid data must be replaced with something else. We tested two strategies.

In the first strategy, the invalid data area is “patched” by replacing all data points in a certain area by values obtained by interpolation of the values along the border of that region. The second strategy replaces the invalid data by the values of the fit according to Eq. 11. This is done in every iteration. Upon convergence, these data hence do not contribute to the sum of squares. To the best of our knowledge this second technique seems to be new. When the second method is used, the patching will yield a global fit to the full data matrix as byproduct.

3.4 Maximum entropy analysis

A global fit with exponential functions yields a set of rate constants k j and the DADS P j (λ):

$$ A(t,\lambda) = \sum_{j=1}^N f(t,k_j) P_j(\lambda) $$
(13)
$$ f(t,k) = \int\limits_{-\infty}^t dt^\prime \exp (-k (t-t^\prime) ) g(t^\prime) $$
(14)

I.e., f j (t) is the exponential decay function with rate constant k j convoluted with the instrument response function g(t). The latter is approximated by a Gaussian centered at the peak of the excitation laser pulse. Multiexponential fits are notoriously ill-posed problems. As a result, small variations in the noise (e.g. from different measurements on the same system) can lead to substantial variations in the fitted parameters. This can be understood by considering the limit of infinite N. In this limit the set of rate constants becomes a distribution function p(k), i.e., the signal A(t) is the transform of p(k), as shown in Eq. 15 for a fixed wavelength.

$$ A(t) = \int\limits_{0}^\infty dk\,f(t,k) p(k) $$
(15)

In the limit that the apparatus function approaches the Dirac delta function, g(t) = δ(t), this is the Laplace transform. In the practical application we found it more convenient to use \(q = \ln k\) as the variable, i.e., defining

$$ A(t) = \int\limits_{0}^\infty dq\,R(t,q) p(q) $$
(16)
$$ R(t,q) = f(t, \exp(q)) $$
(17)

For the numerical implementation the variables t and q are taken as discrete values in equidistant steps, i.e., A i  = A(t i ), p j  = p(q j ), and R ij  = R(t i , q j ). The transformation is then accomplished by the matrix multiplication

$$ {\user2 A} = {\user2 R p} $$
(18)

An example is shown in Fig. 3. In the upper part, a double-exponential decay has been simulated. The ratio of the two rate constants is 1:3, with equal amplitudes. The lower part shows two distributions p(k) that fit the experimental data equally well. One corresponds to a double-exponential fit, i.e., it consists of two sharp spikes. The other shows two broad bands which indicates that quite some amount of uncertainty in the rate constants can be tolerated.

Fig. 3
figure 3

Top: a decay curve simulated as a sum of two exponential decays with equal amplitudes convoluted with a Gaussian instrument response function. The ratio of the rate constants is 1:3. Bottom: distribution of rate constants p(k) obtained by a double-exponential fit (full line) and by the maximum entropy method (dotted line). Both distributions yield the same quality of fit to the data set

Full size image

The dotted curve in Fig. 3 has been obtained with the maximum entropy method [39, 40]. This method optimizes the distribution function p(k) with respect to two criteria: First, the fit must be compatible with the data. This is maintained by fixing the average square deviation to the square of the standard deviation of the measurement.

$$ \chi^2 = \sum_j^{M_{\hbox{D}}} \left( \frac{A_j - A_j^{\hbox{exp}}}{\sigma_j}\right)^2 = M_{\hbox{D}} $$
(19)

In this expression, A exp j is an experimental data point, σ j the corresponding standard deviation, A j the calculated data point according to Eq. 15, and M D is the number of data points. The second constraint is that the distribution p(k) should not contain more information than required to fit the data. This is maintained by maximizing the configurational entropy S of the distribution.

$$ S = -\sum_{l=1}^{M_{\hbox{L}}}p_l \ln p_l $$
(20)

I.e., the distribution function p(k) is represented by M L discrete values p l  = p(k l ). In this way the maximum entropy method yields the distribution p(k) with the smallest information content [41]. In other words, every other distribution contains information for which no evidence exists in the data [40]. As far as we know, the first use of the maximum entropy method for solving the inverse Laplace problem with a positive amplitude distribution has been given by Livesey et al. [42]. Later, other empirical functions have been proposed as entropy functions that have no sign restriction on the distribution. A review and critical comparison can be found in [43]. We use a subroutine, kindly provided to us by Geoff Daniell [39] in 1995, for solving the maximum entropy problem with the definition of Eq. 20 since this has a strict justification by information theory.

Already, moderate amount of noise can significantly lower the true information content of a data set. This is exemplified in Fig. 4. In the upper panel the same double-exponential decay as in Fig. 3 is shown, with increasing amount of noise added. The corresponding maximum entropy distributions are shown in the lower panel. If the noise is larger than 1.6 % of the peak intensity, two decay rates which differ by a factor of three can apparently no longer be distinguished. Application of the maximum entropy technique to the analysis of streak camera images requires two modifications: these data contain decays with positive and negative amplitudes, whereas the entropy expression (Eq. 20) allows only for positive values. This can be accounted for by representing the distribution p as the difference between two distributions,

$$ {\user2 p} = {\user2 p}^+ - {\user2 p}^- $$
(21)

The transformation then takes the form

$$ {\user2 A} = \left( \begin{array}{ll} {\user2 R} , & - {\user2 R} \\ \end{array} \right)\left( \begin{array}{l} {\user2 p}^+ \\ {\user2 p}^- \\ \end{array} \right) $$
(22)

Every column r(q) of the matrix R contains the time profile expected for a species that decays with the corresponding rate constant \(k = \exp (q). \) The fastest rate constant is taken as the inverse of the time interval of one pixel of the streak image; the slowest rate constant is set to the inverse of ten times the total time window of the measurement. Between these two limits, 510 equidistant steps are taken on a logarithmic scale. An additional column of R is filled with the time profile corresponding to k = 0, and one column contains the constant value 1. The corresponding two values of the distribution p account for all decay processes that show no significant decay within the measurement time window and for a non-zero baseline of the whole image.

Fig. 4
figure 4

Top: simulated double-exponential decay, convoluted with a Gaussian apparatus function, and with increasing amount of Gaussian noise added. Bottom: distribution of rate constants p(k) obtained by the maximum entropy method for each of the decay curves of the upper panel. When the noise exceeds 1.6 % of the peak intensity, no evidence for two distinct rate constants is left in the data

Full size image

Since the numerical solution of Eq. 22 is rather time consuming, the algorithm has been implemented to solve for the first N C significant columns of the matrix U from the singular value decomposition of the matrix A instead of the whole matrix A, resulting in a distribution \(\hat{{\user2 p}}\) in the space of SVD components. The true distribution p is then obtained by SVD back transform.

$$ {\user2 U} = \left( \begin{array}{ll} {\user2 R} , & - {\user2 R} \\ \end{array} \right)\left( \begin{array}{l} \hat{{\user2 p}}^+ \\ \hat{{\user2 p}}^- \\ \end{array} \right) $$
(23)
$$ {\user2 p} = ( \hat{{\user2 p}}^+ - \hat{{\user2 p}}^-) {\user2 WV}^t $$
(24)

The trick of using Eq. 21 for dealing with negative amplitudes has been used by others before (e.g. [44, 45]).

We presently analyze the data from each time window separately. If two time constants differ by less than about a factor of 10, they can be detected within the same time window. If they differ by a much larger factor, they can be found by a separate analysis of two separate measurements in two different time windows. One might think of a more elaborate analysis by a simultaneous fit to data from different time windows. The data could be concatenated by taking from each larger time window the part that appends to the end of the previous window, after correction for the position of the excitation event. This procedure would at the same time give more weight to the data relating to the faster processes. Ideally, the time steps should increase in a logarithmic scale.

4 Performance

4.1 LOV-C57G

In the following the performance of the streak camera for TA measurements is shown with a mutated LOV-domain as an example. This protein domain is part of a blue-light photoreceptor in the green alga Chlamydomonas reinhardtii (C.r.). In this domain, the photoactive cysteine of the wild-type LOV is replaced by glycine. This introduces a shortcut into the photocycle which now proceeds from the triplet state of the flavin back to the ground state with a time constant of ca. 30 μs. Figure 5 shows false color representations of data sets obtained with increasing number of accumulated pump-probe pulse sequences M = 1, 10, and 100. The graph in the top of Fig. 5 shows the result of a measurement with only a single pump-probe pulse sequence. The fluorescence of flavin is clearly visible as the narrow blue horizontal stripe. With M = 10 (middle panel) the bleaching of the flavin ground state is clearly visible as a green vertical stripe centered at 450 nm. Red colored stripes on both sides indicate transient absorption by the triplet state. Accumulation of 100 pump-probe pulse sequences (bottom panel) results in a large improvement of the signal-to-noise ratio. However, the bleaching of the ground state can already be noticed in the picture for M = 1.

Fig. 5
figure 5

False color map of the 2D transient absorption matrix measured after photoexcitation of the LOV1-C57G domain of C.r. The three panels correspond to the accumulation of 1, 10, and 100 pump-probe pulse sequences from top to bottom. Yellow and red indicate positive signal which is assigned to the flavin triplet state absorption. Green and blue data regions correspond to bleaching of the flavin ground state and fluorescence

Full size image

A global lifetime analysis of these data sets reveals two lifetime components. One is short with fitted decay times between 40 and 60 ns. In the 20-μs time window, 40 ns correspond to a single pixel and hence the decay of this component is not resolved. The corresponding spectrum, shown in the upper part of Fig. 6, is negative throughout the whole wavelength range with peaks at 495 and 520 nm. It is assigned to the fluorescence. The second component is fitted by a monoexponential decay with a lifetime of 30 μs with M = 100. The lifetime is only slightly longer (33 μs) when only ten measurement cycles are averaged. The measurement with only a single pump-probe pulse sequence yields, however, a much larger lifetime. Interestingly, the corresponding spectra are very similar for all three measurements. Apparently, the spectral information is reliable already with M = 1, whereas the temporal information requires about M = 10. The transient amplitude of −20 mOD at the absorption maximum of the flavin chormophore near 445 nm indicates that ca. 5 % of the chromophores were bleached by the pump laser pulse.

Fig. 6
figure 6

Decay associated difference spectra of the fast and the slow component of a global fit to the data sets measured with N = 1 (black curves), N = 10 (red curves), and N = 100 (green curves). The fast component is assigned to fluorescence, and the fitted lifetimes (59, 51, and 40 ns for N = 1, 10, 100, respectively) correspond to the time resolution for this time window of the streak camera. The fitted lifetimes for the slow component, assigned to triplet-triplet absorption of flavin, are 80, 33, and 30 μs

Full size image

The effective rank of the data matrix can be found by inspection of the plot of the residual error σ(K) versus the number of components K as shown in the inset of Fig. 7. In case of the LOV1-C57G domain we find K = 2. Hence we may interpret σ(2) as the noise in the data sets shown in Fig. 7. A plot of σ(2) versus \(\sqrt{M}\) yields a perfect straight line, indicating that this noise scales with the square root of the number M of averaged pump-probe pulse sequences as expected for quantum noise. The average number of photons of the probe light that are accumulated on every pixel of the streak image is proportional to the product of M and the width of the time window. Hence a reliable measurement within the 2-μs time window should require either M = 10 accumulated pump-probe pulse sequences, or an increase of the intensity of the probe light by a factor of 10.

Fig. 7
figure 7

The first three temporal (panel a) and spectral (panel b) components u k and v k from SVD of the data set measured with accumulation of 10 pump-probe pulse sequences (panel (b) of Fig. 5). The plot of σ(K) versus K is shown as inset. The third component does apparently not improve the standard deviation, and the corresponding vectors u 3 and v 3 show only noise

Full size image

4.2 Acetabularia rhodopsin

This rhodopsin from the green alga Acetabularia acetabulum has first been identified by analysis of the genome and was subsequently expressed in Xenopus oocytes [46]. Electrophysiological experiments showed that it acts as a proton pump like bacteriorhodopsin. Of all proton pumping rhodopsins known so far, this Acerhodopsin shows the shortest wavelength absorption band with peak at 520 nm, shifted by 48 nm to the blue with respect to bacteriorhodopsin. Although Acerhodopsin has been known for several years, the photocycle could not be studied since only very small amounts could be produced. We received two samples, one from J. Tittor and one from Hegemann [46]. Measurements were performed with 300 μl solution with optical density of 0.3 over 1 cm path length at 520 nm. The data matrix obtained from this sample in the 20-μs time window and accumulated over 100 pump-probe pulse sequences is shown in Fig. 8. Acerhodopsin is a membrane protein. Hence, solutions show some degree of light scattering even when a detergent is used to force solubilization. The scattered laser light results in an intense signal on the streak image confined to a small spectral and temporal region, shown in the upper left magnified section in Fig. 8. Due to the high intensity the values are outside of the range of the false color scale and are hence shown as a white spot. When the iterative patching procedure outlined above is applied to the area marked by the dashed line, the result shown in the right magnified section is obtained. The data matrix was globally fitted with three exponential functions, and the values in the marked rectangle always adjusted to follow the fit. SVD of the original data matrix indicates the presence of three significant components (see black curve in Fig. 8d), whereas after the patching only two components remain. This might appear as a conflict with the requirement of three exponential functions for the fit. However, the DADS, shown in Fig. 9b as dots, reveal that two species have very similar spectra. Inspection of the data matrix shows a species with absorption near 600 nm immediately after excitation which decays on a time scale of 20 μs. The DADS with time constant of τ1 = 21 μs (black dots) shows a broad band for the decaying species, with peak at 580 nm that partly overlaps with the ground state absorption. This decay results in the production of a species with absorption maximum at 400 nm (negative peak in the DADS). This species decays with time constant τ2 = 224 μs into another intermediate with a broad absorption band that is very similar to that of the first intermediate (DADS with blue dots in Fig. 9b). This can also be seen directly in the data matrix of figure where the absorption at 600 nm first disappears and then reappears again. The third DADS, corresponding to infinite lifetime on the time scale of the experiment and shown as red dots in Fig. 9b, represents the difference spectrum of the third intermediate and the ground-state spectrum.

Fig. 8
figure 8

False color representation of the 2D transient absorption data measured for Acetabularia rhodopsin. The magnified sections show the region containing scattered laser light before and after application of the iterative patching method

Full size image
Fig. 9
figure 9

a 2D representation of the distribution of rate constants p(log k, λ) obtained by maximum entropy inverse Laplace transformation of the data matrix in Fig. 8. b Comparison of the DADS (dotted lines) from a biexponential fit and the spectra obtained by integration of p(log k, λ) over the rate constant intervals indicated. For discussion see text

Full size image

Instead of a global fit the data matrix can also be analyzed by the maximum entropy method. The resulting matrix of the distribution p(log k, λ) is shown in Fig. 9a. The false color plot reveals three regions along the log k axis where spectral changes occur: one near log k ≈ − 2.34, corresponding to lifetimes in the range τ = 220 ± 64 μs, a second region near log k ≈ − 1.28, corresponding to lifetimes in the range τ = 19 ± 8 μs, and a third region log k <  − 3, corresponding to lifetimes in the range τ > 1ms, i.e., outside of the time window covered by the experiment. Integration of p(log k, λ) over the corresponding ranges along the log k axis, as indicated by the dashed lines in Fig. 9a, results in the spectra shown as thin lines in Fig. 9b. Apparently, these are very similar to the DADS obtained by the global fit. The latter would correspond to a distribution p(log k, λ) that consists of three δ-functions along the log k axis. The maximum entropy method yields, in addition to the “peak”-lifetimes, also a measure of the uncertainty in these lifetimes. In the present case, the characteristic rate constants of the system differ by more than a factor of 10, and hence the peaks along the log k axis are well separated. Thus, the maximum entropy technique yields an a-posteriori justification for the use of a multiexponential fit in this case.

4.3 Study of a photocatalytic reaction

As third example we present a study on the mechanism of the photocatalytic oxidation of p-methoxy benzyl alcohol (MBA) with riboflavin tetraacetate (RFTA) as photocatalyst. A detailed analysis together with fs transient absorption measurements has been presented in Ref. [30]. Here we present a more recent data set for the ns–μs time range on the same system, measured with improved signal to noise ratio. The results of the previous report are confirmed, but more details became visible.

The data matrix shown as false color plot in panel (a) of Fig. 10 was obtained by accumulation of 100 pump-probe pulse sequences of 30 mM MBA and 40 μM RFTA dissolved in acetonitrile/water (50:50-v/v). The data matrix covers a time range of 20 μs and the spectral range of 335–755 nm. Red and yellow colors indicate absorption; green and blue colors correspond to bleaching. The white spots at t = 0 near 445 nm and in the range 490–610 nm indicate signals exceeding the color coding scale. They are caused by scattered light of the excitation laser and the flavin fluorescence, respectively. After “patching” the data matrix for the laser scatter and strong fluorescence, global lifetime analysis yields three components with lifetimes of 0.93, 6.0, and ≫ 20 μs. The three corresponding decay-associated difference spectra (DADS) are shown in panel (b) of Fig. 10 as the black, green, and red curves, respectively. They contain the spectral signatures of the flavin triplet state 3RFTA at 700 nm, the radical anion 2RFTA·− at 360 and 480 nm, and the protonated neutral radical 2RFTA-H· at 600 nm, as well as a negative band at 445 nm corresponding to bleaching of the RFTA ground state. The DADS are linear combinations of the species associated spectra (SAS), and the linear coefficients reflect the reaction mechanism. The best agreement with published spectra for the three flavin species is obtained with the mechanism depicted in Fig. 11: Following excitation to the excited singlet state, 1RFTA decays either by fluorescence to the ground state or by intersystem crossing to the triplet state 3RFTA. This process occurs within 3 ns and is not resolved in our measurement. A fraction of α = 25 % of the triplet state reacts with MBA and forms the radical anion 2RFTA·−, whereas the other 75 % decay back to the ground state. The sum of both decays results in a lifetime of 0.93 μs for the triplet state. A fraction of ca. 46 % of the radical anion falls back to the ground state, presumably via back electron transfer to MBA. The remaining fraction of ca. 54 % is protonated to yield the neutral radical 2RFTA-H·. Transformation of the DADS with this model yields the SAS shown in panel (c) of Fig. 10.

Fig. 10
figure 10

a False color representation of the 2D transient absorption data measured for a solution of riboflavin tetraacetate (40 μM) and p-methoxy benzylalcohol (30 mM) in acetonitrile/water (50:50-v/v). b DADS obtained by a global fit with three exponential functions. c Species-associated spectra obtained by transforming the DADS according to the mechanism depicted in Fig. 11

Full size image
Fig. 11
figure 11

Mechanism proposed for the initial steps of the flavin based photocatalytic oxidation of p-methoxy benzyl alcohol

Full size image

5 Discussion

We conclude the assessment of the performance of the new transient absorption machine with a discussion of the sensitivity. We expect that the noise measured at any individual pixel of the detector scales with the inverse of the square root of the number of photons collected by this particular detector element. This number of photons is proportional to the number M of events averaged, the size of the time window T selected for the streak image, and the width d of the slits of the spectrograph. The standard deviation should be a function of the wavelength since the intensity of the probe light is lower in the red region (λ > 650 nm) and highest in the visible range between 400 and 600 nm. Hence it should be possible to model the standard deviation according to

$$ \sigma(\lambda) = \sigma_0(\lambda) \left( \frac{T_0 d_0 M_0}{T d M}\right)^{1/2} $$
(25)

where T 0 is the time window, d 0 the slit width of the spectrograph, and M 0 the number of averaged events in a typical measurement taken as the reference. Figure 12 shows, in panel (a), the measured function σ0(λ) for T 0 = 10 μs, d 0 = 60 μm, and M 0 = 50. The function was obtained by a measurement on a cuvette filled with pure water and blocking the excitation laser. The standard deviation was calculated for each column of the data matrix, i.e., for all pixels belonging to the same wavelength. In the limit of zero slit widths the resolution of the streak camera CCD combination is ca. 2.5 pixels both in the time and the wavelength direction. We use a slit width of 30 μm for the streak camera, resulting in a width of 2.9 pixels for an infinitely fast (i.e., unresolved) event. For a given time window T the temporal resolution is hence δt = 0.00566 T. The spectral resolution increases linearly with the slit width d of the spectrograph according to δλ/[nm] = 2.1 + 0.0124 d/[μm]. With the settings mentioned above the time resolution is 57 ns and the spectral resolution is 2.9 nm. In this “standard experiment”, the noise is ca. 3.5 mOD on each pixel in the spectral range 350–500 nm. It should be noted that this noise can be further reduced by SVD analysis—without any loss in spectral or temporal resolution—by a factor of \(\sqrt{K/512}, \) where K is the number of significant components.

Fig. 12
figure 12

a Standard deviation σ0 for an individual data point (pixel) in the streak image for a measurement in a time window of T 0 = 10 μs, a monochromator slit of d 0 = 60 μm, and averaging over M 0 = 50 pump-probe pulse sequences. b The standard deviation scales with the inverse square root of T (triangles), d (squares), and M (circles)

Full size image

Panel (b) in Fig. 12 shows that the noise indeed scales with the inverse square root of T, d, and M. The standard deviation σ averaged over the wavelength interval 350–500 nm is plotted versus \(\sqrt{T_0/T}\) (triangles), \(\sqrt{d_0/d}\) (squares), and \(\sqrt{M_0/M}\) (circles). Error bars indicate the standard deviation of these errors in that spectral interval. All data points fall nicely on the same straight line. Hence Eq. 25 can be used in combination with the curve in Fig. 12a to estimate the noise for other settings of the apparatus. All these values refer to the same setting of the entrance slit of the streak camera (30 μm), and to the light intensity of our present pulsed Xe flash lamp. Even lower noise levels could be achieved by increasing the slit width of the streak camera (thereby sacrificing time resolution) or by employing a brighter flash lamp. We plan to use the latter option, in combination with a faster excitation laser, in order to access shorter time windows in the range 1–100 ns.

Recently, it has been proposed to measure transient absorptions in the microsecond domain with a fs-laser system [47]. These systems generate a white light continuum that can serve as the probe light. The duration of this probe pulse is in the 30–100 fs range; hence the time window in the μs range must be covered by consecutive measurements with appropriate time delay between pump and probe. This delay cannot be made by optical delay paths but has to be made electronically by synchronization of pump and probe to a master clock which is conveniently taken from the mode-locked seed laser. In order to fill 500 rows of the data matrix for 500 delay times the sample has to be excited 500 times. However, since both pump and probe light are coherent, they can be strongly focussed. Hence the excited volume is much smaller than in our streak camera setup, and one might expect that the fs experiment can be done with less amount of sample. This situation will now be examined.

We assume that the limiting factor to the experiment is the amount of sample that is damaged by pump laser and probe light. The amount of damage done by the pump laser is then estimated by considering the number of excited molecules N * in a volume of cross section A and length L, which is given by

$$ N^* = c^* L A M $$
(26)

where \(c^*\) is the concentration of excited molecules produced by a single pump laser pulse, and M is the number of excitations required to fill the whole data array. To permit a measurement of similar quality the optical density induced by the pump, given by \(E = \epsilon c^* L, \) should be the same in both setups. The ratio of the damage produced by the pump is then given by

$$ Q_{\mathrm{pump}} = \frac{N^*_{\mathrm{st}}}{N^*_{\mathrm{fs}}} = \frac{A_{\mathrm{st}}}{A_{\mathrm{fs}} M_{\mathrm{fs}}} $$
(27)

Here the subscripts st and fs refer to the streak camera and the femtosecond setup, respectively. The diameter of the excited volume is ca. 2 mm for the streak camera measurement, and ca. 120 μm for the fs measurement. With M = 500 rows in the data array we find Q pump ≈ 0.6, i.e., the damage done to a precious sample by the pump light is of similar magnitude in both experiments. The number of molecules destroyed in the sample by the probe light is proportional to the amount of probe light passed through the sample and the number of molecules in the illuminated volume. In order to have a similar S/N ratio in the two measurements we require that the same number P of probe photons arrive at the detector. This number is given by

$$ P_{\mathrm{st}} = I_{\mathrm{st}} A_{\mathrm{st}} T_{\hbox{W}} \eta $$
(28)
$$ P_{\mathrm{fs}} = I_{\mathrm{fs}} A_{\mathrm{fs}} \tau M \eta $$
(29)

where I is the light intensity, T W is the observed time window in the streak camera experiment, τ is the pulse duration in the fs experiment, A is the cross section of the excited sample, M is the number of rows in the data matrix, and η is the efficiency of detection. The damage D applied to the sample is given by the number of photons applied to the sample multiplied with the concentration and the probe volume,

$$ D_{\mathrm{st}} = P_{\mathrm{st}} c_{\mathrm{st}} A_{\mathrm{st}} L_{\mathrm{st}}\frac{T}{T_{\hbox{W}}} $$
(30)
$$ D_{\mathrm{fs}} = P_{\mathrm{fs}} c_{\mathrm{fs}} A_{\mathrm{fs}} L_{\mathrm{fs}} $$
(31)

where T is the duration of the white light flash in the streak camera setup. The ratio of damage done in both setups is then

$$ Q_{\mathrm{probe}} = \frac{D_{\mathrm{st}}}{D_{\mathrm{fs}}} = \frac{c_{\mathrm{st}} A_{\mathrm{st}} L_{\mathrm{st}} T}{c_{\mathrm{fs}} A_{\mathrm{fs}} L_{\mathrm{fs}} T_{\hbox{W}}} = \frac{A_{\mathrm{st}} T}{A_{\mathrm{fs}} T_{\hbox{W}}} $$
(32)

In the last part of Eq. 32 it was assumed that the concentrations in both experiments were chosen so that the same optical density is obtained. The result is similar to Eq. 27 except for the factor M in the denominator. The reason is that the same amount of probe light is passed through the sample in both experiments, but this is done in M increments in the fs-experiment. The ratio of the two cross sections is of the order of 100–300 in favor of the fs experiment. In the experimental section we have shown that the total damage done by the probe light in the streak camera experiment is about equal to the damage done by the pump light. Equation 32 shows that the streak camera experiment becomes less favorable when the time window T W is only a small fraction of the time duration T of the flash. This ratio could be improved when a fast switch is used to select only the required part from the white light flash, e.g. with a Pockels cell.

For measurements with protein samples an additional constraint on the experiments arises from the fact that these compounds can often only be produced in very small amounts and low concentrations. When using a flow cell the amount of solution required is similar for streak camera and fs experiments. However, due to the shorter light path in the fs experiments, the concentration and hence the absolute amount needs to be higher by at least a factor of 20. Producing an optical density of ca. 0.5 on a 500 μm path length requires a concentration of 0.8 mM for a flavoprotein (\(\epsilon \approx 1.2 \times 10^4\) M−1 cm−1). At this high concentrations proteins can aggregate or precipitate from the solution.

6 Summary

In summary, we have shown that the streak camera apparatus is capable of measuring fluorescence spectra and transient absorption spectra in a single excitation event for time windows T > 1 μs with a time resolution of δt ≈ T / 200. Our experience with one-dimensional measurements at a fixed wavelength is that the number of pump-probe pulse sequences required to obtain a reasonable monoexponential fit typically is M ≈ 100. Furthermore, measurements are not possible at wavelengths that overlap with the fluorescence. With the streak camera, we can measure over the full wavelength range and obtain the decay characteristics of the system for all these wavelengths with less pump-probe pulse sequences than required for a single one-dimensional measurement. The fluorescence spectrum is obtained as a byproduct. This is possible for two reasons: (1) The streak camera has a much larger dynamic range (10,000:1) compared with the typical dynamic range of a photomultiplier, and (2) the streak camera data are highly redundant. This more than compensates for the comparatively low S/N-ratio of each individual pixel. For example, filtering of the data matrix by singular value decomposition to the five most significant components is equivalent to averaging of 100 columns and 100 rows of the matrix without any loss in temporal or spectral resolution. We conclude that the streak camera setup yields transient absorption data with a multiplex factor of more than 100 compared wtih one-dimensional measurements of time traces at fixed wavelengths. In addition, we can measure transient absorption over the full wavelength range 350–750 nm also for systems with strong fluorescence.