1 Introduction

The generation and employment of terahertz (THz) waves for various applications are fast emerging as a frontline area of research. These waves are suitable for medical imaging, material diagnostics, explosives detection and spectroscopy [1–5]. Two routes have been pursued for the generation for THz: one, using relativistic electron beams, e.g., in free electron laser and rippled density plasma and second, using intense short pulse laser interaction with nonlinear dielectrics and plasmas [6, 7]. The laser-based techniques are relatively compact and are suitable for modest THz power generation [8]. Lasers produce odd harmonics in uniform plasma with power peaking at the third harmonic [9]. Various techniques are employed to enhance the intensity of high-order harmonics [10, 11]. The efficiency of energy conversion is low as the process is a nonresonant one due to the wave number mismatch. Application of a density ripple turns the process resonant, greatly enhancing the efficiency [12, 13]. Pathak et al. [14] have carried out particle in cell simulations of THz radiation generation in a plasma density ripple. Kumar et al. [15] have studied the excitation of terahertz surface plasmon using relativistic electron beams over a semiconductor surface. Kumar et al. [16] have reported an enhancement in nonlinear coupling due to cyclotron resonance. Sandhu et al. [17] have presented two-pulse time resolved second harmonic and hard X-ray generation in the interaction of an intense laser with a preplasma generated on a solid surface. Several other THz generation schemes have been studied theoretically while some experimentally or through PIC simulations [18–32].

Terahertz radiation in plasmas has been observed in many experiments using two-colour laser scheme [33–37]. Schwarz et al. [38] have studied the constructive effects of driving fields that are not monochromatic but contain its second harmonic. Xie et al. [39] have demonstrated that the four-wave mixing rectification is the main mechanism of THz wave generation in laser produced plasmas [40]. It was observed that the emitted THz radiation is consistent with four wave mixing in a plasma and shows characteristic intensity dependence proportional to \( I_{1}^{2} I_{2} \) and is maximized when the polarization of the lasers is aligned. An alternative model for two-color THz generation mechanism has been proposed by Penano et al. [41]. In this mechanism, the beating of the two laser beams creates a finite nonlinear current density due to large electron collisions driving the radiation in the THz regime. The proposed model has succeeded in explaining a number of properties of THz radiation observed in recent experiments [39].

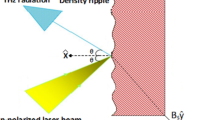
In this paper, we propose the employment of a density ripple of suitable wavenumber to produce THz radiation via second-order nonlinear mixing of two lasers, a fundamental laser and a frequency shifted second harmonic in a collision less plasma. A density rippled plasma can be generated by various schemes [11, 42, 43]. The density ripple of suitable wave number \( \vec{q} \) converts the THz generation process into a resonant process, greatly enhancing the efficiency. The physics of process is as follows. A linearly polarized laser of frequency \( \omega_{1} \) and wave vector \( \vec{k}_{1} \), and its frequency shifted second harmonic \( \omega_{2\,} ,\,\vec{k}_{2} \) is passed through an under dense plasma with density ripple \( n_{q} \) of wave number \( \vec{q} \). It imparts oscillatory velocities \( \vec{V}_{{\omega_{1} ,k_{1} }} ,\,\vec{V}_{{\omega_{2} ,k_{2} }} \) to electrons. It exerts ponderomotive forces on electrons at \( (2\omega_{1} ,\,2\vec{k}_{1} ) \) and \( (\omega_{1} - \omega_{2} ,\vec{k}_{1} - \vec{k}_{2} ) \) producing charge density oscillations at these frequencies. In the presence of a density ripple, they beat with \( n_{q} \) to produce density oscillations at \( (\omega_{1} - \omega_{2} ),(\vec{k}_{1} - \vec{k}_{2} - \vec{q})\,{\text{and}}\,(2\omega_{1} ,\,2\vec{k}_{1} - \vec{q}) \). These density oscillations beat with the oscillatory velocities at \( \vec{V}_{{\omega_{1} ,k_{1} }} ,\,\vec{V}_{{\omega_{2} ,k_{2} }}^{*} \)respectively to produce a nonlinear current, resonantly driving the terahertz when \( (2\vec{k}_{1} - \vec{k}_{2} - \vec{q}) \) equals the terahertz wave number \( \vec{k} \). This gives rise to stronger radiation contrary to the case of homogeneous plasma where this resonance is missing. The plan of the paper is as follows. In Sect. 2, we calculate the charge density oscillations by ponderomotive forces leading to the requisite nonlinear current for radiation generation. In Sect. 3, the power of THz radiation evaluated and variation in conversion efficiency is obtained w. r. t. terahertz frequency. In Sect. 4, results are discussed.

2 Charge density oscillations and nonlinear current

Let us consider a rippled density plasma with electron density.

$$ n_{e} = n_{0} + n_{q} , \\ n_{q} = n_{q0} \,{\text{e}}^{iqz}.$$
(1)

Two collinear laser beams propagate through it with electric and magnetic fields

$$ \vec{E}_{j} = \hat{e}_{j} \,{\text{A}}_{j} \,{\text{e}}^{{ - i(\omega_{j} t - k_{j} z)}} $$
(2)
$$ \vec{B}_{j} = \,(\vec{k}_{j} \times \vec{E}_{j} )/\omega_{j} , $$
(3)

where j = 1, 2 represent the first and the second laser with respective dispersion relations as

$$ k_{j} = \frac{{\omega_{j} }}{c}\left( {1 - \frac{{\omega_{p}^{2} }}{{\omega_{j}^{2} }}} \right)^{1/2} \approx \frac{{\omega_{j} }}{c}\quad {\text{and }}\omega_{2} = 2\omega_{1} - \omega $$
(4)

The phase matching conditions for resonant excitation of terahertz generation are

$$ 2\omega_{1} - \omega_{2} = \omega , $$
(5)

\( 2k_{1} - k_{2} - q = k \), where

$$ k = (\omega /c)\left( {1 - (\omega_{\text{p}}^{2} /\omega^{2} )} \right)^{1/2} . $$
(6)

These demand

$$ \begin{gathered} q = 2k_{1} - k_{2} - k \hfill \\ \,\,\,\, = \frac{\omega }{c} \left[1 - \left(1 - \left( {1 - (\omega_{\text{p}}^{2} /\omega_{{}}^{2} )} \right)^{1/2} \right)\right]. \hfill \\ \end{gathered} $$
(7)

In Fig. 1 we have plotted the requisite ripple wave number, normalized to \( c/\omega \) as a function of \( \omega_{\text{P}} \). As \( \omega_{\text{P}} \) increases one requires shorter wavelength ripple to compensate for phase mismatch.

The lasers impart oscillatory velocities to electrons

$$ \vec{V}_{1} = \frac{{e\vec{E}_{1} }}{{mi\omega_{1} }}, $$
(8)
$$ \vec{V}_{2} = \frac{{e\vec{E}_{2} }}{{mi\omega_{2} }} . $$
(9)

The ponderomotive force on electrons due to the two lasers is

$$ \vec{F}_{\text{P}} = m(\vec{V}_{1} + \vec{V}_{2} ). \nabla (\vec{V}_{1} + \vec{V}_{2} ) - e[(\vec{V}_{1} + \vec{V}_{2} ) \times (\vec{B}_{1} + \vec{B}_{2} )] $$
(10)

where real parts of \( \vec{V}_{1} ,\,\,\vec{V}_{2} ,\,\,\vec{B}_{1} \,\,{\text{and}}\,\,\vec{B}_{2} \) are implied.

The first term in \( \vec{F}_{\text{P}} \) is zero as the oscillatory velocities are transverse to the direction of propagation. The second term on using the complex number identity \( Re\vec{A} \times Re\vec{B} \equiv 1/2Re[\vec{A} \times \vec{B} + \vec{A} \times \vec{B}^{ * } ] \) yields

$$ \begin{gathered} \vec{F}_{\text{P}} = - eRe(\vec{V}_{1} + \vec{V}_{2} ) \times Re({\vec{{B}}}_{1} + {\vec{{B}}}_{2} )] \hfill \\ \quad \; = - \frac{e}{2}Re[(\vec{V}_{1} + \vec{V}_{2} ) \times (\vec{B}_{1} + \vec{B}_{2} ) + (\vec{V}_{1} + \vec{V}_{2} ) \times ({\vec{{B}}}_{1}^{*} + {\vec{{B}}}_{2}^{*} )] \hfill \\ \end{gathered} $$
(11)

The relevant components of ponderomotive force at \( (2\omega_{1} ,\,2k_{1} ) \) and \( (\omega_{1} - \omega_{2} ,\,k_{1} - k_{2} ) \) are

$$ \begin{gathered} \vec{F}_{{P(2\omega_{1} ,\,2k_{1} )}} = - \frac{e}{2}Re[(\vec{V}_{1} \times {\vec{{B}}}_{1} )] = \frac{{ - e^{2} E_{1}^{2} (2\vec{k}_{1} )}}{{2mi\omega_{1}^{2} }}, \hfill \\ \end{gathered} $$
(12)
$$ \begin{aligned} \vec{F}_{{(\omega_{1} - \omega_{2} ,\,k_{1} - k_{2} )}} & = - \frac{e}{2}Re[(\vec{V}_{1} \times \vec{B}_{2}^{*} ) + (\vec{V}_{2}^{*} \times {\vec{{B}}}_{1} )] \\ \,\, = \frac{{e^{2} (\vec{E}_{1} \cdot \vec{E}_{2}^{*} )(\vec{k}_{1} - \vec{k}_{2} )}}{{2mi\omega_{1} \omega_{2} }}. \\ \end{aligned} $$
(13)

\( \vec{F}_{{{\text{P}}(2\omega_{1} ,\,2k_{1} )}} \) and the self generated field \( e\vec{E}_{{(2\omega_{1} ,\,2k_{1} )}} \) imparts an oscillatory velocity to electrons at \( (2\omega_{1} ,\,2k_{1} ) \), in compliance with the equation of motion,

$$ m\frac{\partial }{\partial t}\vec{V}_{{(2\omega_{1} ,\,2k_{1} )}} = \vec{F}_{{(2\omega_{1} ,\,2k_{1} )}} - e\vec{E}_{{(2\omega_{1} ,\,2k_{1} )}} $$
(14)
$$ \vec{V}_{{2\omega_{1} ,2k_{1} }} = \frac{{ - e\vec{E}_{{2\omega_{1} ,2\vec{k}_{1} }} }}{{mi\omega_{1} }} - \frac{{ - e^{2} E_{1}^{2} (2\vec{k}_{1} )}}{{2m^{2} i\omega_{1}^{3} }} $$
(15)

This velocity is longitudinal (|| \( \vec{k}_{1} \)), hence gives rise to density oscillations at \( (2\omega_{1} ,\,2k_{1} ) \), governed by the equation of continuity,

$$ \frac{\partial }{\partial t}n_{{(2\omega_{1} ,\,2k_{1} )}} + \nabla \cdot (n_{0}^{0} \,\vec{V}_{{(2\omega_{1} ,\,2k_{1} )}} ) = 0 , $$
(16)
$$ n_{{(2\omega_{1} ,\,2k_{1} )}} = \frac{{n_{0}^{0} \,2\vec{k}_{1} \cdot \vec{V}_{{(2\omega_{1} ,\,2k_{1} )}} }}{{2\,i\,\omega_{1} }} $$
(17)

Using Eq. (17) in the Poisson’s equation, \( \nabla \cdot \vec{E}_{{2\omega_{1} ,2k_{1} }} = ( - e/\varepsilon_{0} )n_{{2\omega_{1} ,2k_{1} }} \), one obtains

$$ \vec{E}_{{(2\omega_{1} ,\,2k_{1} )}} = \hat{z}\,( - e/\varepsilon_{0} )\frac{{n_{{(2\omega_{1} ,\,2k_{1} )}} }}{{i\,2k_{1} }} $$
(18)

Using Eqs. (15), (17) and (18) on may write

$$ n_{{2\omega_{1} ,2k_{1} - q}} = \frac{{ - n_{q}^{*} e^{2} k_{1}^{2} E_{1}^{2} }}{{4m^{2} \omega_{1}^{4} \left( {1 - \frac{{\omega_{p}^{2} }}{{4\omega_{1}^{2} }}} \right)}} $$
(19)

In the presence of density ripple of wave vector \( \vec{q} \), the ponderomotive force induced oscillatory velocity gives rise to density oscillation at \( (2\omega_{1} ,\,2k_{1} - q) \). Combining the effect of self generated field, \( \nabla \cdot \vec{E}_{{2\omega_{1} ,2k_{1} - q}} = ( - e/\varepsilon_{0} )n_{{2\omega_{1} ,2k_{1} - q}} \), due to this oscillation, one may write the equation of continuity as

$$ \frac{\partial }{\partial t}n_{{(2\omega_{1} ,\,2k_{1} - q)}} + \nabla \cdot (n_{0}^{0} \,\vec{V}_{{(2\omega_{1} ,\,2k_{1} - q)}} + n_{q}^{*} \,\vec{V}_{{(2\omega_{1} ,\,2k_{1} )}} \,) = 0, $$
(20)

where

$$ \vec{V}_{{2\omega_{1} ,2k_{1} - q}} \equiv - e\vec{E}_{{2\omega_{1} ,2k_{1} - q}} /mi\omega_{1}.$$
(21)

Using the same procedure, the ponderomotive force at \( (\omega_{1} - \omega_{2} ,\vec{k}_{1} - \vec{k}_{2} ) \) gives rise to oscillatory velocity to electrons driving the density perturbation at the same frequency

$$ n_{{\omega_{1} - \omega_{2} ,k_{1} - k_{2} }} = \frac{{ - n_{0}^{0} e^{2} (\vec{E}_{1} \cdot \vec{E}_{2}^{*} )\left| {\vec{k}_{1} - \vec{k}_{2} } \right|^{2} }}{{4m^{2} \omega_{1} \omega_{2} [(\omega_{1} - \omega_{2} )^{2} - \omega_{\text{P}}^{2} ]}} $$
(22)

The ponderomotive force drive oscillatory velocity beats with the density ripple to drive a density oscillation at \( (\omega_{1} - \omega_{1} ,\vec{k}_{1} - \vec{k}_{2} - \vec{q}) \)

$$ n_{{\omega_{1} - \omega_{2} ,k_{1} - k_{2} - q}} = \frac{{n_{q}^{*} e^{2} (\vec{E}_{1} \cdot \vec{E}_{2}^{*} )\left| {\vec{k}_{1} - \vec{k}_{2} } \right|^{2} }}{{4m^{2} \omega_{1} \omega_{2} [(\omega_{1} - \omega_{2} )^{2} - \omega_{\text{P}}^{2} ]}} $$
(23)

The density perturbations beat with the oscillatory velocities given by Eqs. (8) and (9) to yield a nonlinear current at (\( 2\omega_{1} - \omega_{2} ,\,2\vec{k}_{1} - \vec{k}_{2} - \vec{q} \))

$$ \begin{aligned} \vec{J}_{\omega ,\,k}^{NL} = - \frac{1}{2}n_{{(2\omega_{1} ,\,2k_{1} - q)}} e{\bf V}_{{\omega_{2} ,k_{2} }}^{*} - \frac{1}{2}n_{{(\omega_{1} - \omega_{2} ),(k_{1} - k_{2} - q)}} e{\bf V}_{{\omega_{1} ,k_{1} }} \\ \, = \frac{{n_{q}^{*} e^{2} k_{1}^{2} E_{1}^{2} }}{{4m^{2} \omega_{1}^{4} \left( {1 - \frac{{\omega_{p}^{2} }}{{4\omega_{1}^{2} }}} \right)}}\,\frac{{e^{2} \vec{E}_{2}^{*} }}{{mi\omega_{2} }} + \frac{{n_{q}^{*} e^{2} (\vec{E}_{1} \cdot \vec{E}_{2}^{*} )\left| {\vec{k}_{1} - \vec{k}_{2} } \right|^{2} }}{{4m^{2} \omega_{1} \omega_{2} [(\omega_{1} - \omega_{2} )^{2} - \omega_{\text{P}}^{2} ]}}\,\frac{{e^{2} \vec{E}_{1}^{{}} }}{{mi\omega_{1} }} \\ \end{aligned} $$
(24)

3 Terahertz radiation

The nonlinear terahertz current generates radiation at terahertz frequency \( (\omega ,\,\vec{k}) \). The Maxwell’s equations are,

$$ \nabla \times \vec{E}_{\omega ,\,\,k} = - i\omega \mu_{0} \vec{H}_{\omega ,\,k} $$
(25)
$$ \nabla \times \vec{H}_{\omega ,\,\,k} = \vec{J} + \varepsilon_{0} \frac{{\partial \vec{E}_{\omega ,\,\,k} }}{\partial t} $$
(26)

The total current density is a combination of linear and nonlinear parts given as

$$ \vec{J} = \vec{J}^{\text{L}} + \vec{J}_{\omega ,\,k}^{\text{NL}} $$
(27)
$$ \frac{{\partial^{2} }}{{\partial z^{2} }}\vec{E}_{\omega ,\,k} + \left( {\frac{{\omega^{2} - \omega_{p}^{2} }}{{c^{2} }}} \right)\vec{E}_{\omega ,\,k} = \frac{ - i\omega }{{c^{2} \varepsilon_{0} }}\vec{J}_{\omega ,\,k}^{\text{NL}} $$
(28)

We express \( E_{\omega ,\,k} \) as

$$ \vec{E}_{\omega ,\,k} = \vec{A}_{\omega ,\,k} (z){\text{e}}^{{ - i\left( {\omega t - kz} \right)}} $$
(29)

then Eq. (28) gives the evolution of slowly varying amplitude

$$ \frac{{\partial \vec{A}_{\omega ,\,k} }}{\partial \,z} = \frac{\omega }{{2c^{2} \varepsilon_{0} k}}\left[ {\frac{{n_{q}^{*} e^{2} k_{1}^{2} E_{1}^{2} }}{{4m^{2} \omega_{1}^{4} \left( {1 - \frac{{\omega_{\text{p}}^{2} }}{{4\omega_{1}^{2} }}} \right)}}\frac{{e^{2} \vec{E}_{2}^{*} }}{{mi\omega_{2} }} + \frac{{n_{q}^{*} e^{2} (\vec{E}_{1} \cdot \vec{E}_{2}^{*} )\left| {\vec{k}_{1} - \vec{k}_{2} } \right|^{2} }}{{4m^{2} \omega_{1} \omega_{2} [(\omega_{1} - \omega_{2} )^{2} - \omega_{\text{P}}^{2} ]}}\frac{{e^{2} \vec{E}_{1}^{{}} }}{{mi\omega_{1} }}} \right] $$
(30)

If the length of the plasma is shorter than a damping length, Eq. (30) gives

$$ \vec{A}_{\omega ,\,k} = \frac{\omega }{{2c^{2} \varepsilon_{0} k}}\left[ {\frac{{n_{q}^{*} e^{2} k_{1}^{2} E_{1}^{2} }}{{4m^{2} \omega_{1}^{4} \left( {1 - \frac{{\omega_{\text{p}}^{2} }}{{4\omega_{1}^{2} }}} \right)}}\frac{{e^{2} \vec{E}_{2}^{*} }}{{m\,i\omega_{2} }} + \frac{{n_{q}^{*} e^{2} (\vec{E}_{1} \cdot \vec{E}_{2}^{*} )\left| {\vec{k}_{1} - \vec{k}_{2} } \right|^{2} }}{{4m^{2} \omega_{1} \omega_{2} [(\omega_{1} - \omega_{2} )^{2} - \omega_{\text{P}}^{2} ]}}\frac{{e^{2} \vec{E}_{1}^{{}} }}{{m\,i\omega_{1} }}} \right]\,z\,. $$
(31)

If one includes linear damping of the terahertz wave, Eq. (30) must include a term \( \vec{A}_{\omega ,\,k} \) \( k_{i} \), on the left-hand side, where \( k_{i} \equiv (\nu /2c)(\omega_{\text{P}}^{2} /\omega^{2} ) \) and \( \nu \) is the electron collision frequency. The terahertz wave saturates at a value

$$ \vec{A}_{\omega ,\,k} = \frac{\omega }{{2c^{2} \varepsilon_{0} kk_{i} }}\left[ {\frac{{n_{q}^{*} e^{2} k_{1}^{2} E_{1}^{2} }}{{4m^{2} \omega_{1}^{4} \left( {1 - \frac{{\omega_{\text{p}}^{2} }}{{4\omega_{1}^{2} }}} \right)}}\frac{{e^{2} \vec{E}_{2}^{*} }}{{mi\omega_{2} }} + \frac{{n_{q}^{*} e^{2} (\vec{E}_{1} \cdot \vec{E}_{2}^{*} )\left| {\vec{k}_{1} - \vec{k}_{2} } \right|^{2} }}{{4m^{2} \omega_{1} \omega_{2} [(\omega_{1} - \omega_{2} )^{2} - \omega_{\text{P}}^{2} ]}}\frac{{e^{2} \vec{E}_{1}^{{}} }}{{mi\omega_{1} }}} \right]\,. $$
(32)

One may note that the THz amplitude depends on the angle between \( \vec{E}_{1} \) and \( \vec{E}_{2} \). Maximum THz generation occurs when \( \vec{E}_{1} ||\vec{E}_{2} \). In this case THz field is also polarized \( ||\,\,\,\vec{E}_{1} ,\,\,\vec{E}_{2} \). The THz amplitude falls off rather rapidly as \( \omega /\omega_{P} \) increases beyond 1. As \( \omega /\omega_{P} \) acquires values ~2, the rate of decrease is less rapid. It is sensitive to the angle between the polarizations of \( \omega_{1} \) and \( \omega_{2} \) radiations. This result is in agreement with the experimental results obtained by Xie et al. [39]. They measured the resultant state of THz polarization by changing the state of polarization of the beams. The resultant THz has maximum amplitude when both the beams are in the same state of polarization. One may also note from Eq. (30) that the THz power scales linearly with the intensity of \( \omega_{2} \) laser and as a square of the intensity of the fundamental \( \omega_{1} \).

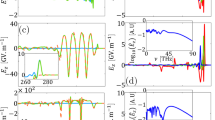
We have carried out numerical calculations for a typical set of parameters of practical interest: \( \lambda_{1} \equiv 2\pi c/\omega_{1} = 1\;\upmu{\text{m}}, \) \( \lambda_{2} \equiv 2\pi c/\omega_{2} \sim 0.5\;\upmu{\text{m}},\, \) \( \omega_{P}^{{}} /2\pi = 0.6\;{\text{THz}}, \) \( n_{q0} /n_{0}^{0} = 0.2, \) \( \,\beta \equiv {{|E_{2} |} \mathord{\left/ {\vphantom {{|E_{2} |} {|E_{1} |}}} \right. \kern-0pt} {|E_{1} |}} = 0.5 \) and \( (2\omega_{1} - \omega_{2} )/2\pi = \omega /2\pi \simeq (0.7 - 5) \)THz. We have plotted the THz amplitude normalized to incident laser amplitude as a function of THz frequency (Fig. 2). It is maximum for \( \vec{E}_{1} ||\vec{E}_{2} \). As the angle (\( \theta \)) between \( \vec{E}_{1} \) and \( \vec{E}_{2} \) increases is the conversion efficiency falls. The orientation of THz field is in between the orientation of \( \vec{E}_{1} \) and \( \vec{E}_{2} \).

Fig. 1
figure 1

The phase matching ripple density wave vector q normalized to \( \omega /c \) for background plasma frequency \( \omega_{p} = 3.2 \times 10^{12}\,{\rm Hz} \) (solid, Red) and \( \omega_{p} = 4.8 \times 10^{12}\;{\text {Hz}} \) (dashed, Green)

Full size image
Fig. 2
figure 2

Radiated THz intensity is plotted w. r. t. THz frequency for different relative angles (\( \theta \)) between its polarizations. The chosen set of parameters is \( e\vec{E}_{1} /mi\omega_{1} c = 0.1\sim 0.2, \) \( n_{q} /n_{0}^{0} = 0.2, \) \( \lambda = 1.064\;\upmu{\text{m}}, \) and \( \beta = 0.5 \). a \( \theta = 30^{ \circ } \), b \( \theta = 45^{ \circ } \), c \( \theta = 60^{ \circ } \), d \( \theta = 75^{ \circ } \), and e \( \theta = 90^{ \circ } \)

Full size image

4 Discussion

Plasma appears as an efficient nonlinear medium for THz generation by two-colour laser scheme. A pre-existing density ripple causes phase matching that enhances the THz generation efficiency. The requisite ripple wave number increases with the plasma density. The THz power scales directly as the square of ripple amplitude. Density ripple can be created in a laser produced plasma channel by inserting a ring grating before an axicon [42]. Similarly, modifying the flow of clustered jet by putting periodically spaced wire also generates modulated plasma waveguides with periods as low 50 μm [43]. The parameters are suitable for resonant excitation of THz wave in the range 0.5–6 THz. The THz power conversion efficiency decreases with the THz frequency. The efficiency is sensitive to the angle between the polarizations of the mixing lasers. It is maximum when the laser polarizations are aligned. The prescribed model also reflects the known characteristic dependence on laser intensity and polarization of a recent experiment. It carries twin benefits of plasma as background supporting broad range of frequencies and density modulation for tunability.