1 Introduction

Laguerre–Gaussian (LG) beam is a typical higher-order mode in cylindrically symmetric optical cavity [1]. In the past decades, numerous efforts have been devoted to LG beam due to its important applications in particle trapping, gravitational wave detectors, electron acceleration, free-space optical communications, atom trapping and guiding [2–6]. Different methods have been proposed to generate LG beam [6–9]. Paraxial propagation properties of LG beam have been explored in detail [10–14]. Recently, partially coherent LG beam was introduced as a natural extension of coherent LG beam to the stochastic domain [15, 16]. The propagation properties of a partially coherent LG beam in free space were investigated in detail [15, 16], and it was found that the propagation properties of a partially coherent LG beam are much different from that of a coherent LG beam. The evolution properties of a partially coherent LG beam in turbulent atmosphere were reported in [17–19], and it was revealed that a partially coherent LG beam has advantage over a coherent LG beam for reducing or overcoming turbulence-induced degradation, thus it has important application in free-space optical communication. In this study, we report experimental generation of a partially coherent LG0l beam, and study its focusing properties both theoretically and experimentally. Some useful results are found.

2 Model for a partially coherent Laguerre–Gaussian beam and its paraxial propagation

In this section, we outline briefly the definition of a partially coherent LG beam and its paraxial propagation.

The second-order correlation properties of a partially coherent beam, in space-frequency domain, can be characterized by the cross-spectral density (CSD) of the electric field, defined by the formula [20]:

$$ W(x_{1} ,y_{1} ,x_{2} ,y_{2} ) = \left\langle {E(x_{1} ,y_{1} )E^{*} (x_{2} ,y_{2} )} \right\rangle , \, $$
(1)

where \( (x_{1 \, } , { }y_{1} ) \) and \( (x_{2 \, } , { }y_{2} ) \) denote the coordinates of two arbitrary points at the source plane. Here the asterisk denotes the complex conjugate and the angular brackets denote ensemble average.

In the cylindrical coordinate system, the CSD of a partially coherent LG beam radiated from a Schell-model source can be expressed as [16]

$$ W(r_{1} ,r_{2} ,\varphi_{1} ,\varphi_{2} ) = \left( {\frac{{\sqrt 2 r_{1} }}{{\omega_{0} }}} \right)^{l} \left( {\frac{{\sqrt 2 r_{2} }}{{\omega_{0} }}} \right)^{l} L_{p}^{l} \left( {\frac{{2r_{1}^{2} }}{{\omega_{0}^{2} }}} \right)L_{p}^{l} \left( {\frac{{2r_{2}^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( { - \frac{{r_{1}^{2} }}{{\omega_{0}^{2} }} - \frac{{r_{2}^{2} }}{{\omega_{0}^{2} }}} \right)\exp (il\varphi_{1} - il\varphi_{2} )\; \times \exp \left[ { - \frac{{r_{1}^{2} + r_{2}^{2} - 2r_{1} r_{2} \cos (\varphi_{1} - \varphi_{2} )}}{{2\sigma_{g}^{2} }}} \right], $$
(2)

where r and φ are the radial and azimuthal (angle) coordinates, \( \omega_{0} \) and \( \sigma_{g} \) are the transverse beam size and spatial coherence width, respectively, \( L_{p}^{l} \) denotes the Laguerre polynomial with mode orders p and l. Under the condition of \( p = 0 \) and \( l = 0 \), Eq. (2) reduces the following expression for the CSD of a Gaussian Schell-model (GSM) beam [20, 21]

$$ W(r_{1} ,r_{2} ,\varphi_{1} ,\varphi_{2} ) = \exp \left[ { - \frac{{r_{1}^{2} }}{{\omega_{0}^{2} }} - \frac{{r_{2}^{2} }}{{\omega_{0}^{2} }} - \frac{{r_{1}^{2} + r_{2}^{2} - 2r_{1} r_{2} \cos \left( {\varphi_{1} - \varphi_{2} } \right)}}{{2\sigma_{g}^{2} }}} \right] \, $$
(3)

Within the validity of the paraxial approximation, the paraxial propagation of the CSD of a partially coherent beam through an aligned ABCD optical system in free space can be studied by the following generalized Collins formula [16]

$$ W(\rho_{1} ,\rho_{2} ,\theta_{1} ,\theta_{2} ) = \left( {\frac{1}{\lambda \left| B \right|}} \right)^{2} \int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {W(r_{1} ,r_{2} ,\varphi_{1} ,\varphi_{2} )} } } } \times \exp \left[ { - \frac{ik}{2B}(Ar_{1}^{2} - 2r_{1} \rho_{1} \cos \left( {\varphi_{1} - \theta_{1} } \right) + D\rho_{1}^{2} )} \right]{\kern 1pt} \times {\kern 1pt} \exp \left[ {\frac{ik}{{2B^{*} }}\left( {A^{*} r_{2}^{2} - 2r_{2} \rho_{2} \cos (\varphi_{2} - \theta_{2} ) + D^{*} \rho_{2}^{2} } \right)} \right] \, d\varphi_{1} \,d\varphi_{2} \,dr_{1} \,dr_{2} , \, $$
(4)

where A, B, C and D are the transfer matrix elements of optical system, \( k = 2\pi /\lambda \) is the wave number with \( \lambda \) being the wavelength. Substituting Eq. (2) into Eq. (4), we can obtain the analytical propagation formula (Eq. (10) of [16]) for a partially coherent LG beam through a paraxial ABCD optical system. Numerical results in [16] have shown that the propagation properties of a partially coherent LG beam are much different from that of a coherent LG beam, and we can shape the beam profile of a partially coherent LG beam by varying its initial spatial coherence.

3 Experimental setup and experimental results

In this section, we report experimental generation of a partially coherent \( {\text{LG}}_{0l} \) beam, and study its focusing properties both experimentally and theoretically.

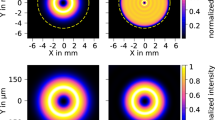
Figure 1 shows our experimental setup for generating a partially coherent \( {\text{LG}}_{0l} \) beam and measuring its focused intensity. A laser beam generated by a solid-state laser (\( \lambda = 532\,{\text{nm}} \)) is focused by a thin lens (L1), and then illuminates a rotating ground-glass disk (RGGD), producing a partially coherent beam with Gaussian statistics. After passing through the thin lens L1 and the Gaussian amplitude filter (GAF), the transmitted beam becomes a GSM beam, whose intensity and degree of coherence satisfy Gaussian distribution. The L1 is used to control the focused beam spot size on the RGGD. The L2 is used to collimate the transmitted light, and the GAF is used to convert the intensity of the transmitted light into a Gaussian profile. The generated GSM beam goes toward a spatial light modulator (SLM), which acts as a grating with fork pattern designed by the method of computer-generated holograms. The first-order diffraction pattern of the beam reflected from the SLM (Holoeye, PLUTO) is regarded as a partially coherent \( {\text{LG}}_{0l} \) beam, and is selected out by a circular aperture. The order \( l \) of the generated beam equals to the number of dislocations in the grating [9], thus we can generate partially coherent \( {\text{LG}}_{0l} \) beam with different \( l \) by introducing different fork patterns onto the SLM. The SLM is located just behind the GAF, so the spatial coherence width of the partially coherent \( {\text{LG}}_{0l} \) beam approximately equals to that of the GSM beam. The partially coherent \( {\text{LG}}_{0l} \) beam first passes through a thin lens L3 with focal length \( f = 32\,{\text{cm}} \), and then arrives at the beam profile analyzer (BPA), which measures the focused intensity.

Fig. 1
figure 1

Experimental setup for generating a partially coherent \( {\text{LG}}_{0l} \) beam and measuring its focused intensity. DPSSL diode-pumped solid-state laser, L 1 , L 2 , L 3 thin lenses; RGGD rotating ground-glass disk, GAF Gaussian amplitude filter, SLM spatial light modulator, CA circular aperture, BPA beam profile analyzer, PC 1 , PC 2 personal computers

Full size image

The CSD of the generated GSM beam is given by Eq. (3). The parameter \( \omega_{0} \) of the generated GSM beam is determined by the transmission function of the GAF and equals to 2 mm, \( \sigma_{g} \) is determined by the focused beam spot size on the RGGD and the roughness of the RGGD together. The roughness of the RGGD is fixed in our experiment, and \( \sigma_{g} \) is mainly modulated by varying the focused beam spot size on the RGGD. Here, we use the method proposed in [21] to measure \( \sigma_{g} \). As shown in [21], the GSM beam is split into two distinct imaging optical paths by a beam splitter, then, the transmitted beam and reflected beam go to two single-photon detectors, respectively. The value of \( \sigma_{g} \) can be obtained by measuring the fourth-order correlation function (FOCF) between the detectors based on the internal relation between the second-order correlation function and the FOCF of the GSM beam [20]. In our experiment, we choose four different values of \( \sigma_{g} \) (\( \sigma_{g} = \infty ,\,1.51{\kern 1pt} {\text{mm}},\,0.85{\kern 1pt} {\text{mm}},\,0.49{\kern 1pt} {\text{mm}} \)) to generate a partially coherent \( {\text{LG}}_{0l} \) beam with different spatial coherences. For the case of \( \sigma_{g} = \infty \), the RGGD is removed.

The transfer matrix between the SLM and the BPA reads as

$$ \left( {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 & f \\ { - 1/f} & {1 - s/f} \\ \end{array} } \right). \, $$
(5)

With the help of Eq. (5), the obtained propagation formula (Eq. (10) of [16]) and the measured beam parameters, we can simulate the focusing properties of the generated partially coherent \( {\text{LG}}_{0l} \) beam.

Figure 2 shows our experimental results of the focused intensity and the corresponding cross line (dotted curve) of the generated partially coherent \( {\text{LG}}_{0l} \) beam with l = 3 for four different values of \( \sigma_{g} \). For the convenience of comparison, the corresponding results (solid curves) calculated by theoretical formulae are also shown in Fig. 2. Figure 2 shows that the focusing properties of a partially coherent \( {\text{LG}}_{0l} \) beam are much different from that of a coherent \( {\text{LG}}_{0l} \) beam (\( \sigma_{g} = \infty \)) and are closely determined by its initial spatial coherence. The focused coherent \( {\text{LG}}_{0l} \) beam has a dark hollow (DH) beam spot (see Fig. 2a), which is similar to its source intensity. The beam profile of the focused partially coherent \( {\text{LG}}_{0l} \) beam varies as its initial spatial coherence varies (see Fig. 2b–d). For suitable value of \( \sigma_{g} \), a focused flat-topped (FT) beam spot can be formed (see Fig. 2c). With the further decrease of \( \sigma_{g} \), a focused Gaussian beam spot is formed (see Fig. 2d). Figure 2 shows that there is a small deviation between the experimental results and theoretical results. This small deviation is caused by the finite confinement of the circular aperture (see Fig. 2), which is used to select the first-order diffraction pattern of the beam from the SLM. Thus, our experimental results agree reasonably (not exactly) well with the theoretical predictions. Our results will be useful for trapping different particles. It is known that FT or Gaussian beam spot is used for trapping a particle with a refractive index larger than that of the ambient and a DH beam spot is used for trapping a particle with refractive index smaller than that of the ambient. Thus, it is possible for us to use one optical-trap system to trap two types of particles with the help of a focused LG0l beam through varying its initial spatial coherence.

Fig. 2
figure 2

Experimental results of the focused intensity and the corresponding cross line (dotted curve) of the generated partially coherent \( {\text{LG}}_{0l} \) beam with \( l = 3 \) for four different values of \( \sigma_{g} \). The solid curves are calculated by theoretical formulae

Full size image

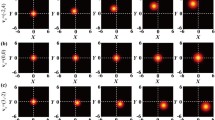
To learn about the influence of the beam order \( l \) on the focusing properties, we also measure the focused intensity of partially coherent \( {\text{LG}}_{0l} \) beams with \( l \) = 1, 3, 7 as shown in Fig. 3. Figure 3 shows that the dark size of the focused beam spot increases as the beam order \( l \) increases when \( \sigma_{g} \) is large (see Fig. 3a–d). With the decrease of \( \sigma_{g} \), the DH beam profile gradually disappears. We note that the DH beam profile of the partially coherent \( {\text{LG}}_{0l} \) beam with large \( l \) disappears much slower than that with small \( l \) (see Fig. 3e–h), which means an \( {\text{LG}}_{0l} \) beam with larger \( l \) is less affected when its spatial coherence is decreased. This phenomenon can be physically explained by the fact that the mechanism of competition between the random phase and the vortex phase (determined by the beam order \( l \)) of a \( {\text{LG}}_{0l} \) beam determines its focused beam profile. The random phase imposed by the RGGD in our experiment degrades the spatial coherence of the \( {\text{LG}}_{0l} \) beam, which results in distorting the focused DH beam profile. The vortex phase imposed by the SLM plays a role of keeping the focused DH beam profile invariant. When the beam order \( l \) is small, the effect of the random phase plays a dominant role. With the increase of the beam order \( l \), the vortex phase gradually plays a dominant role. Thus, the LG beam with larger beam order \( l \) is less affected when its spatial coherence is degraded. Our results will be useful for free-space optical communications, where the atmospheric turbulence inevitably reduces the spatial coherence of the LG beam during its propagation in turbulent atmosphere.

Fig. 3
figure 3

Experimental results of the focused intensity and the corresponding cross line of the generated partially coherent \( {\text{LG}}_{0l} \) beams with \( l = 1,3,7 \) for two different values of \( \sigma_{g} \)

Full size image

4 Conclusion

In conclusion, we have successfully carried out experimental generation of a partially coherent \( {\text{LG}}_{0l} \) beam with variable spatial coherence, and studied its focusing properties both experimentally and theoretically. Our results show that we can obtain focused DH or FT or Gaussian beam spot by varying the initial spatial coherence, which is useful for particle trapping. We also find that an \( {\text{LG}}_{0l} \) beam with larger \( l \) is useful for free-space optical communications.