1 Introduction

Space ground laser communication has been the focus of many researchers since many decades [1–3]. In such a link, atmospheric turbulence-induced fading and path losses are considered to be the main obstacles causing detection difficulties at the receiver end.

Improvement techniques have been analyzed since then such as relay-assisted transmitters and spatially diverse multi transmitters [4]. Another technique that we have been exploring is to investigate scintillation characteristics of different beams and transmit the one that has the best immunity to turbulence. In order to do that, scintillation of different beam types is formulated and evaluated. By scintillation, we refer to the fluctuations of power by a photodetector after the optical wave has propagated through a turbulent medium. The first studies on laser beam scintillations are those by Schmeltzer [5] and Ishimaru [6]. Scintillation together with beam wander has been the most prominent factor for light detection. Scintillation effects for horizontal paths have been analyzed and formulated for different types of beams [7, 8]. Lately, there also appeared practical applications using different beam types to improve the modulation efficiency of optical links [9]. Among these, Laguerre-Gaussian (LG) beams are of special interest, because they are easily realized by various methods [10, 11]. In previous studies, scintillation calculations of partially coherent LG [12] and fully coherent LG beams [13] are presented for horizontal paths.

Both theoretical studies and measurements are made to analyze the temperature effect and ground wind velocity effect on the scintillation and bit error rate of various beam types [14–16]. It is found in [17, 18] that uplink and downlink scintillation effects differ significantly. In this sense, the beam width remains smaller than the outer scale of the turbulence during the uplink, and the beam may leave the atmosphere with a significant change in direction [17, 18]. The downlink beam, however, arrives at the atmosphere with a width much larger than any turbulent eddy; hence, uplink scintillation has been demonstrated to be more dominant over downlink for various beam types [17–20]. Consequently, here we have chosen to study the uplink scintillation. The atmospheric air mass that is traversed in a typical ground satellite slant path is equivalent to that encountered in a few hundred meters long horizontal ground level path. Hence along slant paths, weak scintillation conditions, consequently Rytov approximation, are applicable. LG beam slant path propagation has not been analyzed up to now. In this study, slant path propagation of LG beam is investigated, and scintillation indices of the LG beams are given for on- and off-axis receiver points. Section 2 describes the formulation regarding the Rytov approximation for a slant link. In Sect. 3, numerical results are presented to compare the scintillation index for different cases of slant links, and in Sect. 4, concluding remarks are given.

2 Formulation

In Rytov solution, scintillation index, b 2 is retrieved from [21];

$$ b^{2} = 2E_{2} ( {p,R}) + 2\,{\text{Re}}\left[ {E_{3} ({p,R})} \right] $$
(1)

where \( E_{2} ({}) \) and \( E_{3} ({}) \) are integrals related to the averages of first order complex phase perturbation. p is the radial coordinate on the transverse receiver plane, R is the distance between the source and the receiver.

By omitting the angular dependence, LG beam formulation on the source plane [13] becomes

$$ u_{s} (s) = \left( { - j\sqrt {2s/\alpha_{s}^{2} } } \right)^{l} \exp \left( { - s^{2} /\alpha_{s}^{2} } \right)L_{m}^{l} \left( {2s^{2} /\alpha_{s}^{2} } \right) $$
(2)

where s is radial coordinate of the source plane, j is the complex number \( \sqrt { - 1} \), α s is the Gaussian source size, \( L_{m}^{\;l} \left( {} \right) \) indicates the associated Laguerre polynomial with m and l corresponding to radial and angular mode numbers, respectively. In this study, Kolmogorov spectrum function is selected, which is

$$ \Upphi_{n} \left( \kappa \right) = 0.033\kappa^{ - 11/3} \bar{C}_{n}^{2} $$
(3)

where is κ refers to the spatial frequency variable. For a fixed altitude of H, the altitude dependent average structure constant, \( \bar{C}_{n}^{2} \) of the slant path is given by

$$ \bar{C}_{n}^{2} = \frac{1}{H}\int\limits_{0}^{H} {C_{n}^{2} (h){\text{d}}h} $$
(4)

According to the well-known Hufnagel-Valley model [22] the altitude-dependent structure function, \( C_{n}^{2} \left( h \right) \) can be expressed as

$$ C_{n}^{2} \left( h \right) = 8.148 \times 10^{ - 56} V^{2} h^{10} \exp \left( { - h/1,000} \right) + 2.7 \times 10^{ - 16} \exp \left( { - h/1,500} \right) + C_{0} \exp \left( { - h/100} \right) $$
(5)

As a typical nominal value at ground level C 0 is taken to be \( 1.7 \times 10^{ - 15} \,{\text{m}}^{2/3} \) and wind speed along the slant path, V is computed from [23]

$$ V = (v_{g}^{2} + 30.69v_{g} + 348.91)^{1/2} $$
(6)

where v g is the ground wind speed which is set to zero for convenience in this paper. Altitude and distance parameters are simply related as

$$ H = R\,\cos \zeta $$
(7)

where ζ is the zenith angle. Equation (7) also implies

$$ h = \chi \,\cos \zeta $$
(8)

where χ is the distance variable. Equation (5) is integrated according to (4) and its well-approximated version is inserted into the final scintillation index expression.

Benefiting from the earlier derivations [8, 13, 24, 25], \( E_{2} \left( {} \right) \) and \( E_{3} \left( {} \right) \) in (1) can be evaluated for the LG source given in (2) and the spectrum model given in (3), then taking into account the dependence of the structure on altitude as expressed in (4) and (5), the scintillation index is yielded as

$$ \begin{aligned} b^{2} (p,R) = & \frac{{0.4147(2\pi /\lambda )^{2 - 2l} }}{{p^{2l} \left[ {L_{m}^{l} \left( {\frac{{2\pi^{2} \alpha_{s}^{2} p^{2} }}{{\pi^{2} \alpha_{s}^{4} + \lambda^{2} R^{2} }}} \right)} \right]^{2} }}\int\limits_{0}^{R} {\int\limits_{0}^{\infty } {\int\limits_{0}^{2\pi } {\hbox{d}\chi \kappa \hbox{d}\kappa \hbox{d}\theta_{\kappa } } } } \kappa^{ - 11/3} \left\{ {4.05 \times 10^{ - 13} } \right.\left[ {1 - \exp \left( { - \chi \cos \zeta /1,500} \right)} \right] \\ & \left. { + 100C_{0} \left[ {1 - \exp \left( { - \chi \cos \zeta /100} \right)} \right]} \right\}/\left( {\chi \cos \zeta } \right) \\ & \times \left( {\left[ {\kappa^{2} \left( {R - \chi } \right)^{2} - \frac{4\pi }{\lambda }\kappa p\left( {R - \chi } \right)\cos \theta_{\kappa } + \frac{{4\pi^{2} p^{2} }}{{\lambda^{2} }}} \right]^{l} \left[ {\frac{{2\lambda \left( {R^{2} + \chi^{2} } \right) + \pi^{2} \alpha_{s}^{4} }}{4}} \right.} \right. \\ & \left. { + \frac{{R^{2} \chi^{2} \lambda^{4} }}{{4\pi^{2} \alpha_{s}^{4} \left( {\pi \alpha_{s}^{2} + \lambda } \right)^{4} R^{2} \chi^{2} }}} \right]^{m} \exp \left[ {\frac{{4\pi \lambda \alpha_{s}^{6} \kappa p\left( {R - \chi } \right)\cos \theta_{\kappa } - \pi^{2} \lambda^{2} \alpha_{s}^{4} \kappa^{2} \left( {R - \chi } \right)^{4} }}{{2\pi R^{2} \left( {\pi^{2} \alpha_{s}^{4} + \lambda^{2} } \right)}}} \right] \\ & \times \left. {\left| {L_{m}^{l} \left[ {\frac{{j\lambda^{2} \alpha_{s}^{2} \left( {\pi \alpha_{s}^{2} + j\lambda \chi } \right)}}{{2\left( {\pi \alpha_{s}^{2} + j\lambda R} \right)}}\frac{{\kappa^{2} \left( {R - \chi } \right)^{2} - \frac{4\pi }{\lambda }\kappa p\left( {R - \chi } \right)\cos \theta_{\kappa } + \frac{{4\pi^{2} p^{2} }}{{\lambda^{2} }}}}{{\pi \lambda \alpha_{s}^{2} \left( {R - \chi } \right) + j\left( {\pi^{2} \alpha_{s}^{4} + \lambda^{2} R\chi } \right)}}} \right]} \right.} \right|^{2} \\ & + {\text{Re}} \left\{ {\left( { - 1} \right)^{m + 1} \left[ { - \kappa^{2} \left( {R - \chi } \right)^{2} \exp \left( {2j\theta_{\kappa } } \right) + \frac{{4\pi^{2} p^{2} }}{{\lambda^{2} }}\left( {\frac{{\pi \alpha_{s}^{2} - j\lambda \chi }}{{\pi \alpha_{s}^{2} - j\lambda R}}} \right)^{2m} } \right]} \right.^{l} \\ & \times \left[ {\frac{{\pi \lambda \alpha_{s}^{2} \left( {R - \chi } \right)}}{{2\left( {\lambda^{2} + \pi \alpha_{s}^{2} } \right)\chi^{2} }}} \right. + \left. {\frac{jR}{2\chi }} \right]^{2m} \exp \left[ { - j\kappa^{2} \lambda \left( {R - \chi } \right)\frac{{\pi \alpha_{s}^{2} + j\lambda \chi }}{{\pi \alpha_{s}^{2} + j\lambda R}}} \right] \\ & \times L_{m}^{l} \left[ {\frac{{j\lambda^{2} \alpha_{s}^{2} \left( {\pi \alpha_{s}^{2} + j\lambda \chi } \right)}}{{2\left( {\pi \alpha_{s}^{2} + j\lambda R} \right)}}\frac{{\kappa^{2} \left( {R - \chi } \right)^{2} - \frac{4\pi }{\lambda }\kappa p\left( {R - \chi } \right)\cos \theta_{\kappa } + \frac{{4\pi^{2} p^{2} }}{{\lambda^{2} }}}}{{\pi \lambda \alpha_{s}^{2} \left( {R - \chi } \right) + j\left( {\pi^{2} \alpha_{s}^{4} } \right. + \left. {\lambda^{2} R\chi } \right)}}} \right] \\ & \left. {\left. { \times L_{m}^{l} \left[ {\frac{{j\lambda^{2} \alpha_{s}^{2} \left( {\pi \alpha_{s}^{2} + j\lambda \chi } \right)}}{{2\left( {\pi \alpha_{s}^{2} + j\lambda R} \right)}}\frac{{\kappa^{2} \left( {R - \chi } \right)^{2} + \frac{4\pi }{\lambda }\kappa p\left( {R - \chi } \right)\cos \theta_{\kappa } + \frac{{4\pi^{2} p^{2} }}{{\lambda^{2} }}}}{{\pi \lambda \alpha_{s}^{2} \left( {R - \chi } \right) + j\left( {\pi^{2} \alpha_{s}^{4} + \lambda^{2} R\chi } \right)}}} \right]} \right\}} \right) \\ \end{aligned} $$
(9)

3 Results and discussion

Results are obtained numerically by computing the triple integral in (9) via the routine described in [8]. λ = 1.55 × 10−6 m is used for wavelength and scintillation index dependence on propagation distance, source size, and radial distance at the receiver plane are displayed for zenith angles ζ = 10°, 15°, 30°, 40°, 75°.

For the on-axis positions, i.e., at p = 0, angular mode number l ≠ 0 will lead to undefined scintillation index values [13], as also apparent from (9). For this reason, on-axis calculations can only be made for l = 0.

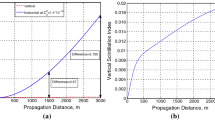
Figures 1 and 2 show the on-axis scintillation index variation with propagation altitude at angular mode number l = 0 and ζ = 15° and 75°. From Figs. 1 and 2, it is seen that, the scintillation index gets lower as the radial mode number increases, but in general, the scintillation index for the ζ = 15° is lower than that of ζ = 75° which means that, as the link becomes more vertical, the scintillation will inevitably decrease. In Figs. 1 and 2, the solid lines, i.e., m = 0, l = 0, correspond to the fundamental Gaussian beam. This way, all LG beams have lower scintillation than Gaussian beam, but radial mode numbers beyond m = 5 start to bring less and less scintillation reductions. Figure 3 displays the off-axis scintillation index for angular mode l = 1 on a link of ζ = 75°. Here Gaussian source size is changed to α s  = 2 cm and off-axis radial point of p = 2 cm is chosen. When compared with Fig. 2, Fig. 3 shows that angular mode number of one creates substantially higher scintillations. On the other hand, Fig. 3 reveals that it is possible to lower scintillation by increasing radial mode number just like in Figs. 1 and 2. We should also note that, in all the cases examined so far, the separation between the curves becomes larger with increases in propagation altitudes.

Fig. 1
figure 1

On-axis scintillation index variation with propagation altitude for several m values with l = 0 and ζ = 15°

Full size image
Fig. 2
figure 2

On-axis scintillation index variation with propagation altitude for several m values with l = 0 and ζ = 75°

Full size image
Fig. 3
figure 3

Off-axis scintillation index variation with propagation altitude for several m values with l = 1 and ζ = 10°

Full size image

Figures 4 and 5 provide the display of the on-axis scintillation index dependency on source size at propagation altitudes of 30 and 10 km, for ζ = 75° and ζ = 30°. H = 30 km altitude corresponds to a typical high-altitude surveillance platform application. For ζ = 75°, the altitude is confined to H = 10 km for the Rytov approximation to be valid. After this point, strong turbulence approximation formulation has to be applied. In Figs. 4 and 5, the behavior of the scintillation index appears to be similar to that of Figs. 1, 2, that is, less scintillation obtained at higher radial mode numbers and at smaller zenith angles. As before the fundamental Gaussian beam with m = 0, l = 0 has the highest scintillation in both Figs. 4 and 5. However, the separation between the different scintillation curves is slightly increased at bigger source sizes. Furthermore, there seems to be a dip in scintillations around middle source sizes.

Fig. 4
figure 4

On-axis scintillation index variation with source size for several m values with l = 0 and ζ = 30°

Full size image
Fig. 5
figure 5

On-axis scintillation index variation with source size for several m values with l = 0 and ζ = 75°

Full size image

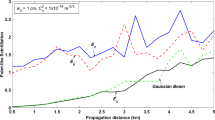
Figures 6, 7, and 8 display the variation of scintillation index with the off-axis points on receiver plane. By comparing Figs. 7 and 8, we observe that the previously detected fact that the more slant paths, i.e., the larger values of ζ introducing more scintillation continues to be valid here as well. In Fig. 6, all LG beams, including the fundamental Gaussian beam, have almost constant scintillation index for the off-axis points considered, but the rise of scintillations for LG beams seem to be getting steeper particularly with rising radial mode number. When the angular mode number is different than zero, however, as is the case in Figs. 7 and 8, the trend changes, and scintillations begin to decrease with increasing off-axis distance for smaller radial mode numbers but the reverse happens for larger radial mode numbers. In addition to the off-axis case, as we move more toward the edges of the received beam, the scintillation differences between the beams of smaller radial mode numbers are gradually reduced.

Fig. 6
figure 6

Off-axis scintillation index variation with radial distance for several m values with l = 0 and ζ = 30°

Full size image
Fig. 7
figure 7

Off-axis scintillation index variation with radial distance for several m values with l = 1 and ζ = 30°

Full size image
Fig. 8
figure 8

Off-axis scintillation index variation with radial distance for several m values with l = 1 and ζ = 40°

Full size image

4 Conclusion

Scintillations of the Laguerre-Gaussian beams for vertical links of various zenith angles are formulated and computed. Rytov approximation is used to find the scintillation index. Numerical results are given to demonstrate the effect of slant propagation length, off-axis receiver point, and source size on the scintillation. Also different radial and angular mode numbers for the LG beams are investigated to show their effects on scintillation. As the uplink beam is inclined more toward horizontal plane and at higher angular mode numbers, scintillations are increased. However, increasing radial order number helps to decrease the scintillation both at on-axis and off-axis positions and at all source sizes. Furthermore, LG beams of zeroth order angular mode is mostly found to be advantageous as compared to fundamental Gaussian beam. In this respect, the use of LG beams may be preferred for optical communication links.