Transmission Bragg-grating grisms for pulse compression

Abstract

We design a grism compressor based on transmission gratings and high refractive index prisms to compensate for both the second- and third-order dispersions of SF57 glass at 800 nm. The use of transmission gratings eases the geometrical constraints, allows a final recombination of the spectral components out of the bulk of the prisms and suggests a potential application of these grims to high-energy pulse compression. The dispersion law of this grism compressor is measured in double-pass configuration and negative third-order dispersion is achieved. We demonstrate efficient operation with an overall throughput >60% over a 100 nm bandwidth.

1 Introduction

Chirped-pulse amplification (CPA) requires optical devices characterized by large group delay dispersions (GDD) to stretch/compress the ultrashort pulses before/after the amplification stage. In the first embodiment of CPA [1] in 1985, the laser pulses were stretched in a fused silica fiber with positive GDD and compressed by a pair of reflective gratings arranged to provide negative GDD (Treacy configuration [2, 3]). However, as both fused silica and grating pairs introduce a high level of positive third-order dispersion (TOD) in the near infrared, the dispersion of the grating pair was not perfectly opposite to the dispersion of the fiber [4] and the pulses could not be recompressed to their Fourier-transform limit. To solve this issue and achieve a perfect matching between stretcher and compressor, an open-space stretcher combining reflective gratings and an imaging afocal telescope of magnification -1, introduced by Martinez [5] in 1987, can be used. Since then, Treacy compressors and Martinez/Öffner stretchers [6] have been extensively used in CPA laser systems.

The use of bulk stretchers made of highly dispersive glass rods simplifies the overall design of CPA sources and improves their long-term stability. These devices are indeed immune to vibrations, mechanical or thermal drifts and offer the highest throughput and bandwidth. If grating-based stretchers have been favored in the earlier years of CPA because of their larger GDD, the recent spread of ultrabroadband sources (>50–100 nm) brings a renewed attention to bulk stretchers and to the issue of TOD compensation. In 1969 [7], it was already pointed that TOD could be canceled or inversed by replacing reflective gratings by a combination of gratings and prisms [8].

However, these very first grisms were designed far from the Littrow incidence and suffered from low diffraction efficiency. Besides, the highest peak power was reached in the bulk of the prisms which induced a high level of non-linear effects such as self-focusing and self-phase-modulation. In practice, these drawbacks prevented the practical use of these grisms as pulse compressors. Since then several other grism designs based on reflective gratings have been proposed and demonstrated [9–13]. By working closer to the Littrow angle, the diffraction efficiency of the gratings could be enhanced to that of conventional grating compressors [14]. Yet, the issue of nonlinear effects was not solved, which limited the applications of grisms to low-energy pulse compression in up-chirped CPAs [15] or pulse stretching in down-chirped CPAs [9]. Although out of the scope of this paper, grisms have also found applications in research fields such as pulse-shaping devices [16, 17], achromatic phase-matching schemes in nonlinear optics [18], confocal microscopy [19] or nonlinear endomicroscopy [20].

In this letter, we study a grism compressor comprising two parallel Bragg gratings between which two anti-parallel, right-angle, high-index prisms are placed (Fig. 1). As opposed to designs based on reflective gratings, the use of transmission gratings simplifies the geometrical constraints and allows to work at the exact Littrow angle, where the diffraction efficiency and bandwidth are optimal. With this geometry, the distance between the optical components can also be varied arbitrarily and the resulting GDD and TOD can be continuously tuned from 0 to a value only bounded by the transverse dimension of the optics. Last, an air gap can be introduced between the first grating and the first prism, which enables a final recombination of the spectral components out of the bulk of the prisms. This key feature could considerably reduce the level of nonlinear effects and suggest a potential application of these grisms to high-energy pulse compression. As a proof of concept, we experimentally characterize a grism compressor designed to compensate for both the GDD and TOD of an SF57 glass rod at 800 nm.

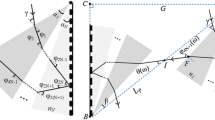
2 Principle

Fig. 1

Single-pass grism setup

Let $\sigma$ be the groove density of the gratings and $\alpha$ be the apex angle of the prisms of refractive index $n.$ The prisms are inserted between the gratings with the outer faces parallel to the grating surfaces. Let $L$ be the distance between the outer faces of the prisms, $G=G_1+G_2$ be the total air gap between the grating and the prisms, $H$ be the perpendicular distance between the prism apices, measured as the projection of the segment linking the apices along the grating surface. The distance between the inner surfaces of the prisms is $d=L\cos (\alpha )-H\sin (\alpha )$. The total length of the device is $G+L$. Light propagates from left to right and the input beam direction is $\theta _i$ with respect to the normal to the grating surfaces. The first Bragg order is diffracted in air with a positive angle $\theta _d$ given by the grating rule:

$$\begin{aligned} \sin (\theta _d)-\sin (\theta _i)=c\frac{\sigma }{\nu } \end{aligned}$$

(1)

where $\nu$ is the optical frequency and $c$ is the velocity of light in vacuum. The diffracted beam is then refracted by the first air–glass interface and propagates in glass with an angle $r_1$ with respect to the input face. Let $r_2$ be the incidence angle at the output glass–air interface and $i_2$ be the propagation direction in air after the second refraction with respect to the normal to the glass–air surface. The angles $\theta _d$, $r_1$, $r_2$, $i_2$ and $\alpha$ are linked by

$$ \left\{ \begin{array}{l} n\sin (r_1)=\sin (\theta _d)\\ r_2=r_1-\alpha \\ n\sin (r_2)=\sin (i_2) \end{array} \right. $$

(2)

The beam travels in air the distance $d/\cos (i_2)$, is refracted by the second prism, diffracted by the second grating and exits parallel to the input beam direction. We now consider the total group delay $\tau _p$ added by the grism pair to a plane wave propagating between the reference planes defined by the two prisms apices and the direction $\theta _i$. Let $N$ be the group delay index of the prisms. All interfaces being two-by-two parallel, it is clear that the total group delay depends neither on the incident position of the input beam nor on the repartition of the air gaps between the gratings and the prisms. For the sake of simplicity, it is therefore convenient to assume, without any loss of generality, that the first grating is engraved on the first prism and that the input light ray hits the first prism at the apex. The absolute group delay $\tau _p$ is then equal to the sum of the group delays of the three consecutive propagating segments, in air ($d$), glass (second prism) and air again:

$$\begin{aligned} c. \tau _p&= \frac{d}{\cos (i_2)}+\frac{L}{\cos (r_1)}\left[ N-\sin (\theta _i)\frac{\cos (r_2)}{\sin (\alpha )} \right] \nonumber \\ &\quad\times \left[ 1-\frac{d}{L} \frac{\cos (\alpha +i_2)}{cos(i_2)} \right] +G\frac{1-\cos (\theta _i-\theta _d)}{\cos (\theta _d)} \end{aligned}$$

(3)

It is easy to check that these three terms are always positive, as can be expected for absolute group delays. As can be shown by numerical investigation, the total third-order dispersion of a grism pair becomes negative when $r_2$ is close to the critical angle for total internal reflection. As a general trend, for given $G$, $H$ and $L$ values, large apex angles correspond to negative TOD, whereas small apex angles correspond to positive TOD. From a design point of view, once the groove density and the optical indices have been defined, the dispersion law of the grism compressor depends on five independent geometrical variables. However, since $\theta _i$ has to be equal to the Bragg incidence ($2\sin \theta _i=-c\sigma /\nu _0$) there remains, in fact, only four independent geometrical parameters: the apex angle $\alpha$, the geometrical parameters $g=G/L$, $h=H/L$ and the scaling length $L$. It is also worth noting that the contribution of the air gap $G$ (last term of Eq. 3) to the total dispersion is minor when compared with the other terms and that negative TOD values can also be reached if $G=0$. As for pairs of prisms or gratings, a pair of grism exhibits in single pass a lateral chromatism since all the optical rays exit the grism pair with the same direction but at frequency-dependent location. In the experiments described below, a roof-top mirror was used to double-pass the grism pair and compensate for this effect.

Fig. 2

Theoretical group delay in double-pass configuration as a function of frequency computed from Eq. (solid line) and from a ray tracing algorithm (dots). Inset: ray tracing plot showing the optical propagation at 750 and 850 nm. Units are cm

3 Experimental results

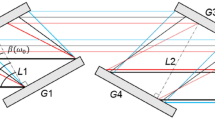
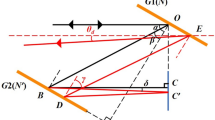
A grism compressor was assembled from 10 $\times$ 20 mm$^2$ fused-silica gratings with a groove density of 1,250 g/mm (Ibsen Photonics, damage threshold >40 GW/cm$^2$ http://www.ibsen.dk/highpower) and 25 $\times$ 25 mm$^2$ SF57 prisms with a apex angle of 42.5$^\circ$. Broadband anti-reflection coatings were deposited on the substrate sides of the gratings as well as on the three facets of the prisms. The apex angle $\alpha$ = 42.5$^\circ$ and the geometrical parameters $g$ = 0.32 and $h$ = 0.8 were chosen. For practical reasons, the selected geometrical parameters were $G\simeq$ 10 mm, $H\simeq$ 25 mm and $L\simeq$ 31 mm. The dispersion law of the corresponding compressor in double-pass configuration is shown in Fig. 2 together with a sketch of the compressor. the The total size of the compressor was 25 $\times$ 40 mm$^2$, which is a little smaller than a grating compressor with the same GDD. The dispersion law of the grism pair was measured, in double-pass configuration, by spectral interferometry: the grism compressor was inserted in one arm of a dispersion balanced Michelson interferometer and the interference pattern was recorded with a spectrometer (AvaSpec2048L from Avantes, spectral resolution of 0.1 nm). However, given the large dispersion of the grism compressor and the finite resolution of the spectrometer, it was not possible to resolve the interference pattern over the complete spectral range. Rather than retrieving the spectral phase piecewise, we measured directly the group delay as a function of frequency, using the method described by  [9]: due to the high dispersion of the grisms, the interferogram exhibits chirped fringes with a flat fringe localized at the wavelength for which the group delay is equal on both arms (Fig. 3). By varying the length of the reference arm and recording the coincidence wavelength, the group delay of the grism compressor could be retrieved with $\pm$60 fs and $\pm$0.3 THz accuracies over the full bandwidth of a $\simeq$12 fs mode-locked oscillator (740–840 nm).

Fig. 3

Example of experimental interference pattern (solid line) between the input spectrum (dots), the output of the grism compressor (dashed line)

Fig. 4

Group delay as a function of frequency for three settings. Blue dots: experimental points. Blue solid line: parabolic fit. Red dashed line: linear fit

A polynomial fit of the group delay as a function of angular frequency was then used to extract the GDD and TOD values. As shown in Fig. 4, for the experimental parameters $G1+G2\simeq 8$ mm, $H\simeq 25$ mm, $L\simeq 31$ mm and $\theta _i\simeq -32.5^\circ$ the measured GDD and TOD were equal to $-$1.62 $\times$ 10$^5$ fs$^2$ and $-$0.94 $\times \,$10$^5$ fs$^3$, in good agreement with the theoretical values ($-$1.64 $\times$ 10$^5$ fs$^2$ and $-$0.91 $\times$ 10$^5$ fs$^3$) given the fit accuracy ($\pm$0.03 $\times$ 10$^5$ fs$^2$ and $\pm$0.18 $\times$ 10$^5$ fs$^3$). The corresponding experimental TOD/GDD ratio was comprised between +0.47 and +0.69 fs and the corresponding chirp ratio was of $\simeq$0.5 ps/nm. Although not demonstrated here, such GDD values would be large enough to compensate for the dispersion of an SF57 rod of approximately 73 cm. By translating one of the prism parallel to the gratings it was possible to vary the TOD/GDD ratio from $-$0.5 fs to +0.7 fs, encompassing the value of +0.63 fs necessary to compensate for the TOD/GDD ratio of SF57. As shown in Fig. 4, the curvature of the group delay as a function of frequency decreases from positive to negative as $H$ is decreased. For $H\simeq$28 mm, the TOD nearly vanishes and the dispersion of the grims compressor is almost completely linear with frequency.

Fig. 5

Transmission of the double-pass grism compressor as function of wavelength. Blue dash-doted line: normalized input spectrum. Solid dark line: output spectrum. Red dots: transmission

The total throughput of the grism compressor was $\simeq 65\%$ at 800 nm, >60 % over the 740–840 nm bandwidth and >50 % over the 710–875 nm bandwidth (Fig. 5). As it can be noticed, the latter bandwidth ($\simeq$165 nm at 790 nm) is large enough to sustain Gaussian pulses of $\simeq$12 fs FWHM. Assuming a perfect compression at the output of the grism compressor, the group delay function at the output of the last prism (first prism in double-pass configuration) is given by the last term of Eq. 3 for $G\,=\,G1$. For the experimental parameters, the calculated group delay spreads from $-$2.0 to +2.9 ps over the 700–900 nm bandwidth and indicates that for $\simeq$12 fs pulses, the shortest pulse duration in the bulk of the prism would be about 1.8 ps FWHM (Fig. 6). With $G1=8$ mm and $G2=0$, this value could even reach 3.6 ps FWHM.

Fig. 6

Calculated group delay added by the last air interval

4 Conclusion

Grism compressors based on Bragg transmission gratings and high refractive index prisms open the path to efficient and broadband compression scheme with adjustable third-order dispersion phase. Such compressors could be designed to match and compensate for the GDD and TOD of bulk stretchers, with chirp ratii large enough to sustain $<$15 fs, mJ-level, amplified pulses.