Electronic detection of a single particle in a coplanar-waveguide Penning trap

Abstract

We present a detailed model of the electronic detection of a single particle in a coplanar-waveguide Penning trap. The detection signal is the electric current induced upon the trap’s surface by the charged particle’s motion. In contrast to three-dimensional hyperbolic or cylindrical traps, the cyclotron and magnetron motions can be detected, excited or coupled to the axial motion without segmenting any of the trap’s electrodes. We calculate the effective coupling displacement for different electrodes. This determines the detection signal and resistive cooling time constant for each component of the ion’s motion. We discuss the practical implementation of the electronic detection for a single electron and a single proton.

1 Introduction

Several types of planar Penning traps have been proposed [1–3]. One of the original motivations for the development of those traps has been the possibility of implementing an scalable quantum processor with trapped electrons [4] or laser cooled ions [5, 6]. In our lab, we particularly focus on electrons. Besides quantum computation, electrons in planar Penning traps have also applications in quantum metrology [7], quantum simulation of magnetism [8] and matter–wave interferometry [9]. The trap presented in [1] has been tested experimentally with a cloud of electrons, at room temperature [10] and with a cryogenic set-up [11]. However, the observation of a single electron in a planar Penning trap and the measurement of its motional frequencies, with accuracy similar to that of 3D traps, is an open experimental challenge [11].

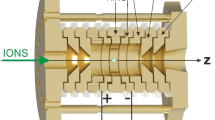
A novel planar Penning trap has been recently proposed at the University of Sussex [12]. It basically consists of a section of a coplanar-waveguide [13], therefore the name coplanar-waveguide Penning trap (CPW-trap). Its sketch is shown in Fig. 1. The CPW-trap emerges from the projection of the well-known cylindrical Penning trap onto a flat surface. This results in the preservation of the axial symmetry of the latter and allows for the accurate measurement of the particle’s motional frequencies [12]. The design of the trap has been also inspired by superconducting coplanar-waveguide resonators, such as those used in circuit-QED experiments [14, 15]. Different trapping technologies for different atomic species have been considered to be integrated within superconducting circuits, such as Bose–Einstein condensates in atom chips [16], polar molecules [17] and molecular ions in RF-traps [18]. Besides quantum computation, the coplanar-waveguide Penning trap has also potential applications in FT-ICR mass spectrometry and in the study of metallic surfaces with trapped electrons/ions as magnetic sensors. These are being investigated in our group and will be reported in future publications.

Fig. 1

Coplanar-waveguide Penning trap. The picture illustrates the cyclotron and axial motions of a trapped particle (see Sect. 2.1.1). The trap is patterned onto a metallic chip on a dielectric substrate. The area beyond the electrodes (not shown) is supposed to be dc-grounded

In this article, we present a theoretical model of the electronic detection of a single electron/ion in a CPW-trap. The electronic detection of charged particles in a Penning trap was first introduced by H. Dehmelt [19]. The particle induces a current upon the trap’s metallic surface. This is picked-up by a resonant parallel LC-circuit. The resulting voltage is amplified and observed in the frequency domain [20]. This allows for the measurement of the particle’s motional frequencies with very high accuracy (see, for instance, [21]). The detection of the spin state relies also on those frequency measurements [22]. Thus, the implementation of the electronic detection system is essential, particularly when the trap is used to confine electrons, protons, or any other species with no optical transitions available for their observation.

2 The coplanar-waveguide Penning trap

As shown in Fig. 1, in its basic configuration the CPW-trap consists of five rectangular electrodes. These are: the “ring”, two compensation (or correction) electrodes and two end-caps. Two “ground-planes”—flanking the central electrodes—are also necessary, for shielding the substrate and for a well defined dc-ground reference. The magnetic field is parallel to the surface of the chip, $\mathbf{B}=B\cdot\hat{u}_{z}$. The electrodes’ dimensions and the applied voltages are given in Fig. 2. The ring, compensation and end-cap voltages are denoted by V _r ,V _c and V _e , respectively. The symbols l _i represent the different electrodes’ lengths, while S ₀ represents their width and η the small insulating gap between any of them. Other important symbols are the tuning ratio, T _c =V _c /V _r , and the end-cap to ring ratio, T _e =V _e /V _r .

Fig. 2

Sketch of the CPW-Penning trap. The coordinates’ origin, (0,0,0), is at the centre of the ring-electrode

2.1 Basic characteristics

The electrostatics of the CPW-Penning trap can be calculated analytically [12], as well as the microwave propagation modes [23], and other high-frequency properties [24]. The working characteristics of this Penning trap are discussed in detail in [12]. Here, we present a summary of its main features.

Figure 3 shows a plot of the equipotential lines for a typical voltage configuration: with |V _e |>|V _r | and V _c ≃V _e . Negative voltages are assumed, thus allowing for the capture of electrons or any negatively charged ions. The equilibrium position, (0,y ₀,0), is located at the centre of the quadrupole field, where the electrostatic force upon the trapped particle vanishes. The trapping height, y ₀, is mainly a function of the end-cap to ring ratio, T _e , with a small dependence on the tuning ratio, T _c [12]. The latter is used for compensating linear anharmonicities of the trapping potential [12].

Fig. 3

Plot of the equipotential surfaces and electric field of the CPW-Penning trap. Around the equilibrium position the field has the form of a quadrupole electric field

2.1.1 The ideal CPW-Penning trap

Around the equilibrium position, the ideal quadrupolar trapping potential is given by [12]:

$$ \phi_{\mathrm{quad}}=V_r\,c_{002} \biggl(z^2- \frac{x^2+(y-y_0)^2}{2}+\frac {\epsilon}{2}\bigl(x^2-(y-y_0)^2 \bigr) \biggr). $$

(1)

c ₀₀₂ represents the curvature along the $\hat{u}_{z}$-axes of the electrostatic potential (see Fig. 3). The ellipticity parameter is $\epsilon=\frac{c_{200}-c_{020}}{c_{002}}$, where we have introduced the curvatures along $\hat{u}_{y}\leftrightarrow c_{020}$ and $\hat{u}_{x}\leftrightarrow c_{200}$. The asymmetry between the two radial directions $\hat{u}_{y}$ and $\hat{u}_{x}$ implies that, in general, ϵ is not vanishing, i.e. the CPW-trap is an elliptical Penning trap [25, 26]. Analytical expressions for the reduced cyclotron (ω _p =2πν _p ), magnetron (ω _m =2πν _m ) and axial (ω _z =2πν _z ) frequencies in an ideal elliptical Penning trap are derived in [25]. Furthermore, the motion of the particle around (0,y ₀,0) is governed by the equations:

(2)

The explicit expressions of the coefficients ξ _p,m and η _p,m can be found in [25]. The amplitudes, A _p ,A _m and A _z are given in [12]. The ideal motion of the particle around (0,y ₀,0) is plotted in Fig. 4. In this example, the ellipticity is positive, ϵ>0. In the opposite case, ϵ<0, the major axes of the radial (magnetron) ellipse aligns itself along $\hat{u}_{y}$. In general, the applied voltages, V _r ,V _c ,V _e , must be chosen such that the condition −1<ϵ<1 is fulfilled, otherwise trapping is not possible [25].

Fig. 4

Motion of a particle in a CPW-Penning trap. The radial motion, (x(t),y(t)−y ₀), follows an elliptical orbit

2.1.2 Useful trapping interval

Anharmonic deviations of the real potential from the ideal case of Eq. (1) result in fluctuations of ω _p ,ω _z and ω _m with the particle’s energies. The biggest fluctuations are caused by second order anharmonicities [12]. These can be cancelled by applying an appropriate optimal tuning ratio, $T_{c}^{\mathrm{opt}}$. However, $T_{c}^{\mathrm{opt}}$ can be found only within a limited (continuous) interval of trapping heights y ₀ [12]. Outside that useful trapping interval the dependence of the frequencies with the energies make the electronic detection of a single particle extremely difficult or even impossible. The useful trapping interval depends on the particular CPW-trap and is solely defined by its dimensions [12]. Within that interval the particle can be detected and ω _p ,ω _z ,ω _m can be measured accurately. However, the electronic detection signal strongly depends on y ₀. This is discussed in detail in Sect. 4.

3 Electronic detection of the particle’s motion

The principle of the electronic detection technique is illustrated in Fig. 5. The particle induces a charge density on the trap’s surface. A parallel tank circuit, (with L=inductance, C=capacitance and losses modelled by the resistance R) is connected to one of the trap’s electrodes, thus allowing the induced charges to “escape” to ground. In the example, the electrode is capacitively coupled to the LC-circuit, thereby blocking the applied dc-voltage from earth. The coupling might be also inductive (see, for instance, [27]). The induced current, I _ind(t), generates a voltage signal across the LC-circuit, V _ind(t). This can be amplified and then observed in the frequency domain. The voltage is proportional to both the induced current and the impedance of the LC-circuit: V _ind=I _ind⋅Z(ω). The circuit is therefore usually tuned to maximise Z(ω) at the motional frequency of the particle. This is the case when its resonance frequency, $\omega_{LC}=1/\sqrt{LC}$, equals the particle’s eigenfrequency.

Fig. 5

Detection of the axial motion. A trapped electron induces positive charges upon one of the correction electrodes. For simplicity the ground-planes have been omitted

3.1 Calculation of the induced current

In the first place, the charge induced upon the electrodes must be obtained. It can be calculated by means of the Green’s function for Laplace’s equation with Dirichlet’s boundary conditions, G(r|r′), [28]:

(3)

In Eq. (3), the surface integral extends over the surface Σ of the particular electrode chosen for picking-up the induced current. The “source coordinate” is represented by r′∈Σ, while the position of the trapped particle at time t is given by r(t). Assuming that the conducting chip that houses the trap is an infinite plane (y=0), the appropriate Green’s function is [28]:

(4)

The particle’s motion, r=r(t), generates the induced current: $I_{\mathrm{ind}}(t)=\frac{d q_{\mathrm{ind}}(\mathbf{r}(t))}{dt}$. This can be expressed as

(5)

3.2 Resistive cooling of the motion

The induced voltage, V _ind, generates an electric potential which acts upon the trapped particle itself. This “self-induced” potential can be calculated by means of Eq. (4) and using Green’s second identity [28]:

(6)

In Eq. (6), the induced voltage is constant over Σ and can be extracted from the integral. According to Eqs. (3) and (5), we have

$$ \phi_\mathrm{ind}=-V_\mathrm{ind}\cdot\varLambda_{\varSigma}( \mathbf{r})=q Z(\omega )\varLambda_{\varSigma}(\mathbf{r})\boldsymbol{\nabla} \varLambda_{\varSigma}(\mathbf{r})\cdot \dot{\mathbf{r}}. $$

(7)

ϕ _ind generates an electric field which, in turn, creates a force upon the trapped particle: $\mathbf{F}_{\mathrm{ind}}=-q\cdot\boldsymbol{\nabla} \phi_{\mathrm{ind}}=-q^{2} Z(\omega)\cdot\boldsymbol{\nabla} \{\varLambda_{\varSigma }(\mathbf{r})\boldsymbol{\nabla}\varLambda_{\varSigma}(\mathbf{r})\cdot\dot{\mathbf{r}} \}$. Using the properties of the gradient operator, we can write the force as

(8)

F _ind is proportional to the particle’s velocity; it is therefore a dissipative force and it is responsible for the resistive cooling of the trapped ion [20, 29]. The motional energy of the particle is ohmically dissipated by the resistance of the detection LC-circuit.

3.3 The “effective coupling distance” approximation

The force of Eq. (8) has a complex dependence on the particle’s position, r(t), through the quantity ∇ Λ _Σ (r(t)). However, if the amplitude of the particle’s motion is small compared to the dimensions of the electrode, Σ, then r(t) can be approximated by the equilibrium position: r(t)≃(0,y ₀,0). In this case, we can define the effective coupling displacement as

(9)

The introduced quantity, $\mathbf{D}_{\mathrm{eff}}^{-1}$, is a vector with three components: $\mathbf{D}_{\mathrm{eff}}^{-1}= (\frac{1}{D_{\mathrm{eff}}^{x}},\frac {1}{D_{\mathrm{eff}}^{y}},\frac{1}{D_{\mathrm{eff}}^{z}} )$. The elements, $D_{\mathrm{eff}}^{i}$, have the dimensionality of a distance, therefore each $|D_{\mathrm{eff}}^{i}|$ can be denoted as an effective coupling distance. These are functions of the dimensions of the electrode, Σ, and of the equilibrium position of the particle, y ₀. Within the effective coupling distance approximation, the second summand on the right hand side of Eq. (8) vanishes and the force simplifies to

(10)

The induced voltage can be expressed as: $V_{\mathrm{ind}}(\omega)= -q Z(\omega)\mathbf{D}_{\mathrm{eff}}^{-1}\cdot\dot{\mathbf{r}}$. Thus, in general, it is a linear combination of the three particles’s eigenfrequencies. However, the impedance of the LC-circuit, Z(ω), is usually negligible for frequencies far from the resonance. Therefore, the voltage, the induced force, and its resistive cooling effect, are only appreciable for the resonant frequency component of the particle’s motion.

3.3.1 Physical meaning of $\mathbf{D}_{\mathrm{eff}}^{-1}$.

Taking into account Eq. (6), it is clear that $\mathbf{D}_{\mathrm{eff}}^{-1}$ is simply the normalized electric field (i.e. divided by V _ind=1 volt) produced by the electrode Σ at the position of the trapped particle:

(11)

The components of $\mathbf{D}_{\mathrm{eff}}^{-1}$ might be negative quantities. However, it must be observed that the induced force (Eq. (10)) goes with the square of the coupling displacement. $\mathbf{D}_{\mathrm{eff}}^{-1}$ or equivalent quantities have been calculated for the hyperbolic [30] and cylindrical traps [31, 32]. In [27], the expression effective electrode distance has been used to denominate $|D_{\mathrm{eff}}^{z}|$ of the correction electrode of a 5-pole cylindrical trap.

3.3.2 Cooling time constant

Taking into account Eq. (10), it is straightforward to derive the resistive cooling time constant:

(12)

In Eq. (12), it has been assumed that each individual motion component i in Eq. (10) can be decoupled from the other two. This is basically always the case in 3D Penning traps. For the CPW-cavity trap though, as shown in Sect. 3.5.1 (see also Eq. (15)), it can occur that the x and y components are both resistively cooled simultaneously through the same electrode, however, with each component experiencing a different effective coupling distance, $D_{\mathrm{eff}}^{i}$. In this case, the overall cooling time constant is given by

(13)

3.3.3 Impedance of the particle + LC-circuit

Equation (13) follows from Eq. (10), but it can also be understood by taking into account that the trapped particle behaves as an equivalent series LC-circuit, connected in parallel to the detection LC [19, 20, 32]. This is sketched in Fig. 6.

Fig. 6

Equivalent electric circuit of the trapped particle interacting with the detection LC. The system is driven by the thermal Johnson noise (not shown) of the LC-circuit [32]

For each motion’s component, the equivalent inductance of the trapped particle is given by $L_{\mathrm{ion}}^{i}=\frac{m}{q^{2}} (D_{\mathrm{eff}}^{i} )^{2}$, with $1/\sqrt{L_{\mathrm{ion}}^{i}\cdot C_{\mathrm{ion}}^{i}}=\omega_{\mathrm{ion}}$ and it is related to the corresponding cooling time constant through $\tau^{i}=\frac{L_{\mathrm{ion}}^{i}}{Z(\omega )}$ [19]. Hence, the overall cooling time constant τ ^overall results from the combination of two different $L_{\mathrm{ion}}^{i}$, both connected in parallel to the external detection circuit.

In thermal equilibrium, the trapped particle produces a shortcut of the detection LC-circuit. The resonance curve of the latter appears with a dip at the frequency of the former, as illustrated in Fig. 7. The impedance curve of the ion + LC-circuit can be measured and fitted to a known function [32]. The particle’s frequency is obtained from that fit. The width of the dip is equal to the inverse of the cooling time constant Δω=1/τ [20]. Hence, in general, for the particle to become “visible”, τ must be as small as possible. This is accomplished through (a) the minimisation of $|D_{\mathrm{eff}}^{i}|$ and (b) the use of a detection coil with very high quality factor, usually superconducting [33]. The implementation of the detection LC-circuit and required amplifiers is independent of the used trap. It is discussed, for instance, in [33, 34].

Fig. 7

Impedance of the trapped particle + detection LC-circuit. The particle and the circuit are assumed resonant (see [20, 32] for further details)

3.4 Detection of the cyclotron motion, excitation and sideband-coupling

The CPW-trap is symmetric along the u _x axes, hence the induced potential at any of the central electrodes is always even symmetric along x⇒∂ _x ϕ _ind=0. This implies that $D_{\mathrm{eff}}^{x}=\infty$ for any of those electrodes: the x(t) motion cannot be detected or cooled through any of them. In contrast, the inevitable drop of ϕ _ind with the vertical distance implies that the induced potential is asymmetric along y and the derivative ∂ _y ϕ _ind does usually not vanish. Hence, $D_{\mathrm{eff}}^{y}\neq\infty$ and the motion y(t) can be detected through any of the central electrodes. However, there are some “pathological” exceptions to this. These are described in Sect. 4.

From Eq. (2) it is clear that the particle’s vertical motion, y(t), gives access to the cyclotron frequency ω _p . Thus, according to the preceding paragraph, the measurement of ω _p does not require dividing any electrode into two halves, such as in 3D traps—see, for instance, [35]—or other planar Penning traps [1, 11]. Furthermore, the cyclotron and magnetron motions can be sideband-coupled [36] to the axial motion by means of an RF-field applied to any central electrode (with the exception of the ring). Dividing one of those electrodes in two halves is not required for sideband-coupling either. This simplifies the design and fabrication of the trap.

3.5 Explicit expressions for $D_{\mathrm{eff}}^{i}$

The following paragraphs give the explicit expressions of $\mathbf{D}_{\mathrm{eff}}^{-1}$ for some electrodes and the ground-planes. Further possibilities that might also be considered are the end-caps, a half-ring and others. Here, we concentrate on the most practical options.

3.5.1 Ring electrode

The effective coupling displacement for the ring is given by:

(14)

The axial symmetry (along $\hat{u}_{z}$) of the potential induced by the electron/ion at the ring implies that $D_{\mathrm{eff}}^{z}=\infty$. Hence, the axial motion can neither be detected nor resistively cooled through this electrode. On the contrary, the cyclotron motion can be detected efficiently, thanks to the finite value of $D_{\mathrm{eff}}^{y}$ in Eq. (14).

3.5.2 Ground-plane

The expressions for the effective coupling distances are given in Eq. (15). In that equation, the symbol a ₀ represents the assumed total width of the CPW-trap, including the two (finite) ground-planes. These can be used to detect both x(t) and y(t). However, each motion has a different D _eff and, as explained in Sect. 3.3.2, the overall cooling time constant is given by Eq. (13):

(15)

3.5.3 Correction electrode

The explicit calculation of Eq. (9) for the correction electrode delivers the expressions given in Eq. (16).

(16)

4 Examples

We now study the behaviour of the different $\mathbf{D}_{\mathrm{eff}}^{-1}$ derived in Sect. 3. For this purpose, we assume a CPW-Penning trap with the following dimensions: l _r =0.9, l _c =2.0, l _e =5.0, S ₀=7.0, η=0.1, a ₀=17.0 mm. This geometry is in principle arbitrary, however, it is also used as illustrative example in [12], where it is shown that its useful trapping interval (see Sect. 2.1.2) is [0.8,2] mm. We consider the cases of a trapped proton and of a trapped electron. In Sect. 4.4 a smaller trap is also discussed.

4.1 Variation of $\mathbf{D}_{\mathrm{eff}}^{-1}$ with y ₀

Figure 8 shows the variation of $D_{\mathrm{eff}}^{y,z}$ with y ₀ for one of the correction electrodes. In this example, $D_{\mathrm{eff}}^{y}$ has a divergence around y ₀∼1 mm. This divergence illustrates the existence of one particular height for which the resistive cooling force, i.e. the induced electric field along $\hat{u}_{y}$ (see Eq. (11)) vanishes. The divergence of $D_{\mathrm{eff}}^{y}$ is exclusively determined by the geometry of the trap. As explained in Sect. 3.3.3, |D _eff| should be as small as possible. In this example, the undesired divergence falls within the useful trapping interval, making the correction electrode not appropriate for detecting the cyclotron motion of a trapped ion. Different dimensions of that electrode might shift the divergence outside that interval. The existence of such “pathological” cases must be taken into account when designing a CPW-trap.

Fig. 8

Plot of $D_{\mathrm{eff}}^{y}$ and $D_{\mathrm{eff}}^{z}$ for one correction electrode. The shadowed area covers the useful trapping interval

For the trap of the example, the cyclotron motion can be detected more efficiently via one of the ground-planes. This is clear from Fig. 9, which shows a plot of the effective coupling distances for the motions x(t) and y(t) for one ground-plane. As in Fig. 8, $|D^{y}_{\mathrm{eff}}|$ exhibits a divergent behaviour, but now the divergence is outside the useful trapping interval. Within the latter interval, the effective coupling distance has a similar magnitude for both motions, x(t) and y(t).

Fig. 9

The effective coupling distance for the motions x(t) and y(t) for one ground-plane. The useful trapping interval (shadowed region) covers a small part of the plot area

The most convenient electrode for measuring the cyclotron frequency is the ring. This can be inferred from Fig. 10, which shows $D_{\mathrm{eff}}^{y}$ when the particle’s signal is picked-up by that electrode. In this case, no divergent behaviour is observed and the effective coupling distance is smaller than the values obtained in Figs. 8 and 9. This is an expected result, since the amount of induced charge is always maximal at the ring electrode, due to its closer vicinity to the trapped particle than any other electrode.

Fig. 10

Effective coupling distance for the motion y(t) for the ring. The shadowed area is the useful trapping interval

4.2 The effective coupling distance for small y ₀

Figures 8 and 9 show that the effective coupling distances for the motions x(t) and z(t) diverge when the equilibrium position becomes very small, y ₀→0. The case of the vertical motion y(t) is different: $D_{\mathrm{eff}}^{y}$ remains finite for y ₀→0. This can be understood by taking into account that at the trap’s surface (y ₀=0) only a normal electric field can exist, due to its conducting nature. Hence, according to Eq. (11), this implies that $D_{\mathrm{eff}}^{z},D_{\mathrm{eff}}^{x}\rightarrow\infty$, while $D_{\mathrm{eff}}^{y}$ becomes minimal, but it does not diverge. This must be taken into account when designing a CPW-Penning trap, particularly when the trap is intended to operate at small y ₀. For the example trap, the useful trapping interval is located so that $D_{\mathrm{eff}}^{z}$ is not affected by that divergent behaviour (see Fig. 8), but $D_{\mathrm{eff}}^{x}$ is clearly affected, as seen in Fig. 9.

4.3 Axial dip of a single proton

In order to illustrate the detection of a “heavy” ion, we now consider the case of a proton. For the axial detection, we assume an LC-circuit with a quality factor of Q=5700 and a resonance resistance R=36 MΩ (see Fig. 5). These are real values, used in the first observation of spin-flips of a single proton in a Penning trap [37]. The corresponding width of the axial dip can be calculated using Eq. (12), thereby substituting Z(ω) by R. The result is plotted in Fig. 11. In this example, it is assumed that one compensation electrode is used for picking-up the axial signal (see Figs. 5 and 8).

Fig. 11

Width of the axial dip, $\Delta\nu_{z}=\frac{1}{2\pi\tau^{z}}$, as a function of the trap’s equilibrium position. In (b), the trap is assumed with ∼1/4 the dimensions of those in (a)

Figure 11(a) assumes a trap with the same dimensions as in Figs. 8, 9 and 10. Within the useful trapping interval of that trap ([0.8,2] mm) the width of the dip is always above 1 Hz. That is comparable or bigger than in [37], thus, in principle, clearly detectable, provided that T _c is optimally tuned [12]. In panel (b), a trap scaled down by a factor ∼4 is assumed, i.e. with l _r =0.9/4,l _c =2/4 and S ₀=7/2 mm. It can be shown that the useful trapping interval of that trap is [0.2,0.5] mm. In this case the width of the axial dip is always above ∼50 Hz. This indicates a favourable behaviour towards the potential scalability of the CPW-trap.

4.4 Cyclotron detection of a single proton

The observation of the proton’s cyclotron dip is more challenging than the axial case. This is due to the usually much lower values of the resonance resistance R and quality factor Q, attainable with LC-circuits at the higher range of frequencies around ω _p (see [33] and references therein). As an indicative example, for B=1 T the cyclotron frequency of a trapped proton amounts to ω _p ≃2π⋅15 MHz, typically 1–2 orders of magnitude bigger than ω _z .

For the small trap considered in Fig. 11(b), the width of the cyclotron dip is plotted in Fig. 13. We have assumed a detection LC-circuit with Q=1250 and R=380 kΩ. These belong to the real cyclotron detection circuit employed in [37] (resonant frequency ∼29 MHz, B=1.89 T). As seen in Fig. 12, for trapping positions below 0.25 mm the width of the cyclotron dip becomes of the order of 1 Hz, corresponding to a relative width of $\frac{\Delta \omega_{p}}{\omega_{p}}=3\cdot10^{-8}$ (at B=1.89 T). This might be observed if the fluctuations of the magnetic field are in the range of a few ppb during the required measurement time (approximately of the order of 1 min for a 1 Hz dip). That level of stability is achieved by self-shielded superconducting solenoid systems [38].

Fig. 12

Width of the cyclotron dip, $\Delta\nu_{+}=\frac{1}{2\pi\tau^{y}}$, as a function of the trap’s equilibrium position. The cyclotron signal is picked-up by the ring electrode. The trap is assumed with l _r =0.9/4,l _c =2/4 and S ₀=7/2, all in mm

The observation of an ion’s cyclotron dip is a desired goal in a broad spectrum of Penning trap experiments, particularly for measuring g-factors [21, 37, 39] or masses of stable isotopes [40]. It would allow for determining ω _p with the particle in thermal equilibrium with the cryogenic detector [41], hence minimising measurement errors caused by the finite amplitude of the ion’s motion.

For the upper range of values of y ₀, where the dip is too thin to be observable, the cyclotron signal can be detected by exciting the cyclotron motion. A good estimation of the required excitation energies can be obtained by assuming that the induced cyclotron voltage must exceed the Johnson’s noise level of the LC-circuit: $|V_{\mathrm{ind}}|= \frac{q R}{|D_{\mathrm{eff}}^{y}|}\cdot\dot{y}\geq\sqrt{4k_{B}T R\cdot B_{D}}$. Here, k _B ,T and B _D represent Boltzmann’s constant, the temperature of the LC, and the detection bandwidth (in Hz), respectively. With Eq. (2) and the expression for the cyclotron amplitude A _p [12], we obtain the following condition on the required cyclotron energy:

(17)

The minimum energy of Eq. (17) is plotted in Fig. 13. The plot is for a single proton, with a detection circuit at T=4.2 K and assuming a bandwidth of B _D =12 Hz. The values obtained are similar to those observed in real experiments with ions in 3D traps (see, for instance, [21]). It is also worth observing, that at E _p =12000 K the proton’s cyclotron amplitude amounts to ∼80 μm, i.e. much lower than the dimensions of the trap. Hence, the particle can be excited at such energies (or actually much higher) for its detection, thereby without leaving the CPW-trap or colliding with its surface.

Fig. 13

Minimum cyclotron energy for |V _ind| equal or greater than the Johnson’s noise level. The plot assumes T=4.2 K, a bandwidth B _D =12 Hz and η _p ≃1. Detection through the ring electrode, with same dimensions as in Fig. 10

4.5 Axial dip of a single electron

.

For trapping voltages around V _r ≃1 volt, the electron’s axial frequency is typically in the range of ∼30 MHz or ∼90 MHz, for the traps of Figs. 11(a) and 11(b), respectively. In general, V _r can be chosen such that the electron’s axial dip might be detected with an LC-circuit similar to the one presented in Sect. 4.4, and used in [37]. Hence, inserting the corresponding values and performing the same calculation as in Fig. 11, it can be shown that the electron’s axial dip is in the range of 40–350 Hz and 0.7–6.6 kHz, within the useful trapping interval of the bigger and smaller traps, respectively. In both cases, the electron’s axial dip is in the range where it can be observed. However, as for the proton, this critically requires that the tuning ratio is optimised, as described in [12].

4.6 Cyclotron dip of a trapped electron

The electron’s small mass implies that the cyclotron frequency usually has a value in the microwave domain (ω _p ≃2π⋅28 GHz for B=1 T). Such ω _p cannot be detected by means of an LC-circuit with lumped elements, as shown in Fig. 5. Instead, a microwave CPW-cavity can be connected to the CPW-trap and function as the detection LC-circuit.

Let us first assume a non-superconducting CPW resonator, for instance, fabricated with gold on a substrate of teflon (dielectric constant ϵ _r =2.1 and losses tanδ=0.0001). The resonance resistance of a λ/4-cavity can be estimated to [24] R≃53 kΩ, at a resonance frequency of 28 GHz. This corresponds to a quality factor of Q≃1000. Here, we have assumed a CPW as in Fig. 10, with substrate thickness 1 mm. Plugging R into Eq. (12), we estimate the width of the electron’s cyclotron dip to ∼8–30 Hz, within the trap’s useful interval ([0.8,2] mm). A small magnetic field fluctuation of 1 nT produces a change Δω _p =2π⋅28 Hz. Hence, for the dip not to become blurred by magnetic fluctuations, these should be below the 1 nT level. This represents a very severe constraint, practically not achievable in most situations. However, it can be relaxed if a superconducting CPW-cavity is employed. For temperatures below ∼2 K, these cavities achieve quality factors in the range of Q∼10⁵, with resonance resistances of the order of several MΩ [42]. A superconducting CPW-cavity with Q=10000 would increase the dip’s width towards the range 80–300 Hz. For the smaller trap of Fig. 11(b), the width of the dip would scale up to ∼500–700 Hz, within its useful interval ([0.2,0.5] mm). These results would, in principle, allow for the detection of the electron’s cyclotron dip. However, in both cases, the detection CPW-cavity must be magnetically shielded, since high Q values are only achieved in weak magnetic fields, i.e. not bigger than a few Gauss [42]. As for the proton, the observation of the electron’s cyclotron dip would be a convenient way of measuring ω _p . However, the latter can be also measured by exciting the electron, as described in Sect. 4.4.

To finalise this section, it must be noted that the electrostatic Green’s function of Eq. (4) is not valid for microwaves. Hence, Eq. (9) cannot deliver an exact value of $\mathbf{D}_{\mathrm{eff}}^{-1}$ for the electron’s cyclotron motion. The values plotted in Fig. 10 represent now only an approximation of the order of magnitude of $\mathbf{D}_{\mathrm{eff}}^{-1}$. Exact values might be obtained with Eq. (11) and the use of high frequency techniques for determining the electric field [23].

5 Conclusions

We have presented a detailed model of the effective coupling distance in a CPW-Penning trap for different electrodes. In contrast to standard 3D traps, where the particle is located at one fixed position, the detection signal in a CPW-trap strongly depends on the trapping height, y ₀. The detection of the cyclotron motion and the employment of the side-band coupling technique, do not require dividing any of the trap’s electrodes in halves. This simplifies the design and fabrication of the trap. The existence of “pathological” cases, where the effective coupling distance might diverge, must be also taken into account. Those might impede the efficient detection and resistive cooling of the trapped particle.