1 Introduction

Since Shih et al. made the first experimental observation of the self-bending of screening solitons [1], the self-bending of spatial solitons is further studied by experiment and numerical simulation method [2–14]. When the optical beam size is in the range of the charge carrier diffusion length, the diffusion effect cannot be neglected. The diffusion process introduces an asymmetric tilt in the light-induced photorefractive (PR) waveguide, which in turn affects the propagation characteristics of PR solitons. Taking the first-order diffusion effect into account, the solitons propagate following an approximately parabolic trajectory with a constant intensity profile, and the maximum intensity value of bright solitons remains approximately invariant [15]. However, experiments have indicated that these bright screening solitons can experience a considerable increase in self-deflection, especially in the regime of very high bias field strengths, when the action of higher order terms is considered. In this regime, the absolute value of the spatial shift that is due to first-order diffusion alone is always smaller than those of both first- and higher-order terms acting together, and these solitons always bend to the right [16].

With ignoring the diffusion effect, another interesting bending property of solitons (termed as “swing solitons”) in a waveguide with transverse Gaussian linear refractive index profile has recently attracted a great deal of research interest [17–19]. By using the intensity of the input beam to control the parameter of the spatial oscillation period, Garzia et al. [17] found that the spatial oscillation of solitons is a function of the intensity of the beam. Subsequently, Suryanto and Van Groesen [18] analyzed and simulated the soliton oscillation inside the waveguide with triangular linear refractive index profile. Experiments of Sheu and Shih [19] also demonstrated the relation between the swinging amplitude and frequency. Their study suggested a resonance interaction between the soliton light beam and its induced waveguide. In Ref. [20], the soliton swinging behavior has also been observed in Kerr nonlinear media. The author considers the solitons’ propagation in Kerr media with transverse harmonic modulation of the refractive index. The solitons slowly radiate upon propagation along the periodic structure and are finally trapped in one of its guiding channels with slightly oscillating propagation. The oscillation behavior of solitons relate to the initial incident angle. If the incident angle is small enough, the oscillation behavior resembles a swinging optical spatial soliton.

Obviously, the study of spatial soliton bending induced by different disturbances might be of great interest and importance in many applications, e.g., it can be made into all-optical switch acting as the detection device for optical signal processing in vibration system. In this paper, we will employ both experiment and numerical simulation to investigate the beam shifting effect on bending of bright spatial solitons in a biased transversely shifting photorefractive crystal.

2 Experiment

In our experiments we used a congruently melting SBN crystal with a concentration of 0.1 wt.% CeO2 (γ 33=225 pm/V, n e =2.27) in the melt. The dimensions of the sample were 5.7×5.9×3.6 mm3, with the 3.6 mm edges along the c axis of the crystal. The propagation length was 5.9 mm. On both faces normal to the c axis, electrodes were prepared with silver paste.

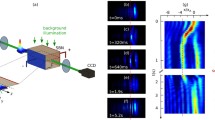
The experimental setup is shown in Fig. 1. An argon-ion laser at 488 nm and 40 mW is focused with a 20-mm focal length lens at the entrance face of the crystal to a 10 μm FWHM spot. The laser beam propagates in the sample along the z-axis with the polarization parallel to the optical axis. In the case, the sample is fixed on a shifter controlled by a stepping motor in such a way that the sample will shift along with the shifter. When the sample shifts along the positive optical axis, the propagating beam will shift to the inverse direction (negative optical axis).

Fig. 1
figure 1

Experimental setup, in which the shape (side-view picture) of the beam was imaged by a 25× microscope lens on a calibrated CCD camera

Full size image

Launched into the biased transversely shifting photorefractive crystal, a naturally diffracted laser beam is observed to promptly trap into bright solitons and then bend to the beam shifting side. At last, the bending beam arrives at maximum amplitude at the crystal exit face and keeps this situation invariant until the shifting movement stops. Thus, we consider that the beam at the maximum bending amplitude shares the same shifting velocity with the sample. When the shifting direction of beam is inverted at the maximum bending amplitude, the beam will deflect to another side, which resembles the “swinging solitons” recorded in the literature [17, 18]. While the polarity of the applied electrical field is reversed, the beam self-defocussing is also observed and slightly deflected during the transverse shifting of the sample. Typical experimental results are presented in Fig. 2. The bending amplitude of the soliton beam at the crystal exit face of about 290 μm is observed with a shifting velocity of v x =9×10−5m/s and the transverse electrical field of about 4.2 kV/cm. Figure 2(b) also shows the slightly deflected self-defocussing beam. In our research, the bending of self-defocussing beam is still not fully understood and needs more investigation. However, it is affirmative that the transverse shifting of the sample can induce the refractive index change of the propagated beam.

Fig. 2
figure 2

(a) A naturally diffracted laser beam at 488 nm prorogating in crystal; (b) the slightly deflected self-defocussing beam; (c)–(e) the bending solitons, in which the applied electrical field is about 4.2 kV/cm, the shifting velocity is about v x =9×10−5 m/s

Full size image

Obviously, the transverse shifting can affect the self-trapping and the bending of the beam. In our experiments, it is found that the self-trapping of the beam will travel less time when the transversely shifting velocity of the beam is higher. The formation time of soliton is only 9.5 s when the transversely shifting velocity is 9×10−5 m/s with E=4.2 kV/cm, which is faster in any case than at a shifting velocity of less than 9×10−5 m/s. It is suggested that the transverse shifting of the beam (sample) can accelerate the self-trapping of the propagating beam in a biased photorefractive crystal. However, the amplitude of the soliton tends to an inverse change. At a higher shifting velocity, the bending amplitude of the soliton will be decreased. Figure 3(a) shows the soliton formation time versus shifting velocity, and Fig. 3(b) shows the response curves of the bending amplitude observed at the crystal exit face versus the transversely shifting velocity, in which the shifting velocity is from 8×10−5 m/s to 13.5×10−5 m/s with Δv x =0.25×10−5 m/s and the applied external field is about E=4.2 kV/cm.

Fig. 3
figure 3

(a) The soliton formation time versus shifting velocity; (b) the response curves of the bending amplitude observed at the crystal exit face versus the transversely shifting velocity, in which the shifting velocity is from 8×10−5 m/s to 13.5×10−5 m/s with Δv x =0.25×10−5 m/s and the applied external field is about E=4.2 kV/cm

Full size image

It should be pointed out that no background light beam is used in our experiment. As long as the movement has not ceased, the shifting can promote the soliton formation and maintain it, which is different from other soliton cases. It should be a new type of soliton. Here we term it as “velocity soliton,” which differs from the ordinary photorefractive screening soliton. We regard that the shifting process introduces an asymmetric tilt in the light-induced photorefractive waveguide, which in turn affects the propagation characteristics of photorefractive solitons. Figure 3(b) suggests that the outside transversely shifting velocity influences the free-carrier diffusion speed and spatial electric field creation time. A higher shifting velocity can effectively shorten the time of the saturable refractive index change. The light excites charges, which migrate in the presence of the external electric field as well as velocity field, and are captured (recombine) by deep (ionized donors or acceptors) traps. The shape of the light beam gives rise to nonuniform trapping and bending, which is mainly attributed to the nonuniform screening of the external electric field and the nonlinear relaxation effect present in the samples. Just as in photorefractive screening soliton formation, the formed spatial electric field modifies the refractive index via the linear electro-optic (Pockel’s) effect and traps the beam. Moreover, the nonlinear relaxation effect excited by the shifting governs the saturable refractive index change, which results in the bending of the soliton. Obviously, the bending amplitude of the soliton should relate to the shifting velocity. In the next part, we discuss the relation between the shifting velocity and the bending of spatial bright solitons.

3 Simulation analysis

In order to further understand the dynamic behavior of the soliton beam in a biased transversely shifting photorefractive crystal, we adopt the (1+1)-dimensional simplified beam propagation method to study systematically the velocity effect of the bending solitons, and we assume that the solitons are spatial bright ones (Δn<0). The incident light beam is simulated by the beam propagation algorithm from the input face to the output face with the nonlinear paraxial wave equation:

(1)

where A is the amplitude of the electric field of the soliton beam; x the transverse coordinate; z the propagation axis; n b the unperturbed refractive index; k=2πn b /λ is the wave vector. The saturable refractive index change δn is governed by a relaxation form equation [19, 21]:

(2)

where τ is the relaxation time of the nonlinearity and γ is the nonlinear coefficient required to form the solitons, \(\gamma = \frac{1}{2}n_{b}^{3}\gamma_{33}E\). In turn, the envelope propagation equation can be obtained by substituting the expression for the perturbed refractive index (induced by the space-charge field) into the paraxial wave equation:

(3)

The low-amplitude case also deserves special consideration. In this limit, Eq. (3) is given by

(4)

Introducing the uniform transformation

(5)

B(X,Z) satisfies:

(6)

where the perturbation potential V is given by

(7)

Equation (6) is normalized NLS equation with an additional term in the right-hand side. In the absence of perturbations, i.e. t=0, then V=|B|2, and then the NLS equation (6) changes into normalized LS equation, which implies the input light wave is a planar wave. If we assume that the shifting velocity is constant, then the time t is a function of x,t=x/v x , and Eq. (7) with neglecting second and higher terms of \(e^{ - \frac{\bar{X}}{k\tau v_{x}}}\) can be rewritten as:

(8)

To analyze the modified NLS equation (6), we apply the equivalent-particle theory. The exact expression for the rate of change of the normalized dimensionless power is

(9)

The average position:

(10)

The average velocity:

(11)

If the B(X,Y) evolves according to the NLS equation (6), the following expressions are exact:

(12a)
(12b)
(12c)

It is obvious that we can completely describe the behavior of a soliton beam in a refractive index profile by using the analytical expression of Eq. (12c). Reviewing our experiments, we find that the soliton bending takes place after the soliton formation, which means that the soliton stabilizes itself around the equilibrium condition before bending. To analyze the soliton bending in the presence of the outside disturbance (transverse shifting of the beam), we suppose that the input wave-packet is a single soliton; the approximation for its propagation is taken as:

(13)

where \(\upsilon(Z) = \frac{d\bar{X}}{dZ}\), \(\sigma(Z) = \frac{r^{2} - \upsilon (Z)^{2}}{2}\).

The acceleration \(a = \frac{d^{2}\bar{X}}{dZ^{2}}\) can be found by substituting (8) and (13) into (12c):

(14)

In our case, the direction of the shifting beam keeps in line with the shifting velocity and 3β>r 2. Figure 4(a) shows the acceleration profiles for different velocities v x with τ=1, and 3β−r 2=0.5. As is illustrated, the maximum of the acceleration occurs at the position \(\bar{X} = 0 \) and can be acquired according to Eq. (15):

(15)
Fig. 4
figure 4

(a) Acceleration profile for different shifting velocities. (b) The response curve of the transverse distance X versus V e for η=0.12, z=Z/k=5.9 mm (z is the propagating length of the crystal)

Full size image

Although it seems that the bigger soliton bending is observed near the entrance face, the center of the beam profile at the input face keeps almost invariable. In fact, the transverse acceleration \(\frac{d^{2}\bar{X}}{dZ^{2}}\) and the shifting velocity V e share the same direction, which can be judged by Fig. 3. In Fig. 4(a) it is also found that the transverse acceleration (depending on the average position \(\bar{X}\)) tends to zero when the beam experiences a large transverse shift. At this time, the soliton beam has to propagate along the z-axis in the transversely shifting sample with the final transversely shifting velocity v x (equal to the shifting velocity of the sample) and the maximum bending amplitude \(\bar{X}_{m}\).

To acquire the position \(\bar{X}_{m}\) of the acceleration equal to zero, the Taylor expansion at \(\bar{X} = 0\) of Eq. (14) is adopted by neglecting the fourth- and higher-order terms of \(e^{ - \frac{\bar{X}}{V_{e}}}\). We obtain the following acceleration equation:

(16)

When \(a(\bar{X}) = 0\), the approximate solution of maximum deflection distance \(\bar{X}_{m}\) of Eq. (16) is:

(17)

Since the transverse acceleration is a function of the variable X, the mean acceleration a m can be considered as the following:

(18)

where d is the initial position of the beam with respect to the center of the index profile. Equation (16) allows us to know the maximum deflection of the soliton beam with a velocity equal to v x . By substituting (14) into (18) and solving the integral, we can obtain the analytical expression of the mean acceleration a m :

(19)

The transverse distance X as a function of propagation coordinate Z [17] is

(20)

Figure 4(b) depicts the \(\bar{X}\sim V_{e}\) curve, where the η=0.12 and Z is supposed to be the maximum propagation length of the beam in crystal. Comparing with the response curves of Fig. 3(b), we find that the result is coincident with experimental observation.

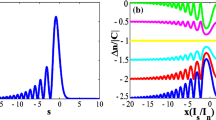
Thus, the profile of the formed soliton can be proximally expressed as:

(21)

In Fig. 5 we show the simulated results for different shifting velocities. These numerical results also perfectly agree with the above analysis.

Fig. 5
figure 5

(a) Numerical simulation for r=0.4, η(r)=0.12, V e =±8×10−1. (b) Numerical simulation for different shifting velocities and r=0.4, η(r)=0.12

Full size image

4 Summary

In summary, we have measured and simulated the dynamic evolution of a beam that is launched into a biased transversely shifting photorefractive crystal. The experiments and the simulation show fairly good agreement. The transverse shifting of the beam (sample) can accelerate self-trapping of the propagating beam. However, the bending amplitude of the soliton tends to an inverse change. At a higher shifting velocity, the bending amplitude of the soliton beam tends to be decreased. The study of the beam shifting effects on bending of bright spatial solitons in a biased transversely shifting photorefractive crystal provides a method to further understand the dynamic behavior of a propagating beam under different disturbances.