1 Introduction

In the last decade, knowledge about electromagnetic (EM) waves expanded quickly as a new concept, metamaterial, was introduced [1–11]. In these metamaterials, the propagation of EM waves exhibits a lot of unique properties, leading to some extraordinary applications, for instance, subwavelength lensing, electromagnetic cloaking, and so on [6–11]. Metamaterials include double-negative (DNG) metamaterials (with simultaneously negative permittivity ε and permeability μ) and single-negative (SNG) metamaterials. There are two kinds of SNG materials: the ε-negative (ENG) and the μ-negative (MNG) media. It is well known that EM waves in an isolated SNG material are evanescent since their wave vectors are imaginary. But transmission bands were found in one-dimensional (1D) periodic structures composed of alternating layers of positive-index materials and single-negative materials [12–14]. However, the frequencies of such transmission bands are sensitive to the incident angle, making these periodic structures inefficient in the case of multidirectional filtering. On the other hand, tunneling modes with weak angular dependence could be generated in 1D layered structures consisting of SNG materials [15–18]. However, the periodicity of these SNG structures has to be broken, for example, by introducing defects in the structures, to produce such tunneling modes. Creating omnidirectional transmission modes in a simple periodic layered structure is still a problem to be solved. In this paper, a 1D periodic structure consisting of alternating layers of DNG and MNG materials is proposed. Such a structure can produce a number of transmission modes, whose number, frequencies and frequency intervals can be controlled by changing its structural parameters. These transmission modes with perfect transmission are insensitive to the incident angle. Experiments based on composite right/left-handed transmission lines were carried out to verify the theoretical results. These unique properties of the periodic metamaterial layers can be used to design multichannel and omnidirectional filters.

2 The model

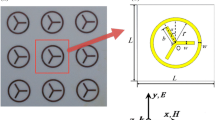
A 1D periodic structure composed of DNG and MNG materials is shown in Fig. 1. We denote the 1D periodic structure by (AB)S, where A represents a layer of DNG material with the thickness of d A and B represents a layer of MNG material with the thickness of d B , and S is the number of periods. We use the Drude model to describe the parameters of the isotropic metamaterials [1–5], that is,

$$ \varepsilon_{A} = 1 - \frac{\omega_{Aep}^{2}}{\omega^{2}}, \qquad \mu_{A} = 1 - \frac{\omega_{Amp}^{2}}{\omega^{2}} $$
(1)

in DNG materials,

$$ \varepsilon_{B} = 1, \qquad \mu_{B} = 1 - \frac{\omega_{Bmp}^{2}}{\omega^{2}} $$
(2)

in MNG materials, where ω Aep is the electronic plasma frequency for A, ω Amp and ω Bmp are the respective magnetic plasma frequencies for A and B. The working frequencies are chosen to satisfy the conditions \(\omega^{2} < \omega_{Aep}^{2}\), \(\omega^{2} < \omega_{Amp}^{2}\) and \(\omega^{2} < \omega_{Bmp}^{2}\). In this situation, the considered structure becomes a periodic DNG-MNG layered structure.

Fig. 1
figure 1

Schematic representation of a periodic structure constituted by DNG and SNG materials. The gray and white regions represent the DNG and MNG materials, respectively

Full size image

Let a plane wave be injected from vacuum into the considered structure at an angle θ with +z direction, as shown in Fig. 1. For the transverse electric (TE) [or transverse magnetic (TM)] wave, the electric field [or the magnetic field] is in the x direction. For an infinite periodic structure (AB)S (S→∞), the dispersion relation can be obtained by using the Bloch–Floquet theorem [19]:

(3)

where β z is the z component of Bloch wave vector, \(k_{jz} = \omega/c\sqrt{\varepsilon_{j}} \sqrt{\mu_{j}} \sqrt{1 - (\sin^{2}\theta/\varepsilon_{j}\mu_{j})} (j = A, B)\) is the z component of the wave vector, and c is the light speed in the vacuum. For TE wave, \(q_{j} = \sqrt{\varepsilon_{j}} /\sqrt{\mu_{j}} \sqrt{1 - (\sin^{2}\theta/\varepsilon_{j}\mu_{j})}\); for TM wave, \(q_{j} = \sqrt{\mu_{j}} /\sqrt{\varepsilon_{j}} \sqrt{1 - (\sin^{2}\theta/\varepsilon_{j}\mu_{j})}\). The EM fields in the considered system can be propagating or evanescent, corresponding to real or imaginary Bloch wave numbers. The solution of Eq. (3) defines the band structure for the infinite system (AB)S. By combining Eqs. (1) and (2), we have

(4)
(5)

Similarly, q j for layers A and B can be also obtained. Since both k jz and q j are functions of ω, the value of the right-hand side of Eq. (3) depends on ω.

3 Numerical results and discussion

In the following calculation, we choose ω Aep =1011 rad/s, ω Amp =ω Bmp =8×1010 rad/s. Figure 2(a) shows the dependence of the band structure on the incident angle in infinite structure (AB)S with d A =2.4 mm and d B =5 mm. The gray areas represent the regions of propagating states, whereas the white areas represent the regions containing evanescent states. It can be seen that several transmission bands exist. The transmission band in the higher frequency range (3.8×1010<ω<5.9×1010 rad/s) is sensitive to the incident angle. However, the transmission bands in the lower frequency range are almost robust against the incident angles for both polarizations. To confirm the above results, the transmission spectrum of the finite structure (AB)6 at normal incidence is shown in Fig. 2(b). The transmittance is calculated by using the transfer matrix method [20].

Fig. 2
figure 2

(a) Photonic band structure as a function of the incident angle in infinite structure (AB)S with d A =2.4 mm and d B =5 mm. (b) Transmission spectrum of the finite structure (AB)6 with d A =2.4 mm and d B =5 mm at normal incidence

Full size image

The physical mechanism of the transmission bands is different from the tunneling mechanism of the ENG-MNG multilayered periodic structure [14–16]. When a plane wave is incident from a DNG layer into a SNG layer, strong reflection will occur at the interface. Although fields in each SNG layer are decaying, some of them can still couple into the next DNG layer. So reflected waves exist at interfaces from DNG to SNG layers. The phase difference between two neighboring reflected waves is approximately equal to 2k Az d A +π. When the phase difference equals to odd times of π, meaning that k Az d A =nπ, these reflected waves will cancel each other and thus the transmission bands form. In the higher frequency range, the wave vector k Az depends on the incident angle θ, as shown in Eq. (4), so the central frequency of the transmission band varies as the incident angle changes. However, in the low frequency range, we can obtain from Eq. (4) that k Az ≈−ω Aep ω Amp /(ωc) and the incident angle θ is not involved in k Az , so the transmission bands are independent of the incident angle. Moreover, the central frequencies of the transmission bands can be calculated. In low frequency range (ω≪ω Aep ,ω Amp ,ω Bmp ), expressions for k jz and q j can be simplified by some approximations, \(\sqrt{1 - \omega_{Aep}^{2}/\omega^{2}} \approx i\omega_{Aep}/\omega\), \(\sqrt{1 - \omega_{Amp}^{2}/\omega^{2}} \approx i\omega_{Amp}/\omega\), \(\sqrt{1 - \omega_{Bmp}^{2}/\omega^{2}} \approx i\omega_{Bmp}/\omega\), and \(\sqrt{1 - \sin^{2}\theta/[(1 - \omega_{Aep}^{2}/\omega^{2}) (1 - \omega_{Amp}^{2}/\omega^{2})]}\allowbreak \approx1\), \(\sqrt{1 - \sin^{2}\theta/(1 - \omega_{Bmp}^{2}/\omega^{2})} \approx 1\), where \(i = \sqrt{ - 1}\). So we get k Az ≈−ω Aep ω Amp /(ωc), k Bz ≈iω Bmp /c, q A =ω Aep /ω Amp , and q B =ω/(iω Bmp ). Then Eq. (3) can be approximately simplified to

(6)

The condition of Eq. (6) having real solution for β z is |cosβ z (d A +d B )|≤1, which corresponds to the transmission band. There are two terms on the right-hand side of Eq. (6). In frequency range around the value of ω, which satisfies ω Aep ω Amp d A /(ωc)=nπ, the second term on the right-hand side of Eq. (6) is close to zero. In such a frequency range, the absolute value of the first term can be less then 1 if the parameters d A and d B are properly chosen; then a transmission band appears. As the integer n varies, transmission bands emerge in different frequency ranges. Thus the central frequencies of the transmission bands should be close to the values of ω satisfying

$$ \frac{\omega_{Aep}\omega_{Amp}d_{A}}{\omega c} = n\pi. $$
(7)

By substituting ω Aep , ω Amp and d A into Eq. (7), we have

$$ \omega= \frac{6.4}{n\pi} \times10^{10}\mbox{ rad/s} \quad (n = 1,2,3, \ldots). $$
(8)

It can be obtained from Eq. (8) that ω=2.04×1010, 1.02×1010 and 6.79×109 rad/s corresponding to n=1, 2 and 3. Such calculated results are in accordance with the positions of the transmission bands in Fig. 2. It is seen from Eq. (8) that, as n increases, more transmission bands will appear in the lower frequencies ω. As Eqs. (7) and (8) do not include the incident angle θ, these transmission bands are independent of θ. On the other hand, the transmission band in the high frequency range (3.8×1010<ω<5.9×1010 rad/s) does not satisfy the condition ω≪ω Aep ,ω Amp ,ω Bmp , so the approximations in case of low frequencies are not suitable for this band. Thus it does not satisfy Eqs. (7) and (8) and is sensitive to the incident angle. In the following investigation, we focus on the transmission band corresponding to n=3.

Figure 3 shows the dependence of the transmission band corresponding to n=3 on period number S in structure (AB)S with d A =2.4 mm and d B =5 mm. It can be seen that there are S–1 peaks in the transmission band, whatever the value of S is. Such a phenomenon comes from the interference of the reflected waves produced at the interface from DNG to SNG layers. Hence we can generate as many transmission modes as desired simply by adjusting the period number S of (AB)S. In the lossless cases, the transmittance of the modes can reach 1. To show how the transmission modes generate in the structure, Fig. 4 exhibits the field distributions corresponding to the three transmission modes in Fig. 3(c). The frequencies of these transmission modes are 6.609×109,6.644×109, and 6.681×109 rad/s, respectively. As shown in Fig. 4, the fields are mainly localized inside the DNG layers. Such property is quite different from that of the ENG-MNG multilayer structures. The fields corresponding to the tunneling modes in the ENG-MNG periodic structure are mainly localized at the interfaces between the SNG layers [15–17].

Fig. 3
figure 3

Dependence of the transmission band corresponding to n=3 on period number S in finite structure (AB)S with d A =2.4 mm and d B =5 mm

Full size image
Fig. 4
figure 4

The electric field distributions corresponding to the three transmission modes in structure (AB)4 in Fig. 3(c). The gray and white regions represent the DNG and MNG materials, respectively

Full size image

Figure 5 gives the dependence of the transmission band corresponding to n=3 on the incident angle in structure (AB)6 with d A =2.4 mm and d B =5 mm. It can be seen from Fig. 5 that, as the incident angle varies, the transmission modes all remain invariant. Such properties are in accordance with Fig. 2(a), in which the frequency range of the 3rd transmission band is shown to be insensitive to the incident angle. These omnidirectional transmission modes may be useful for designing multichannel and omnidirectional filters.

Fig. 5
figure 5

Transmittance vs. incident angles and frequencies of the structure (AB)6 with d A =2.4 mm and d B =5 mm

Full size image

Next, we investigate the dependence of the transmission modes on d A . Figure 6 shows the transmission spectra of structure (AB)6 with d B =5 mm and different d A . It is seen from Fig. 6 that, as d A increases, the transmission modes all shift to higher frequencies and the frequency intervals of the two adjacent modes remain almost unchanged. Such a result is in accordance with Eq. (7) and can be understood as follows. As mentioned before, if k Az d A =nπ is satisfied, any two neighboring reflected waves produced at the interfaces from DNG to SNG layers will cancel each other by interference and a transmission band appears. For the nth transmission band, the integer n is kept constant, so k Az decreases as d A increases. In the low-frequency case, k Az ≈−ω Aep ω Amp /(ωc), so the central frequency ω of the transmission band increases as d A increases, as shown in Fig. 6. In addition, the dependence of the transmission modes on d B in structure (AB)6 with d A =2.4 mm is also investigated, as shown in Fig. 7. It is seen that, as d B increases, the frequency intervals of transmission modes become smaller and smaller. The phenomenon in Fig. 7 can be explained using the tight-binding (TB) approach [21]. As mentioned before, the DNG layers can be seen as defect layers which possess corresponding eigenmodes. From the view of the TB approach, when these DNG layers are placed together, the interaction of the eigenmodes result in their splitting in frequencies, which leads to narrow transmission peaks. The greater the distance between the DNG layers, the weaker the interaction of eigenmodes, the smaller the frequency split, and thus the closer the interval of the transmission peaks. Using such property, one may change the frequency interval of the transmission modes by varying d B . The properties of the transmission modes in Figs. 3, 6 and 7 are very useful for the design of multichannel filters with specific channels.

Fig. 6
figure 6

Dependence of the transmission modes on d A in structure (AB)6 with d B =5 mm

Full size image
Fig. 7
figure 7

Dependence of the transmission modes on d B in structure (AB)6 with d A =2.4 mm

Full size image

In practice, losses in the metamaterials are inevitable. When losses are involved, the parameters of DNG materials in Eq. (1) should be modified as \(\varepsilon_{A} = 1 - \omega_{Aep}^{2}/(\omega^{2} - i\omega\gamma_{1})\), \(\mu_{A} = 1 - \omega_{Amp}^{2}/(\omega^{2} - i\omega\gamma_{2})\), and the permeability of the MNG materials in Eq. (2) should be modified as \(\mu_{B} = 1 - \omega_{Bmp}^{2}/(\omega^{2} - i\omega\gamma_{3})\), where γ i (i=1, 2, or 3) is the damping factor that contributes to the absorption and losses. Here we assume that γ 1=γ 2=γ 3=γ=3×105 Hz [3]. Figure 8 shows the dependence of the transmission modes on period number S in (AB)S when the losses are considered. As shown in Fig. 8, the resonance transmission still exists although the transmittance can no longer reach 1 because of the losses. We also investigate the dependence of the transmission modes on the damping factor γ in (AB)4, as shown in Fig. 9. It is seen that as γ increases, the transmission peaks drop evidently while their frequencies remain unchanged.

Fig. 8
figure 8

Dependence of the transmission modes on period number S in (AB)S with d A =2.4 mm, d B =4 mm and γ=3×105 Hz

Full size image
Fig. 9
figure 9

Dependence of the transmission modes on the damping factor γ in (AB)4 with d A =2.4 mm, d B =4 mm

Full size image

Furthermore, the periodic DNG-ENG structures are also investigated. It is found that the properties of the transmission modes in periodic DNG-ENG structures are similar to those in DNG-MNG structures, although the frequencies of the transmission modes are different due to the change of frequency dependence of the permittivity and permeability of the SNG materials.

4 Experimental design and measured results

Two main approaches to form metamaterials have been reported: resonant structures made of arrays of metallic resonators [1–3] and non-resonant transmission line (TL) structures loaded with lumped elements [22–25]. Transmission line loaded with lumped element series capacitors C and shunt inductors L, as depicted in Fig. 10, possesses both left-handed and right-handed attributes, known as composite right/left-handed transmission line (CRLH TL).SNG characteristic can be realized in the frequency range between the right-handed and left-handed passbands of the CRLH TL [22, 23].When the average lattice constant l i is much smaller than the guided wavelength λ g , the structure exhibits a macroscopic behavior which can be rigorously characterized in terms of the constitutive parameters ε and μ. In practice, l i <λ g /4 can be considered as the sufficient condition for the validity of homogeneous approximation [25]. In our experiments, 50 Ω TL was used to fabricate CRLH TL which has FR-4 substrates with thickness h=1.6 mm and relative permittivity ε sub =4.75. The thickness of copper strip on the FR-4 substrate was t=0.018 mm. The width of the copper strip was w=2.945 mm corresponding to the characteristic impedance of Z 0=50 Ω.

Fig. 10
figure 10

The schematic circuit model of a CRLH TL unit with the loading lumped elements of series capacitors and a shunt inductor

Full size image

For a CRLH TL fabricated by cascading the unit cells of Fig. 10 periodically, the effective relative permittivity and permeability are given by the following approximate expressions [22]:

$$ \begin{aligned}[c] &\varepsilon_{i} \approx\bigl(C_{0} - 1/ \omega^{2}L_{i}l_{i}\bigr)/(\varepsilon_{0}p), \qquad \\ & \mu_{i} \approx p\bigl(L_{0} - 1/\omega^{2}C_{i}l_{i} \bigr)/\mu_{0}, \end{aligned} $$
(9)

where p is a structure constant given by \(p = \sqrt{\mu_{0}/(\varepsilon_{0}\varepsilon_{re})} /\allowbreak Z_{0}\) [25], C 0 and L 0 represent the distributed capacitance and inductance of the host TL, and i represents the type of the CRLH TLs. For the microstrip lines considered here, the effective relative dielectric constant ε re ≈3.556 [26]. As a result, we can obtain the parameters p=3.99, \(C_{0} = \sqrt{\varepsilon_{re}\varepsilon_{0}\mu_{0}} /Z_{0} \approx128\mbox{ pF/m}\), and \(L_{0} = Z_{0}^{2} \times C_{0} \approx320\mbox{ nH/m}\).

Two types of CRLH TLs with 10 unit cells were designed and fabricated, as shown in Fig. 11. TL1 possesses a unit length of l 1=6 mm and loaded lumped elements C 1=1 pF and L 1=2.7 nH, and TL2 has a unit length of l 2=10 mm and loaded lumped elements C 2=1 pF and L 2=10 nH.

Fig. 11
figure 11

Photograph of the fabricated (a) DNG TL with unit length l 1=6 mm, and (b) MNG TL with unit length l 2=10 mm

Full size image

The calculated relative permittivity ε 1 and permeability μ 1 of TL1 are presented in Fig. 12(a). The simulated (by Advanced Design System (ADS)) and measured (by Agilent 8720ES S-parameter Network Analyzer) S 21 parameters for TL1 are shown in Fig. 12(b). It is seen that both ε 1 and μ 1 are negative when the frequency is lower than 3.5 GHz and a left-handed passband appears. TL1 can be equivalent to DNG material within the left-handed passband and it is denoted as DNG TL. There is a cutoff frequency \(f_{c} = 1/(4\pi\sqrt{L_{i}C_{i}} )\) for such high-pass CRLH TL [22]. Therefore, the propagation of EM wave is prohibited when the frequency is lower than the cutoff frequency at about 1.28 GHz, as shown in Fig. 12(b). Figure 13(a) shows the dependence of ε 2 and μ 2 on frequency and Fig. 13(b) shows the simulated and measured transmittance for TL2.It can be seen that a stop band appears in the frequency range 1.41–2.81 GHz in which ε 2>0 and μ 2<0.So TL2 can be equivalent to an MNG material within the stop band and it is denoted as MNG TL. Although the measured spectrum shifts a little to higher frequency in comparison with the simulated one because of the error of the real lumped elements, the simulations and measurements agree well with each other. The common working frequency range for both DNG and MNG TLs is about 1.4–2.8 GHz.

Fig. 12
figure 12

(a) The calculated effective permittivity and permeability, and (b) the simulated and measured transmittance of the DNG TL with the loading series capacitors C 1=1 pF and shunt inductors L 1=2.7 nH

Full size image
Fig. 13
figure 13

(a) The calculated effective permittivity and permeability, (b) the simulated and measured transmittance of the MNG TL with the loading series capacitors C 2=1 pF and shunt inductors L 2=10 nH

Full size image

Next, we use the DNG and MNG units to construct periodic structures. For convenience, we use (DNG m -MNG n )S to denote the artificial periodic structures: m and n are the numbers of the DNG and MNG units in each period, respectively, and S is the number of periods. Three kinds of structures, (DNG2-MNG2)2, (DNG2-MNG2)3, and (DNG2-MNG2)4, were fabricated, as shown in Fig. 14. The simulated and measured S parameters of the fabricated structures are shown in Fig. 15. It is seen from Fig. 15(a) that a resonance transmission mode appears in the middle of the working frequency range 1.4–2.8 GHz of the structure (DNG2-MNG2)2. As the period number S increases, the number of the transmission modes increases as well and S-1 transmission peaks appear, in accordance with the theoretical results shown in Figs. 3 and 8.

Fig. 14
figure 14

Photograph of the fabricated periodic structures: (a) (DNG2-MNG2)2, (b) (DNG2-MNG2)3, and (c) (DNG2-MNG2)4

Full size image
Fig. 15
figure 15

The simulated and measured transmittance of the structures: (a) (DNG2-MNG2)2, (b) (DNG2-MNG2)3, and (c) (DNG2-MNG2)4

Full size image

We then experimentally study the dependence of the transmission modes as a function of the thicknesses of DNG layers by the use of CRLH TL structures. Periodic metamaterial layer structures (DNG1-MNG2)3, (DNG2-MNG2)3, and (DNG3-MNG2)3 were fabricated, as shown in Fig. 16. As discussed above, two transmission modes will appear when the period number S=3. The simulated and measured S21 parameters of the fabricated structures are shown in Fig. 17. It is seen from the simulated results in Fig. 17(a) that transmission modes 1 and 2 appear at 1.85 and 2.05 GHz, respectively. Comparing to the simulated results, the measured transmission peaks have a little blue shift. As the length of the DNG material increases, both transmission modes shift to higher frequencies. Such a result agrees well with the theoretical one that is shown in Fig. 6.

Fig. 16
figure 16

Photograph of the fabricated periodic structures: (a) (DNG1-MNG2)3, (b) (DNG2-MNG2)3, and (c) (DNG3-MNG2)3

Full size image
Fig. 17
figure 17

The simulated and measured transmittance of the structures: (a) (DNG1-MNG2)3, (b) (DNG2-MNG2)3, and (c) (DNG3-MNG2)3

Full size image

5 Conclusion

In summary, multichannel and omnidirectional transmission can be realized in one-dimensional periodic structure consisting of alternating layers of DNG and MNG materials. The number of the transmission modes can be adjusted by varying the period number of the structure. The frequencies and frequency intervals of the modes can be controlled by changing the thicknesses of the DNG and MNG layers. Moreover, the frequencies of these transmission modes are insensitive to the incident angle, which can be utilized to design multichannel and omnidirectional filters. Experimental results agree with the theoretical ones.