1 Introduction

Penning traps are widely used as storage devices for charged particles in the fields of analytical and precision mass spectrometry [1–3]. They confine particles with a charge-to-mass ratio q/m due to the superposition of a homogeneous magnetic field B along the axial \(\hat{z}\)-direction and an electrostatic quadrupolar potential Φ=U(2z 2−x 2−y 2)/d 2, where U is the potential difference between the endcap and ring electrodes. d describes the characteristic trap dimension [4]. The resulting ion motion is a superposition of three independent harmonic oscillators with an axial frequency \(\nu_{z}=1/2\pi\sqrt{qU/md^{2}}\), a magnetron frequency \(\nu_{-}=1/2(\nu_{c} - \sqrt{\nu_{c}^{2} -2\nu_{z}^{2}})\) and a modified cyclotron frequency \(\nu_{+} =1/2(\nu_{c} + \sqrt{\nu_{c}^{2} -2\nu_{z}^{2}})\) [4], where ν c =qB/(2πm) is the cyclotron frequency in the absence of an electric trapping potential. Application of a one- or two-pulse (Ramsey) azimuthal quadrupolar excitation field causes a coupling of the two radial eigenmodes, most efficiently at the sum frequency ν c =ν ++ν − [5, 6]. For the determination of the cyclotron frequency ν c and thus the mass of the ion of interest the excitation frequency ν exc of the quadrupolar excitation field is tuned around the sum frequency while monitoring the cyclotron radius. The radial eigenmotion can be detected with the time-of-flight ion cyclotron resonance method (ToF-ICR) [7] or with the Fourier transform ion cyclotron resonance (FT-ICR) technique [1, 8, 9].

In (ν ++ν −)-sideband mass spectrometry conventionally the ToF detection technique has been applied to measure many masses of stable as well as unstable nuclei with high accuracy [2]. This method is used at different facilities such as CPT [10], ISOLTRAP [11], JYFLTRAP [12], LEBIT [13], SHIPTRAP [14, 15], SMILETRAP [16], TITAN [17] and TRIGA-TRAP [18, 19]. A reduction of the uncertainty on the resonance frequency determination is achieved by applying Ramsey’s method of separated oscillatory fields [20, 21] compared to conventional one-pulse excitation [16, 22–25].

In this article we report on one- and two-pulse (Ramsey) excitation schemes using the dipolar FT-ICR detection method to monitor the coupling between the magnetron and the cyclotron motion. We investigate the influence of the excitation parameters such as rf amplitude, excitation time and waiting time on the FT-ICR signal intensity at the modified cyclotron frequency as a function of the excitation frequency for both quadrupolar excitation schemes with 7Li+ ions.

2 Description of the azimuthal ion motion during interconversion by quadrupolar rf-fields

This section provides some of the theoretical background required for the measurements.

2.1 General formalism

In a Penning trap the radial motions of an ion are best described in terms of the complex amplitudes α +(t)=|α +(t)|exp[−i(ω + t+χ +)] for the cyclotron mode and α −(t)=|α −(t)|exp[+i(ω − t+χ −)] for the magnetron mode, with ω ±=2πν ± [5]. These amplitudes are related to the Cartesian coordinates x,y by

(1)
(2)

where A is normalization constant, and where the asterisk denotes the complex conjugate.

In a quantum-mechanical context, choosing \(A= \sqrt{2\hbar /(m\omega_{1})}\), where ħ is Planck’s constant, m the ion mass, and \(\omega_{1}=\sqrt{\omega_{c}^{2}-2\omega_{z}^{2}}\), the classical amplitudes α ±(t) and \(\alpha_{\pm}^{\ast}(t)\) can be interpreted as the expectation values of the quantum-mechanical annihilation and creation operators for oscillator quanta, \(\hat{a}_{\pm }(t)\) and \(\hat{a}_{\pm}^{\dagger}(t)\), respectively, with respect to a quasi-classical coherent state |α ±〉 [26]. Using the Heisenberg picture we have

(3)
(4)

with

(5)

Here |0〉 is the oscillator ground state, the α ±=α ±(0) are complex numbers encoding the initial position and velocity of the ion at t=0, and the \(\hat{a}_{\pm}^{\dagger}(0)\) are the creation operators for oscillator quanta at the initial time t=0. The amplitudes α ±(t) describe the motion of the center of the quasi-classical wave packet, which is characterized by the minimum uncertainty allowed by quantum mechanics, and which follows the trajectory predicted by classical mechanics.

The interconversion of the radial motional modes of an ion occurs due to its interaction with a quadrupolar rf-field

(6)

Expanding the spatial part with respect to α ± and \(\alpha_{\pm}^{\ast}\) we obtain

(7)

This decomposition has a straightforward interpretation in the quantum-mechanical context.

Inserting (7) into (6) and considering it as an operator equation (with α ± and \(\alpha_{\pm}^{\ast}\) replaced by annihilation operators \(\hat{a}_{\pm}\) and creation operators \(\hat{a}_{\pm}^{\dagger}\), respectively) the first term represents an interaction that is reducing or increasing the excitation of the cyclotron motional mode without changing the magnetron mode. The second term has an analogous interpretation, with the roles of the cyclotron and magnetron modes interchanged. Of greatest interest is the third term which describes the conversion of the magnetron into the cyclotron mode together with its inverse process. For example, converting the magnetron into the cyclotron mode from each absorbed photon of energy ħω exc an additional quantum of cyclotron motion with energy ħω + is created and one quantum of magnetron motion with energy −ħω − is annihilated. With ħω exc≈ħω ++ħω −=ħω c the interaction becomes resonant and dominates all others. This interpretation motivates our choice of the effective interaction for the interconversion of modes,

(8)

where c.c. is the complex conjugate. The coupling parameter g collects various constant factors including the trap geometry. Most importantly, it is proportional to the amplitude of the quadrupolar rf-excitation field.

It is interesting to translate the decomposition (7) back into cylindrical coordinates and velocities:

(9)
(10)
(11)

Inserting (11) and its complex conjugate into (8) we obtain a velocity-dependent classical interaction that would be difficult to motivate by classical arguments, but which appears very natural from the quantum-mechanical point of view. In the following we perform a thorough test of several aspects of this proposed effective interaction. On the other hand it should be emphasized that this treatment of the interconversion of motional modes is purely classical except for the motivation of the effective interaction.

The time development of the complex oscillator amplitudes during the interconversion process is described by the Hamiltonian

(12)

The equations of motion are complex linear differential equations

(13)
(14)

with the solution [5]

(15)
(16)

Here δ=ω exc−ω c denotes the detuning of the quadrupolar rf-field with respect to the resonance frequency ω c =ω ++ω −, and \(\omega_{R}=\sqrt{4g^{2}+ \delta^{2}}\) is the Rabi frequency of the interconversion.

For the interpretation of the experimental results it is useful to know that the instantaneous radii for the cyclotron and the magnetron motion, respectively, are given by

(17)

where 〈N ±(t)〉 denotes the expectation value for the number of quanta in the cyclotron and magnetron oscillators, respectively. An important property of the interaction (8) is the conservation of 〈N tot〉, the total number of oscillator quanta,

(18)

2.2 The one-pulse excitation scheme

Suppose we are performing a conversion experiment, starting at time t=0 with a state of pure magnetron motion, R +(0)=0, and R −(0)≠0. Then the conservation of 〈N tot〉 implies that throughout the conversion process \(R_{+}^{2}(t)+R_{-}^{2}(t) = R_{-}^{2}(0)\). The fraction \(n_{+}(t)=R_{+}^{2}(t)/R_{-}^{2}(0)=|\alpha_{+}(t)|^{2}/|\alpha_{-}(0)|^{2}\) varies between 0 and 1 and represents, when scanned with respect to the detuning δ, the one-pulse conversion profile F 1 given below.

Our solution (15) now provides an explicit expression for the conversion of pure magnetron motion into cyclotron motion after a pulse of quadrupolar excitation field has acted for a duration τ 1 with a detuning δ,

(19)

Experimentally this conversion profile can be obtained by plotting the square of the Fourier amplitude measured at the modified cyclotron frequency ν +=ω +/2π (i.e. the value of the power spectrum, not the magnitude spectrum usually studied by analytical FT-ICR MS) as a function of the detuning δ/2π. Starting with a state of pure magnetron motion (R +(0)=0, R −(0)≠0) and choosing ω exc=ω c (i.e. δ=0) a complete conversion of the initial state into cyclotron motion is reached after the ‘conversion time’ τ c =π/(2g). The ion is then in a pure cyclotron motional state. Afterwards reconversion to the magnetron state sets in and is complete after the ‘full Rabi period’ τ R =2τ c =π/g.

2.3 The two-pulse excitation scheme

In recent years a two-pulse excitation scheme (Ramsey method) has been developed in order to achieve higher precision [5, 23, 24]. As described above, for the complete conversion of a pure magnetron state (initial state) into a pure cyclotron state (final state) a pulse of quadrupolar excitation of duration τ c is necessary. For Ramsey excitation one applies two phase-coherent excitation pulses, each of duration τ 1=τ c /2, separated by a waiting period of duration τ 0. The amplitude has to be adjusted, accordingly. This scheme is illustrated in Fig. 1(b), in comparison with the conventional one-pulse excitation scheme in Fig. 1(a).

Fig. 1
figure 1

Schemes of (a) one-pulse quadrupolar excitation with an excitation time τ 1 and (b) two-pulse quadrupolar excitation. The two pulses of duration τ 1 each are separated by the waiting time τ 0. The total time is τ tot=2τ 1+τ 0

Full size image

The theoretical description of the Ramsey scheme requires an application of (15), (16) to each of the three intervals, setting g=0 during the waiting time, and carefully observing all phase relations. A detailed derivation can be found in Ref. [5]. The profile function for Ramsey excitation is obtained as

(20)

As in the former case the square of the Fourier transform magnitude, measured at the modified cyclotron frequency ν +, is obtained in the experiment in order to obtain the Ramsey conversion profile.

3 Experimental setup and the measurement method

3.1 Amplitudes of FT-ICR signals

The orbital motion of charged particles in the Penning trap results in time-varying image charges in the detection segments of the ring electrode. These are picked up as a function of time and the resulting transients are Fourier analyzed. As mentioned in the introduction, the ion motion in a Penning trap is characterized by three frequencies: The modified cyclotron frequency ν +, the magnetron frequency ν −, and the axial frequency ν z [4]. Possible signals are expected for each frequency combination n + ν ++n − ν −+n z ν z (n i positive or negative integer or 0). Using the computational method proposed by Grosshans et al. [27] it can be shown that the Fourier coefficient belonging to n + ν ++n − ν − is proportional to \((R_{+}/a)^{n_{+}}(R_{-}/a)^{n_{-}}\) (up to small corrections of order (R ±/a)2), where a denotes the radius of the cylindrical trap [28]. Thus, in leading order the Fourier amplitude for the signal at the modified cyclotron frequency ν + is proportional to R +. This proportionality is used for the interpretation of the experiments reported below.

3.2 Experimental setup and timing structure

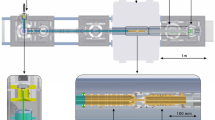
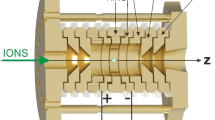
The experimental setup, shown in Fig. 2(a), has been built at the Max-Planck-Institut für Kernphysik (MPIK) in Heidelberg in order to test and commission a trap designed for the KArlsruhe TRItium Neutrino experiment (KATRIN) [29]. A detailed description can be found in Refs. [30, 31]. The trap is placed in an ultra-high vacuum system, i.e. p<5.0×10−9 mbar. A thermionic ion source delivers the lithium isotopes 6,7Li+ in natural abundances with a mean kinetic energy of 40 eV. The ions are focused by two electrostatic einzel lenses into a cylindrical Penning trap with open-endcap electrodes located at the center of the homogeneous 4.7-T magnetic field of a superconducting magnet. The Penning trap has two endcap electrodes and a ring electrode which were machined of copper and afterwards gold plated. The inner diameter of the electrodes is 71 mm and the total length is 260 mm. Figure 2(b) shows the configuration of the eight 45∘ segments of the ring electrode used for excitation (odd numbers) and detection (even numbers) of the ion motion. The image charges induced on the detection segments are picked up with two 2-channel broad-band low-noise preamplifiers mounted inside the vacuum on the Penning trap support structure. A broad-band post-amplifier mounted outside the vacuum cross is used for further amplification of the signals. The voltage-amplification factors of the pre- and post-amplifier were measured to be 6 and 60, respectively, in a frequency range from 1 to 30 MHz. The amplified signals are fed into a four-channel PCI-based transient recorder where the differential signal is calculated. A Fourier transformation delivers the magnitude-mode frequency spectra [33]. The timing structure for a measurement cycle is shown in Fig. 3. It consists of the following steps.

  1. (A)

    After injection, the ions are captured by applying the trapping potential to the endcaps. A waiting time of 10 ms is introduced for the cooling of the axial ion motion by collisions with rest-gas particles.

  2. (B)

    For all present studies, a resonant dipolar excitation field at the magnetron frequency is applied for a fixed excitation time of 7.5 ms. This causes a radial drift of the ion cloud out of the center of the Penning trap and defines the initial magnetron radius R −(0). The dipolar excitation field is generated by applying an AC signal with equal phase on the ring segments 1 and 3 (Fig. 2(b)) and with opposite phase on the ring segments 5 and 7. For the present cylindrical Penning trap [30], a trapping voltage U=55 V results in a magnetron frequency ν −=660 Hz.

    Fig. 2
    figure 2

    (a) Schematic view of the FT-ICR setup [30, 31]. The Penning trap is placed in a homogeneous region of the magnetic field. (b) Azimuthal view of the segmented ring electrode from the Penning trap used for excitation (not shown, odd numbers) and FT-ICR dipolar detection (even numbers). The signals are amplified by a preamplifier located inside the vacuum and a subsequent broad-band amplifier

    Full size image
    Fig. 3
    figure 3

    Timing structure for a measurement cycle. For details see text

    Full size image
  3. (C)

    A one-pulse or two-pulse quadrupolar excitation signal (Fig. 1) around the cyclotron frequency, ν c =ν ++ν −, of the ions is applied to convert the magnetron motion to the cyclotron motion [5, 32]. The quadrupolar excitation field is generated by applying an rf signal with equal phase on opposite ring segments 1 and 5 and an rf signal with opposite phase on the ring segments 3 and 7.

  4. (D)

    After the quadrupolar excitation the cyclotron motion is detected with the conventional FT-ICR dipolar method, which is performed by adding the two signals from the two detection segments 2 and 8 and subtracting the two signals from the detection segments 4 and 6. The resulting amplified dipolar signal is recorded for 100 ms with a sampling rate of 42 MHz and the magnitude-mode frequency spectrum is calculated, from which the Fourier amplitude at the eigenfrequency ν + is determined.

  5. (E)

    Finally, the ions are ejected toward a Faraday cup and the measurement cycle with a period of 390 ms starts again.

The Fourier amplitude measured at the modified cyclotron frequency ν + of 7Li+ spectra is proportional to the cyclotron radius and the number of ions [34, 35]. In all figures discussed below the FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{ exc}})\) is defined as the square of the measured Fourier amplitude at ν + in the magnitude-mode spectra. The excitation frequency ν exc is tuned in a range of ±500 Hz around the cyclotron frequency ν c by using a step size of 5 Hz. For each applied excitation frequency the measurement cycle is executed. The ion signal \(I_{\nu _{+}}(\nu_{\mathrm{ exc}})\) is directly correlated with the conversion of pure magnetron into cyclotron motion, as expressed by the conversion profile functions given in (19) and (20). These conversion profile functions are fit to the data by use of the Levenberg–Marquardt method [36], a standard technique for least squares curve-fitting problems. The error bar was determined as 5% variation of the Fourier amplitude at the modified cyclotron frequency in the magnitude-mode spectra. We assumed the same error bar for each data point.

4 Results and discussion

The FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{ exc}})\) has been studied for the conventional one-pulse and the two-pulse quadrupolar excitation schemes for 7Li+ ions. Regarding the one-pulse excitation scheme, the coupling of the ions with a quadrupolar field is investigated for different rf-excitation amplitudes U exc, which allows a determination of the conversion time τ c . Furthermore \(I_{\nu _{+}}(\nu_{\mathrm{ exc}})\) is measured as a function of the excitation time τ 1. For the two-pulse Ramsey excitation, parameters such as the waiting time τ 0 and the excitation time τ 1 are changed. These measurements illustrate the influence of each parameter on the interaction of the ion with both excitation fields. Finally, the theoretical predictions are compared with the data.

4.1 One-pulse excitation: variation of rf-excitation amplitude

The strength of the coupling of a quadrupolar field to the ions is defined by the coupling constant g, which is inversely proportional to the conversion time. It is observed that the conversion time gets shorter if the strength of the driving field to the ions is stronger: Fig. 4 shows the conversion time τ c as a function of the rf-excitation amplitude at a constant excitation time τ 1=9.2 ms. The fit of the one-pulse profile function F 1 to the data (details below) gives the coupling constant g and thus the conversion time τ c =π/(2g). As expected, the conversion time is inversely proportional to the rf amplitude. A larger coupling due to an increased excitation field strength and thus a larger radial force leads to a faster conversion rate between the radial motional modes.

Fig. 4
figure 4

Experimental conversion time τ c as a function of the rf-excitation amplitude U exc,PP, obtained from the coupling constant g=π/(2τ c ). The solid line is a fit to the data

Full size image

Figure 5 shows the FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{ exc}})\) as a function of the detuning ν exc−ν c for three different rf amplitudes, namely U exc,PP=1.7 V (a), 3.4 V (b) and 5.0 V (c) for a constant excitation time τ 1=9.2 ms. Each data point corresponds to one excitation frequency. In general, the rf amplitude can be chosen such that the excitation time is equal (2n+1)τ c (n integer). In this case the ions are converted to purely cyclotron motion and the FT-ICR ion signal shows the largest intensity with the dipolar-detection method [27], as in panel (a) and (c). Comparison of these two spectra shows that the line-width increases with larger rf amplitudes due to a larger coupling strength of the ions to the quadrupolar rf-field. This effect can be explained by considering the one-pulse profile function F 1 (see (19)). The phase of the sinusoidal function, ϕ=ω R τ 1/2, depends on the Rabi frequency ω R of interconversion and shows a nonlinear behavior in the detuning δ=2π(ν exc−ν c ). The derivative of the phase with respect to the detuning, dϕ/dδ=τ 1 δ/ω R measures the slope of the nonlinear phase. It is observed that the larger the coupling constant g the smoother increases the slope of the derivative around the detuning δ=0. Thus a broadening of the line-width of the central peak is observed. The line-width reduction with decreasing g is analogous. Additionally, in the special case when the detuning is much larger than the rf amplitude, i.e. δ≫g, the slope of the derivative depends mainly on the excitation time τ 1. The profile function is then approximately the Fourier transform of a scalar wave train since the sinusoidal oscillations are independent of g.

Fig. 5
figure 5

Experimental 7Li+ FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{ exc}})\) for one-pulse quadrupolar excitation with three different rf-excitation amplitudes U exc,PP=1.7 V (a), 3.4 V (b) and 5.0 V (c) for a constant pulse duration τ 1=9.2 ms as a function of the detuning ν exc−ν c . The solid lines are fits of the theoretical one-pulse profile function F 1 (see (19))

Full size image

Figures 5(a) and 5(c) also reveal different intensities of the fringes depending on the rf amplitude, which are described by the prefactor 4g 2/(4g 2+δ 2) of the one-pulse profile function. The prefactor increases if the coupling constant g is increased. As long as 2g>δ the intensity of the fringes are more pronounced.

Figure 5(b) shows the FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{ exc}})\) for an rf amplitude of 3.4 V where the excitation time τ 1=9.2 ms is roughly two times the conversion time. The ions are converted back to the initial magnetron radius, i.e. the FT-ICR signal at detuning δ=0 Hz vanishes.

Figure 6(a) shows the measured FT-ICR signal intensity and Fig. 6(b) is the expected function F 1 in a color-coded contour plot as a function of the detuning and rf amplitude. Since the coupling constant behaves linearly with the rf amplitude, the theoretical function is shown in units of the coupling constant. In Fig. 6 we observe up to three successive conversions from the magnetron motion to the cyclotron motion. The effect of line-width broadening for larger rf amplitudes appears due to the larger coupling strength of the quadrupolar rf-field to the ions. The theoretical predictions and the experimental data agree very well.

Fig. 6
figure 6

One-pulse quadrupolar excitation: (a) the square of the experimental FT-ICR amplitude as a function of the excitation amplitude U exc,PP and the detuning δ; (b) contour plot of the theoretical profile function for one-pulse quadrupolar excitation as a function of the coupling constant g and the detuning δ

Full size image

4.2 One-pulse excitation: variation of excitation time τ 1

Next we present the one-pulse quadrupolar-excitation results for different excitation times τ 1 by using a rf-excitation amplitude of 5.0 V. Figure 7 shows the experimental FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{ exc}})\) with theoretical fits (solid line) for excitation times of τ 1=3.2 ms (a), 6.13 ms (b) and 9.24 ms (c), which correspond to one, two and three times the conversion time τ c : For δ=0 a pulse duration of τ c (a) leads to a conversion to pure cyclotron motion. After a pulse duration of 2τ c (b) a back conversion from the cyclotron to the magnetron motion at the measured cyclotron frequency is observed. Again after τ 1=3τ c (c) only the cyclotron motion occurs, as expected from theory.

Fig. 7
figure 7

Experimental FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{exc}})\) for one-pulse quadrupolar excitation for three different pulse durations τ 1= 3.2 ms (a), 6.13 ms (b) and 9.24 ms (c) with a constant rf-excitation amplitude U exc,PP=5.0 V as a function of the detuning ν exc−ν c . The solid lines are fits of the theoretical one-pulse profile function F 1 (see (19))

Full size image

The intensity of the fringes increases with longer excitation times as expected when considering the zeros of the profile function F 1: For an excitation time of τ 1=(2n+1)τ c (full conversion to only cyclotron motion) the position of the zeros of F 1 next to the central peak are given by \(\delta_{0} /(2\pi)=\pm\sqrt{4n+3}/((2n+1)2\tau_{c})\). This equation implies that in terms of frequencies the detuning δ 0 at the position of the first zero obeys a sort of time-energy uncertainty relation: \(\hbar \delta_{0} \cdot\tau_{c} (2n+1)= h\sqrt{4n+3}/2\). The longer the excitation time the more conversions are occurring while the line-width of the central peak shrinks. In consequence, the intensities of the nth-order fringes are influenced because the Rabi oscillation gets slower if δ 0 shrinks. It follows that the prefactor 4g 2/(4g 2+δ 2) of the one-pulse profile function F 1 will increase and thus so will the intensity of the fringes.

Figure 8 shows \(I_{\nu_{+}}\) as a function of the detuning and the excitation time in a color-coded contour plot. During an excitation time of 18 ms three full conversions to cyclotron motion happen at δ=ν exc−ν c ≈0 Hz. For a larger detuning more conversions are performed. Thus, the frequency of interconversion, the Rabi frequency, increases. However, as explained above, the ion motion is converted for a non-zero detuning from a pure magnetron motion into a mixed motional mode, only.

Fig. 8
figure 8

One-pulse quadrupolar excitation: (a) the square of the experimental FT-ICR amplitude as a function of the excitation time τ 1 and the detuning δ; (b) contour plot of the theoretical profile for one-pulse quadrupolar excitation for the same parameters τ 1 and δ

Full size image

4.3 Two-pulse (Ramsey) excitation: variation of waiting time τ 0

In this section we show some results for the two-pulse Ramsey excitation scheme. Figure 9 shows the FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{ exc}})\) for constant excitation time τ 1=3.4 ms at three different waiting times τ 0= 6.8 ms (a), 17.0 ms (b) and 23.8 ms (c). The excitation time of the first excitation pulse corresponds to half of the conversion time. For resonant excitation at ν c =ν ++ν − in all three cases a full conversion to cyclotron motion occurs. In addition, the envelopes are the same for different waiting times. It is described by a one-pulse profile function, which appears in (20) as the first sin2(ω R τ 1/2)-term. As expected from the theory section, more fringes appear around the center peak for longer waiting times and thus the width of the center peak gets narrower. This effect is observed by rewriting the two-pulse profile function into

(21)

The oscillations are specified by the \(\cos^{2}(\frac{\delta\tau_{0}}{2} )\)-term with respect to the detuning for a constant waiting time. The distance between the zeros is approximately given by Δδ⋅τ 0/2=π, i.e. Δν=1/τ 0. Thus the ion motion is converted back to the magnetron mode at many excitation frequencies ν exc around the resonance frequency.

Fig. 9
figure 9

Experimental FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{exc}})\) for two-pulse Ramsey excitation for three different waiting times τ 0=6.8 ms (a), 17.0 ms (b) and 23.8 ms (c) with a constant pulse duration τ 1=3.4 ms and constant rf amplitude U exc,PP=2.9 V as a function of the detuning ν exc−ν c . The solid lines are fits of the theoretical two-pulse profile function F 2 (see (20))

Full size image

After the first excitation pulse the ion motion is a superposition of the magnetron and cyclotron motion. The radii of both motions are equal if the driving frequency ν exc hits the resonance frequency. For an off-resonant excitation, ν exc≠ν c , there is less conversion and thus the magnetron radius is larger than the cyclotron radius after the first excitation pulse. Note that both excitation pulses are phase locked. Therefore, if there is a detuning, the conversion of magnetron into cyclotron motion remains incomplete after the second excitation pulse. In that case the cyclotron motion is superimposed by a magnetron motion. The increase of the waiting time influences the resolving power due to the increase of the total time τ tot=2τ 1+τ 0.

Additionally, Fig. 9(c) shows that the ion motion is converted almost completely into cyclotron motion at the first fringe at ν exc≈±36 Hz beside the center peak. In Ref. [5] it is shown that the condition (δ/2g)2≤1 should be fulfilled, which means in our case |(ν ext−ν c )|≤63 Hz for an rf amplitude of U ext,PP=2.9 V (g≈198 Hz). As described above, the distance between the fringes decreases with increasing waiting time.

Figure 10 shows, similar to Fig. 6 and Fig. 8, \(I_{\nu_{+}}\) as a function of the waiting time τ 0 and the detuning δ. The prediction agrees well with the experimental results. The intensity of the central fringe and the nth-order fringes decrease due to collisions with rest gas particles. The collisions lead to a decrease of the cyclotron radius and randomization of the phase of the cyclotron motion. Additional mechanisms like ion-ion interactions as well as trap anharmonicity lead to further dephasing of the ion cloud [37, 38].

Fig. 10
figure 10

Two-pulse Ramsey excitation: (a) the square of the experimental FT-ICR amplitude as a function of the waiting time τ 0 and the detuning δ. (b) Theoretical contour profile for two-pulse Ramsey excitation for the same parameters τ 0 and δ

Full size image

4.4 Two-pulse (Ramsey) excitation: variation of excitation time τ 1

The interaction of the ions with the two-pulse quadrupolar field was further studied by varying the excitation time τ 1 with a constant waiting time τ 0=7.5 ms between the two pulses. Figure 11 shows the FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{ exc}})\) for three different excitation times. The conversion time τ c is roughly 7.5 ms so that panel (a) and (c) show complete conversions from the magnetron mode to the cyclotron mode after the two resonant pulses with a duration of 2τ 1=τ c and 2τ 1=3τ c , respectively. In panel (b) a back conversion to the magnetron motion occurs after 2τ 1=2τ c of resonant excitation.

Fig. 11
figure 11

Experimental FT-ICR signal intensity \(I_{\nu_{+}}(\nu_{\mathrm{exc}})\) for two-pulse Ramsey excitation for three different excitation times τ 1=4 ms (a), 8 ms (b) and 11 ms (c) with a constant waiting time τ 0=7.5 ms as a function of the detuning ν exc−ν c . The rf amplitude was U exc,PP=2.9 V. The solid lines are fits of the theoretical two-pulse profile function F 2 (see (20))

Full size image

Figure 12 shows the comparison of the data and the two pulse profile function as a function of the excitation time and the detuning in color-coded contour plots. A full conversion to cyclotron motion occurs at a excitation time of 4 ms and 11 ms. For the larger excitation time the line-width of the central peak is increased (compare also panel (a) and (c) in Fig. 11). The narrowest line-width reappears periodically at excitation times 2τ 1=(4n+1)τ c , with n=0,1,2,3,… . This equation shows that the reconversion to the cyclotron motion occurs periodically with the Rabi period τ R =2τ c =4τ 1. In our case the Rabi period is τ R =15 ms. The larger line-width of the central peak occurs periodically after 2τ 1=(4n+3)τ c . In the latter case the first zeros next to the central peak are described by the sin2(ω R τ 1/2)-term in front of the two-pulse profile function (see (21)) because the term \([1-\frac{\delta }{\omega_{R}}\tan (\frac{\delta\tau_{0}}{2} )\tan (\frac {\omega_{R}\tau_{1}}{2} ) ]^{2}\) does not have an extra zero.

Fig. 12
figure 12

Two-pulse Ramsey excitation: (a) the square of the experimental FT-ICR amplitude as a function of the excitation time τ 1 and the detuning δ; (b) theoretical contour profile for two-pulse Ramsey excitation for the same parameters τ 1 and δ

Full size image

In order to study the interaction between the ions and two-pulse quadrupolar field for a constant total τ tot=2τ 1+τ 0=15 ms time, we also performed measurements for varying ratios τ 1/τ 0 at a constant rf amplitude (not shown). We observed that the line-width of the central peak decreases with increasing waiting time.

5 Conclusions

Experimental and theoretical investigations of the interaction of ions with one- and two-pulse (Ramsey) quadrupolar excitation fields are presented. The interpretation of the interconversion of radial motional modes is motivated by the quantum-mechanical description of the response of the ion to the quadrupolar fields. The classical amplitudes of the radial ion motions are derived as expectation values of the creation and annihilation operators in the quasi-classical coherent state. The FT-ICR dipolar-detection method is used to measure the Fourier amplitude at the modified cyclotron frequency ν + for detecting the cyclotron motion of 7Li+ ions. We investigated important parameters such as excitation time τ 1, waiting time τ 0 and rf-excitation amplitude U exc, to observe the effects on the interconversion spectrum (i.e. intensity versus detuning) of pure magnetron motion into cyclotron motion. The one-pulse excitation scheme shows the narrowest line-width of the center peak, when the excitation time τ 1 is equal the conversion time τ c . Therefore, a long conversion time due to a weak coupling constant results in an increase of the resolution power as expected from the time-energy uncertainty relation. A narrower line-width of the center peak is achieved by increasing the pulse duration from τ 1=1τ c to τ 1=nτ c with n=2,3,4,… .

For the two-pulse Ramsey excitation scheme of excitation time 2τ 1=τ c , i.e. the duration of the pulses is equal to half the conversion time, the number of fringes near the center peak increases with the waiting time τ 0. This effect improves the statistical uncertainty in high-precision mass spectrometry. The reduction of the line-width of the central peak leads to a gain in precision of measured value of the resonance frequency. In addition, as expected from theory, the ion motion for off-resonance excitation is converted to a pure cyclotron motion if the waiting time is long enough and the interaction for the interconversion of modes is strong. For both excitation schemes the theoretical FT-ICR profile functions agree very well with the data.