Regression based computer vision analysis of volume-fraction effect on Pb–Sn solid–liquid coarsening in microgravity

Abstract

Outcomes of coarsening experiments performed in solid–liquid mixture of various Pb–Sn systems, under microgravity, are investigated to explicate the influence of volume fraction on coarsening kinetics. A computer vision technique capable of efficiently ascertaining the number of Sn-rich solid precipitate is developed. After sufficient training and validation, this object detection model is employed to micrographs of Pb–Sn systems captured at different stages of coarsening. The change in the number density of the precipitate with time is monitored for different Pb–Sn systems of varying phase fractions, ranging from 5 to 80% precipitates, and the corresponding kinetics coefficient is determined using regression. Examining the kinetic coefficients in relation to phase fractions unravels that the volume of Sn-rich solid has negligible effect on the steady-state coarsening rate of the Pb–Sn solid–liquid mixture under microgravity. The indefinite and marginal effect of precipitate volume-fraction on kinetic coefficient apparently substantiates the trans-interface diffusion governed coarsening in Pb–Sn system, as opposed to generally held dominance of matrix diffusion.

1 Introduction

Technological advancements demand materials with combination of properties which are generally deemed irreconcilable [1, 2]. The need in the automotive industries for alloys with extremely highly strength and ductility is one of the prime example [3]. Materials with multiple phases are developed to cater to these demands. Largely employed multiphase materials often comprise of two phases, which are referred to as the matrix and precipitate depending on their distribution. The behaviour of the two-phase system, in a given environment, depends on the size and distribution of the precipitates in the matrix [4]. Therefore, in order to achieve desired properties, the corresponding materials are suitably heat-treated so as to establish the required size and distribution of the phases [5]. The heat-treatment cycle associated with this processing is rather straightforward, and is characterised by holding the material at high temperature without introducing any phase transformation [6]. This isothermal treatment offers the necessary conditions for the two-phase system to reduce its overall-energy by decreasing the ‘high energy’ interfacial area separating precipitate and matrix. In other words, the heat treatment induces coarsening wherein larger particles grow at the expense of the smaller ones thereby increasing the average size of the precipitates and ultimately, reducing the interfacial energy per unit volume.

The mechanism undergirding coarsening is rather well-understood. In a two-phase system characterised by precipitates with wide-range of sizes, the equilibrium concentration, bolstering the phase-fraction, varies at the interface depending on the curvature [7]. Consequently, a gradient in the solute concentration is introduced in the binary material, thereby inducing mass transfer (diffusion), that establishes coarsening. Founded on this understanding, several theoretical models have been developed to essentially optimise the processing technique associated with coarsening [8, 9]. Pioneering investigations on coarsening are separately reported by Lifshitz and Slyozov [10], and Wagner [11], which collectively renders the seminal LSW theory. The corresponding analyses focusing on two-phase materials with phase-fraction dominated by matrix, and precipitates restricted to the traces, claim that the evolution accompanying coarsening attains a steady state after sufficient duration. The steady-state evolution is evident in two principal microstructural changes typifying coarsening. These principal changes include a progressive increase in the average radius and decrease in the number of precipitates. According to the LSW theory, under steady-state coarsening, the change in the average radius of the precipitate follows

$$\begin{aligned}<r(t)>^3 - <r_0>^3 = kt, \end{aligned}$$

(1)

where $<r_0>$ and $<r(t)>$ correspond to the average radius of the precipitates at initial condition ($t=0$) and at time, t. In above relation, rate constant k dictates the kinetics of coarsening. Besides the average radius, the change in the number of precipitates, resulting from the evanescence of the relatively smaller particles, during the steady-state coarsening is expressed as

$$\begin{aligned} N_v(t)=k_Nt^{-1}, \end{aligned}$$

(2)

where $k_N$ dictates the rate of change in the number of precipitates while $N_v(t)$ captures the particle number-density at a given instant.

Owing to its claims on the kinetics of coarsening, several experimental observations have been analysed in view of the LSW theory to assess its accuracy and extend its applicability [12,13,14]. However, a general lack of a binary two-phase system that fits-in with the LSW framework poses a huge limitation to these investigations. In other words, beside the specific condition on phase-fraction, the LSW theory is developed under the assumption of isotropic interfacial energy, which is independent of the crystallographic directions, thereby favouring precipitates of spherical morphology [15]. Additionally, the LSW predictions, in Eqs. (1) and  (2), overlook the role of any inelastic eigenstresses between the precipitate and the matrix [16]. Two-phase systems, particularly solid-state ones, adhering to the above assumptions are extremely rare. Therefore, given the general absence of stress in matrix, coarsening studies have been extended to solid–liquid systems with isotropic interfacial energies.

Pioneering investigations of coarsening in solid–liquid mixture focus on copper–cobalt (Cu–Co) system [17, 18]. Besides the stress-free matrix, the choice of this system is vindicated by isopycnic nature of the constituent phases. Stated differently, the almost identical density of the solid and liquid phase in Cu–Co system precludes any sedimentation, and other associated unsought effects. Despite rendering a seemingly ideal setup for examining coarsening, the high temperature required to establish the solid–liquid mixture in Cu–Co system has not been favourably perceived. Consequently, subsequent studies primarily involve lead–tin (Pb–Sn) system wherein the desired solid–liquid mixture can be established at much lower temperature [19, 20]. However, unlike Cu–Co, the densities of the phases in Pb–Sn system are noticeably different, thus introducing sedimentation of the Sn-rich solid precipitates. This inadmissible evolution in the solid–liquid mixture is counteracted by inducing coarsening under significant absence of gravity.

Coarsening in Solid–Liquid Mixture (CSLM) of Pb–Sn system is one of early investigations performed under microgravity [21]. The microstructural changes accompanying Pb–Sn coarsening have been examined in Microgravity Science Laboratory of the Space Shuttle Columbia and Microgravity Science Glovebox abroad the International Space Station (ISS). Several Pb–Sn systems that render varying phase-fractions, id est volume fractions of Sn-rich solid, are allowed to coarsen in the environment of negligible gravity. The outcome of these studies, gathered as micrographs at different timespans for each volume fraction, have been achieved and made accessible to the researchers through the Physical Science Informatics portal of National Aeronautics and Space Administration [22].

In addition to preventing sedimentation of the solid precipitates in the Pb–Sn system, coarsening in microgravity inhibits any buoyancy-induced convections. Put differently, solid–liquid mixture of Pb–Sn, owing to its inherent features, in the absence of gravity presents itself as an ideal system for a comparative investigation of the LSW theory. To that end, outcomes of CSLM in Pb–Sn systems, in the absence of gravity, have primarily been investigated in view of LSW theory [21, 23]. In keeping with the presumed strategy, these studies unravel that the coarsening kinetics exhibited by Pb–Sn systems, despite the relatively higher volume fractions, adhere to the LSW predictions.

Though the existing analyses substantiate the fundamental claims of the LSW theory involving the change in the average radius and number of precipitate, a convincing understanding is yet to be gained on the influence of volume fraction. Considering that an increase in the volume fraction of the precipitate consequently reduces the length of the diffusion path in the matrix, an increase in the coarsening kinetics is reasonably postulated, and has been seemingly corroborated in the early investigations [21, 24]. However, a recent report indicates a marginal and indefinite effect of volume fraction on the coarsening rate in Pb–Sn system under microgravity [25]. Moreover, the negligible influence of volume fraction is attributed to the trans-interface-diffusion-controlled (TIDC) coarsening, wherein the solute transfer across the diffuse interface, established between the precipitate and matrix, is sluggish and primarily dictates the kinetics, as opposed matrix diffusion [26]. Owing to the direct contraction in existing perception of the influence of volume fraction ($k_N (f_e)$), kinetics of coarsening in several Pb–Sn system with phase-fraction ranging from 5 to 80% precipitate is analysed in the present study. To capture the coarsening rate, this study exclusively focuses on the change in the number density of the precipitate ($N_v(t)$). The number of precipitates in the micrograph, at a given time, is estimated by employing object-detecting computer vision technique.

2 Data and technique

Though the principal focus of the present work is to analyse coarsening exhibited by Pb–Sn system in microgravity, this is pursued by monitoring the corresponding evolution through a machine-learning algorithm that undergirds the adopted computer vision technique. Accordingly, the ensuing investigation can be viewed as a data analysis, wherein instead of conventional numerical entities, micrographs from the shuttle and ISS experiments are handled as the data.

2.1 Experimental setup

Existing works [21, 23], and other dedicated reports [22], extensively discuss the experimental techniques associated with the CSLM studies of Pb–Sn system under microgravity. Nevertheless, the relevant aspects of these experiments are succinctly presented in this section.

Ingots of different Pb–Sn alloys with characteristic volume fraction of solid Sn are fabricated by casting in a steel mold. These ingots are subsequently transformed, through cold working and machining, into solid cylinders of dimensions 1 cm and 6 cm in diameter and in height, respectively. The dimensions ensure the stable positioning of the samples in the furnace holders. The samples and the holding furnace are placed in the microgravity lab/glovebox and are heated to a temperature of $185^\circ$C. This temperature, which is $2^\circ$C above the eutectic temperature of Pb–Sn system, facilitates melting and ultimate formation of solid–liquid mixture with Sn-rich particles suspended in Pb–Sn liquid. The volume fraction of the precipitate reflects the initial alloy composition of the ingot. Owing to the isotropic energy condition, the Sn-rich precipitate assumes a spherical shape. The samples are held at $185^\circ$C for a predetermined duration of time, after which they are quenched with water. Considering that the room temperature is relatively high for Pb–Sn system, the samples after quenching are stored at low-temperature ($-80^\circ$C) to avoid any further coarsening. Once back on earth, these samples are sectioned and characterised. The micrographs reflecting the progressive coarsening of the various Pb–Sn systems are made available in [22], which is exploited for the present investigation.

2.2 Object detection technique

Though the PSI portal of NASA grants access to the micrographs of the Pb–Sn system during coarsening, the relevant information to estimate the kinetics, including the change in the average radius, does not accompany the corresponding database. Therefore, a recent work adopts an online tool to digitise the micrographs and extract the necessary information to ascertain the kinetics [25]. Such acquisition of data are generally laborious, and the accuracy of the rendered information cannot be definitively argued On the other hand, the present work extends an object-detection technique to count the number of precipitates in a micrograph [27]. Besides reducing human efforts, the accuracy of this established model can be inherently quantified from its training and validation.

Though originally intended to aide in day-to-day activities, ranging from surveying to traffic control, object detection, like several other computer vision techniques, has successfully been inducted into technical investigations [28]. These and other computer vision models are increasingly employed in materials research, particularly to deepen the perception of the experimentally-observed microstructures [29, 30].

A conventional object detection algorithm comprises of two principal steps [31]. One, a given image is assessed using sliding windows of varying sizes to capture the sections with distinct patterns. These sections, in step two, are classified based on the recognised pattern using appropriate schemes like Convolution Neural Network (CNN). In order to achieve an accurate detection, these steps are sequentially iterated. Owing to the inherent nature of the algorithm, which demands numerous repetition of pattern recognition and classification, the agility of the corresponding object detection approach is rather deficient, and its computationally expensive. The technique adopted in the present investigation, on the other hand, circumvents the taxing iteration of recognition and classification, by detecting the objects through regression. Stated otherwise, instead of examining various local sections of an image, the current scheme takes a global view and predicts the presence of the objects. Owing to its characteristic structure of the algorithm, the current technique is aptly referred to as YOLO, You-Only-Look-Once [32].

Object detection in YOLO is initiated by discretisation of the image into identical M $\times$ M grids (or cells). Assuming that each grid is the center of the object, the algorithm predicts a bounding box that encapsulates the corresponding object. Consequently, the cells constituting the image are associated with four parameters, $\{b_x,b_y, b_w,b_h\}$, with $b_w$ and $b_h$ indicating the dimensions of the bounding box, while $b_x$ and $b_y$ denoting its center. Even though all four parameters are collectively expressed, the center of the box ($b_x$ and $b_y$) is described with respect to the individual grids, whereas the dimension relate to the entire image. Furthermore, the confidence of finding an object within a predicted bounding box is estimated, based on the ground truth, as

$$\begin{aligned} \mathcal {C}=\mathcal {P}\,(\text {ob})\times IoU, \end{aligned}$$

(3)

where $\mathcal {P}(\text {ob})$ is the probability of locating an object within the predicted box. In Eq. (3), the overlap between the predicted bounding box and the ground truth is represented by Intersection of Union, IoU. When an object is absent in a bounding box, the respective cell would be distinguished by null confidence, $\mathcal {C}=0$. The confidence ascertained using Eq. (3) for each grid will be appended to the existing set of parameters that indicate the center and dimensions of the predicted box. When an image comprises of more than one class of object, the probability of finding the individual classes in a bounding box are estimated ($\mathcal {C}_i=\mathcal {P}(\text {cl}_i|\text {ob})\times \mathcal {P}(\text {ob})\times IoU$), and are separately associated with each cell. However, since the micrographs analysed in the present work comprise of a single class of object, precipitates, ascertaining class probabilities become redundant. Of the several different boxes predicted by the algorithm, the most accurate ones are realised principally based on the confidence ($\mathcal {C}$) by using non-max suppression scheme.

The undergirding object detection algorithm of YOLO, by its discretisation and prediction, translates a given image with a single object-class into a third order tensor of dimension [$S\times S\times (B\times 5)$], where B indicates the total number of bounding boxes ultimately realised. Moreover, a predicted bounding box is expressed as a vector

$$\begin{aligned} {\varvec{\hat{y}}}= \begin{bmatrix} \mathcal {C}\\ b_x\\ b_y\\ b_w\\ b_h \end{bmatrix}, \end{aligned}$$

(4)

for a single-class image. This vector representation of the predicted box is compared with the similar representation of the ground truth (${\varvec{y}}$) during training to enhance the accuracy of the prediction. The size of the bounding-box vector increases with addition of different classes of objects.

Fig. 1

A schematic representation of the approach adopted to involve a computer vision technique for counting number of precipitates in a micrograph (Micrographs included in the representation are part of the open database in [22])

Despite the rather recent conception of the YOLO object-detection technique, several advancements in the form of different versions have been reported [33, 34]. These improvements, which ultimately enhances the efficiency and accuracy of the approach, includes introduction and optimal usage of anchor box, involvement of adept activation function in the underlying networks, and data enhancement. In the present work, the latest version of this technique with the updated features, YOLOv5, is employed to detect and count the precipitates in the micrographs. Recently, this object detection technique has been extended to realise the topological features of individual grains in polycrystalline systems [35].

2.3 Precipitate counting

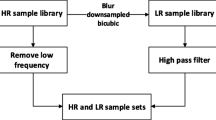
The approach adopted in the present work to extend an object detection algorithm for identifying and counting the precipitates in the micrographs is schematically represented in Fig. 1. From the principal dataset of micrographs offered by the PSI-NASA[22], a sample data of 100 microstructures are randomly extracted. Consequently, the sample data comprises of microstructures with varying volume fractions of solid precipitates at different stages of coarsening. A portion of the sample data, close to $80\%$, is used to train the model.

In the present framework, training of the model involves manually introducing bounding boxes around the precipitates in all of the micrographs pertaining to the training data. These manually introduced bounding boxed, during the development of the model, serve as the ground truth. The manual labelling is performed on a digital platform, makesense.ai, which converts a bounding box to its respective vector, as expressed in Eq. (4). subsequently, a machine-readable text file comprising of arrays of the vectors, that encompasses bounding boxes encapsulating all the precipitates in the micrograph, is generated. After sufficient training, the model is validated against the remnant micrographs ($20\%$) of the sample data. The performance of the model, during validation, is further enhanced by fine-tuning the hyperparameters. Besides accurately detecting and locating the precipitates, the trained and validated model counts the number of objects thereby tracking the changes in the number density with time.

2.4 Model performance

Fig. 2

a Change in the box and object loss with increase in epoch during training and validation. b Precision and recall curve indicating the accuracy of the model in detecting the precipitates in a micrograph

Unlike image analysis treatment, which do not offer sufficient information of it accuracy, the performance of the present computer vision technique can be convincingly described. For 200 epochs and batch size of 4, the metrics delineating the performance of the present object-detection approach is shown in Fig. 2. Other hyperparameters including learning rate, momentum and weight decay assume a value of 0.01, 0.937 and 0.0005, respectively. The deviation of the model prediction from the ground truth is estimated as loss, and its change with number of epochs is illustrated in Fig. 2a [36]. A lower loss indicates a higher accuracy of the model. In other words, when there is a significant overlap between the predictions of the object detection model and ground truth, the corresponding loss would be minimal. Therefore, loss is deemed as one of the primary metric for assessing the performance of the model.

In Fig. 2a, the variation in two different losses, during training and validation, are illustrated. The box loss quantifies the disparity between the bounding boxes predicted by the model, and the ground truth. The disparity is determined from the CIoU which considers Intersection of Union (IoU), centers, dimensions and aspect-ratios of the predicted and actual (ground truth) bounding box. The deviation, which translates to box loss, can be equivalently calculated from the entries of the bounding box vector, Eq. (4), pertaining to the prediction and the ground truth. It is evident from Fig. 2a, during both testing and validation, the box loss significantly decreases with increase in epoch ($\mathcal {E}$), and attains a negligible value at $\mathcal {E}=200$, thereby identifying a hyperparameter for optimal performance. The object loss included in Fig. 2b depicts the ability of the model to distinguish precipitate (object) from the matrix. The accuracy of the model to realise the precipitate is ascertained from binary cross entropy, which reflects the probabilities of the predictions. Similar to the box loss, for the present model and its corresponding parameters, the object loss assumes a minimal value, thereby affirming the accuracy in detecting the precipitates.

Besides the loss functions, which largely indicate the disparity between the predictions and ground truth, the performance of the model can also be described based on its precision. The prediction made by the object detection model can be categorised as true positive (TP), false positive (FP) and false negative. In the present case, true positive indicates the accurate detection of the precipitate by the technique while overlooking the matrix. On the hand, labelling a section of matrix as precipitate constitutes a false positive, while false negative is the failure of the model to detect a precipitate, by deeming it to be matrix. In order to describe the performance of the technique based on the nature of its predictions, two parameters are calculated as

$$\begin{aligned} {P}=~\frac{\text {TP}}{{\text {TP}} + {\text {FP}}}\quad \text {and} \quad {R}=~\frac{\text {TP}}{{\text {TP}} + {\text {FN}}}, \end{aligned}$$

(5)

where P and R refer to precision and recall, respectively. During the development of the present object detection model, the precision and recall are estimated and a PR curve is plotted. The maximum area which can be enclosed by the PR curve is 1.0, and it indicates a complete absence of false positives and false negative. Stated otherwise, the average precision (AP) of the model, which refers to the area under the PR curve, reflects the accuracy of the predictions. While the mean-average precision (mAP) is introduced to delineate the accuracy in images with several object-classes, in the present investigation, wherein precipitates are the only object, it is equivalent to the average precision. The PR curve rendered by the current technique is shown in Fig. 2b. The average precision of the developed object-detecting approach, ascertained from the area under the PR curve, is extremely close to the ideal value, AP = 0.992, indicating the high fidelity of the predictions.

Fig. 3

To substantiate the accuracy of the object detection model, the manually labelled micrographs of $10\%$ and $80\%$ solid fraction, at time 14,400 s and 36,600 s, are compared with the respective processed outcomes (Micrographs included in the representation are part of the open database in [22])

3 Results and discussion

3.1 Comparison with manual labelling

Even though the performance of the object detection approach is discussed using the inherent metrics in Sect. 2.4, given its pivotal role in the present investigation, the accuracy of the technique is further analysed by examining manually labelled and machine-detected micrographs together. To that end, two micrographs of Pb–Sn systems with precipitate volume-fraction of $10\%$ and $80\%$ at time 14,400 s and 36,600 s, respectively, are randomly selected. Figure 3 shows the precipitates of these micrographs detected manually and through the present computer vision model. When viewed comparatively, there exists an absolute agreement between the detection made by the human faculties and the technique. Put differently, Fig. 3 asserts the ability of the the present approach to identify, and thereby accurately count, precipitates in micrographs where they are both scarcely ($10\%$) and densely populated ($80\%$).

3.2 Coalescence of precipitates

Fig. 4

Combination of object detection and segmentation ensure the reasonable accuracy of the estimated average radius (Micrographs included in the representation are part of the open database in [22])

Besides facilitating the growth of larger particles at the expense of smaller one, the system further reduces its interfacial energy per unit volume through the coalescence of the precipitate, wherein two particles fuse to form a single mass [37]. In-keeping with its description, coalescence between particles is deemed complete only when the original boundaries separating these precipitates totally disappear. The dissipation of the boundaries during coalescence ultimately reduces the interfacial area locally. Coalescence of precipitates during coarsening is not uncommon. Particularly, when the volume fraction of the precipitate is significantly higher, thereby considerably decreasing the distance separating the precipitates, coarsening is generally accompanied by coalescence. Therefore, the present model is appropriately trained to distinguish coalesced particles from the precipitates which are contact with one another. In other words, the model detects the ‘coalescing’ particles, characterised by the presence of interface, as two distinct entities, whereas the ‘coalesced’ precipitate is counted as one.

The ability of the model to distinguish the particles in-contact from the coalesced particles is illustrated in Fig. 4a. This illustration highlights the detection performed by the current approach in Pb–Sn system with $80\%$ Sn-rich solid captured at 36,600 s. The corresponding micrograph is included in the bottom right quadrant of Fig. 4a. Certain sections of the micrograph with particles sharing a common interface, id est potentiallycoalescing, and coalesced precipitates are separately identified. By including the different possible detections that could be made by the model in the selected spots, its performance in accurately distinguishing the coalesced precipitates from the coalescing ones is shown in Fig. 4a. In other words, when the particles are in contact with one another, two distinct detections are possible. One, the particles can be categorised as coalesced and the other, coalescing. While in the coalesced particles, the interface is largely absent, the separating boundary is noticeable in the coalescing entities. As shown in Fig. 4a, the present model depending on the status of the interface is able accurately distinguish the coalesced precipitates from the entities sharing the common interface. On the left section of the illustration, the ability of the model to accurately detect a coalesced precipitate over the alternate possibility is shown, whereas the realisation of coalescing entities is highlighted in the top right quadrant. Owing to the abnormal morphology of the coalesced precipitate, the bounding box at times fails to completely encapsulate the fused particle. However, since the principal focus of the present detection is to ascertain the number density by accurately counting the precipitates, this deviation can reasonably be overlooked (Table 1).

The ability of the model to distinguish the coalescing precipitates from the coalesced ones, as shown in Fig. 4a, refines the accuracy of the number density estimated by the present object detection algorithm. However, the number density rendered by this approach pertains to unit area ($N_A$). Taking cognisance of the spherical shape, the relation $N_v=N_A/2<R>$, where $<R>$ is the average radii of the particles at any given instant, is adopted to ascertain the number of precipitates per unit volume.

The precipitates are segmented out of the matrix background, as shown in Fig. 4b, in order to determine the average radius. This segmentation is rendered by edge detection algorithm which subsequently facilitates the estimation of the area equivalent radius of each precipitate [24]. Combining the area equivalent radius of each precipitate and the number density per unit area, the average radius is estimated. The desired number density, $N_v$, is calculated from this average radius. The range of average radius assumed by the precipitates of different Pb–Sn systems during steady-state coarsening, ascertained in the present work, is listed in Table 1. These ranges largely agree with the existing reports [23, 24, 38].

Table 1 Estimated average radius of the precipitates (range) during coarsening

3.3 Temporal change in number density

Fig. 5

Increase in the inverse number density of precipitates with time in various Pb–Sn systems of characteristic solid fraction during steady state coarsening. Along with the regression line, confidence and prediction intervals estimated from the datapoints are superimposed on the plots of each system. Since datapoints from two different NASA missions are included, appropriate colour scheme is used to distinguish them (CSLM 1—blue and CSLM 3—red)

Microstructures of the coarsening solid–liquid mixtures of Pb–Sn systems are captured at specific stages during the evolution. In the PSI-NASA achieve [22], these micrographs are elegantly presented by distinguishing them based on volume fraction and holding time that dictates the degree of coarsening. Even though the time ranges from a minimal of 150 s to 172,800 s (48 h), for the current investigation, specific section of this period is identically considered across all volume fractions. This specific duration is chosen to indicate the steady-state coarsening, and to avoid any biases caused by the thermal gradient introduced at the later stages of the prolonged holding time. Moreover, identical duration are preferred across the different the Pb–Sn systems to facilitate comparative analysis. Stated otherwise, the micrographs reflecting the initial events are overlooked, owing to the absence of steady-state coarsening, whereas to circumvent the effect of thermal gradient, the final stages of the coarsening are left unattended. The duration pertaining to steady-state coarsening are realised by the proportional change in the number density of precipitates with time. Correspondingly, holding time between 9500 s and 86,400 s is primarily considered for the subsequent investigations, irrespective of the amount Sn-rich precipitate present in the system which includes 05$\%$, 10$\%$, 20$\%$, 30$\%$, 50$\%$, 70$\%$ and 80$\%$. Restricting the study of the microstructural changes to a specific time period, particularly in the curvature-driven evolutions, is a rather common and continuing practise  [24, 25].

3.3.1 Kinetics coefficients

For all the Pb–Sn systems with varying phase-fractions, the micrographs pertaining to the steady-state events are distinguished from the parent database which encompasses microstructures reflecting the changes all-through the holding period. The number of precipitates in these steady-state micrographs are ascertained by employing the present regression based computer-vision technique. The population of the precipitate is subsequently translated to number density per unit volume, $N_v$. The change in the number density of the precipitate is tracked during the perceived steady-state duration, between 9500 s and 86,400 s, for all the Pb–Sn mixtures with different proportions of solid Sn-rich particles. In Fig. 5, the progressive change in the number density of Sn-rich precipitates, across the various systems, are graphically presented as $1/N_v(t)$ vs t plots.

Coarsening experiments under microgravity, in similar Pb–Sn solid–liquid mixtures, have been performed as a part of more than one NASA mission. The considerable degree of overlap in the setup and the outcomes of these different experiments, which has been affirmed in earlier reports [24, 25], lends itself to a collective representation in Fig. 5. Despite an unified depiction, a distinction is made in the datapoints based on their corresponding experiments through appropriate colour scheme.

Fig. 6

The deviation of the datapoints from the linearity is estimated as RMSE and plotted. The minimal RMSE is separated from the higher value using appropriate colour scheme

It is evident from Fig. 5 that the inverse of precipitate number-density ($1/N_v$) proportionately changes with time (t) in all Pb–Sn systems of varying solid–liquid phase fractions. In order to glean the relation between the time and number density definitively, regression technique is adopted. The trend extracted by the regression treatment, for individual Pb–Sn system, is overlaid as discontinuous black lines in Fig. 5. Besides explicating the linear change in number density with time, in all systems irrespective phase fraction, the regression treatment facilitates in quantifying the kinetic coefficient. Stated otherwise, by realising a linear fit through the regression technique, the kinetic coefficient ($k_N$) dictating the coarsening rate is ascertained from its slope.

Deviation of the datapoints from the regression line is quantified in individual Pb–Sn system as root mean square error (RMSE). This RMS error of the current fit across the different systems is graphically presented in Fig. 6. RMSE for almost all Pb–Sn mixtures are largely insignificant, except for system with $5\%$ Sn-rich precipitate which exhibits relatively greater degree of deviation. The noticeable deviation of the datapoints from the linear fit, in $5\%$ solid system, can be attributed to the absence of steady-state coarsening. In other words, the linearity between the number density and time is generally indicative of steady-state coarsening. Therefore, non-compliance of the datapoints to the expected trend can be attributed to the transient coarsening that precedes the onset of steady-state evolution. This inadequate linearity in the datapoints of $5\%$ precipitate Pb–Sn system is consistent with the existing work [21].

Figure 6 that quantifies the disparity between the datapoints and regression line further indicates the significant deviation is restricted exclusively to the system with least fraction of precipitate. On the other hand, a robust linearity between the inverse number-density and time is evident in Pb–Sn mixtures with $10\%$ or greater amount of precipitate. Put differently, while Fig. 6 affirms the steady-state coarsening in all systems, its absence is noticeable in $5\%$ precipitate mixture alone. Consequently, in the subsequent investigations delineating the effect of phase fraction on steady-state coarsening Pb–Sn system with $5\%$ Sn-rich solid is reasonably excluded.

3.3.2 Confidence and prediction intervals

In Fig. 5, besides the regression line, confidence and prediction intervals are superimposed on all inverse number density plots to generate utmost statistical inferences of the exiting dataset. The data studied in the present work, for a given Pb–Sn system with characteristic phase fraction, emerges from two experiments. Even though these experiments are meticulously planned to render high-fidelity information, the number of datapoints, particularly reflecting the steady-state coarsening, are rather limited. Therefore, arguing that the increase in the number of experiments would populate the number density plot with additional datapoints that are normally distributed encompassing the existing ones, the confidence and prediction intervals are estimated. In the estimation of these intervals, the experimentally observed high-fidelity datapoints dictate the normal distribution features (mean and deviation) of the statistically assumed data. The confidence interval, in the number density plot, denotes the distribution of the mean of the statistically augmented data, whereas the distribution of the points themselves are represented by prediction interval. In Fig. 5, the intervals are developed by considering $95\%$ of the statistically-plausible datapoints. Owing to its description, the confidence interval does not always encompass the original data and corresponding regression line in Fig. 5. On the other hand, the experimental data and fitted line are invariably encapsulated by the prediction interval. The diverging trend in the confidence and prediction intervals is reflect the population and location of the datapoints. The introduction of the confidence and prediction intervals substantiate the order of the regression-line slope that reflects to coarsening kinetics.

Fig. 7

Kinetic coefficient dictating the steady-state coarsening rate of Pb–Sn system with solid content ranging from $10\%$ to $80\%$

3.4 Effect of volume fraction

The kinetic coefficient of the Pb–Sn system determining the steady-state coarsening rate is estimated from linear regression line in Fig. 6 and plotted across the corresponding volume fraction in Fig. 7. Even though there exists a visible increase in kinetic coefficient between 10 and 20% precipitate Pb–Sn system, beyond the latter $k_N$ assumes a seemingly constant value which is rather closer to the former. In other words, besides $20\%$ solid fraction system, the kinetic coefficients are apparently unaffected by the volume fraction of solids in Pb–Sn system. The rather higher value of $k_N$ in mixture with $20\%$ precipitate can reasonably be attributed to the nature of the data. Ultimately, Fig. 7 unravels that the volume fraction of particles in Pb–Sn system do not impose any significant influence of the coarsening of the respective solid–liquid mixture.

A noticeable effect of phase fraction on coarsening rate is generally expected when the evolution is governed by diffusion in the matrix. Stated otherwise, an increase in volume fraction is accompanied by an increase in the kinetic coefficient, owing to the decrease in the matrix volume separating the precipitate. The lack of any noticeable influence of precipitate fraction in Pb–Sn system, as shown in Fig. 7, points to the dominance of other mechanism, apart from matrix diffusion. The almost identical kinetics exhibited by the systems of varying volume fractions can possibly be explained by the mechanism characterising trans-interface-diffusion-controlled (TIDC) coarsening [26]. In TIDC coarsening, as opposed conventional coarsening, the diffusion rate across the interface separating the matrix and precipitate is significantly lower when compared to the solute transfer in matrix. Consequently, the mass transfer across the precipitate-matrix interface principally dictates the kinetics of TIDC coarsening. Having primarily governed by the diffusion across the interface, the effect of volume fraction in TIDC coarsening are rather minimal [39]. Accordingly, Fig. 7 seemingly indicates that the evolution in Pb–Sn systems reflects TIDC coarsening as opposed to matrix-diffusion governed evolution.

3.5 TIDC coarsening of Sn-rich precipitates

3.5.1 Number density based kinetics

Fig. 8

Relation between $N_v t^{3/n}$ and $t^{-1/n}$, along with $N_v t^{4/n}$ and $t^{1/n}$, for all Pb–Sn systems with varying phase fractions after the perceived onset of steady-state coarsening

The realisation of the trans-interface-diffusion-controlled (TIDC) coarsening behaviour exhibited by Sn-rich particles in Pb–Sn solid–liquid mixture lends itself to a more thorough analysis of kinetics based on the change in the number of precipitates, $N_v$ [40]. When the coarsening is governed by trans-interface-diffusion, the number density of precipitate can be related to the time by

$$\begin{aligned} N_v = \frac{f_e}{\eta \mathcal {S}\,(kt)^{3/n}}\left[ 1-\frac{(\tilde{\kappa } t)^{-1/n}}{f_e\Delta X_e}\right] , \end{aligned}$$

(6)

where $f_e$ indicates the equilibrium volume fraction of the precipitate, and the difference the equilibrium concentration of the solute in precipitate and matrix is denoted by $\Delta X_e$. Moreover, in Eq. (6), k is the kinetic coefficient associated with change in the average radius of the precipitate, as indicated in Eq. (1), whereas $\tilde{\kappa }$ indicates the factor dictating the progressive deviation of the solute content from the equilibrium concentration. In the estimation of the number density, the morphology of the precipitate is introduced by the shape factor, $\mathcal {S}$, which assumes a definite value. Distribution of particle size dictates parameter $\eta$ in Eq. (6).

For a relatively straightforward analysis of the change in the number density, $N_v$, the seemingly convoluted relation in Eq. (6) can be approached through [41]

$$\begin{aligned} N_v = \frac{\Phi }{t^{3/n}} - \frac{\Psi }{t^{4/n}}, \qquad \text {where} \quad \Phi =\frac{f_e}{\mathcal {S}\eta k^{3/n}} \quad \text {and} \quad \Psi =\frac{-\tilde{\kappa }^{-1/4}}{\mathcal {S}\eta k^{3/n}\Delta X_e}. \end{aligned}$$

(7)

The above re-arranged expression renders two distinct linear relations. One between $N_v t^{3/n}$ and $t^{-1/n}$ with slope and intercept equivalent to $-\Psi$ and $\Phi$, respectively. And the other, $N_v t^{4/n}$ vs $t^{1/n}$, wherein the slope is $\Phi$, and the intercept, $-\Psi$. Both set of aforementioned parameters are estimated, and their relations are graphically represented in Fig. 8, for the different Pb–Sn systems analysed in the present study. The timesteps which have already been shown to indicate the onset of steady-state coarsening (Fig. 5) is adopted for the plot in Fig. 8. This illustration, particularly the linear relation between the parameters, affirm the TIDC mechanism of coarsening in Pb–Sn systems. Even though the kinetic exponent (n) exhibits non-physical variations across the different volume fractions of the same Pb–Sn system, its values lie within the expected limit of $2\le n \ge 3$. For subsequent calculations, the exponent is reasonably treated as $n\sim 2.5$, in view of the existing report [25]. The observed differences in the exponent, n, could be attributed to the limited size of the dataset. Mean average percentage error, which considers the ratio of the deviation of the prediction and ground truth, is adopted to ascertain the best linear fit. In Appendix 1, the change in the number density of the precipitate during the entire coarsening is illustrated using $N_v t^{3/n}$ and $t^{-1/n}$, along with $N_v t^{4/n}$ and $t^{1/n}$, with succinct discussion.

Fig. 9

The interchanging slope and intercept parameters, $\Psi$ and $\Phi$, are estimated for the $N_v t^{3/n}$ vs $t^{-1/n}$ and $N_v t^{4/n}$ vs $t^{1/n}$ plots and compared across the Pb–Sn systems of different precipitate volume fractions

In addition to offering a relatively straightforward approach for affirming the mechanism of coarsening, considering $N_v t^{3/n}$ vs $t^{-1/n}$ besides $N_v t^{4/n}$ vs $t^{1/n}$, as shown in Fig. 8, facilitates in comprehending the accuracy of the undergirding investigation. As indicated earlier, the slope and intercept of the linear fit depicting the characteristic trend in $N_v t^{3/n}$ vs $t^{-1/n}$ plots gets reversed while considering the $N_v t^{4/n}$ vs $t^{1/n}$. Therefore, for a given Pb–Sn system with specific volume fraction, the parameters associated with the slope and intercept, $-\Psi$ and $\Phi$, can be compared across the two plots to ascertain the accuracy of the perceived linear trend. Extending the formulation of the mean average precision error, the deviations in parameters, $\Psi$ and $\Phi$, are estimated from the linear fit of the $N_v t^{3/n}$ vs $t^{-1/n}$ and $N_v t^{4/n}$ vs $t^{1/n}$ plots. The mismatch in these parameters, denoted as $\Psi$- and $\Phi$-deviation, across the various Pb–Sn systems is shown in Fig. 9. It is evident from this illustration that $\Psi$- and $\Phi$-deviation between the two plots for all systems, except for $20\%$ precipitate, is absolutely marginal, thereby essentially substantiating the linear trend observed in Fig. 8. In other words, the accuracy of the linear fits signifying the coarsening mechanism is established by the overlap in the slope and intercept parameters ascertained from the different plots. The significantly scattered datapoints of $20\%$ precipitate Pb–Sn system, as illustrated in Fig. 8, is primarily is responsible for the relatively noticeable deviation in parameters, $\Psi$ and $\Phi$, in Fig. 9.

3.5.2 Interfacial energy

Kinetics of coarsening, besides several factors, is governed by the energy density of the interface separating the phases in a system. Therefore, the approach adopted in the previous section to substantiate the governing mechanism of coarsening in Pb–Sn systems is further extended to estimate the interfacial energy of the boundary separating the Sn-rich precipitate from Pb–Sn liquid mixture. The energy of the interface in a two-phase system, of precipitate and matrix (liquid/solid), can be estimated from the coarsening kinetics through

$$\begin{aligned} \sigma = \frac{\Delta X_e G^{\prime \prime }}{2V_m\langle z \rangle }\left( \frac{k}{\tilde{\kappa }}\right) ^{1/n}, \end{aligned}$$

(8)

where $G^{\prime \prime }$ indicates the curvature (second derivative) of the molar Gibbs free-energy of the precipitate and $\langle z \rangle$ is the ratio of the critical and average radius [42]. Critical radius generally distinguishes the temporal evolution of the precipitate during coarsening. Depending on whether the radius of the particle is less or greater than the critical radius, it will correspondingly shrink or grow. For a two-dimensional consideration, as in the present case, the average and critical radius are considered to be equivalent [43]. Thus, the corresponding factor assumes the value of $\langle z \rangle =0.925$. The curvature of the molar Gibbs free-energy for the Sn-rich precipitate is estimated from the free energy curve rendered by CALPHAD database [44, 45] using the technique delineated in Refs. [46, 47] and outlined in Appendix 2. Moreover, the relation $\tilde{\kappa }^{-1/n}=-f_e \Delta X_e \frac{\Psi }{\Phi }$ is used to determine the parameter tracking deviation from the equilibrium concentration during coarsening.

Fig. 10

Interface energy of the boundary separating Sn-rich precipitate from Pb–Sn liquid matrix is estimated from the kinetics parameters estimated in the current work and is compared with the reported values of Refs. [48, 49]

In Fig. 10, the interfacial energy calculated for different Pb–Sn systems with varying phase-fraction based on coarsening kinetics is illustrated. Moreover, the interfacial energies of Sn-precipitate in Pb–Sn solid–liquid mixture which have been reported earlier are included in Fig. 10 [48, 49]. The reduced number of datapoints, which originally caused a variation in the kinetic exponent (n) (Fig. 8), introduces differences in the interfacial energies across the Pb–Sn systems, the present values largely surround the recent work [49]. Noticeable deviation is observed in system with $20\%$ precipitate, which can be attributed to the rather inherently scattered data.

4 Conclusion

Numerous attempts have been made to examine the constancy of the well-known Lifshitz–Slyozov–Wagner (LSW) theory, predicting the coarsening behaviour, in experimental setting [13, 17, 18, 53, 54]. These studies invariably begin with identifying an alloy system that satisfies the conditions presupposed in the framework of the LSW theory. The provision for reducing the effect of gravity in the space shuttle and ISS facilitated experimental investigations of coarsening in Pb–Sn systems at relatively lower temperature and reasonable duration. Though coarsening experiments in microgravity include a wide range of Pb–Sn systems, with typifying volume fraction of precipitates, preliminary studies largely focused on solid–liquid mixtures with minimal amount of particles, owing to its correspondence to the principal premise of the LSW theory [23, 24]. However, given the wealth of the available information, recent works have moved beyond this consideration and began analysing the effect of volume fraction on the kinetic coefficients dictating the rate of steady state coarsening [25, 55].

Initial report on two Pb–Sn systems with $15\%$ and $20\%$ Sn-rich solid indicates an increase in the kinetic coefficients with the increase in the volume fraction of precipitate, seemingly consistent with the matrix-diffusion governed coarsening [24]. However, a much recent study extending to four different volume fractions, ranging from 10 to 30% precipitate, contradicts the previous understanding and suggests a negligible effect of volume fraction [25]. In the midst of these conflicting views, the influence of volume fraction on steady-state coarsening rate has been investigated in the present work by analysing almost all Pb–Sn systems available in PSI-NASA achieve[22]. Despite their deviation from the framework of LSW theory, the systems with greater fraction of precipitates including $70\%$ and $80\%$ are considered to explicate the role of volume fraction.

Coarsening rate in the present work is estimated by monitoring the change in the number of precipitates with time. To that end, a computer vision technique based on object counting algorithm is developed to ascertain the number density of precipitates in a micrograph. By examining micrographs reflecting the system at different stages of coarsening, the temporal evolution of the corresponding number density is determined through sufficiently trained and validated object counting technique. Kinetic coefficients extracted from the change in the precipitate number density, when viewed across different systems, unravels that the rate of steady-state coarsening is rather independent of the volume fraction. Furthermore, the almost constant kinetic coefficient for six different Pb–Sn systems, with varying phase fractions, indicates dominance of an alternate coarsening mechanism, besides matrix diffusion. This observation, substantiated by existing report [25], indicates that precipitates in Pb–Sn system exhibit trans-interface-diffusion-controlled (TIDC) coarsening, and thereby turning this alloy ill-suited for studying the effect of volume fraction on coarsening [26, 39].

Appendices

Appendices

1.1 Appendix 1

Fig. 11

Kinetics of evolution using $N_V t^{3/n}$ vs $t^{-1/n}$ and $N_V t^{4/n}$ vs $t^{1/n}$ plots for the entire duration of coarsening in Pb–Sn system of different volume of precipitate

Illustration in Fig. 8 is extended to include entire duration of coarsening in Pb–Sn solid–liquid mixture of varying phase fractions and shown in Fig. 11. The fit realised for the time span well beyond the initial stages (Fig. 8) included in this depiction. Though a common trend could be perceived in both $N_V t^{3/n}$ vs $t^{-1/n}$ and $N_V t^{4/n}$ vs $t^{1/n}$ plots across the different systems, the linearity is largely confined to the final stages. In other words, if the linear relation between the parameters is deemed to indicate a characteristic mode of coarsening, as in matrix-diffusion governed evolution, Fig. 11 suggests the steady-state transformation is induced in trans-interface-diffusion-controlled (TIDC) coarsening at later stages after certain degree of initialisation.

1.2 Appendix 2: Extracting second derivative of free-energy

Even though ascertaining the second derivative of the Gibbs free-energy curve, particularly for binary systems, is extensively discussed in Refs. [46, 47], for the ease of readers, a general outline is offered in this section. Mounting thermodynamic databases onto suitable tools, like ThermoCalc and Pandat, Gibbs free-energy for specific compositions can be determined. Sufficient information on compositions and corresponding free-energies, in binary systems, facilitates in realising a second-degree equation for the free-energy-composition curve. In this present work, five-point stencil scheme of the finite-difference approach has been adopted to extract the numerical expression for the binary free-energy curve. By exploiting the identical chemical potential of solute across the phases in equilibrium, the accuracy of the numerically-fitted curve is verified through Newton–Raphson iteration technique. From the realised expression of the curve, the second derivation of the Gibbs free-energy, $G^{\prime \prime }$, is determined.