1 Introduction

Nonlinear materials have stimulated much interest due to their important role in the development of modern photonics and optoelectronics [1]. Thus, much effort has been devoted to understanding the nonlinear polarization mechanisms and their relation to the structural characteristics of nonlinear materials [2]. Intense light fields are indeed required to manipulate the optical properties of materials and induce nonlinear phenomena. The effective nonlinear optical response can fortunately be induced with low light intensity through interaction with plasmonic materials [3,4,5,6]. Specifically, when the light fields interact with the free electrons on the surface of metals, they induce collective oscillations called surface plasmons resulting in strong local electromagnetic fields that can enhance the nonlinearity of the plasmonic systems [7]. Moreover, nanoplasmonics enable strong light-matter interaction with a high density of states that can lead to additional efficiency of energy conversion [8, 9]. Interestingly, controlling the optical properties of the hybrid nanoplasmonic systems, where the energy can transfer between the components of the systems, [10,11,12,13,14,15,16] provides a promising platform for energy conversion devices such as photovoltaic devices [17,18,19,20,21,22].

In photovoltaic devices, maximizing absorption is desirable to create additional electron–hole pairs that initiate generation with appreciable efficiency. The nonlinear optical properties relate to higher efficiency of mobility and electron transport from donor to acceptor. Due to the ability of plasmonics to induce nonlinearity with low light intensity, some undesirable nonlinear processes that reduce the energy conversion efficiency such as two-photon absorption can be avoided [23]. It has been shown that the materials of high third-order nonlinearity with low light intensity can be employed in solar cell applications [24, 25]. Therefore, plasmonic nanocompositions, where electromagnetic fields experience a large enhancement even with low light intensity and exhibit a large third-order nonlinearity within a tunable spectral region controlled by the size and dielectric properties of these materials, can be used to build efficient devices for energy conversion [5, 26,27,28]. The enhanced nonlinear absorption of radiation in the visible and near-infrared regions with good stability is an essential parameter that can be used to measure the efficiency of solar cells.

It has been found that cross-Kerr nonlinearity describing cross-coupling effects is twice as large as that of self-action effects [29]. More precisely, the cross-Kerr nonlinearity describes the change in refractive index experienced by an electric field propagating in the Kerr medium and controlled by another applied field. Because the significant potential applications of cross-Kerr nonlinearity in optical devices [30,31,32], several schemes have been theoretically and experimentally studied to control this type of nonlinearity and suggest suitable applications. [33,34,35,36,37,38,39,40,41,42]. In most cases, the large Kerr nonlinearity with a changeable sign is often needed to gain conversion efficiency [43]. Thus, cross-Kerr nonlinearity has been examined for some plasmonic systems. H. Rhman et al. have examined cross-Kerr nonlinearity in surface plasmon waves generated at the interface between graphene and gain medium [44]. It has been shown that the propagation length of the surface plasmons can be significantly controlled under Kerr nonlinearity and strength of the control fields. Moreover, high cross nonlinear refractive index has been observed in a five-level quantum system near plasmonic nanostructure via probe field amplification [45].

Interestingly, taking advantage of high mobility and the long propagation distances of the charge carriers in the graphene, in addition to the high charge density in a metal as well as the relatively low decay rate and localized charges in quantum dots which can induce atomic coherence if they are modeled as muli-level atomic systems, graphene nanodisks-metal nanoparticles-quantum dots (GNDs-MNPs-QDs) hybrid plasmonic system has been proposed by M. Tohari et al. which demonstrates ultrafast dynamics [46] and a giant self-Kerr nonlinearity [5] in the visible region of the electromagnetic spectrum with low light intensity can be controlled in magnitude and sign by the parameters of the system enabling various interesting potential applications in photonics and optoelectronics.

Motivated by the high nonlinearity that has been recently shown in our proposed hybrid plasmonic system [5, 47, 48], we analytically investigate in the present paper the nonlinear absorption coefficient of the system experienced by the probe field due to another applied control field resulting in the cross-Kerr effect. The probe field is adjusted to be resonant with surface plasmons of visible energy that matches the gain energy of the quantum dots. The metal nanoparticle that has the ability to control the optical properties of the adjacent graphene nanodisk is also inserted in the system.

The paper is organized as follows: in “Theoretical model” the model is established by describing the relevant mathematical techniques and the physical assumptions. Section “Results and discussion” displays the numerical simulations and discusses the analytical results of cross-Kerr nonlinearity of the system and “Conclusions” summarizes the main conclusions.

2 Theoretical model

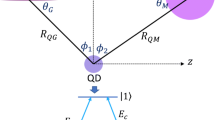
Suppose a hybrid plasmonic system depicted in Fig. 1 consisting of GND of radius \(L_{z}\) and thickness \(L_{x}\) doped at Fermi energy \(E_{F}\) with mobility of \(\mu\) for charge carriers. The GND is placed at a distance \(R_{GQ}\) from the quantum dot modeled as a three -level atomic system of \(\Lambda\) configuration. Additionally, a MNP is inserted within the system at distances \(R_{GM}\) and \(R_{QM}\) from the GND and QD respectively. The QD of a three-level atomic system of \(\Lambda\) configuration interacts with two applied fields, probe and control fields. Due to the unique properties of graphene charge carriers, the surface plasmons of GND is set to be resonant with the excitons of QD.The MNP is incorporated in the system to control the optical properties of the GND [46]. The probe field \(E_{P}\) is monitored to be resonant with surface plasmons of GND at the visible region of the electromagnetic spectrum inducing the transition \(\mathinner {|{1}\rangle }\longleftrightarrow \mathinner {|{2}\rangle }\) with dipole moment \(\mu _{12}\) and decay rate \(\gamma _{12}\). On the other hand, the transition \(\mathinner {|{1}\rangle }\longleftrightarrow \mathinner {|{3}\rangle }\) is mediated by the control field \(E_{c}\) with dipole moment \(\mu _{13}\) and decay rate \(\gamma _{13}\).

Fig. 1
figure 1

The MNP–GND–QD hybrid system setup

Full size image

Analyzing the dipole-dipole interaction between the components of the system, one can use the corresponding interaction Hamiltonian given in terms of the dipole field felt by the QD to obtain the following equation of motion for the matrix elements of the density operators that describe the dynamics of the system [46]:

$$\begin{aligned} \dot{\rho }_{13}= & {} -\left[ \left( \frac{\gamma _{13}}{2}+\frac{\gamma _{12}}{2}\right) +i\left( \Delta _{c}-\Lambda _{z}\left( \rho _{33}-\rho _{11}\right) \right) \right] \rho _{13}\nonumber \\{} & {} \quad +i\Omega _{c}\left( \Pi _{z}+\Phi _{z}\right) \left( \rho _{33}-\rho _{11}\right) +i\left[ \Omega _{p}\left( \Pi _{x}+\Phi _{x}\right) +\Lambda _{x}\rho _{12}\right] \rho _{23}, \end{aligned}$$
(1a)
$$\begin{aligned} \dot{\rho }_{12}&= -\left[ \left( \frac{\gamma _{13}}{2}+\frac{\gamma _{12}}{2}\right) +i\left( \Delta _{p}-\Lambda _{x}\left( \rho _{22}-\rho _{11}\right) \right) \right] \rho _{12}\nonumber \\{} & {} \quad +i\Omega _{p}\left( \Pi _{x}+\Phi _{x}\right) \left( \rho _{22}-\rho _{11}\right) +i\left[ \Omega _{c}\left( \Pi _{z}+\Phi _{z}\right) +\Lambda _{z}\rho _{13}\right] \rho _{32}, \end{aligned}$$
(1b)
$$\begin{aligned} \dot{\rho }_{32}= & {} -\left( \frac{\gamma _{32}}{2}+i\Delta _{2}\right) \rho _{32}+i\left[ \Omega _{c}^{*}\left( \Pi _{z}^{*}+\Phi _{z}^{*}\right) +\Lambda _{z}^{*}\rho _{31}\right] \rho _{12}\nonumber \\{} & {} \quad -i\left[ \Omega _{p}\left( \Pi _{x}+\Phi _{x}\right) +\Lambda _{x}\rho _{12}\right] \rho _{31}, \end{aligned}$$
(1c)
$$\begin{aligned} \dot{\rho }_{11}= & {} -\left( \gamma _{12}+\gamma _{13}\right) \rho _{11}+i\left[ \Omega _{c}\left( \Pi _{z}+\Phi _{z}\right) +\Lambda _{z}\rho _{13}\right] \rho _{31}\nonumber \\{} & {} \quad +i\left[ \Omega _{p}\left( \Pi _{x}+\Phi _{x}\right) +\Lambda _{x}\rho _{12}\right] \rho _{21}+c.c., \end{aligned}$$
(1d)
$$\begin{aligned} \dot{\rho }_{22}= & {} \gamma _{12}\rho _{11}+\gamma _{32}\rho _{33}-i\left[ \Omega _{p}\left( \Pi _{x}+\Phi _{x}\right) +\Lambda _{x}\rho _{12}\right] \rho _{21}+c.c., \end{aligned}$$
(1e)
$$\begin{aligned} \dot{\rho }_{33}= \,& {} \gamma _{13}\rho _{11}-\gamma _{32}\rho _{33}-i\left[ \Omega _{c}\left( \Pi _{z}+\Phi _{z}\right) +\Lambda _{z}\rho _{13}\right] \rho _{31}+c.c. \end{aligned}$$
(1f)

where \(\Pi _{x,z}\), \(\Phi _{x,z}\) and \(\Lambda _{x,z}\) are the dipole-dipole interaction factors that are given in terms of the geometrical features of the system as [46]:

$$\begin{aligned} \Pi _{x}& = {} \frac{1}{4\pi \epsilon ^{*}}\left[ \frac{\alpha _{G}^{x}\left( 3\cos \phi _{1}-1\right) }{R_{QG}^3}+\frac{\alpha _{M}\left( 3\cos \phi _{2}-1\right) }{R_{QM}^3}\right] , \end{aligned}$$
(2a)
$$\begin{aligned} \Lambda _{x} &= \frac{\mu _{12}^{2}}{\left( 4\pi \epsilon ^{*}\right) ^{2}\hbar \epsilon _{0}\epsilon _{b}}\left[ \frac{\alpha _{G}^{x}\left( 3\cos \phi _{1}-1\right) ^2}{R_{QG}^6}+\frac{\alpha _{M}\left( 3\cos \phi _{2}-1\right) ^2}{R_{QM}^6}\right] , \end{aligned}$$
(2b)
$$\begin{aligned} \Phi _{x}&= \frac{-\alpha _{G}^{x}\alpha _{M}}{\left( 4\pi \epsilon ^{*}\right) ^{2} R_{GM}^3 }\left[ \frac{3\cos \phi _{1}-1}{R_{QG}^3}+\frac{3\cos \phi _{2}-1}{R_{QM}^3}\right] , \end{aligned}$$
(2c)
$$\begin{aligned} \Pi _{z}&= \frac{1}{4\pi \epsilon ^{*}}\left[ \frac{\alpha _{G}^{z}\left( 3 \cos \theta _{G} -1\right) }{R_{QG}^3}+\frac{\alpha _{M}\left( 3 \cos \theta _{M} -1\right) }{R_{QM}^3}\right] , \end{aligned}$$
(2d)
$$\begin{aligned} \Lambda _{z}&= \frac{\mu _{13}^{2}}{\left( 4\pi \epsilon ^{*}\right) ^{2}\hbar \epsilon _{0}\epsilon _{b}}\left[ \frac{\alpha _{G}^{z}\left( 3\cos \theta _{G}-1\right) ^2}{R_{QG}^6}+\frac{\alpha _{M}\left( 3\cos \theta _{M}-1\right) ^2}{R_{QM}^6}\right] , \end{aligned}$$
(2e)
$$\begin{aligned} \Phi _{z}&= \frac{2\alpha _{G}^{z}\alpha _{M}}{\left( 4\pi \epsilon ^{*}\right) ^{2} R_{GM}^3 }\left[ \frac{3\cos \theta _{G}-1}{R_{QG}^3}+\frac{3\cos \theta _{M}-1}{R_{QM}^3}\right] . \end{aligned}$$
(2f)

\(\alpha _{G}^{x}\) (\(\alpha _{G}^{z}\)) is the shape-dependent polarizability of GND induced by x-polarized (z-polarized) light given in terms of the dimensions of GND, depolarization factors resulting from the asymmetry of GND [46], the dielectric constants of GND and the surrounding medium. \(\epsilon ^{*} = (2\epsilon _{b}-\epsilon _{q})/ 3\epsilon _{b}\) is the effective dielectric constant, where \(\epsilon _{b}\) and \(\epsilon _{q}\) are the dielectric constants of background and the QD respectively. Similarly, \(\alpha _{M}\) is the shape-dependent polarizability of MNP given in terms of its dimensions and the dielectric constants of MNP and the surrounding medium. Remarkably, the angles and distances between the components of the system are governed by the triangle law.

$$\begin{aligned} \chi&=\frac{2iNd_{12}}{\epsilon _{0} E_{p}}\frac{\Omega _{p}\left( \Pi _{x}+\Phi _{x}\right) }{F}\nonumber \\&\times \left[ \left( 1-\frac{2\gamma _{32}}{2\gamma +\gamma _{12}}\right) -\frac{4\Omega _{p}^{2}|\Pi _{x}+\Phi _{x}|^{2}}{2\gamma +\gamma _{12}}\left( \frac{1}{F}+\frac{1}{F^{*}}+\frac{i(\Lambda _{x}-\Lambda _{x}^{*})}{|F |^{2}}\right) \right] \end{aligned}$$
(3)

Using an iterative technique, where the density matrix element can be written as \(\rho _{nm}=\rho _{nm}^{(0)}+\rho _{nm}^{(1)}+\rho _{nm}^{(2)}+\cdots\), and at steady state under the weak probe field approximation where the control field is much stronger than the probe field, i.e. \(\rho _{11}^{(0)}=0\) and \(\rho _{22}^{(0)}=1\), M. Tohari et al. have found that the total susceptibility of the system can be given as [5]: To study the nonlinearity of the system resulting from the cross-Kerr effect due to the applied control field, we need to write the total susceptibility of the system in terms of control field i.e., \(\chi =\chi ^{(1)}+3\chi ^{(3)}E_{c}^{2}\). This requires to make the Taylor expansion over \(\Omega _{c}\) to eventually obtain:

$$\begin{aligned} \chi ^{(1)}= & {} A\times \left[ \frac{1}{B}\left( 1-\frac{2\gamma _{32}}{2\gamma +\gamma _{12}}\right) -4\Omega _{p}^{2}\frac{\Pi _{x}+\Phi _{x}}{2\gamma +\gamma _{12}}\left( \frac{1}{B^{2}}+\frac{1}{B^{2}}+i\frac{\Lambda _{x}-\Lambda _{x}^{*}}{B^{2}+B^{*}} \right) \right] \end{aligned}$$
(4)
$$\begin{aligned} \chi ^{(3)}= & {} A\left( \frac{C}{B^{2}}\right) \left( 1-\frac{2\gamma _{32}}{2\gamma +\gamma _{12}}\right) \nonumber \\{} & {} \quad -A\left( \frac{4|\Pi _{x}+\Phi _{x}|^{2}}{2\gamma +\gamma _{12}} \right) \left[ \frac{2C}{B^{3}}+\frac{C}{B^{*}B^{2}}+\frac{C^{*}}{{B^{*}}^{2}B}+(\Lambda _{x}-\Lambda _{x}^{*})\left( \frac{2C}{B^{*}B^{3}}+\frac{C^{*}}{{B^{*}}^{2}B^{*}}\right) \right] \end{aligned}$$
(5)

where

$$\begin{aligned} A&= \frac{-4iN\mu _{12}\mu _{13}^{2}}{3\epsilon _{0}\hbar ^{2}E_{p}}(\Pi _{x}+\Phi _{x})\Omega _{p} \end{aligned}$$
(6)
$$\begin{aligned} B&= \left( \frac{\gamma _{12}}{2}+\frac{\gamma _{13}}{2}\right) +i(\Delta _{p}-\Lambda _{x}) \end{aligned}$$
(7)
$$\begin{aligned} C&= \frac{|\Pi _{z}+\Phi _{z}|^{2}}{\gamma _{32}/2+i\Delta _{2}} \end{aligned}$$
(8)

In terms of third-order nonlinear susceptibility that describes the cross-Kerr effect, cross Kerr nonlinear refractive index \(n_{2}\) and the corresponding nonlinear absorption coefficient \(\beta\) are [29]:

$$\begin{aligned} n_{2}&= \frac{3Re\left[ \chi ^{(3)}\right] }{2\epsilon _{0} c n_{0}^{2}} \quad \text {and} \quad n_{0}=\sqrt{1+Re\left[ \chi ^{(1)}\right] } \end{aligned}$$
(9a)
$$\begin{aligned} \beta&= \frac{\omega }{\epsilon _{0} c^{2} n_{0}^{2}} Im\left[ \chi ^{(3)}\right] \end{aligned}$$
(9b)

3 Results and discussion

In this section we illustrate the analytical results for the nonlinear absorption coefficient for the hybrid plasmonic system depicted in Fig. 1. Specifically, for a monolayer GND of thickness \(L_{x}={0.35}\,\hbox {nm}\) and radius \(L_{z}={7}\,\hbox {nm}\) [49], doped at level \(E_{F}={1.36}\,\hbox {e V}\) and has charge carriers of mobility \(\mu =10^{4}\,\hbox {cm}^{2}\hbox {V}^{-1} \hbox {s}^{-1}\) embedded in a GaAs background. For these parameters, two plasmonic resonances can be induced by x and z polarized light fields, \(\hbar \omega _{sp}^{x}={2.1724}\, {\hbox {e V}}\) and \(\hbar \omega _{sp}^{z}={0.6418}\, {\hbox {e V}}\) [5]. Since we aim to study the efficiency of the present system as a photovoltaic device, we choose the visible resonance \(\hbar \omega _{sp}^{x}= {2.1724}\, {\hbox {e V} }\) which matches the exciton energy of CdSe QD of atomic density \(N=10^{20}\hbox {m}^{-3}\) modelled as a three-level atomic system of \(\Lambda\) configuration as illustrated in Fig. 1  [5]. The parameters of the QD are set to be \(\mu _{12}=\mu _{13}={1}{\hbox {enm}}\), \(\gamma _{12}=\gamma _{13}={1}\,\hbox {GH}_{\hbox {z}}\) and \(\gamma _{32}=0.35 \gamma _{12}\). Due to being a noble metal and its efficiency as a plasmonic material resulting from the high plasma frequency, a spherical silver nanoparticle of a high-frequency dielectric constant of \(\epsilon _{\infty }^{M}=5\), plasmon energy of \({9}\,\hbox {e V}\) and plasmon damping of \(\gamma _{M}={100}\,\hbox {TH}_{\hbox {z}}\) is inserted in the system [50]. Note that, we apply a control field with a relatively low intensity corresponding to \({1}\,\hbox {MH}_{\hbox {z}}\) i.e. \({58}\,\hbox {mW}/\hbox {m}^{2}\). To practically facilitate the setup, the inclination angles of the two plasmonic components with respect to the QD \((\theta _{M}, \theta _{G})\) are chosen to be equal and relatively large i.e. \(\theta _{M}= \theta _{G}={1}\,\hbox {rad}\).

Fig. 2
figure 2

Cross-Kerr nonlinearity versus probe field detuning of the MNP-GND-QD hybrid system of geometry \(\theta _{M}=\theta _{G}={1}\,\hbox {rad}\), \(R_{M}={15}\,\hbox {nm}\), for different values of R. The system interacts with the resonant control field of \(\Omega _{c}={1}\,\hbox {MH}_{\hbox {z}}\) and the probe field of \(\Omega _{p}=0.01\Omega _{c}\)

Full size image

In the following, we study the nonlinear absorption coefficients of the GND-MNP-QD hybrid system experienced by the probe field due to applying the control field. The effect of the edge-to-edge distances between GND and MNP (R) is examined in Fig. 2. Although we use low light intensity, the system exhibits giant cross-Kerr nonlinearity, compared to other nonlinear systems, can be controlled in magnitude and sign by the parameters of the system [45, 51]. In particular, the plasmonic system demonstrates large absorption coefficients that can be significantly controlled by the distances between the two plasmonic components. As the two plasmonic components come close to each other, the proposed plasmonic system exhibits large nonlinear absorption coefficients at exact resonance due to the corresponding strong dipole-dipole interaction between the components of the system. Obviously, the sign of the nonlinear absorption coefficient can be controlled by the probe field detuning. Moreover, it can be seen that the negative proportion of nonlinear absorption coefficient increases for small distances between the two plasmonic components implying the efficiency of the MNP-GND-QD hybrid system in nonlinear applications that require a switching between amplification and absorption. In fact, it is well-known that the coupling of plasmons is highly distance-dependent which stimulates many studies to suggest experimental techniques to control these distances such as nanolithography and related techniques [52, 53] that are limited in creating very small and well-defined inter-nanoparticle distances of few nanometers. Moreover, polymers and biomolecules can be used as spacers to tune the inter-nanoparticle distances of colloidal nanoparticles [54]. Therefore, the possibility to control the distances between plasmonic particles of the system provides an interesting property to control plasmonic photovoltaic devices.

Fig. 3
figure 3

Nonlinear absorption coefficient versus probe field detuning of the MNP-GND-QD hybrid system of geometry \(\theta _{M}=\theta _{G}={1}\,\hbox {rad}\), \(R={30}\,\hbox {nm}\), for different values of \(R_{M}\). The system interacts with the resonant control field of \(\Omega _{c}={1}\hbox {MH}_{\hbox {z}}\) and the probe field of \(\Omega _{p}=0.01\Omega _{c}\)

Full size image

Recently, it has been shown that the presence of MNP within the hybrid system can significantly improve the energy transfer between GND and QD [46]. Thus, the effect of the MNP size on nonlinear absorption coefficients is explored in Fig. 3. We observe that the nonlinear absorption coefficient is sensitive to the size of MNP. In particular, for relatively large size of the MNP, the nonlinear absorption of the system is significantly enhanced. Additionally, the sign of the nonlinear absorption coefficient can be controlled by the detuning of the probe field in addition to the size of the MNP providing a promising platform for many optical devices. To get a complete picture of the impact of both the edge-to-edge distances between the MNP and the GND (R) as well as the radius of the MNP \((R_{M})\), we study in Fig. 4 the behavior of the relation between the nonlinear absorption coefficient and the ratio \(R/R_{M}\). Remarkably, the maximum values of the nonlinear absorption coefficients are obtained for a small \(R/R_{M}\), when the separation between the MNP and GND is double the radius of the MNP. As the ratio \(R/R_{M}\) increases the nonlinear absorption coefficient significantly decreases. For \(R/R_{M}>3.5\), the nonlinear absorption coefficient vanishes as illustrated in Fig. 4.

Fig. 4
figure 4

Nonlinear absorption coefficient versus the ratio \(R/R_{M}\) of the MNP-GND-QD hybrid system of geometry \(\theta _{M}=\theta _{G}={1}\,\hbox {rad}\). The system interacts with the resonant control field of \(\Omega _{c}={1}\,\hbox {MH}_{\hbox {z}}\) and the probe field of \(\Omega _{p}=0.01\Omega _{c}\)

Full size image

Furthermore, due to the important role of the control field in the nonlinearity of the system via inducing the cross-Kerr effect, we examine the impact of the detuning of the control field on the nonlinear absorption coefficients in Fig. 5. Obviously, for resonant control field, we obtain a relatively large value of nonlinear absorption. As the ratio \(\Delta _{c}/ \gamma _{12}\) increases, the nonlinear absorption coefficients are significantly reduced and the peaks of the nonlinear absorption spectra are displaced to larger values along a wider band of the probe field detuning. Remarkably, the sign of the nonlinear absorption coefficients can be monitored by the detuning of the control field in addition to the detuning of the probe field.

Fig. 5
figure 5

Nonlinear absorption coefficient versus probe field detuning of the MNP-GND-QD hybrid system of geometry \(\theta _{M}=\theta _{G}={1}\,\hbox {rad}\), \(R={30}\,\hbox {nm}\) and \(R_{M}={15}\,\hbox {nm}\), for different values of \(\Delta _{c}\). The system interacts with the resonant control field of \(\Omega _{c}={1}\,\hbox {MH}_{\hbox {z}}\) and the probe field of \(\Omega _{p}=0.01\Omega _{c}\)

Full size image

Since the stability of the nonlinear system is a fundamental requirement for its significance in real-world applications, we check in Fig. 6 the behavior of the nonlinear absorption coefficients under the influence of a small variation of the geometrical parameters, i.e. the edge-to-edge distances between the GND and the MNP as well as the strength of the control field. Obviously, the nonlinear absorption of the system experiences a slight change as a result of small variations of its geometrical parameters despite the strong nonlinearity demonstrated by the system. Moreover, the system exhibits a good stability against considerable changes in the strength of the control field. When the control field becomes strong enough to induce electromagnetically induced transparency (EIT) i.e. 1.7 PHz, the nonlinear absorption coefficient is reduced associated with EIT window at exact resonance as shown in Fig. 6.

Fig. 6
figure 6

Nonlinear absorption coefficient versus probe field detuning of the MNP-GND-QD hybrid system of geometry \(\theta _{M}=\theta _{G}={1}\,\hbox {rad}\), \(R_{M}={15}\,\hbox {nm}\) and \(R={30}\,\hbox {nm}\) (b). The system interacts with the control field of \(\Omega _{c}={1}\,\hbox {MH}_{\hbox {z}}\) (a) and the probe field of \(\Omega _{p}=0.01\Omega _{c}\)

Full size image

To conclude, from the above results, it is clear that the MNP-GND-QD hybrid system exhibits giant cross-Kerr nonlinearity compared to other plasmonic systems [44, 45]. Remarkably, the presence of the QD near the two plasmonic components, GND and MNP, can significantly enhance its cross-Kerr nonlinearity. This result can be attributed to the electric field enhancement in the MNP-GND-QD hybrid system recognized from the equation of motion for the density matrix elements Eq. 1, where the Rabi frequency of the electric field is enhanced by the factor \((\Pi _{x,z}+\Phi _{x,z})\) resulting from the dipole-dipole interaction between the components of the system. The obtained controllable large nonlinear absorption coefficients in the visible region of the electromagnetic spectrum associated with good stability emphasizes the importance of the system for constructing efficient photovoltaic devices with limited losses and high efficiency due to the low light intensity required to demonstrates this giant cross-Kerr nonlinearity.

4 Conclusion

We have studied the cross-Kerr of the MNP-GND-QD hybrid system experienced by the probe field due to the presence of another control field. We have derived an analytical expression for the third-order nonlinear susceptibility of cross-Kerr nonlinearity. A giant cross-Kerr nonlinearity is obtained that can be controlled by the geometrical features of the system in addition to the detuning of both probe and control fields. Interestingly, the system exhibits large nonlinear absorption coefficients in the visible region of the electromagnetic spectrum with low light intensity for small distances between the MNP and the GND and large size of the MNP as well as the small detuning of the control field. Specifically, large values of cross-Kerr nonlinear absorption coefficient are obtained for a resonant control field with a ratio of the separation between GND and MNP to the size of MNP is equal to 2. Moreover, a controllable switching between positive and negative nonlinear absorption is observed that implies the possibility of using the MNP-GND-QD hybrid system in various applications that require amplification and absorption.

The large nonlinear absorption coefficients with good stability in the visible region of the electromagnetic spectrum demonstrated by our proposed plasmonic system emphasizes that the system can provide a promising platform for photovoltaic devices. We hope that our study will stimulate more efforts to experimentally examine the nonlinear properties of our proposed MNP-GND-QD hybrid system and its potential applications.