1 Introduction

First introduced by Schmid in 1994 [1], a multiferroic material possesses two or three ferroic properties; ferromagnetism, ferroelectricity, and ferroelasticity simultaneously in the same phase. However, a fourth ferroic type exists, ferrotoroidicity whereby toroidal moments order spontaneously [2]. A ferrotoroidic material can break both time-reversal and space-inversion symmetries simultaneously without necessarily developing ferromagnetism or ferroelectricity [3, 4]. The coupling between these ferroic properties opens possibilities for a wide range of new applications in electronic devices and sensors [5,6,7]. These materials are the most promising for multiple-state memory devices where data are stored electrically and read magnetically with small power consumption and for the spin valves that are tunable with an electric field [8,9,10]. Manganite RMnO3 (an important class of multiferroic materials) has been a fascinating research subject for decades [11,12,13,14,15,16,17,18,19,20], due to their interesting physical properties, especially the ones with Mn3+ cations because of interplay between orbital and spin degrees of freedom [21]. The rare earth manganite perovskite RMnO3 can be structurally divided into two subsystems. One with the larger rare earths, R = La–Dy, where an orthorhombically distorted perovskite structure Pbnm is adopted (o-RMnO3), while for the smaller rare earths, R = Sc, Y and Ho–Lu, the structure is hexagonal P63cm (h-RMnO3) [22, 23]. Also, manganite RMnO3 can have different spin ordering structures depending on Mn–O–Mn bond angles [24, 25]. RMnO3, where R = La–Gd, has A-type antiferromagnetic (AFM) structures with small spin canting arising in weak ferromagnetic (FM) properties and without spin-induced ferroelectricity [21]. For RMnO3 where R = Tb and Dy, they have cycloidal spin structures, with spin-induced ferroelectric properties [26, 27]. E-type AFM structures are formed in RMnO3 with R = Ho–Lu and Y, where these structures also produce large spin-induced ferroelectric polarization from the exchange striction mechanism [28, 29]. YMnO3 can adopt both hexagonal and orthorhombic structures [30, 31], but the later phase can be obtained only under high pressure [32, 33] or by special synthesis methods, for instance, soft chemical method or mechano-chemical synthesis [34,35,36], low-temperature soft chemistry [25, 37, 38] or epitaxial thin-film growth [39, 40].

The orthorhombic perovskite YMnO3 exhibits an antiferromagnetic transition at TN ~ 40 K while the ferroelectric transition takes place at about 30 K [28, 41]. The hexagonal YMnO3 undergoes a transformation from a paramagnetic (PM) to an A-type antiferromagnetic (AFM) ordered state, TN ~ 70 K [42]. The transition from the high-temperature paraelectric phase of the P63/mmc YMnO3 to the low-temperature ferroelectric phase of the P63cm crystal occurs at 1270 K [43, 44] resulting in a tripling of the unit cell and at 913 K a ferroelectric anomaly leading to asymmetric displacement of the Y3+ ions [45]. The Mn3+ ions are in a high-spin state S = 2 [46]. The hexagonal structure consists of non-connected layers of vertex-sharing trigonal MnO5 bipyramids corner-linked by in-plane oxygen ions (OP) with apical oxygen ions (OT) establishing closely packed planes separated by layers of eightfold coordinated Y3+ ions [47]. Ferroelectricity in YMnO3 is suggested to emerge from the MnO5 polyhedra distortion, joined by the triangular and layered network and the unusual Y3+ coordination [43].

However, the manganites have one very serious drawback. With few exceptions, optimally doped lanthanum–strontium and lanthanum–barium manganites, the majority of manganites, including those studied in this paper, have magnetic and electrical transition temperatures significantly lower than the room temperature [21]. This fact seriously limits the practical significance of these materials. Despite their fundamental importance, as model objects of study, this remains very high. Since the Ferrites are another class of compounds, they are important for practical use [48, 49]. Furthermore, large spontaneous polarization and multiferroic properties at room temperature are recently discovered in barium hexaferrites substituted by diamagnetic cations. Herewith, the magnetoelectric characteristics of M-type hexaferrites, fabricated by a modified ceramic technique, are more advanced than those for the well-known room-temperature BiFeO3 orthoferrite multiferroic [50, 51].

The purpose of this study is to discuss a theoretical investigation of the magnetic properties of the manganite oxide perovskite YMnO3 structures using Monte Carlo simulations [43,44,45,46,47,48,49,50,51] under the standard Metropolis algorithm. To reach this goal, a thoughtful analysis of the magnetizations and susceptibilities as a function of the temperature has been carried out. We also analyzed and discussed the effects of the crystal field, the external magnetic field, the exchange coupling interactions and temperature on the behavior of the hysteresis cycles [52,53,54,55,56,57,58,59].

This work is organized as follows: in Sect. 2, we illustrate and present the model and the theoretical formulations. Section 3 is dedicated to the discussion of the obtained Monte Carlo results. We present our conclusions in Sect. 4.

2 Model and simulation method

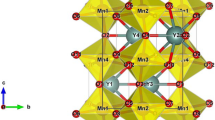
The yttrium manganite oxide YMnO3 can crystallize in either hexagonal or orthorhombic crystal structure. This happens while undergoing a transformation from hexagonal structure to an orthorhombic one under special synthesis methods and high pressure [10]. This study is devoted to the magnetic properties of the two structures of the manganite oxide perovskite YMnO3, using Monte Carlo simulations under Metropolis algorithm [60] in the framework of the Ising model [61]. The orthorhombic structure is presented in Fig. 1, with the space group Pbnm (n°62) and the lattice parameters a = 5.2580 Å, b = 5.8361 Å and c = 7.3571 Å [62]. Moreover, Fig. 2 illustrates the hexagonal structure, with the space group P63cm (n°185) and the lattice parameters a = 6.1483 Å and c = 11.3993 Å [62]. The magnetic ordering of this compound in both structures occurs under the manganese moments. The following Hamiltonian governs the two structures of the studied system:

$${\mathcal{H}} = - J_{\text{intra}} \mathop \sum \limits_{{\left\langle {i,j} \right\rangle }} S_{i} S_{j} - J_{\text{inter}} \mathop \sum \limits_{{\left\langle {i,k} \right\rangle }} S_{i} S_{k} - H\mathop \sum \limits_{i} S_{i} - \Delta \mathop \sum \limits_{i} S_{i}^{2} ,$$
(1)

where the notations \(\left\langle {i,j} \right\rangle\) and \(\left\langle {i,k} \right\rangle\) represent the summations running over the first nearest neighbor spins in the same plane, and different planes along the z-axis, respectively. The spins Si are the manganese magnetic moments of atoms taking the values of ± 1, ± 2 and 0. The exchange coupling interactions \(J_{\text{intra}}\) (in the same plane) and \(J_{\text{inter}}\) (between different planes) are the interactions between the magnetic Mn–Mn atoms. The crystal field Δ is originated from the interaction between Mn and the O atoms. In fact, the oxygen atoms are responsible for the presence of the crystal field, which appears in the expression of the Hamiltonian given in Eq. (1). The external magnetic field H is applied to the all system spins.

Fig. 1
figure 1

The (o-YMO) orthorhombic crystal structure of YMnO3, showing the magnetic element Mn using Vesta software [63]

Full size image
Fig. 2
figure 2

The (h-YMO) hexagonal crystal structure of YMnO3, showing the magnetic element Mn using Vesta software [63]

Full size image

To simulate the magnetic behavior of the studied system, we carried out Monte Carlo simulations under the Metropolis algorithm using the Hamiltonian given in Eq. (1).

The total energy of the system is given by

$$E = \frac{1}{N} \left\langle {\mathcal{H}} \right\rangle,$$
(2)

where N is the total number of atoms belonging to the supercell unit. Our calculations are performed for a system size of N = 5 × 5 × 5.

The magnetizations are as follows:

$$M = \frac{1}{N} \left\langle {\sum\limits_{i} S_{i}} \right\rangle.$$
(3)

The magnetic susceptibilities are expressed as

$$\chi = \beta \left( {M^{2} - M^{2} } \right),$$
(4)

where T is the absolute temperature, β = 1/KBT, where kB is the Boltzmann constant fixed, in all this work, at its unit value kB = 1.

3 Results and discussion

In this section, we will provide the Monte Carlo simulations of the magnetic properties for both the structures (o-YMO) and (h-YMO) shown in Figs. 1 and 2, respectively. In fact, we start from the Hamiltonian given in Eq. (1) to investigate the different stable configurations of the manganite oxide perovskite YMnO3 in the absence of any temperature fluctuations (T = 0). From Eq. (1), the more stable configurations correspond to the minimum of the energies of the system. In a first step, the ground-state phase diagrams have been established in different planes of different physical parameters. Second, the results of Monte Carlo simulations are presented for non-null temperature values. Our results showed that the ground-state phase diagrams do not reveal a notable difference between the stable phases of the structures (o-YMO) and (h-YMO), while the Monte Carlo results revealed a notable difference between the behavior of the total magnetizations of the two structures: (o-YMO) and (h-YMO).

For the manganites, the stoichiometry is very important. Several studies show that the deviation of the concentration of the original cations, from a given value, can lead to a change in the charge state of the magnetic manganese cations. This can in turn greatly change the magnetic and electrical parameters of these compounds. The simplest statement is the deviation from oxygen stoichiometry, as it is the lightest ion. It is well known that the complex 3d-metal oxides easily allow the oxygen excess and/or deficit. Real samples are always poorly nonstoichiometric, especially in oxygen. Moreover, yttrium manganite with an orthorhombic structure is precisely obtained during synthesis in a reducing medium. On the other hand, after annealing in an oxygen environment, it becomes almost stoichiometric with the orthorhombic symmetry of the unit cell [64, 65].

The oxygen excess and deficit can increase and decrease the oxidation degree of 3d-metals. The changing of charge state of 3d-metals as a consequence of changing of oxygen content changes magnetic parameters such as total magnetic moment and Curie point. Moreover, oxygen vacancies affect exchange interactions. The intensity of exchange interactions decreases when the oxygen vacancy concentration increases. In the complex oxides, there is only indirect exchange. The exchange near the oxygen vacancies is negative according to Goodenough–Kanamori empirical rules. The oxygen vacancies should lead to the formation of a weak magnetic state such as spin glass. The question of separating the state of spin glass and cluster spin glass based on the field exponents remains highly relevant, see Refs. [66, 67]. To take into account the average crystallite size on the intensity of exchange interactions. Several experiences show that mass transport, and especially oxygen vacancy transport, destroys the grains [68, 69]. The average crystallite size on the intensity of exchange interactions is summarized in the expression of Hamiltonian given in Eq. (1). Our model takes into account an average of the number of oxygen atoms surrounding each Mn magnetic element.

When modeling the compound YMnO3, the only magnetic atoms are Mn3+ which are represented by the magnetic spin moment S = 2 (taking the values ± 1, ± 2 and 0). In reality, the chemical element Mn can be present either under the Mn2+ ion or the Mn3+ ion. In the present study, we are limited to the second ion element. The coexistence of the two Mn2+/Mn3+ ions can lead to a significant increase in the Curie temperature as a result of the effect of internal compression [70, 71].

3.1 Ground-state phase diagrams

In this part, a ground-state phase diagram interpretation is discussed for different physical parameter planes in Figs. 3 and 4, for the orthorhombic (o-YMO) and the hexagonal (o-YMO) structures of YMnO3, respectively. All stable possible phases 2S + 1=5 (with S = 2) are − 2, − 1, 0, 1 and 2.

Fig. 3
figure 3

Ground-state phase diagrams of orthorhombic YMnO3: a in the plane (H, Δ) for Jintra = 1 and Jinter = − 1; b in the plane (H, Jintra) for Jinter = − 1 and Δ = 0; c in the plane (H, Jinter) for Jintra = 1 and Δ = 0; d in the plane (Δ, Jintra) for Jinter = − 1 and H = 0; e in the plane (Δ, Jinter) for Jintra = 1 and H = 0; f in the plane (Jintra, Jinter) Δ = 0 and H = 0

Full size image
Fig. 4
figure 4

Ground-state phase diagrams of the hexagonal YMnO3: a in the plane (H, Δ) for Jintra = 1 and Jinter = − 1; b in the plane (H, Jintra) for Jinter = − 1 and Δ = 0; c in the plane (H, Jinter) for Jintra = 1 and Δ = 0; d in the plane (Δ, Jintra) for Jinter = − 1 and H = 0; e in the plane (Δ, Jinter) for Jintra = 1 and H = 0; f in the plane (Jintra, Jinter) Δ = 0 and H = 0

Full size image

In fact, Figs. 3a–f and 4a–f illustrate the ground-state phase diagrams in the planes (H, Δ), (H, Jintra), (H, Jinter), (Δ, Jintra), (Δ, Jinter) and (Jintra, Jinter), showing the stable configurations of the structures (o-YMO) and (h-YMO), respectively. Figures 3a and 4a reveal the obtained results in the planes (H, Δ) for Jintra = 1 and Jinter = − 1. All stable possible phases (− 2, − 1, 0, 1 and 2) are present in Figs. 3a and 4a with the same topology.

In the plane (H, Jintra), we provide the stable configurations of the two structures (o-YMO) and (h-YMO), for Jinter = − 1 and Δ = 0, in Figs. 3b and 4b, respectively. Except for the phases (− 1 and + 1) which have gained more space in the phase diagrams, the remaining ones (− 2, 0 and + 2) have not moved when comparing Figs. 3b and 4b.

After replacing Jintra by Jinter, Figs. 3c and 4c summarize the obtained results in the plane (H, Jinter) for Jintra = 1 and Δ = 0. Once again, the structures (o-YMO) and (h-YMO) do not show any significant difference concerning the five stable phases (− 2, − 1, 0, 1 and 2).

Figures 3d–f and 4d–f plotted in different planes (Δ, Jintra), (Δ, Jinter) and (Jintra, Jinter) illustrate the stable configurations for the two structures of the compound YMnO3. From these figures, it is found that only three phases (− 2, + 2 and 0) are stable in these planes. In fact, phase (0) is always found to be stable in the region where the parameters Δ, Jintra and Jinter are taking negative values, while the phases (− 2 and + 2) are stable in the region corresponding to positive values of the parameters Δ, Jintra and Jinter.

3.2 Monte Carlo results

In this section, we use Monte Carlo simulations to simulate the magnetic properties of the manganite oxide perovskite YMnO3. These calculations are performed using the Hamiltonian given in Eq. (1) with the free boundary conditions (nanosystem). During these simulations, we discard the first 104 generated configurations when performing 105 Monte Carlo steps. The Metropolis algorithm is used to reach the equilibrium of the system.

The results obtained by Monte Carlo simulations concerning the critical behavior of the two structures (o-YMO) and (h-YMO) are presented in Figs. 5a–d and 6a–d for Δ = 0, H = 0. In fact, Fig. 5a, c represents the profiles of the magnetizations of the structure (o-YMO) as a function of the temperature for Jinter = − 1 and different values of Jintra = 0.6, 0.8 and 1 (in Fig. 5a) and for Jintra = 1 and different values of Jinter = − 0.2, 0.2, 0.6 and 1 (in Fig. 5c). From these figures, it is found that when increasing the exchange coupling interaction values Jintra, the magnetization saturations increase. Concerning the susceptibility profiles of the structure (o-YMO), our results are summarized in Fig. 5b, d for Jinter = − 1 and for different values of Jintra = 0.6, 0.8 and 1 in Fig. 5b and for Jintra = 1 and different values of Jinter = − 0.2, 0.2, 0.6 and 1 in Fig. 5d, respectively. As it is expected, the peaks of the susceptibilities are displaced towards higher temperature values when increasing the exchange coupling interaction Jinter between different planes.

Fig. 5
figure 5

Profiles of the magnetizations and susceptibilities of (o-YMO) as a function of the temperature for Δ = 0, H = 0. a The magnetizations for Jinter = − 1 and different values of Jintra = 0.6, 0.8 and 1; b the susceptibilities for Jinter = − 1 and different values of Jintra = 0.6, 0.8 and 1; c the magnetizations for Jintra = 1 and different values of Jinter = − 0.2, 0.2, 0.6 and 1; d the susceptibilities for Jintra = 1 and different values of Jinter = − 0.2, 0.2, 0.6 and 1

Full size image
Fig. 6
figure 6

Profiles of the magnetizations and susceptibilities of (h-YMO) as a function of the temperature for Δ = 0, H = 0. a The magnetizations for Jinter = − 1 and different values of Jintra = 0.6, 0.8 and 1; b The susceptibilities for Jinter = − 1 and different values of Jintra = 0.6, 0.8 and 1; c The magnetizations for Jintra = 1 and different values of Jinter = − 0.2, 0.2, 0.6 and 1; d The susceptibilities for Jintra = 1 and different values of Jinter = − 0.2, 0.2, 0.6 and 1

Full size image

On the other hand, the profiles of the magnetizations of the structure (h-YMO) as a function of the temperature for Jinter = − 1 and different values of Jintra = 0.6, 0.8 and 1, and for Jintra = 1 and different values of Jinter = − 0.2, 0.2, 0.6 and 1, are presented in Fig. 6a, c. In accordance with Fig. 5a, c, these figures reproduce the fact that when increasing the exchange coupling interaction values Jintra, the magnetization saturations also increase. When exploring the behavior of the susceptibility profiles of the structure (h-YMO), our findings are illustrated in Fig. 6b, d for Jinter = − 1 and different values of Jintra = 0.6, 0.8 and 1 in Fig. 6b and for Jintra = 1 and different values of Jinter = − 0.2, 0.2, 0.6 and 1 in Fig. 6d. Once again, the peaks of the susceptibilities are moved towards higher temperature values when the exchange coupling interaction, Jinter, values, between different planes, increase.

The behavior of the hysteresis cycles of both the structures, (o-YMO) and (h-YMO), is provide in Figs. 7a, b and 8a, b, respectively. The increasing temperature effect, from T = 1 to T = 5, decreases the surface of the hysteresis cycles of (o-YMO) and (h-YMO) which is shown in Figs. 7a and 8a, respectively. The crystal field effect on the hysteresis loops of both structures is summarized in Figs. 7b (for Δ = − 5, 0 and 5) and 8b (for Δ = − 5, 0 and 3). From these figures, it is seen that the increasing crystal field effect is to increase the surface of the cycles. In the case of crystal field with positive values, these figures show the existence of steps corresponding to the intermediate states (since the spin moments are S = − 2, − 1, 0, 1, 2).

Fig. 7
figure 7

The hysteresis loops of o-YMnO3. a For fixed values of Δ = 0, Jintra = 1 and Jinter = − 1; and different values of temperature: T = 1, 3 and 5; b For fixed values of T = 1, Jintra = 1 and Jinter = − 1; and different values of the crystal field: Δ = − 5, 0 and 5

Full size image
Fig. 8
figure 8

The hysteresis loops of h-YMnO3. a For fixed values of Δ = 0, Jintra = 1 and Jinter = − 1; and different values of temperature: T = 1, 3 and 5; b for fixed values of T = 1, Jintra = 1 and Jinter = − 1; and different values of the crystal field: Δ = − 5, 0 and 3

Full size image

To inspect the increasing crystal field effect on the behavior of the magnetizations, we report in Figs. 9 and 10 the obtained results. In Figs. 9a and 10a, we display our results, for fixed values of T = 1, Jintra = 1 and Jinter = − 1, when varying different external field values H = 0.5, 1 and 2. The same topology is presented in Fig. 9a, for the structure (o-YMO) and in Fig. 10a, for the structure (h-YMO). The only difference is that, for the structure (h-YMO), the positive values of the crystal field do not affect the behavior of the magnetizations when varying the external magnetic field. The fact of varying the temperature is much more reflected in the region where the crystal field takes negative values, than in the region of its positive values, for the two structures: (o-YMO) and (h-YMO). It is also worth to note that the behavior of the magnetization is not affected by the temperature variations for positive values of the crystal field. The effect of varying the intra-plane exchange coupling interaction (Jintra = −  4, 1 and 4) is reflected in Figs. 9c and 10c for fixed values of T = 1, H = 0 and Jinter = − 1. It is found that for Jintra = − 4, the paramagnetic phase persists for the structure (o-YMO) despite increasing the crystal field. While, for the structure (h-YMO), except for the region (Δ < − 5), the paramagnetic phase disappears. When the intra-plane parameter takes the value Jintra = 1, the paramagnetic phase occurs for (Δ < − 2.5) for the structure (o-YMO), and for (Δ < − 2.0) for the structure (h-YMO). The magnetization reaches its saturation value (− 0.20) for both structures when increasing the crystal field towards positive values. For Jintra = + 4, the paramagnetic phase disappears rapidly in the structure (o-YMO) compared to the structure (h-YMO). A positive magnetization saturation value is reached for positive values of the crystal field.

Fig. 9
figure 9

Magnetization as a function of the crystal field for (o-YMO); a for different external field values H = 0.5, 1 and 2, and fixed values of T = 1, Jintra = 1 and Jinter = − 1; b for different temperature values T = 1, 3 and 5, and fixed values of H = 0, Jintra = 1 and Jinter = − 1; c for exchange coupling values Jintra = − 4, 1 and 4, and fixed values of T = 1, H = 0 and Jinter = − 1; d for exchange coupling values Jinter = − 4, − 1 and 4, and fixed values of T = 1, H = 0 and Jintra = 1

Full size image
Fig. 10
figure 10

The magnetization as a function of the crystal field for (h-YMO); a for different external field values H = 0.5, 1 and 2, and fixed values of T = 1, Jintra = 1 and Jinter = − 1; b for different temperature values T = 1, 3 and 5, and fixed values of H = 0, Jintra = 1 and Jinter = − 1; c for exchange coupling values Jintra = − 4, 1 and 4, and fixed values of T = 1, H = 0 and Jinter = − 1; d for exchange coupling values Jinter = − 4, − 1 and 4, and fixed values of T = 1, H = 0 and Jintra = 1

Full size image

To compare the effect of varying the crystal field on both the structures (o-YMO) and (h-YMO), we present in Figs. 9d and 10d the obtained results for fixed values of T = 1, H = 0 and Jintra = 1, and selected values of the exchange couplings Jinter = − 4, − 1 and 4, respectively. For Δ < − 5, the paramagnetic phase is persistent for the two structures. While, for Δ > − 5, the maximum saturation of the magnetization, with negative value, is reached only for the positive values of the exchange coupling interaction (Jinter = 4), see Figs. 9d and 10d.

In Figs. 11a–c and 12a–c, we report the effect of varying the intra-plane exchange coupling interactions on the behavior of the magnetization for the two structures of the compound YMnO3, in the absence of the external magnetic field (H = 0). The same topology is appearing in Figs. 11a and 12a, for fixed values of T = 1, and Jinter = − 1, for the two structures (o-YMO and h-YMO) when varying the crystal field Δ = − 5, 0 and 5. From these figures, it is found that for Δ = 0, the paramagnetic phase is always present despite varying the Jintra exchange coupling interaction. While the saturation magnetization (± 2) is reached for Δ = − 5, + 5, the saturation of the magnetization value follows the sign of the crystal field (− 2 for Δ = − 5 and + 2 for Δ = + 5). A transition of first order is appearing in the behavior of the total magnetizations when varying the parameter Jintra, as it is shown in Figs. 11b and 12b for fixed values of Δ = 0 and Jinter = − 1 and different temperature values T = 1, 3 and 5. The paramagnetic phase is found only in the (o-YMO) structure, while this phase is absent in the (h-YMO) structure for Jintra < 0. Also, the saturation of the magnetization is appearing only for high temperature values (T = 3 or 5).

Fig. 11
figure 11

Magnetization as a function of the exchange coupling Jintra for (o-YMO); a for different crystal field values Δ = − 5, 0 and 5, and fixed values of T = 1, H = 0, and Jinter = − 1; b for different temperature values T = 1, 3 and 5, and fixed values of H = 0, Δ = 0 and Jinter = − 1; c for exchange coupling values Jinter = − 4, − 1 and 4, and fixed values of T = 1, H = 0 and Δ = 0

Full size image
Fig. 12
figure 12

Magnetization as a function of the exchange coupling Jintra for (h-YMO); a for different crystal field values Δ = − 5, 0 and 5, and fixed values of T = 1, H = 0, and Jinter = − 1; b for different temperature values T = 1, 3 and 5, and fixed values of H = 0, Δ = 0 and Jinter = − 1; c for exchange coupling values Jinter = − 4, − 1 and 4, and fixed values of T = 1, H = 0 and Δ = 0

Full size image

To complete this study, we provide in Figs. 11c and 12c the obtained results when varying the parameter Jinter on the behavior of the magnetization for fixed values of T = 1 and Δ = 0 and selected values of the exchange coupling values Jinter = − 4, − 1 and 4. The paramagnetic phase is appearing for Jintra < 0 in the (o-YMO) structure for all values of Jinter (see Fig. 11c), while this phase is present only for Jinter = − 4 in the (h-YMO) structure. On the other hand, the effect of varying the parameter Jinter is important in the region Jintra > 0, but this effect is negligible for the positive values of Jintra, for the both structures (o-YMO and h-YMO), see Figs. 11c and 12c.

To complete the study of the behavior of the total magnetizations of the alloy YMnO3, when varying different physical parameters, we illustrate in Figs. 13a–c and 14a–c the obtained results, when varying Jinter in the absence of the external magnetic field. In fact, we present in Figs. 13a and 14a the obtained results when varying the crystal field on the behavior of the magnetization for fixed values of T = 1 and Jintra = 1 and selected values of the crystal field Δ = − 5, 0 and 5. The paramagnetic phase is appearing for Jinter < 0 in the two structures (o-YMO) and (h-YMO) only for Δ = 0 (see Figs. 13a, 14a). While, for Δ = − 5 or 5, the saturation of the magnetization is appearing for positive values of Jinter, respecting the sign of the crystal field (the saturation is positive for Δ = + 5 and negative for Δ = − 5).

Fig. 13
figure 13

The magnetization of the compound YMnO3 as a function of the exchange coupling Jinter for the structure (o-YMO) for H = 0; a for different crystal field values Δ = − 5, 0 and 5, and fixed values of T = 1 and Jintra = 1; b for different temperature values T = 1, 3 and 5, and fixed values of Δ = 0 and Jintra = 1; c for the exchange coupling values Jintra = − 4, 1 and 4, and fixed values of T = 1 and Δ = 0

Full size image
Fig. 14
figure 14

The magnetization of the compound YMnO3 as a function of the exchange coupling Jinter for the structure (h-YMO) for H = 0; a for different crystal field values Δ = − 5, 0 and 5, and fixed values of T = 1 and Jintra = 1; b for different temperature values T = 1, 3 and 5, and fixed values of Δ = 0 and Jintra = 1; c for the exchange coupling values Jintra = − 4, 1 and 4, and fixed values of T = 1 and Δ = 0

Full size image

The effect of varying the temperature on the behavior of the magnetizations is reported in Figs. 13b and 14b, for fixed values of Δ = 0 and Jintra = 1 and for selected temperature values T = 1, 3 and 5. The paramagnetic phase is appearing only for the structure (o-YMO) for Jinter < − 2, while this phase is not stable for the structure (h-YMO). On the other hand, the saturation of the magnetizations reached for positive values of the parameter Jinter. Moreover, for the structure (o-YMO) the saturation value of the magnetization is positive for low temperature (T = 1) and negative for higher temperature values (T = 3 or 5). This situation is inverted for the structure (h-YMO), only for the temperatures T = 1 and 3.

The magnetization behavior of the compound YMnO3 as a function of the exchange coupling Jinter for the two structures (o-YMO) and (h-YMO) is plotted in Figs. 13c and 14c for the exchange coupling values Jintra = −  4, 1 and 4, and fixed values of T = 1 and Δ = 0. From these figures, it is found that the paramagnetic is omnipresent for Jintra = −  4 in the two structures (o-YMO) and (h-YMO). The saturation of the magnetization is reached in the structure (o-YMO) for Jintra = 1 and 4 with the positive value (+ 2). While, for the structure (h-YMO), the only reached saturation magnetization value (− 2) is found for the value Jintra = 1.

4 Conclusion

In this work, we have studied the magnetic properties of the yttrium manganite oxide YMnO3 which can crystallize in either the hexagonal (h-YMO) or orthorhombic (o-YMO) structure. These two structures are studied using Monte Carlo simulations under the Metropolis algorithm. The ground-state phase diagrams are studied and discussed in different planes corresponding to different physical parameters. On the other hand, we examine and discuss the critical behavior and the dependency of the magnetizations and the susceptibilities as a function of the temperature, the crystal field, the exchange coupling interactions and the external magnetic field.

To complete this study, we have illustrated the behavior of the magnetizations as a function of the exchange coupling interactions to show and understand the behavior of the magnetizations as a function of other physical parameters. In addition, we have investigated and discussed the effect of varying the exchange coupling interactions on the total magnetizations, for fixed temperature values. Moreover, we have provided and analyzed the hysteresis cycles of the studied manganite oxide perovskite YMnO3 compound as a function of the external magnetic field, for specific values of the crystal field, the exchange coupling interactions and the temperature.