1 Introduction

High-quality micro-structuring of thin metallic films by ultrashort pulsed laser radiation, e.g., no debris, no burr and no damage of the substrate, is of increasing interest for thin film electronics, like organic electronics [3]. In order to describe the removal process consistently, the dependences of the ablation on the laser radiation parameters, e.g., pulse duration, pulse energy, fluence or wavelength, as well as material parameters, like density, reflectivity, heat capacity or heat conductivity, have to be investigated completely. This understanding of ultrashort laser ablation and the change in morphology is also important for the process modeling used in optical metrology, like the ellipsometry, to extract the complex refractive index of the investigated matter being irradiated by laser radiation.

This article is subdivided in five sections. The first section describes the experimental setup and the measurement techniques for determining the experimental data. The next section introduces some theoretical and modeling background. Subsequent, the results for single pulse ablation of thin aluminum films are presented with respect to the obtained ablation regimes as well as the dependency of the ablation threshold on the film thickness. These studies are completed by the results of multi-pulse irradiation, and finally the results are summarized and a short outlook to further work is given.

2 Experimental setup and measurement

The laser radiation, provided by a femtosecond laser system (Pharos, Light Conversion Ltd., λ = 1028 nm, \({\tau _{\mathrm{H}}}\) = 200 fs, \(M^2\) = 1.2), is guided by high-reflecting dielectric mirrors to the focusing setup. An internal Pockels-cell allows to deliver single pulses, or pulse bursts with defined number of pulses at defined pulse repetition rate, here f p = 1 MHz. The laser radiation is positioned on the target surface by a X–Y-galvanometer scanner (intelliSCANde, Scanlab AG) mounted on a motorized linear stage, and is focused on the target surface (\(d_\sigma \) = 30 µm) using a f-\(\varTheta \)-objective (f = 167 mm). The investigated aluminum films were deposited by sputtering on float glass. The roughness of the surface and the crystallinity were not measured. For sake of simplicity, the thermo-physical and optical properties are assumed to be the properties of bulk aluminum. The surface topology of the ablation structures was investigated by optical microscopy (Nikon Labophot-2 in transmission and reflection mode) and by confocal microscopy (Confovis GmbH).

3 Fundamentals and modeling

The laser radiation reaching the surface of a material is partially reflected or transmitted according to the Fresnel equations [4] and afterward absorbed within the material by the electron system depending on the absorption coefficient. Thereby, the electron system is excited into a non-equilibrium state [5]. The electrons collide with each other and transfer energy. After a defined time, called relaxation time \(\tau _{\mathrm{rel}}\), a thermal equilibrium within the electron system is reached and the energy distribution of the electron system can be described by a Fermi distribution. Assuming that these relaxation time \(\tau _{{\rm rel}}\) is small compared to the pulse duration \(\tau _{\mathrm{H}}\), the energy transfer between the electron and the phonon systems can be described by the two-temperature model (TTM) proposed by [6] and expanded by many authors like [5, 7]. The heat conduction equation for the electron system is given by

$$\begin{aligned} C_{\mathrm{e}_{V}} (T_\mathrm{e} )\cdot \frac{\partial T_\mathrm{e}}{\partial t}= & \nabla \cdot \left( \lambda _{\mathrm{th}_\mathrm{e}} (T_\mathrm{e},T_{\mathrm{ph}} )\cdot \nabla T_\mathrm{e} \right) \\ \nonumber- & G(T_\mathrm{e})\cdot (T_\mathrm{e}-T_{\mathrm{ph}} )+q_{V} (\mathbf {r},t), \end{aligned}$$
(1)

and the heat conduction equation for the phonon system by

$$\begin{aligned} C_{\mathrm{ph}_{V}}\cdot \frac{\partial T_{\mathrm{ph}}}{\partial t}=G(T_\mathrm{e} )\cdot (T_\mathrm{e} - T_{\mathrm{ph}} ). \end{aligned}$$
(2)

The volumetric heat capacity of the electrons \( C_{\mathrm{e}_{V}} (T_\mathrm{e} )\) and the coupling factor \(G(T_\mathrm{e} )\) were taken from [8]. The thermal conductivity of the electrons \(\lambda _{\mathrm{th}_\mathrm{e}}\) is described by the Drude model according to

$$\begin{aligned} \lambda _{\mathrm{th}_\mathrm{e}} (T_\mathrm{e},T_{\mathrm{ph}} )=\frac{1}{3}\cdot v_{\mathrm{F}}^2\cdot C_{\mathrm{e}_{V}} (T_\mathrm{e} )\cdot \tau _\mathrm{e}(T_\mathrm{e},T_{\mathrm{ph}} ). \end{aligned}$$
(3)

\(v_{\mathrm{F}}\) represents the Fermi velocity and is assumed to be constant. \(q_{V}\) represents the volumetric heat source, and \(\tau _\mathrm{e}\) the relaxation time of the electrons, which is the time among two impacts between two electron or one electron and one phonon. The volumetric heat source is given by

$$\begin{aligned} q_{V} (\mathbf {r},t)= & I_0\cdot \left( \frac{w_0}{w(z_{\mathrm{S}}-z_0 )} \right) ^2 \cdot \alpha (z_{\mathrm{S}} )\nonumber \\&\quad \cdot (1-R(z_{\mathrm{S}} ))\cdot \mathrm {e}^{-\int _{z_{\mathrm{S}}}^z \alpha (r,z) \mathrm{d}\zeta }\nonumber \\&\quad \cdot \mathrm {e}^{-2\cdot \frac{r^2}{w^2 (z_{\mathrm{S}}-z_0 ) }}\cdot \mathrm {sech}^2\left( 1.763 \cdot \frac{t-t_0}{\tau _\mathrm{H}}\right) . \end{aligned}$$
(4)

\(z_{\mathrm{S}}=z_{\mathrm{S}} (r)\) represents the position of the surface depending on the lateral position, \(I_0\) the maximum intensity at the waist position \(z_0\) given by \( I_0=\frac{2\cdot Q}{{\uppi }\cdot w_0^2\cdot 1.1344\cdot \tau _{\mathrm{H}} }\), \(w_0\) the waist radius at \(z_0\), w the beam radius at z S, R(z S) the reflectivity on the surface, t 0 the maximum peak time, Q the pulse energy and \(\alpha \) the absorption coefficient. \(\alpha \) can be expanded to include the range of ballistic electrons as described by [5], but in our formula the absorption coefficient is only described by the complex refractive index. For the simulations, the initial position of the surface is equal to the position of the beam waist and is set to zero, so \(z_0=z_{\mathrm{S}}= 0\). If vaporization occurs, z S changes. An expansion of the material due to heating is neglected. All following calculations are related to aluminum. The relaxation time \(\tau _\mathrm{e}\) can be calculated by [9, 10]

$$\begin{aligned} \frac{1}{\tau _\mathrm{e}} =A_\mathrm{e}\cdot T_\mathrm{e}^2+B_{\mathrm{ph}}\cdot T_{\mathrm{ph}}. \end{aligned}$$
(5)

The Parameter \(A_\mathrm{e}\) was derived from [10] to \(0.376 \cdot 10^7 \frac{1}{\mathrm{s}\cdot \mathrm{K}^{2}}\) and the commonly used value for the parameter B ph is \(3.9 \cdot 10^{11} \mathrm{s}^{-1}\mathrm{K}^{-1}\) [10]. As a new proposal, now the parameter B ph will be directly coupled to the experimental data. Assuming that the temperature of the electron system equals to the temperature of the phonon system, \(\tau _\mathrm{e}\) is only determined by the phonon system \(\frac{1}{\tau _\mathrm{e}} \approx B_{\mathrm{ph}}\cdot T_{\mathrm{ph}}\). This relaxation time is also used in the Drude model calculating the relative permittivity for intraband processes \({\tilde{\varepsilon }}_{\mathrm{r, intra}}\) [2, 11]

$$\begin{aligned} {\tilde{\varepsilon }}_{(\mathrm{r, intra})}= & 1-\frac{\sigma _0\cdot \tau _\mathrm{e}}{\varepsilon _0\cdot (1+\omega ^2\cdot \tau _\mathrm{e}^2 )}-\mathrm {i}\cdot \frac{\sigma _0\cdot \tau _\mathrm{e}}{\varepsilon _0\cdot \omega \cdot (1+\omega ^2\cdot \tau _\mathrm{e}^2 ) } \end{aligned}$$
(6)

where \(\sigma _0\) represents the dc conductivity, \(\varepsilon _0\) the vacuum permittivity, and \(\omega \) the frequency of the laser radiation. Equation (6) is also often written in terms of the plasma-frequency \(\omega _{\mathrm{p}}=\frac{n_\mathrm{e}\cdot e^2}{\varepsilon _0\cdot m_\mathrm{e}}\), e.g., in [11, 12]. These formulas are equal and can be converted into each other. The relaxation time can also be determined by

$$\begin{aligned} \tau _\mathrm{e} (T)=\frac{\sigma _0 (T)\cdot m^*}{e^2\cdot n_\mathrm{e} (T) }, \end{aligned}$$
(7)

where e represents the elementary charge, \(n_\mathrm{e}\) the density of conduction electrons, and m* the effective mass of the electrons [2]. Here, to include effects of the lattice potential, the effective mass is used instead of the classical electron mass. All parameters on the right side of Eq. (7), except e, are temperature dependent. The parameters \(\sigma _0 (T)\) for the solid and liquid state of aluminum are derived from [13]. For the solid state, m* can be obtained comparing the experimental and theoretical value of the Sommerfeld-parameter \(\gamma \) and is tabulated in [14]. The value of m* for the liquid state was taken from [2]. The density of the conduction electrons \(n_\mathrm{e}\) can be derived by the change of density \(\rho (T)\) [15] according to

$$\begin{aligned} n_\mathrm{e} (T)=v\cdot \frac{\rho (T)}{m_\mathrm{A} }, \end{aligned}$$
(8)

where v represents the number of valence electrons and \(m_A\) the atomic mass. Under equilibrium conditions the relaxation time is only determined by the phonon system, and one can combine Eqs. (5), (7) and (8) to

$$\begin{aligned} B_{\mathrm{ph}} (T_{\mathrm{ph}} )=\frac{e^2}{\sigma _0 (T_{\mathrm{ph}} )\cdot m^* \cdot T_{\mathrm{ph}}} \cdot v\cdot \frac{\rho (T_{\mathrm{ph}}) }{m_\mathrm{A}} . \end{aligned}$$
(9)

Another method for calculating B ph is based on the measured temperature-dependent values of the thermal conductivity \(\lambda _{\mathrm{th_0}} (T)\). The necessary values are derived from [16]. The values for \(\lambda _{\mathrm{th_0}} (T)\) include the contribution of the electron (\(\lambda _{\mathrm{th}_\mathrm{e}}\)) and phonon (\(\lambda _{\mathrm{th}_{\mathrm{ph}} }\)) system. Assuming again equal temperatures of both systems, the thermal conductivity is purely determined by the electron system [17], \(\lambda _{\mathrm{th}_\mathrm{e}} \gg \lambda _{\mathrm{th}_{\mathrm{ph}}} \), but depending on the phonon temperature. Applying Eqs. (3) and (5) for a thermal equilibrium gets

$$\begin{aligned} B_{\mathrm{ph}} (T_{\mathrm{ph}} )=\frac{v_\mathrm{F}^2\cdot C_{\mathrm{e}_\mathrm{V}} (T_{\mathrm{ph}})}{3\cdot \lambda _{\mathrm{th}_0} (T_{\mathrm{ph}})\cdot T_{\mathrm{ph}})}. \end{aligned}$$
(10)

The comparison between the commonly used value for \(B_{\mathrm{ph}}\) in literature and the value derived with Eqs. (9) and (10) are visualized in Fig. 1. Applying the average of Eqs. (9) and (10) at room temperature results in the value used in literature and was also confirmed for the metals gold, silver and copper. Therefore, the average is used for the following calculations.

Fig. 1
figure 1

Dependence of the parameter \(B_{\mathrm{ph}}\) on the phonon temperature in comparison with the used value in literature (dashed line)

Full size image

The finally resulting thermal conductivity of the electrons \(\lambda _{\mathrm{th}_\mathrm{e} }\), according to Eq. (3) and including Eqs. (5), (9) and (10), are depicted in Fig. 2 for different temperatures of the electron and phonon system.

Fig. 2
figure 2

Dependence of the thermal conductivity of the electrons on the electron temperature for four different phonon temperatures in comparison with the thermal conductivity of aluminum at room temperature (dashed line)

Full size image

Vice versa, Eq. (5) leads for different temperatures of the electron and phonon system to a temperature-dependent permittivity \({\tilde{\varepsilon }}_\mathrm{r} (T_\mathrm{e},T_{\mathrm{ph}})\). This approach is an extension of a proposed model by [2] considering the temperature dependence of reflectivity using Eq. (7). Instead of Eqs. (7),  (5) can be used with the average of Eqs. (9) and (10). The total permittivity includes also the interband effects, which can be described by the Lorentz model

$$\begin{aligned} {\tilde{\varepsilon }}_\mathrm{r}= & {} {\tilde{\varepsilon }}_{\mathrm{r,intra}}+{\tilde{\varepsilon }}_{\mathrm{r,inter}},\nonumber \\ {\tilde{\varepsilon }}_\mathrm{r}= & {} {\tilde{\varepsilon }}_{\mathrm{r,intra}}+\sum _{j=1}^N \frac{f_{ j}\cdot \omega _\mathrm{p}^2}{\omega _{ j}^2-\omega ^2+\mathrm {i}\cdot \varGamma _{ j}\cdot \omega }. \end{aligned}$$
(11)

\(f_\mathrm{j}\) represents the weight of the j-th oscillator with the frequency \(\omega _{ j}\), and \(\varGamma _{ j}\) the damping constant, where \(\tau _{ j}=1/\varGamma _{ j}\) represents the lifetime [11]. The complex permittivity refers to the refractive index by

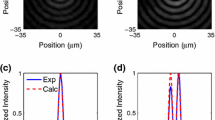
$$\begin{aligned} \tilde{n} =\sqrt{\tilde{\varepsilon }_\mathrm{r}}=n -\mathrm {i}\cdot \kappa . \end{aligned}$$
(12)

All parameters of the interband contributions are also temperature dependent, but the only known dependency is again given by the density of conduction electrons, Eq. (8), in \(\omega _{\mathrm{p}}\). The other parameters are set constant. As all parameters in the Lorentz model, including the intraband contribution \(\tilde{\varepsilon }_{\mathrm{r,intra}}\), are fitted to experimental data [11], the fit has to be repeated and set the intraband contribution \(\tilde{\varepsilon }_{\mathrm{r,intra}}\) to constant. The final result of n and \(\kappa \) can be seen in Fig. 3. The approximated function fits well to the experimental data for small wavelength, but has a difference for larger wavelengths beginning at about 1 µm. This difference is used as a constant offset in all simulations. It should be noted that the effects of the temperature-dependent interband contribution are small compared to the temperature-dependent intraband part.

Fig. 3
figure 3

Comparison of the experimental data of n and \(\kappa \) [10] to the fit of the Lorentz model as a function of the wavelength

Full size image

Based on the calculated complex refractive index, the reflectivity R for perpendicular incidence [4] and for the transition air to metal, is given as function of electron temperature for different phonon temperatures (Fig. 4).

Fig. 4
figure 4

Dependence of the reflectivity on the electron temperature for four different phonon temperatures

Full size image

All simulations are performed for two-dimensional axial symmetry. Equations (1) and (2) are discretized by Finite Differences and solved by a convolution of the temperature distribution and a convolution kernel for the derivatives, as it is state of the art in digital image processing. The numerical change of the phase state is based on a formula used by [18] considering the latent heat of fusion \({\Delta }H_M\) and of vaporization \({\Delta }H_V\) in the volumetric heat capacity of the phonons.

$$\begin{aligned} C_{\mathrm{ph}_{ V}}= & \rho (T_{\mathrm{ph}} )\cdot \Bigg [c_{p_0}+\Bigg .\frac{{\Delta }H_\mathrm{M}}{\mathrm{{\Delta }} T\cdot \sqrt{2\cdot {\uppi }}}\cdot \mathrm {e}^{-\frac{1}{2}\cdot \left( \frac{T_{\mathrm{ph}}-T_\mathrm{M}}{\mathrm{{\Delta }} T}\right) ^2} \nonumber\\ &\quad +\Bigg .\frac{\mathrm{{\Delta }} H_\mathrm{V}}{\mathrm{{\Delta }} T\cdot \sqrt{2\cdot {\uppi }}} \cdot \mathrm {e}^{-\frac{1}{2}\left( \frac{T_{\mathrm{ph}}-T_\mathrm{V}}{\mathrm{{\Delta }} T}\right) ^2}\Bigg ]. \end{aligned}$$
(13)

\(c_{\mathrm{p}_0}\) represents the heat capacity calculated by the Debye model [14] and set to be constant. The parameter \({\Delta }T\) determines the width of the zone of phase change and should be 20 K up to 50 K. \(T_\mathrm{M}\) and \(T_\mathrm{V}\) are the melting and vaporization temperature, respectively. If the phonon temperature of a pixel rises \(T_\mathrm{M}+{\Delta }T/2\), it is considered as melted. Similar, if the phonon temperature of a pixel rises \(T_\mathrm{V}+{\Delta }T/2\), it is considered as vaporized, and excluded from the simulations.

One example, describing heating a 300 nm thick aluminum film irradiating it by three different pulse energies using the experimental parameters, as well as all described fundamentals, is visualized in Fig. 5.

Fig. 5
figure 5

Simulation results for three different pulse energies; solid lines maximum electron temperature \(T_\mathrm{e}\); dashed lines maximum phonon temperature \(T_{\mathrm{ph}}\); points: temporal power distribution in a.u.; peak power at t 0 = 600 fs

Full size image

The reflectivity decreases during irradiation leading to increased absorbed energy and higher electron temperatures (Fig. 5). Increasing the pulse energy decreases the time to reach a minimum reflectivity given by the absorbed energy and increases the reached maximum phonon temperature. Therefore, for higher pule energies, more energy is absorbed during the laser pulse. In contrast to the simulations, higher pulse energies in the experiment lead not necessarily to more ablated volume, because some limiting processes, like interaction of the laser radiation with the ablated particles and the evolution of a plasma, occur. A jump in reflectivity during the phase transition from liquid to vapor can also be identified. Larger pulse energies lead to higher electron temperatures, and the relaxation time \(\tau _{\mathrm{R}}\) to reach a thermal equilibrium between the electron and phonon system, increases too. This is in agreement to the theory as the relaxation time \(\tau _{\mathrm{R}}=C_{\mathrm{e}_\mathrm{V}}/G\) increases with higher electron temperatures for aluminum [8]. Furthermore, the phonon temperature increases faster for higher pulse energies compared to lower pulse energies justified by the high temperature difference \(T_\mathrm{e}-T_{\mathrm{ph}}\).

4 Single-pulse ablation

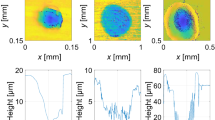
Several thin films of aluminum were irradiated by focused femtosecond laser radiation. Three different topologies of the resulting structures were observed (Fig. 6). For a film thickness of d = 300 nm, an outer (gentle ablation) and an inner diameter (strong ablation) of the ablation structure was formed by the laser radiation. Plotting the measured ablation depth \(z_A\) by confocal microscopy as function of the peak fluence \(H_0=\frac{2\cdot Q}{{\uppi }\cdot w^2}\) two regimes can be distinguished by the different obtained ablation depths (Fig. 7). For thin films, like d = 100 nm, just one topology is visible representing an overlap of both regimes. For thin films with a thickness between 100 and 300 nm, a differentiation between the two regimes can be detected. Films with a thickness of 150 nm represent a transition regime, because the separation begins and no clear differentiation is possible. Therefore, the outer structures are assigned to the gentle ablation and the inner diameter to the strong ablation.

Fig. 6
figure 6

Ablation structures for three different film thicknesses irradiated with the same pulse energy of \(Q=7\,\upmu \) J; blue float glass substrate; detected by optical microscopy, \(D_S\)-diameter strong ablation, \(D_G\)-diameter gentle ablation

Full size image
Fig. 7
figure 7

Single-pulse ablation depths \(z_A\) as a function of the fluence; d = 300 nm; detected by confocal microscopy, fit to guide the eye

Full size image

For a film thickness of 300 nm and using low peak fluences up to \(2.2\;\hbox {J}/\hbox {cm}^{2}\), only gentle ablation occurs and a small increase in the ablation depth \(z_A\) can be detected for increasing fluence (Fig. 7). Beginning from a peak fluence of \(2.2\;\hbox {J}/\hbox {cm}^{2}\) the regime for strong ablation can be detected and an ablation depth independent of the peak fluence for gentle ablation is measured. In the strong ablation regime, the metal film is completely removed. An analytical description of the ablation depth for the two ablation regimes as a function of the fluence can be found in [7, 19] predicting a logarithmic dependency of the ablation depth on the fluence for gentle ablation and a linear dependency for strong ablation. This is in contrast to other authors, like [20, 21], applying a logarithmic dependency for strong ablation, too. Nevertheless, all of these formulas are not applicable for our experiments, because our film thicknesses are too small and the complete film is ablated with one pulse. Therefore, for strong ablation, no linear or logarithmic dependency on the fluence can be stated. Furthermore, the threshold for occurring of strong ablation can not be explained by the formulas used by [20, 21].

Recasts of melting could be observed on the border of the ablation structures, like ejections and ring-like structures (Fig. 6), indicating an explosion process of molten material often discussed in literature, such as coulomb explosion for gentle ablation [22], and phase explosion [22, 23] as well as critical-point phase separation [24] for strong ablation. Furthermore, the results support the model proposed by [25] of forming bumps and jets or droplets. The numerical investigations of [26] identifies thermal stress caused by ultrafast heating and melting as the driving mechanism for forming bumps, but the authors only concentrated on irradiating the thin film from the glass substrate back side.

The diameters D of the ablation structures were measured by optical microscopy, and in a first step the squared diameter, for the strong and gentle regime, over the log pulse energy was applied for determination of the beam radius w and the threshold pulse energy \(Q_{\mathrm{thr}}\). Based on the results, the threshold fluence \(H_{\mathrm{thr}}=\frac{2\cdot Q_{\mathrm{thr}}}{{\uppi }\cdot w^2 }\) can be derived. In the second step the diameter squared over log peak fluence \(H_0\) is performed (Fig. 8). The determined beam radius w of the gentle ablation measurements is also used for strong ablation, as the same laser beam creates both ablation structures.

Fig. 8
figure 8

Squared diameter over log peak fluence for different thin film thicknesses of aluminum

Full size image

The derived thresholds fluences are summarized in Fig. 9 and compared with the simulated thresholds at the same laser parameters.

Fig. 9
figure 9

Experimentally and by simulation derived thresholds of gentle and strong ablation in dependence of the layer thickness, all lines to guide the eye

Full size image

For thin layers d < 100 nm, smaller thresholds due to heat accumulation (Fig. 10) were obtained experimentally and by simulation. The reason is just a 2D heat diffusion to surrounding areas instead of a 3D diffusion. It can also be observed that the separation in gentle and strong ablation regime, beginning from just one regime, starts at 100-nm film thickness. For strong ablation an approximately linear dependency on the film thickness was detected, whereas the gentle ablation regime converges against an upper limit for bulk material [6]. The error bars for strong ablation and d = 300 nm are very large due to less data points and high fluctuations of the detected diameters; therefore, a logarithmic dependency of the ablation threshold on the film thickness, as for gentle ablation, cannot be excluded. A linear dependency of the ablation threshold on the film thickness for removing thin aluminum films with a single pulse was reported by [28] corresponding to our experiments on strong ablation. In contrast to our determined thresholds, the authors of [28] reported much larger fluences using a different measurement technique for threshold determination, detecting the LIBS-signal (laser induced breakdown spectroscopy) of the substrate. A qualitative agreement of the simulated melting thresholds with the experimental ablation thresholds for gentle ablation let us assume a non-thermal explosion as the dominating ablation process for this ablation regime (Fig. 9). Numerical investigations of [29, 30] describing lifting of a small liquid layer up from the surface, although no vaporization occurs, supports our assumption. In contrast, an agreement of the simulated threshold for vaporization to strong ablation is not possible. Nevertheless, the simulated results show the need of including a temperature-dependent reflectivity, because without, no vaporization can be derived.

The simulations depict clearly a higher phonon temperature for smaller film thicknesses due to heat accumulation (Fig. 10 bottom). In contrast to thin films, where the film is nearly homogeneously heated, the bottom end of the film for d = 300 nm remains cold. Furthermore, the highest electron temperature for very small film thicknesses d = 50 nm is reached, and the time for reaching the thermal equilibrium between electron and phonon system last longest, since heat accumulation takes also in the electron system place. Due to higher temperatures at the same pulse energy, the ablation threshold for thin films gets smaller than for thicker ones. This trend is also confirmed for d = 50 nm as melting occurs (\(T_{\mathrm{ph}}>T_\mathrm{M}\); \(T_\mathrm{M}= 933\) K) and the other films stay in the solid state.

Fig. 10
figure 10

Simulated temperature distribution for four different film thicknesses of aluminum by irradiating with a single pulse (\(Q=\) 1 µJ); Top Temperature as function of time, maximum electron temperature (solid lines), maximum phonon temperature (dashed lines); Bottom Phonon temperature as function of normalized film thickness (dashed lines) at \(t= 5\) ps compared with room temperature (dotted line)

Full size image

5 Multi-pulse ablation

A distinct separation between gentle and strong ablation was only clearly observed for the film thickness d = 300 nm. Thus, only the ablation thresholds for d = 300 nm are presented (Fig. 11). The applied fluence is only based on the fluence of the single pulse and not on the sum of the pulse energy of all pulses.

Fig. 11
figure 11

Dependence of the experimentally derived thresholds for gentle and strong ablation on the number of pulses per point for a layer thickness d = 300 nm; Fit for calculation of incubation parameter S

Full size image

An increasing number of pulses per point leads to a reducing of the thresholds. This dependence of the threshold can be led back on an incubation effect described by the incubation model of Jee [1]

$$\begin{aligned} H_{\mathrm{thr}} (N_\mathrm{p} )=H_{\mathrm{thr}} (1)\cdot N_\mathrm{p}^{\mathrm{S}-1}, \end{aligned}$$
(14)

with the fitting parameters \(S_{\mathrm{gentle}}= 0.606\) and \({S_{\mathrm{strong}}= 0.336}\).

For these experiments, no comparison simulations were performed for the large pulse separation time of 1 µs, given by the setup, leading to very long computation times. Therefore, some theoretical simulations for double pulses with a variable pulse separation time from 1 up to 300 ps were performed for a layer thickness of 100–300 nm (Fig. 12). The results for the double pulses are compared with a single pulse having the same pulse energy as the sum of the pulse energy of the two double pulses. Also, the threshold fluence is calculated by the sum of the pulse energy.

Fig. 12
figure 12

Simulated thresholds for melting and vaporization as a function of the pulse separation time compared with a single pulse (separation time zero)

Full size image

A minimum of the thresholds for melting and vaporization at about 5–10 ps is observed (Fig. 12) resulting from a minimum of the reflectivity at this time. This time represents nearly the relaxation time \(\tau _\mathrm{R}\). For longer separation times, the diffusion of heat to the surrounding areas lead to smaller electron and phonon temperatures and the reflectivity increases. Furthermore, for shorter separation times, the phonon temperature reaches its maximum and according to Fig. 4 the reflectivity reaches its minimum. A distinct minimum of the threshold fluence for vaporization is determined for d = 300  nm. For d = 100 nm the thresholds for melting and vaporization converge against a limit smaller than the thresholds for single pulses resulting from the heat accumulation. Therefore, the thresholds for d = 100 nm are also smaller than the thresholds for d = 300 nm. No comparable results for aluminum were found in literature as mostly only the ablation depth is the subject of investigations [31, 32].

6 Summary and outlook

The thresholds for single-pulse ablation were determined by applying the squared diameter over log peak fluence. Two ablation regimes, the gentle and the strong ablation, were classified for layer thicknesses d > 100 nm. For smaller film thicknesses just one ablation regime could be determined. As a result, smaller thresholds were obtained by reducing the layer thickness due to heat accumulation. The threshold for strong ablations features a linear dependence on the film thickness. For further investigations to this dependency, experiments with thicker films and higher fluences are necessary. A qualitative agreement between the experiments for single pulses and the irradiation in the gentle ablation regime with the simulated melting thresholds could be achieved. Recasts of melting could be detected around the ablation structures of the two ablation regimes indicating explosive processes, such as coulomb, phase explosion, critical-point phase separation or thermal stress due to ultrafast heating as the dominant ablation processes.

The simulation can not discriminate the two experimentally observed ablations regimes. So, further models have to contain other ablation mechanisms, like phase explosions. To predict the observed ablation structures, a coupling with beam propagation is also necessary.

An increasing number of pulses per point led to a reducing of the thresholds described by incubation model of Jee. Due to the long computation times for a pulse separation time of \(1\,\upmu \) s, theoretical investigations performed for double pulses with a separation time between 1 and 300 ps describe a minimum for the thresholds of melting and vaporization at about 5–10 ps.